探求解析几何中动点横(纵)坐标取值范围(最值)的策略

武增明

(云南省玉溪第一中学 653100)

平面解析几何中动点横(纵)坐标取值范围(最值)问题，是高考中的热点，是教师教学中的重点，是同学学习中的难点.由于这类问题，没有固定的解题模型，没有规律可循，解法灵活，思维性强.因此，大多数同学想不到、找不到解题的切入点与突破口，心生畏惧，一筹莫展.对此问题，笔者试想，没有定法，应该有法，应该有策略.有几种？具体是什么方法？是什么策略？笔者结合自己多年积累的教学资料(教师错题集)和教学经验，反复思考，反复探究，归纳总结，给出如下六种策略，希望对同学们的学习有所启示和帮助，希望对同仁的教学有参考价值.

一、走数形结合之路

虽然解析几何是用代数方法研究几何学问题的学科，但是仍然离不开由数想形、由数画形、以形助数、由形化数，问题获解.

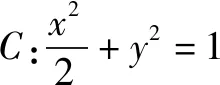
图1

二、走三角函数之路

选取变量角为自变量，建立所求与变量角的函数关系式，把问题转化为三角函数的值域(最值)问题，问题获解.

例2 (2014年高考全国卷Ⅱ理科数学第16题)设点M(x0，1)，若在圆O：x2+y2=1上存在点N，使得∠OMN=45°，则x0的取值范围是____.

分析选取∠MNO为自变量，记∠MNO=α，应用正弦定理建立x0与α的关系式，问题转化为求角α的三角函数的值域问题.

解因为点M(x0，1)在直线y=1上运动，记∠MNO=α，如图2，则∠MON+α=135°，所以0°<α<135°，又因为MO≥ON，所以在△MON中知，α≥45°，于是45°≤α<135°.

图2

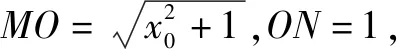
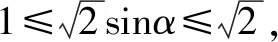
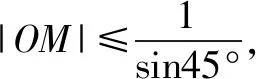
图3

三、走数量积定义之路

根据数量积定义，进行向量坐标运算，建立关于所求的不等式，问题获解.

四、走代数函数之路

选取动直线的变量斜率k或变量横截距a或变量纵截距b或圆锥曲线中的参变量为自变量，建立所求与变量斜率k或变量横截距a或变量纵截距b或圆锥曲线中的参变量的函数关系式，把问题转化为代数函数的值域(最值)问题，问题获解.

解 方法1由题意可设直线AB的方程为y=kx+1，A(x1，y1)，B(x2，y2).

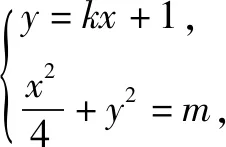
因为P(0，1)，所以由AP=2PB，得-x1=2x2， ③

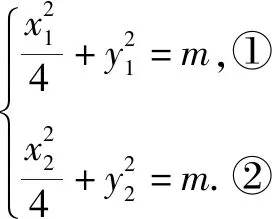
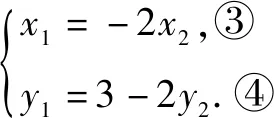
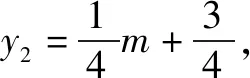
五、走判别式之路

依题意，选取一个参变量，建立所求与所选取的参变量的关系式，由此得关于以参变量为未知数的一元二次方程，根据一元二次方程有实根的充要条件是判别式不小于零，问题获解.

例5 已知抛物线y=x2上有一定点A(-1，1)和两动点P，Q，当PA⊥PQ时，点Q的横坐标取值范围是____.

六、走圆锥曲线范围之路

建立所求与圆锥曲线上动点横(纵)坐标的关系式，再利用圆锥曲线范围，问题获解.