基于Dixon优化算法的双频匹配网络设计

王龙岗， 陈章友， 吴雄斌， 王 欢

(武汉大学电子信息学院， 武汉 430072)

高频地波雷达(high frequency surface wave radar,HFSWR)工作在短波(3～30 MHz)波段，利用垂直极化的电磁波沿海洋表面绕射传播的特性，能够克服地球曲率的限制，实现对海上目标和海态的超视距、全天候探测，具有探测成本低、范围广、实时性好等特点[1]，成为海洋探测的重要手段。而其发射天线的物理尺寸较大是限制HFSWR推广应用的重要因素，随着技术的发展，HFSWR对发射天线的多频化工作和小型化的要求越来越迫切[1-3]，而由此造成的阻抗不匹配也成为该技术发展中不可避免的问题[4-6]。由于HFSWR对于发射效率要求较高，要使小型化后的双频/多频天线能够满足工程要求，必须设计相应的双频/多频匹配网络。

阻抗匹配作为天线和微波/射频电路设计的一个基本任务，一直受到中外学者广泛关注和研究。利用实频分析设计匹配网络的方法，后来被不断改进并广泛用于宽带匹配的设计[7]。近年来，许多学者针对微波/射频段的匹配网络进行了大量研究，如利用两段传输线设计而成双频匹配网络[8]，在双频匹配网络的基础上扩展而成的三频匹配网络[9]等，这些研究成果主要是基于分布元件的，为微波/射频电路的设计提供了有利帮助，但这些方法不适用于短波波段的匹配电路设计。而利用集总元件设计匹配电路的研究相对比较少，Nallam等[10]提出了一种利用集总元件进行多频段匹配网络设计的方法，但是这种方法基于频率变换的解析法，不适用于结构复杂的电路；Rodriguez等[11]利用实数编码的遗传算法设计高频天线的匹配网络，虽然能够实现宽带设计，但是算法的计算过程比较复杂；Li等[2]利用集总元件构成的陷波器实现天线的双频功能，但是这种方法有比较大的局限性，调节比较困难，而且天线结构较复杂；任仪等[12]利用非福斯特匹配网络匹配接收天线，这种利用有源器件进行匹配网络设计比较复杂，且不适用于HFSWR大功率发射天线。黄晓丹[4]通过在天线谐振频点f0两侧各设置一个谐振频率为f1、f2串联谐振电路，利用谐振电路的特性实现了对电小天线的匹配，但是该方法设计的匹配网络复杂，不适用于双频匹配。

针对上述问题，提出了利用Dixon优化算法设计匹配网络的方法。该方法首先根据待匹配的对象，选择一种合适的、结构简单的拓扑结构，然后根据拓扑结构中各元件之间的串并联关系以及负载的阻抗推导出匹配网络输入端的阻抗表达式，该表达式包含各元件参数，再利用网络输入端的阻抗构造优化算法的目标函数，并把各元件的参数作为优化变量，最后利用Dixon算法得到各元件参数的值，并对仿真与实测结果进行了分析。

1 双频匹配网络及其输入阻抗

通过串联电感并联电容或者串联电容并联电感，可以使某个特定频点对应的输入阻抗沿着Smith圆图的等电阻或等电导圆移动，实现单频匹配。多频匹配网络可以借鉴单频匹配网络的思想，将多个单频匹配网络并联，通过选择合适的元件值，可以实现多频匹配。选择的匹配网络的拓扑结构如图1所示。匹配网络由并联的两支路组成，元件Z1和元件Y1组成匹配网络的上支路，元件Z2和元件Y2组成匹配网络的下支路。元件Z1、元件Y1、元件Z2和元件Y2既可以是电感元件也可以是电容元件，而且元件Z1和元件Y1、元件Z2和元件Y2可以交换位置，可等效为L型、Π型和T型网络。由于上下支路之间会有耦合作用，因此分析网络输入阻抗时要将整个匹配电路作为一个二端口网络整体考虑。

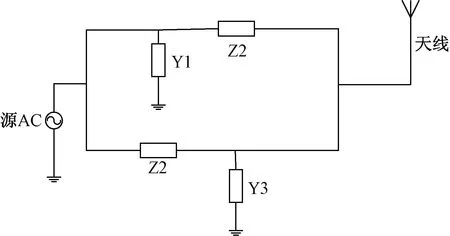
图1 匹配网络的拓扑结构Fig.1 Topological structure of matching network

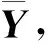
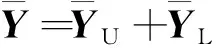
(1)

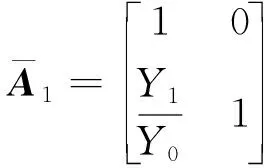
(2)

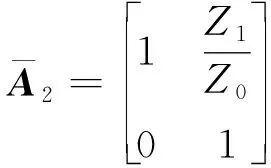
(3)

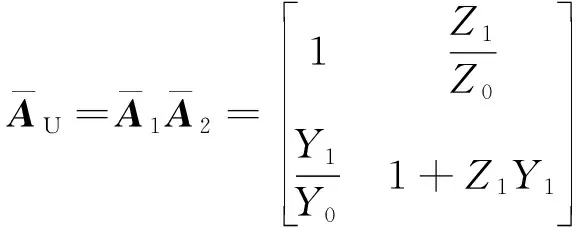
(4)

(5)

根据A矩阵与Y矩阵之间的转换关系，可以得到整个匹配网络的归一化A矩阵为

(6)

匹配网络的输入阻抗Zin以及反射系数Γin可分别表示为

(7)

(8)

式中：a、b、c、d为A矩阵的参数；Z0为传输线的特征阻抗；ZL为天线的输入阻抗，代入式(7)可以计算网络输入端的阻抗Zin。

要实现阻抗匹配，则要求匹配网络的输入阻抗Zin与传输线的特征阻抗Z0要近似相等，即要求反射系数Γin要尽可能小。而Zin与天线输入阻抗以及各元件的参数是相关的，因此反射系数Γin与各元件的取值是相关的。考虑到在实际应用中，电容元件具有较大的寄生电阻，损耗较大，在设计匹配网络时，电感元件尽量采用串联形式，电容元件尽量采用并联形式。

在双频或多频匹配网络的优化问题中，以网络中各元件的参量作为优化变量，以匹配网络输入端的反射系数作为目标函数，由于双频匹配网络要在两个频点都需要满足匹配要求，对应的会有两个目标函数，因此可以通过加权将两个或多个目标函数合成一个目标函数。可以表示为

f(x1,x2,…xN,f1,f2,…fM)=

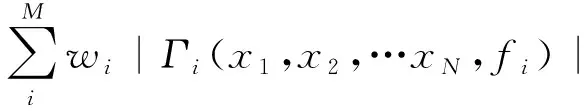
(9)

式(9)中：xj为第j个网络元件参数(j=1,2,…,N)，其中N为网络中元件的数目；fi为需要匹配的第i个频率点(i=1，2，…，M)；M为待匹配的频点数；wi为第i个频率点权重；Γi为第i个频率点的反射系数。

通过优化算法计算出在给定拓扑结构情况下，使式(9)达到最小时的网络中各元件的值，即可得到对应该拓扑结构的最优网络。

2 利用Dixon优化算法求解元件参数

目前常用的优化算法众多，如遗传算法[11]、梯度下降算法等，而对于目标函数表达式比较复杂，求导不容易的实际问题，这些算法计算过程比较复杂，而Dixon算法[13]提供了一种比较简洁的思想。

Dixon算法是数值优化算法中的直接法，通过构建一个二次函数：

(10)

式(10)中：x为n维变量；H为二次项系数；b为一次项系数；c为常数项。

使二次函数Q(x)与目标函数f(x)在控制点上的值相等来实现对目标函数的逼近，从而以二次函数Q(x)的极小点作为f(x)的近似极小点，然后再改变控制点找到f(x)更好的二次近似函数Q(x)以改善极小值点的位置，从而构成迭代[14]。在计算过程中只用到函数f(x)的值，适合目标函数表达式复杂或没有表达式的情况。

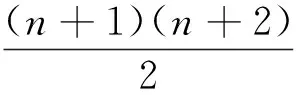
Dixon算法步骤如下。

步骤1随机生成(n+1)个初始点xi，i=0,1,2,…,n。

步骤2计算各点的函数值fi=f(xi)，i=0,1,2,…,n。

步骤3对xi重新排序，使得fi≤fi+1，i=0,1,2,…,n-1。

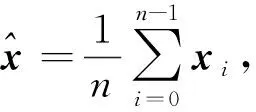
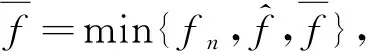
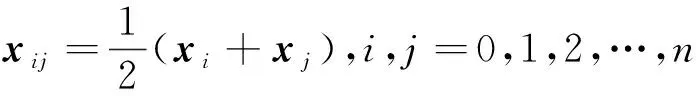
步骤9求出第n+2个点的函数值fn+1=f(xn+1)，若fn+1>fn则方法失败，若xn+1=xn方法也失败，停止计算，否则用xn+1替换xn，转到步骤3进行新的循环。

按照上述步骤不断进行循环迭代，直到算法失败或者满足收敛条件即找到能够使得二次函数较好逼近目标函数。

在实验中所用传输线的特征阻抗Z0为50 Ω，对于高低两个频率，ZL分别为(21.5+15.8i) Ω、(44.3+12.9i) Ω，代入式(7)可以得到匹配网络输入端阻抗，进而得到只含有未知元件参数的目标函数，利用优化算法进行优化。图1所示的拓扑结构中，各元件的初始化参数为：Z1为900 nH的电感，Y1为500 pF的电容、Z2为700 nH的电感、Y2为800 pF的电容。将其作为第一个点的4个参数值，并以此为基础随机生成其余4个点。利用Dixon优化算法经过约460次迭代得到的各元件的参数：Z1为2 874 nH的电感，Y1为655 pF的电容、Z2为 1 655 nH 的电感、Y2为800 pF的电容。由于上下支路的两个电感元件之间是并联关系，将其等效为一个电感元件1 050 nH，可以减小元件带来的损耗，而匹配网络的效果不会受到影响，该拓扑结构也简化为一个Π型网络，如图2所示。

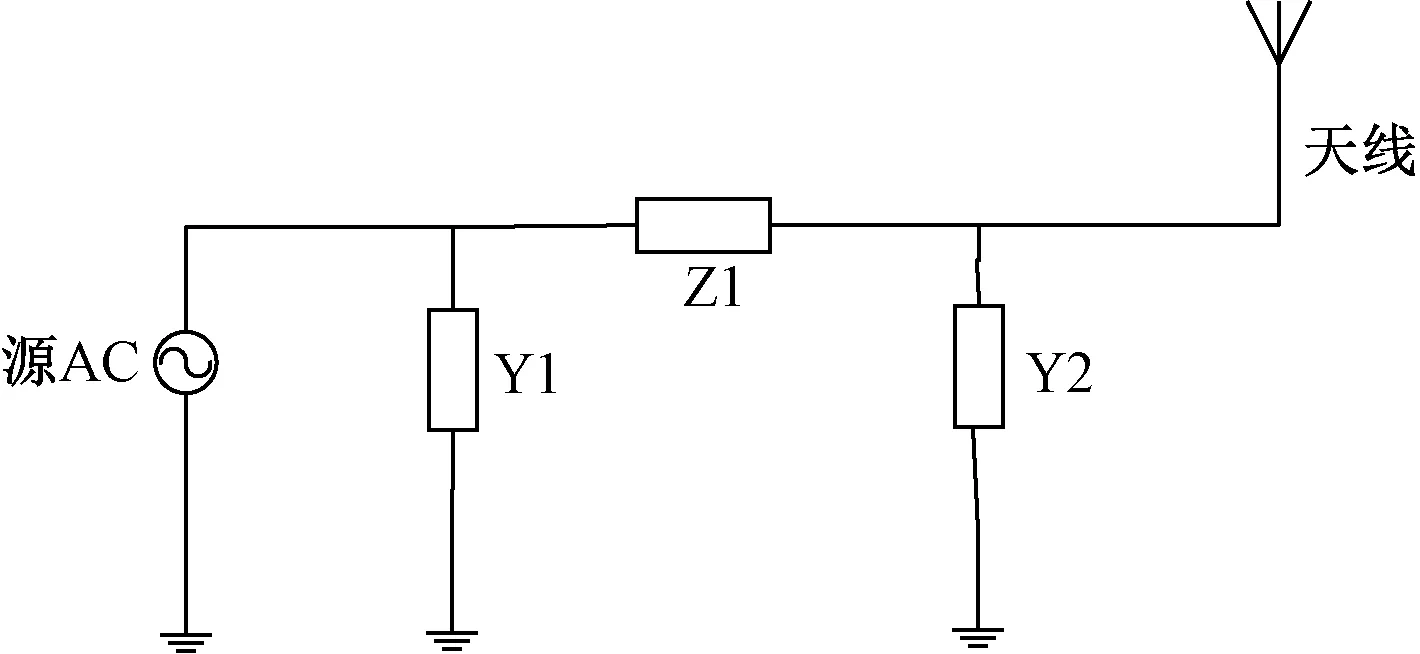
图2 双频匹配网络等效拓扑结构Fig.2 Equivalent topology of dual frequency matching network

能够同时工作在多频点的雷达在探测性能与抗干扰能力方面表现出明显优势，成为未来雷达的发展方向。因此将小型化双频天线扩展为三频天线，以便雷达能够同时工作在多个频点上。为了保证三频天线能正常工作，对双频匹配网络也进行扩展使其成为三频匹配网络。对于3个频率，ZL分别为(19.9+17.7i) Ω、(32.5+10.9i) Ω、(35.2+9.7i) Ω，利用Dixon优化算法进行求解各元件值时，依然借助前面对网络输入阻抗的推导，并且构造式(9)形式的目标函数。根据优化算法求解得到的各元件值，进行元件的等效替代后，最终得到图3所示的拓扑结构。其中，Z2为1 868 nH的电感元件，Y2为174 pF的电容元件，Z3为1 662 pF的电容元件，Y3为1 785 nH的电感元件。

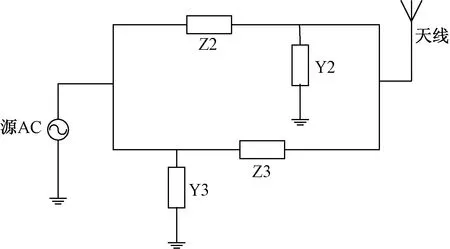
图3 三频匹配网络等效拓扑结构Fig.3 Equivalent topology of triple frequency matching network

3 匹配网络的仿真及实测结果分析

3.1 双频匹配仿真结果分析

为了验证利用优化算法得到的各元件参数值的有效性，根据优化的结果，在软件ADS中设计相应的匹配电路，进行仿真计算，得到的仿真结果如图4所示。可以看出，未加入匹配电路之前，中心频率4.2 MHz附近的低频谐振点反射损耗较大，不能直接使用；中心频率7 MHz附近的高频谐振点阻抗特性稍好，但是中心频率有偏移。加入利用优化算法设计的匹配电路后，低频谐振点的阻抗特性得到了明显改善，匹配效果良好，高频谐振点的带宽特性也到了改善。以驻波比小于2计算，低频谐振点带宽有80 kHz，高频谐振点的带宽达到200 kHz以上，能够满足设计要求。

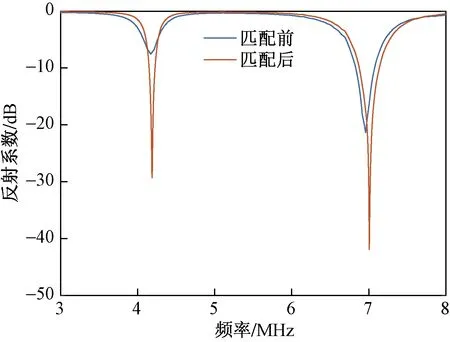
图4 双频匹配前后的对比(仿真)Fig.4 Comparison without and with dual frequency matching network (simulation)

3.2 三频匹配仿真结果分析

根据利用Dixon优化得到的三频匹配网络中各元件的参数，在ADS中设计相应的匹配电路，得到的仿真结果如图5所示。可以看出，加入匹配电路前，由于反射损耗过大，天线不能直接工作在4.2 MHz 附近，加入匹配电路后，天线的阻抗特性得到了明显的改善。尤其是4.2 MHz附近的低频谐振点，能够实现良好匹配。对于7 MHz以及11 MHz附近的谐振点，中心谐振频率更接近所要求的频率，而且匹配程度更好。对于各谐振点，驻波比小于2的带宽均大于60 kHz， 在11 MHz附近带宽甚至达到800 kHz，完全能够满足实验要求。利用本文提出的方法，将双频匹配网络扩展为三频匹配网络，依然能够具有良好的匹配效果。

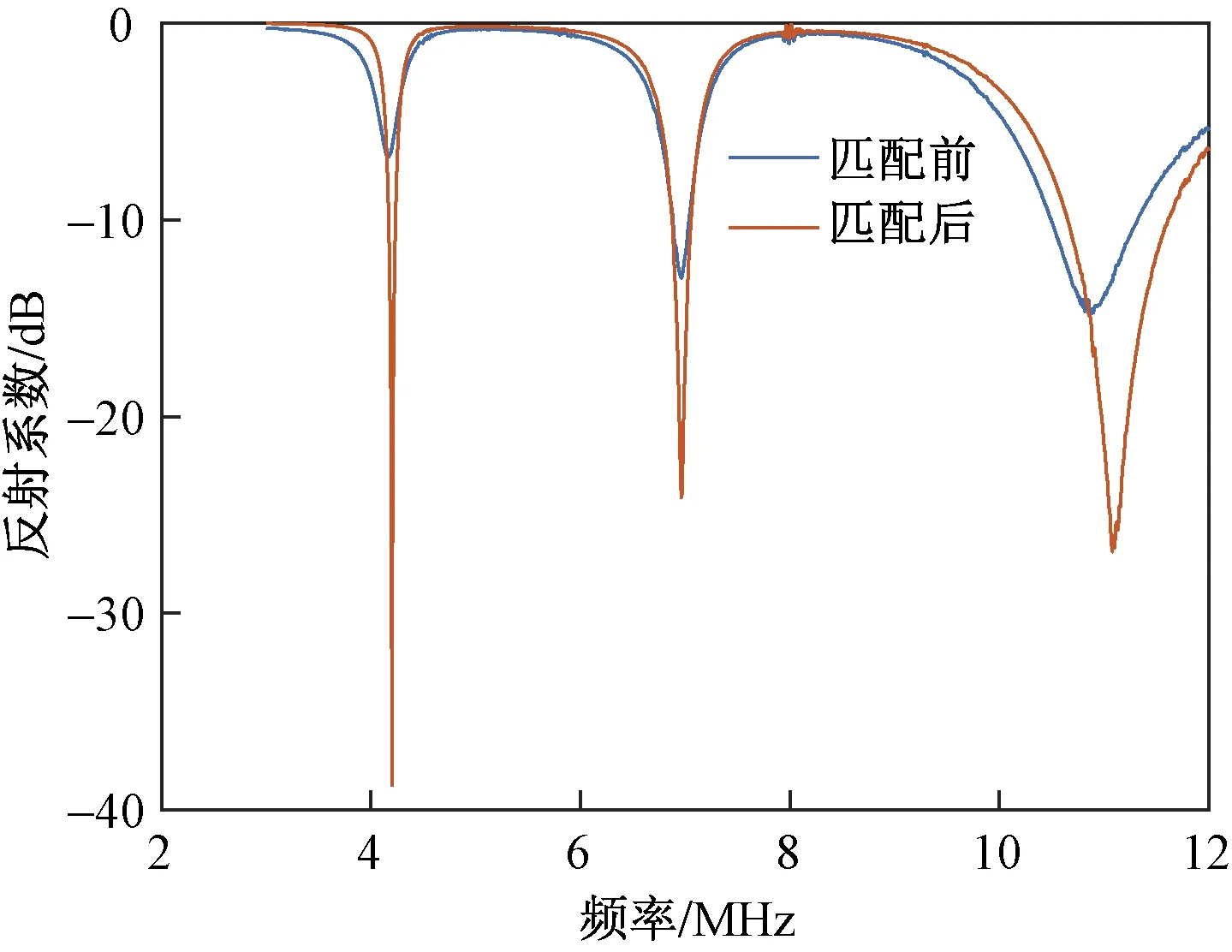
图5 三频匹配前后的对比(仿真)Fig.5 Comparison without and with triple frequency matching network (simulation)

3.3 双频匹配实测结果分析

利用优化算法得到的值虽然能够得到比较好的仿真效果，但是在实际工程应用中，这些值对应的单个元件可能难以获得，因此需要根据现有的元件对取值进行微调。图2中Y1选择680 pF的电容，Z1选择1 050 nH的电感，Y2选择820 pF的电容。在实验中测得的天线的数据如图6所示。

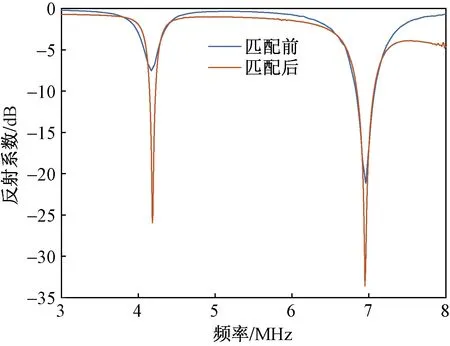
图6 双频匹配前后的对比(实测)Fig.6 Comparison without and with dual frequency matching network (measured)

可以看出，加入匹配电路后，天线的阻抗特性得到了很大改善，反射系数大幅缩小。以驻波比小于2计算带宽，天线在高低两个频点处的带宽分别是75 kHz和210 kHz，能够满足设计要求。将所设计的匹配网络应用在设计的小型化双频天线上，可同时得到如图7所示的实测海洋回波(Rang-Doppler谱，距离谱)。可以看出，频率为7 MHz时，雷达的距离探测范围超过150 km，频率为4.2 MHz时，雷达的距离探测范围超过 250 km。这些实测结果说明了在外场探测过程中天线是可以正常工作的，同时也说明所设计的匹配网络是能够发挥应有作用的，该研究具有工程价值和实际意义。

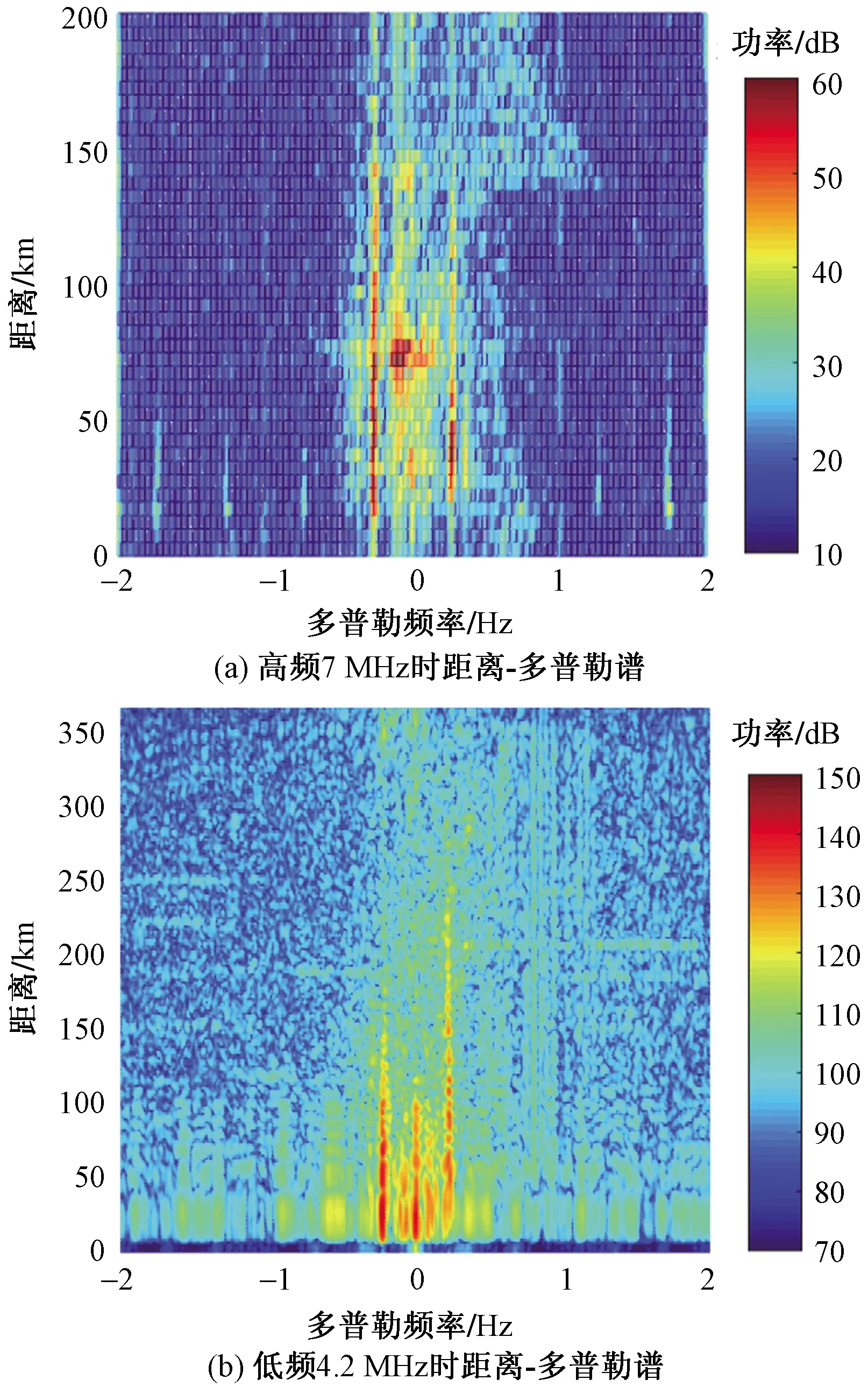
图7 实测的海洋回波谱Fig.7 Measured ocean echo spectrum

虽然天线谐振点的频率有偏移，但是偏移量不大，依然在所要求的带宽范围内，不影响天线的正常使用。造成偏差的原因主要是元器件标称值的不准确，耐高压电容元件标称值与实际值之间存在较大误差；电感元件采用漆包线自制，其测量值也存在较大误差；而且元件都不是理想元件，会存在寄生电阻，优化得到的值实际单个元件无法获得，这些因素都会引起误差，因此实测与仿真之间存在误差是正常现象。

4 结论

在单频匹配网络的基础上，设计了一款结构简单的双频匹配网络。在对网络的输入阻抗进行分析时，考虑了双频匹配网络各元件之间的耦合作用，基于所设计的匹配网络的拓扑结构，推导出了输入阻抗与匹配网络中各元件参数之间的关系，并用其构造了优化算法的目标函数。引入Dixon算法对网络中元件参数进行了优化，最终得到了能够同时满足双频匹配的匹配网络，仿真和实验结果均表明，该匹配网络能够满足在各谐振点处带宽大于 60 kHz的设计要求，而且所用元件较少，匹配网络带来的损耗很小。对双频匹配网络进行扩展，得到了能够同时谐振在3个频点的三频匹配网络，仿真结果表明，该匹配网络在各谐振点的带宽也能满足在各谐振点带宽大于60 kHz的设计要求，说明了本文方法用于设计多频匹配网络的可行性和有效性，能够满足工程实际需要。