基于混沌精英黏菌算法的无刷直流电机转速控制

肖亚宁， 孙 雪， 李三平， 姚金言

(东北林业大学机电工程学院， 哈尔滨 150040)

无刷直流电机(brushless direct current motor, BLDCM)由于结构简单、可靠性高且机械性能良好，而被广泛应用于航空航天、国防军事、机器人等领域[1-2]。在BLDCM转速控制中最常用的方法是传统比例-积分-微分(proportional integral differential，PID)控制[3]，但BLDCM是一种非线性、强耦合的复杂系统[4]，传统PID控制品质对比例、积分和微分3个控制参数依赖性强，很难适应不同的工作条件，因此控制时往往会出现转速调节精度不高、响应速度慢、抗干扰能力差等问题，无法达到理想的控制效果[5]。

近年来，随着人工智能和计算机科学的蓬勃兴盛，出现了大量基于自然现象启发的群智能优化算法，例如：蜻蜓算法(dragonfly algorithm, DA)[6]、灰狼优化算法(grey wolf optimizer, GWO)[7]、鲸鱼优化算法(whale optimization algorithm, WOA)[8]、饥饿游戏搜索算法(hunger games search, HGS)[9]等。这些智能算法原理简单、易于实现，能够有效解决各种复杂问题，因此越来越多学者尝试利用其对BLDCM转速PID控制器进行优化设计，以进一步控制精度和工作稳定性。文献[10]提出了一种利用粒子群算法在线自整定PID控制方法，使得无刷直流电机具有更好的动态响应性能，但因算法本身搜索能力不足而在迭代后期易于陷入局部最优；文献[11]采用改进遗传算法优化无刷直流电机模糊PID控制器，可以降低稳态误差，提高响应速度，但因遗传算法复杂的选择，交叉，变异过程导致参数整定效率低下，转速控制精度有待提高；文献[12]提出了一种基于飞蛾火焰优化算法的模糊控制器设计方法，但因算法参数较多，且根据经验选取的模糊规则、隶属度函数具有很大程度上的主观性，难以达到理想的控制性能。

黏菌算法(slime mould algorithm, SMA)是一种全新的群智能仿生算法[13]，相比其他算法具有更加优秀的搜索性能，已在不同领域得到一定程度的应用。Nguyen等[14]利用SMA算法优化梯级水电站设计；Zubaidi等[15]提出了一种SMA算法混合人工神经网络模型用于城市用水需求量的预测；Kumar等[16]成功利用SMA算法对太阳能光伏电池模型进行参数辨识。然而标准SMA算法依然面临着初始种群质量低，探索和开发过程难以平衡，迭代后期易于陷入局部最优等问题的困扰，收敛速度和求解精度仍有很大的提升空间。

因此，为弥补传统控制方法在BLDCM转速调节中的局限性，进一步增强标准SMA算法的全局搜索能力，提出了一种整合Tent混沌映射和精英反向学习策略的改进黏菌算法，并将其用于优化BLDCM速度环PID控制器，实现参数在线自整定。仿真和实验结果表明基于改进黏菌算法优化后的BLDCM转速控制系统具有响应速度快，抗干扰能力强，搜索效率高等优点。

1 BLDCM数学模型

无刷直流电机采用三相星形连接，其等效电路如图1所示。

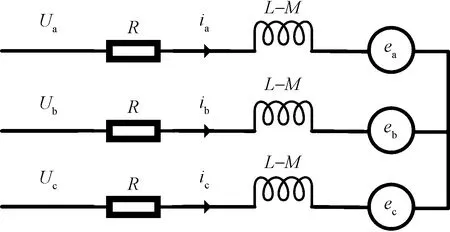
图1 无刷直流电机等效电路Fig.1 Equivalent circuit of BLDCM

无刷直流电机由定子和转子组成，通过控制其定子绕组上的电流频率及波形，可以改变转子的运行状态。为了方便分析，假定电机定子绕组完全对称，空间上互差120°电角度，忽略磁路饱和，不计涡流和磁滞损耗，不考虑齿槽效应，电枢绕组均匀连续分布在定子内表面，得到无刷直流电机的三相定子电压平衡方程为[17]

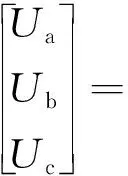
(1)

式(1)中：Ua、Ub、Uc分别为三相绕组相电压；R为三相绕组相电阻；ia、ib、ic分别为三相相电流；L为定子相绕组自感；M为定子相绕组互感；d/dt为微分算子；ea、eb、ec分别为三相反电动势。

电机运行时，任意时刻的电磁功率P为三相绕组电磁功率之和，故电机的电磁转矩方程为

P=eaia+ebib+ecic

(2)

(3)

式(3)中：Te为电机电磁转矩；ω为旋转角速度。

无刷直流电机的运动方程为

(4)

式(4)中：TL为负载转矩；B为阻尼系数；J为电机转动惯量。

2 标准黏菌算法

SMA是由Li等[13]于2020年提出的一种新型元启发算法，其主要模拟了自然界中黏菌觅食过程中的行为和形态变化。与其他智能优化算法相比，黏菌算法具有原理简单、调节参数少、寻优能力强、便于实现等优点。黏菌是一种生活在潮湿寒冷环境中的真核生物，其营养的摄取主要来源于外界有机物。当黏菌接近食物源时，生物振荡器将通过静脉产生一个传播波，以增加细胞质流量。食物浓度越高，生物振荡器产生的传播波也就越强，则细胞质流动越快，通过数学模型模拟上述逼近行为。

(5)

p=tanh|S(i)-DF|

(6)

参数a的计算公式为

(7)

式(7)中：t为当前迭代次数；tmax为最大迭代次数。

黏菌的质量系数W模拟了黏菌在不同食物浓度下的振荡频率，这有助于黏菌在找到高质量食物时能够更快地接近食物，从而提高搜索效率，其表达式为

(8)

Index=sort(S)

(9)

式中：bF和wF分别为当前迭代过程中获得的最优、最差适应度；Index为适应度序列；r为区间[0,1]上的随机值，用于模拟黏菌静脉收缩模式的不确定性；condition表示S(i)排序中前1/2的种群。

3 混沌精英黏菌算法

3.1 混沌初始化

研究表明，初始种群的多样性有助于提高算法的收敛速度和准确性，SMA算法通常采用随机数法初始化种群，在解决复杂优化问题时，存在后期种群多样性降低，易于陷入局部最优等缺陷[18]。目前文献中大多运用Logistic混沌映射优化智能算法产生混沌序列，丰富种群多样性。但相较于Logistic混沌映射，Tent混沌映射更加结构简单，收敛速度快，具有更好的遍历均匀性。设置种群规模为500，分别采用两种方法在区间[0,1]范围内产生混沌序列，其空间分布直方图如图2所示。可以看出，Logistic混沌映射生成的序列在区间[0,0.1]和[0.9,1]范围内的概率要高于其他各段，而Tent混沌序列在可行域内分布相对均匀。因此采用Tent混沌映射在SMA算法迭代初期进行种群初始化，使得个体位置均匀分布在搜索空间内，有助于提高算法求解效率。Tent混沌映射的数学表达式为

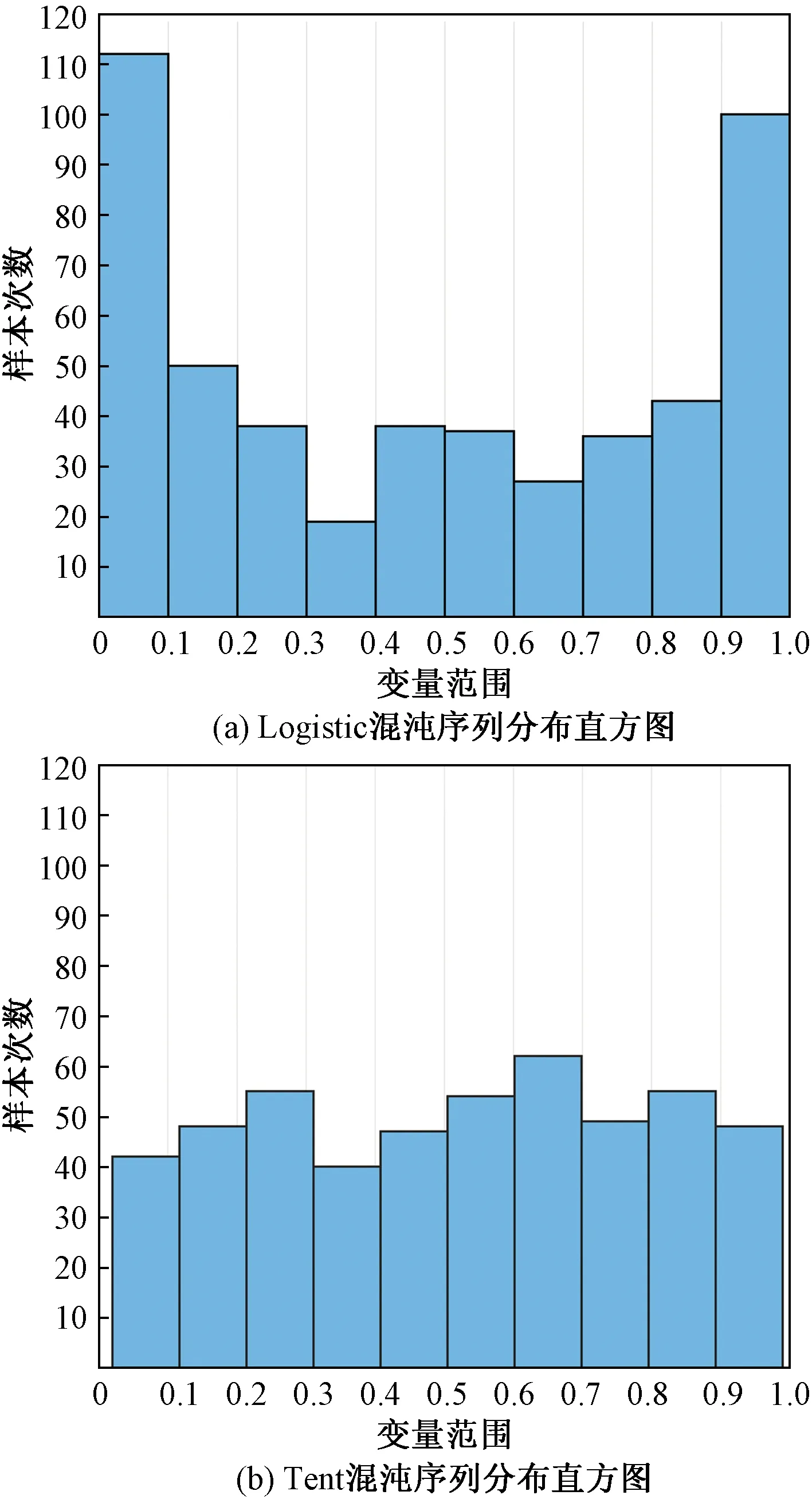
图2 Logistic与Tent混沌映射分布对比Fig.2 Comparison of Logistic and Tent chaotic mapping distribution

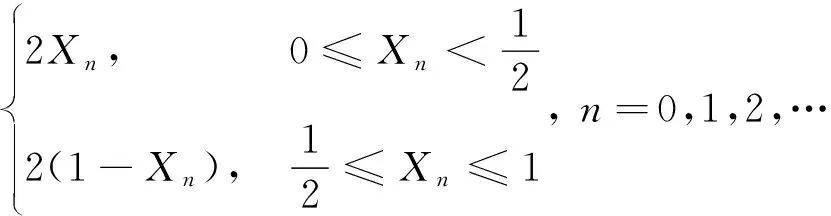
(10)

式(10)中：n表示映射次数；Xn表示第n次映射函数值。

采用Tent混沌映射生成初始种群的步骤如下。

步骤1 在[0,1]内随机生成初始值的初值X0[X0应避免落入小周期(0.2，0.4，0.6，0.8)]进入标志组，且S(1)=X0，i=j=1。

步骤2 利用式(10)进行迭代，产生新变量Xi，i=i+1。

步骤3 如果迭代达到最大次数，执行步骤5；若生成的X落入小周期点，则转到步骤3；若未出现上述现象，执行步骤2。

步骤4 令Xi=S(j+1)=S(j)+ε，j=j+1，其中ε为随机数,执行步骤2。

步骤5 程序运行停止，保存产生的混沌序列。

3.2 精英反向学习策略

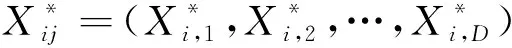
(11)

式(11)中：Xi,j为第j维个体的数值；α为区间[0,1]内服从正态分布的随机数；(LBj,UBj)表示第j维搜索空间的动态边界，其定义为

LBj=min(Xi,j)

(12)

UBj=max(Xi,j)

(13)

式中：min(Xi,j)、max(Xi,j)分别为第j维个体的最小值和最大值。

当生成的反向解超出(LBj,UBj)边界范围时，使用随机生成的方法进行越界重置，具体描述为

(14)

综合上述，改进的混沌精英黏菌算法(chaotic elite slime mould algorithm, CESMA)可以利用伪代码表述其执行流程，如表1所示。

表1 CESMA算法伪代码Table 1 Pseudo code of CEMSA algorithm

1.3 算法性能测试

为充分验证CESMA算法的有效性和优越性，选取4个基准函数对改进CESMA算法、标准SMA算法、粒子群算法(particle swarm optimization, PSO)[22]、鲸鱼优化算法(whale optimization algorithm, WOA)[8]以及多元宇宙算法(multi-verse optimizer, MVO)[23]进行性能对比。基准测试函数的表达式、维度、取值范围和理论最优值如表2所示。表2中，Sphere(F1)和Rosenbrock(F2)为单峰函数，用于评价算法的收敛速度和优化精度；Griewank(F3)和Rastrigin(F4)为多峰函数，主要用来测试算法是否能够避免局部最优，找到全局最优解；xi为各函数表达式在相应取值范围内第i维度的数值，i∈[1,n]，n为设置的最大维度(即30)。

表2 基准测试函数Table 2 Benchmark functions

在相同实验条件基础上，所有算法参数均与原文献保持一致，种群规模设置为50，最大迭代数为500次，采用MATLAB R2017a编程，计算机操作系统为Windows 10，处理器为Intel i5-10300H CPU @ 2.50 GHz，内存容量为16 GB。为减少随机因素对测试结果的影响，5种算法分别对每个函数独立运行30次，记录求得最优函数值的平均值和标准差，测试结果如表3所示，寻优结果最好的算法已用粗体表示。

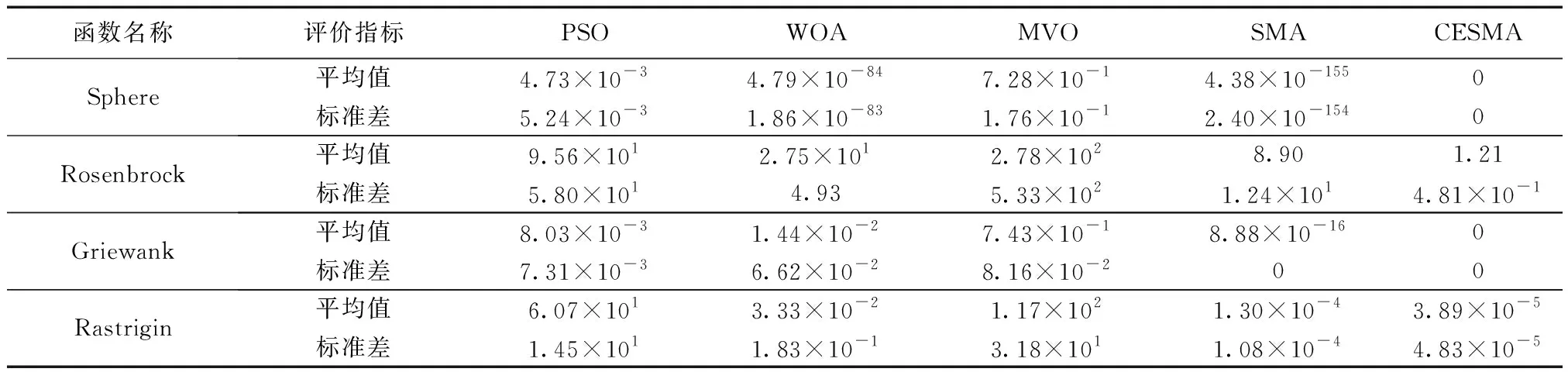
表3 不同算法性能测试对比结果Table 3 Comparison results of the performance of different algorithms

从表3可以看出：在Sphere函数上，CESMA的平均值和标准差均优于标准SMA和其他3种算法；Rosenbrock函数的全局最优值位于一个抛物线型的山谷中，部分智能优化算法很难找到，只有CESMA的结果最近理论最优解；在多峰函数Griewank和Rastrigin上，CESMA的表现依然具有明显优势。5种算法的收敛曲线如图3所示，CESMA比其他4种算法中有着更快的收敛速度和更高的求解精度，进一步证明了改进策略的有效性以及算法的可行性。

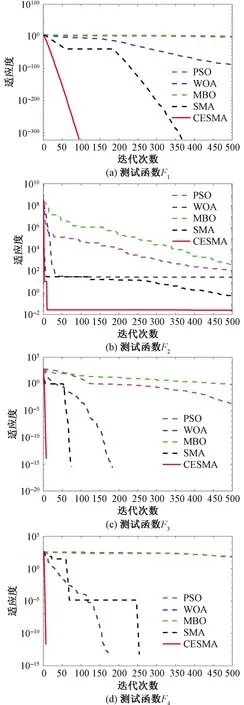
图3 不同算法的收敛曲线Fig.3 Convergence curve of different algorithms

4 基于CESMA的转速控制系统优化

4.1 CESMA-PID控制器设计

传统PID控制器是通过调整系统实际输出值与期望值产生的偏差量实现控制目标[24]，其数学模型为

(15)

式(15)中：u(t)为控制器输出；e(t)为反馈误差；Kp为比例增益系数；Ki为积分时间常数；Kd微分时间常数；不同的Kp、Ki、Kd组合对控制系统的稳定性、响应速度等都有着至关重要的影响，因此如何选择一组最佳的合理控制参数使得系统综合性能达到最优是PID控制的关键。

然而实际工业控制中，传统PID控制器在高度非线性和不确定时参数难以整定，容易导致电机出现转速超调显著、转矩波动明显等问题[25]。根据以上理论分析，BLDCM转速控制系统采用双闭环控制：转速外环采用CESMA动态优化的PID控制器(CESMA-PID)，电流内环采用电流滞环控制器，利用CESMA算法良好的优化搜索能力，能够有效克服传统参数整定方法的缺陷，实现电机平稳运行，如图4所示。

图4 BLDCM转速控制系统结构图Fig.4 Structure diagram of BLDCM speed control system

e(t)=r(t)-y(t)

(16)

式(16)中：r(t)为电动机转速值；y(t)为电机转速反馈值。

根据BLDCM的控制要求，为了获得满意的动态特性本文选用误差绝对值时间积分性能指标作为迭代寻优的适应度函数F主体部分，计算公式为

(17)

式(17)中：ω1、ω2为权重常数，取值范围均在[0,1]；输出u2(t)加入目的是防止控制性能过大。

同时针对超调现象，在性能指标中引入惩罚措施，将超调量作为目标函数中的一项，如式(18)所示：

e(t)<0

(18)

式(18)中：Δe(t)=y(t)-y(t-1)；ω3为权值常数，通常满足ω3>>ω1，故取ω1=0.999，ω2=0.001，ω3=100。

4.2 CESMA-PID控制器实现步骤

采用CESMA算法优化PID控制器参数的具体实现步骤如下。

步骤1 设定种群规模，最大迭代次数，Kp、Ki、Kd的取值范围以及空间维数，利用Tent混沌映射产生初始黏菌个体位置。

步骤2 将当前的黏菌个体位置作为PID参数，根据式(18)计算出个体适应度。

步骤3 更新当前最优个体和及其适应度值。

步骤4 根据式(8)计算W。

步骤5 对于每一个黏菌个体，根据式(6)、式(7)更新参数vb,vc和p，同时根据式(5)更新黏菌个体位置。

步骤6 利用精英反向学习策略产生新的解，更新当前最优个体及适应度值。

步骤7 若算法达到设定的最大迭代次数则输出最优PID控制参数(即黏菌算法的全局最优位置)，否则返回步骤2。

步骤8 算法结束。

初始化种群规模为50，最大迭代次数为100次，空间维度D=3，Kp的取值范围为[0,50]，Ki的取值范围为[0,2]，Kd的取值范围为[0,2]，运行CESMA算法对PID控制器进行优化，得到一组最佳系数为：Kp=35.58，Ki=0.856 7，Kd=0.282 6，同时可以计算出相应适应度函数值为14.454 4，如图5所示。

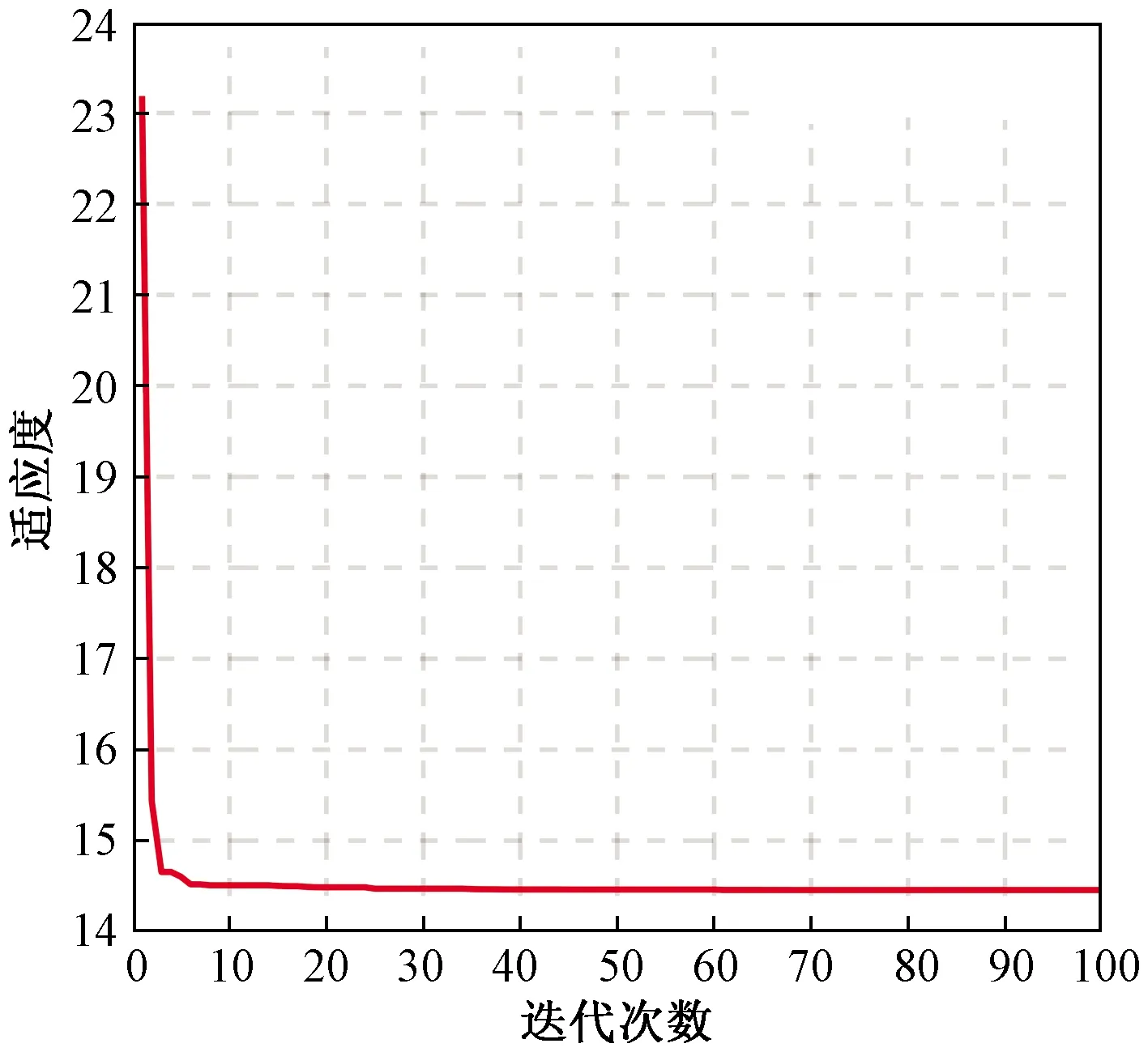
图5 适应度函数曲线Fig.5 Fitness function curve

5 仿真及实验

5.1 仿真分析

在MATLAB R2017a环境中，编写S-Function函数和Simulink模块相结合搭建BLDCM转速控制系统仿真模型进行实验，BLDCM仿真参数如表4所示。为了突出对比效果，仿真转速环分别采用传统PID、模糊PID以及CESMA-PID进行控制，传统PID的初始值根据Ziegler-Nichols法获得分别为：Kp=12.48，Ki=0.657，Kd=0.23；模糊PID采用三角形隶属度函数，由MATLAB的FUZZY工具箱得到模糊规则方阵；CESMA-PID的参数设置同4.2节一致。

表4 BLDCM仿真参数Table 4 BLDCM simulation parameters

首先，系统在变速条件下进行实验，设定空载起动时额定转速n=1 000 r/min，在时间t=0.5 s时，转速下降至n=600 r/min；在t=0.8 s时，加速到n=800 r/min，图6为3种控制器下的转速响应曲线。可以看出：在给定转速设定为n=1 000 r/min时，CESMA-PID可在0.15 s达到稳定状态，传统PID及模糊PID的稳定时间较长均在0.3 s左右；在转速突变为n=600 r/min时，CESMA-PID在0.05 s后重新达到稳态；当给定转速提升为n=800 r/min时，CESMA-PID亦可在0.1 s内达到稳态。由此可见本文提出的CESMA-PID控制器响应速度更快，恢复稳定状态用时最短，控制效果优于其他两种控制方法。

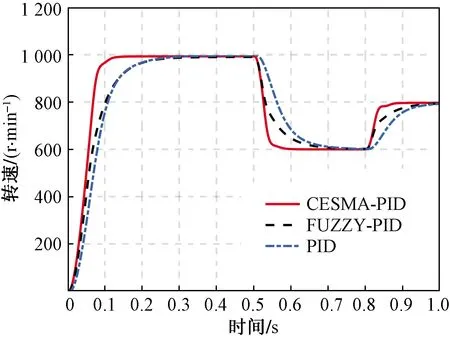
图6 变速条件转速响应曲线Fig.6 Speed response curve with different speed

其次，系统在突加负载条件下运行，设定空载起动时额定转速n=1 000 r/min，在时间t=0.5 s时，加入扰动转矩0.3 N·m，电机转速响应曲线如图7所示。当转矩施加在0.5 s时，传统PID和模糊PID均存在明显扰动，而CESMA-PID的波动最小，恢复稳定状态快，抗干扰能力强。

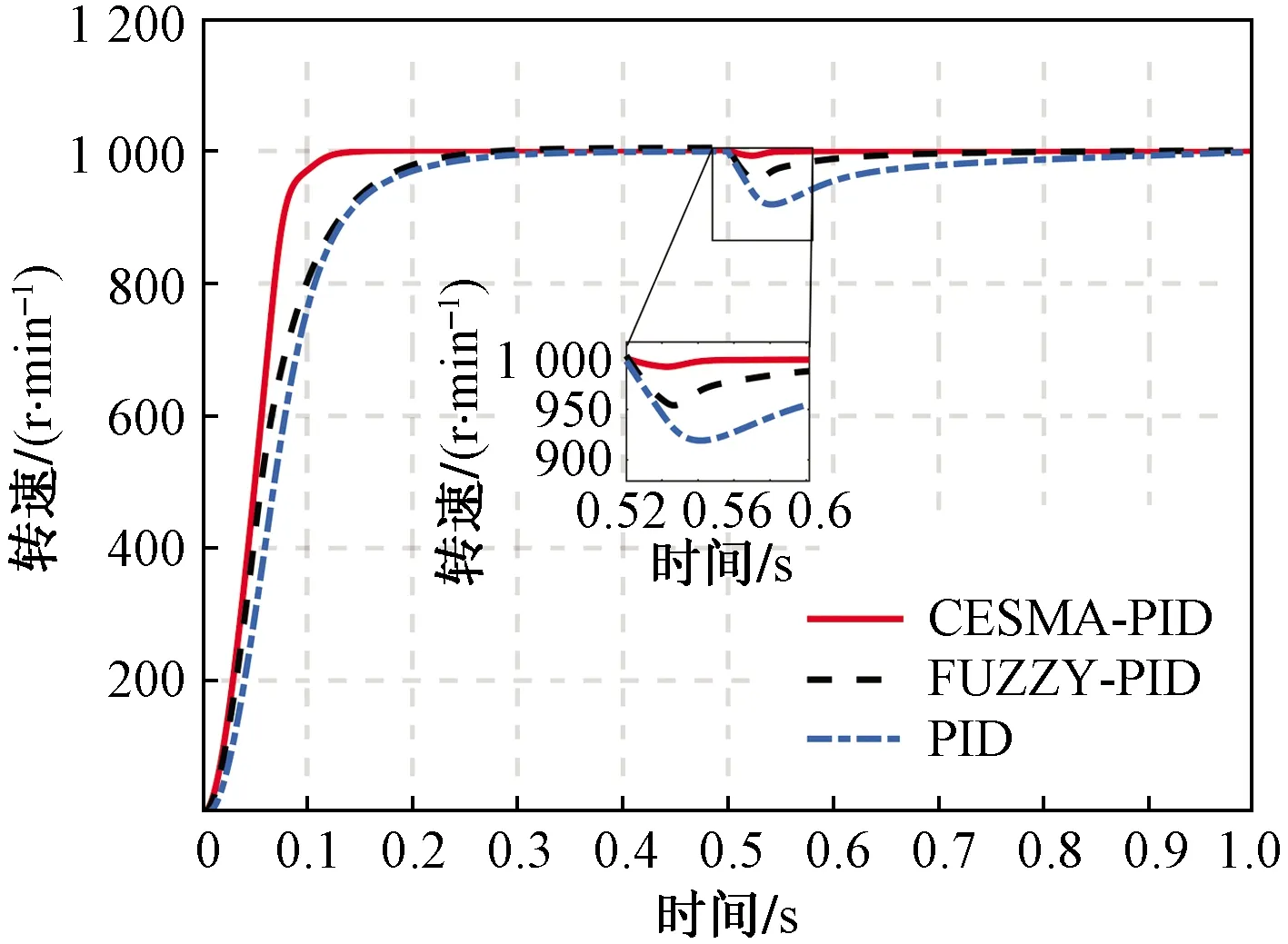
图7 突加负载条件下转速响应曲线Fig.7 Speed response curve under sudden load

最后，对CESMA-PID在转速突变、突加负载条件下的控制性能进行仿真验证，设定空载起动时额定转速n=1 000 r/min，当系统运行到t=0.5 s时，转速下降至n=800 r/min，同时加入0.3 N·m扰动转矩，电机转速响应曲线如图8所示。可以看出，CESMA-PID没有明显超调且响应速度快，可以在0.05 s内达到稳定状态，而传统PID以及模糊PID的稳态时间较长分别为0.68 s和0.70 s。

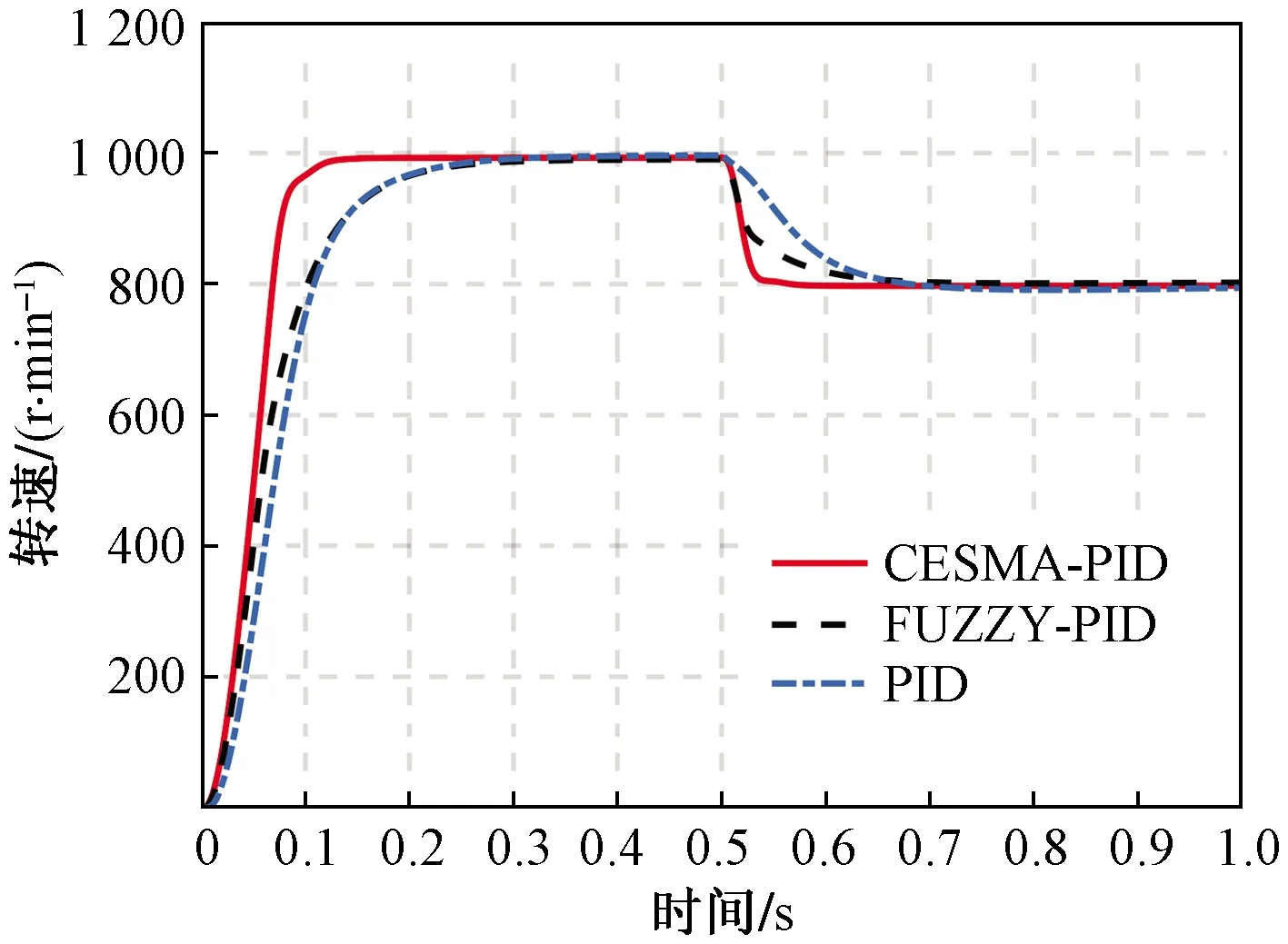
图8 变速、突加负载条件下转速响应曲线Fig.8 Speed response curve under different speed and sudden load

综上仿真结果验证了所提出的CESMA-PID控制器要比传统PID控制器和模糊PID控制器有着更快的响应速度，更高的控制精度和更强的抗干扰能力。

5.2 实验验证

为进一步验证仿真模型的可靠性，搭建了基于意法半导体公司STM32F103ZET6单片机的BLDCM转速控制系统实验平台，系统硬件组成如图9所示。实验所用电机主要规格参数如下：额定电压为24 V、额定功率为100 W、额定转速为3 000 r/min、空载电流为0.8 A、极对数为4。

图9 BLDCM转速控制系统硬件组成Fig.9 Hardware composition of BLDCM speed control system

实验时，令参考给定转速由1 000 r/min下降至600 r/min，经过0.3 s后，再由600 r/min恢复至1 000 r/min，将采集的数据结果以十进制导入MATLAB软件中，3种控制方法对电机的转速控制跟随曲线如图10所示。可以看出，传统PID和模糊PID控制下的电机转速存在超调，稳定时间长，且转速曲线存在一定抖动；而基于本文改进黏菌算法自整定PID控制下的电机转速无超调，转速曲线相对平滑，实验结果再次证明经过CESMA算法优化后的PID控制器动静态性能有着显著提高。

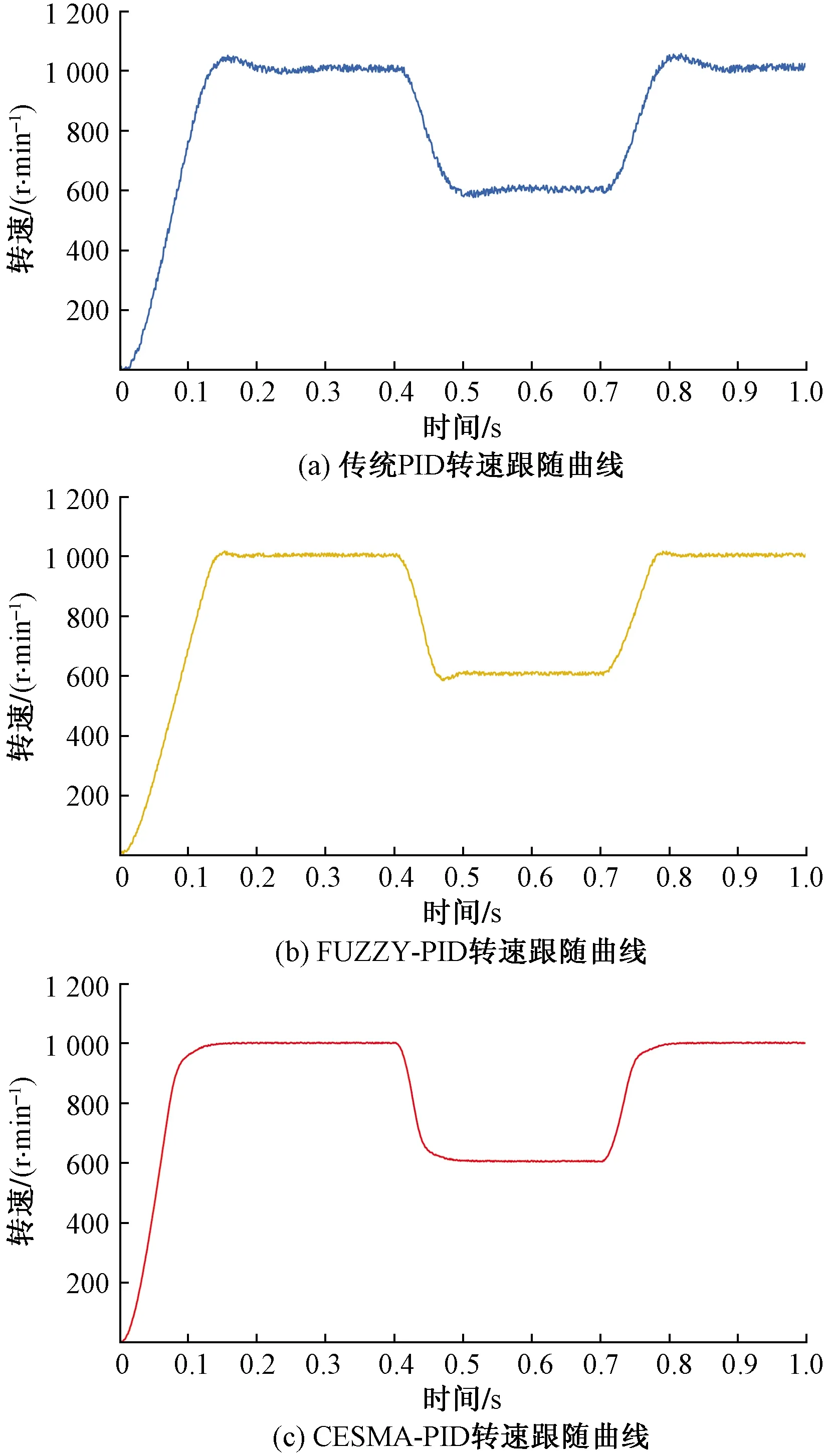
图10 不同控制方法下的转速跟随曲线Fig.10 Speed following curve of different control methods

6 结论

为提高无刷直流电机转速控制性能，提出了一种混沌精英黏菌算法优化的自适应PID控制方法。通过4种典型测试函数验证了改进算法在收敛速度和寻优精度上的优越性，并将其应用于无刷直流电机速度环PID控制器参数自整定。分别在变速、突加负载以及变速与负载共同作用的条件下进行仿真和实验，结果表明本文方法具有响应速度快、超调量小、鲁棒性较强等优势，在其他PID控制的系统中也有着良好的应用前景。