禁飞区影响下的空天飞机可达区域计算方法
2021-10-21章吉力周大鹏杨大鹏刘然刘凯
章吉力,周大鹏,杨大鹏,刘然,刘凯,*
1. 大连理工大学 航空航天学院,大连 116024
2. 航空工业沈阳飞机设计研究所,沈阳 110035
空天飞机是一种能够快速往返于稠密大气层、临近空间和轨道空间的可重复使用飞行器[1-2],既可以像普通飞机一样水平起降,又具备临近空间持续机动飞行能力,具有重要的政治价值、经济价值和军事价值。
可达区域求解[1-2]是对空天飞机的覆盖范围和飞行能力进行评估的重要方法,基于可达区域求解的结果进行任务的继续与中止、目标的决策与切换能够大幅提升飞行器自主性。可达区域的求解方法已受到国内外众多学者的关注。
可达区域的求解方法有很多种,主要有常值倾侧角法[3-4]、剖面平移设计法[5]、优化法[6-14]、剖面参数规划法[15-17]等。由于常值倾侧角法解算出的区域存在一定误差,与实际区域相比偏小,但同时也具有简单易行、稳定性高、解算速度快的特性,因而成为工程中常用的方法。剖面平移设计法首先将再入过程约束转化到H-V剖面,形成再入走廊,之后沿着走廊下边界进行再入剖面规划,形成航程最短的极限剖面,再将该剖面向上平移,形成航程适中的剖面,最后以零倾侧角飞行,形成航程最长的剖面[5],将这一系列剖面的终点连接起来,即得到可达区域。
优化法是现有最为精确的解算方法,但解算速度相对较慢。文献[7-8]基于目标函数变更求解构成可达区域边界的轨迹。优化指标涉及最大纵程、最小纵程,及若干中间量纵程填补边界曲线,最后把这些弹道的落点连起来,即得到可达区域。文献[13]还考虑到优化得到的控制指令的平滑性,认为直接使用伪谱法优化倾侧角和攻角指令得到的剖面可行性差,使用控制变量的二阶导数作为优化变量能够得到更平滑的控制指令。剖面参数规划法介于优化法和剖面平移设计法之间,首先确定一个基准剖面,剖面上有许多待求参数,通过设置与优化法类似的特殊优化指标,来确定这些待求参数,文献[15]采用粒子群优化的方式来求解这些待定参数,文献[16]利用差分进化算法和倾侧角插值求解待定参数,权衡兼顾了可达区域精度和求解效率。
还有学者通过对可达区域特性的分析,以解析和近似的方式来求解可达区域,文献[18]考虑到可达区域同椭圆的近似性,以两个最大横程终点间线段为短轴,以最大纵程终点到短轴距离为半长轴构建半椭圆可达区域。文献[19]通过解析同伦法,在求解4个子优化问题的基础上,通过构造合适的同伦参数延拓出纵向可达区。也有学者将可达区域求解应用于某些特殊场景。文献[20]考虑了在具有路径点约束情况下的可达区域估计方法。文献[21]通过可达区域求解结果指导在轨星座设计方法,构建目标全覆盖的空间战略武器星座。
总的来说,现有的研究中对可达区域的求解方法鲜有考虑禁飞区的影响。主要存在以下难点:一方面,禁飞区与飞行器相对位置的不确定性引发禁飞区对可达区域影响的不确定性,另一方面,禁飞区的引入会对可达区域的形状产生较大不规则改变,难以通过一个统一的方式或算法对影响后的可达区域进行描述。以上难点导致在现有方法中往往从制导层面完成禁飞区规避,在靠近禁飞区时添加额外的规避制导律,这局限了空天飞机的在线自主决策能力。
本文提出一种禁飞区影响下的再入可达区域快速分类与求解方法,直接在评估点基于飞行状态和禁飞区信息求解出禁飞区影响下的可达区域,进而通过射线法判断备选目标点是否位于可达区域以内,对位于可达区域以内的可行目标点,应用分段预测—校正制导方法完成高精度导引。
1 无禁飞区的可达区域求解
1.1 再入动力学模型
空天飞机的再入过程如图1所示,从再入点开始,到能量管理段(Terminal area energy management,TAEM)交接点为止。
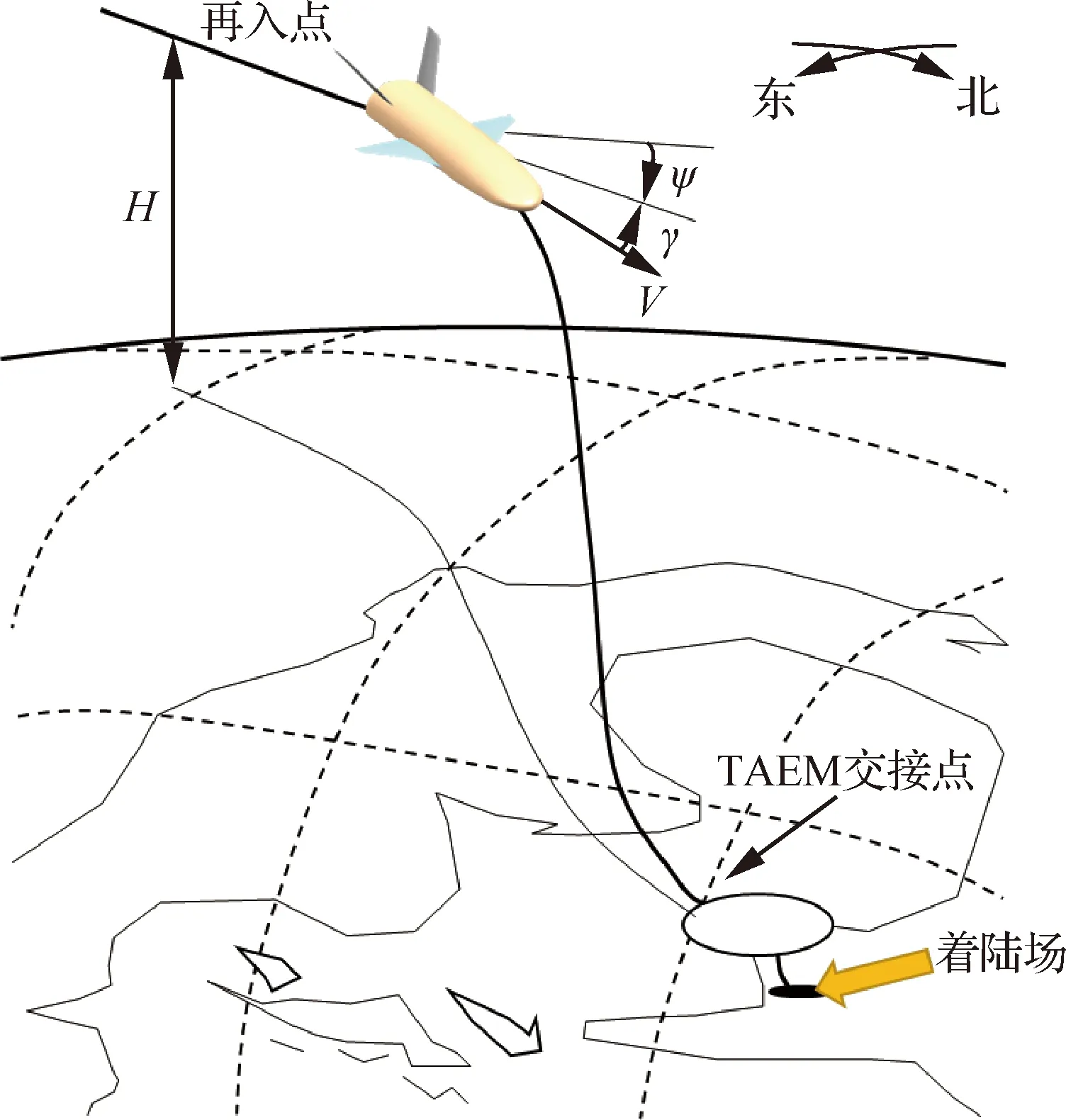
图1 空天飞机再入过程Fig.1 Reentry phase of aerospace plane
空天飞机再入动力学模型在弹道坐标系中建立,采用倾斜转弯模式(Bank To Turn, BTT),整个再入过程均为无动力状态,在考虑球形大地和地球自转的基础上,三维质点动力学模型为
(1)
式中:V为速度;γ为弹道倾角;ψ为弹道偏角;r为地心距,表示飞行器到地心的距离;λ为飞行器在地表投影点的经度;φ为飞行器在地表投影点的纬度;g为重力加速度,其中g0=9.806 7 m/s2;m为飞行器的质量;ωe为地球自转的角速度;σ为倾侧角;D为阻力;L为升力,具体计算方式为
(2)
式中:ρ为大气密度,可以视为高度的函数;A为参考面积;CL为升力系数;CD为阻力系数。再入过程的控制变量一般只有迎角α和倾侧角σ,在设计再入弹道的过程中,迎角α的值由事先设定好的α-V剖面给出:
(3)
典型的再入过程约束由式(4)~式(6)给出:
(4)
(5)
(6)

再入终端满足地心矩(高度)、速度约束:
(7)
高度和速度又可以用近似能量的方式来进行统一表征:
(8)
所以式(7)表示的终端状态约束还可以采用能量形式表达为
ef=eTAEM
(9)
式中:ef为终端能量;eTAEM为相应的能量约束。


图2 约束转化得到的倾侧角幅值边界Fig.2 Boundary of bank angle translated from constraints
倾侧角幅值满足约束:
|σ|≤|σ|max
(10)
基于对再入过程的约束与定义,本文后续的可达区域计算的终点为TAEM交接点而非降落点。
1.2 不考虑禁飞区的可达区域求解
常用的可达区域求解方法主要包括常值倾侧角法和优化法。由于可达区域求解本质是基于某个特定状态点对飞行器的飞行能力进行评估,因此,后续称该初始状态点为评估点。
当不考虑禁飞区约束时,常值倾侧角法是求解可达区域最简单、快速、有效的方法。常值倾侧角法以任一评估点出发,采用恒定的倾侧角值作为指导指令,积分生成轨迹直至满足终端约束。通过在[-|σmax|,|σmax|]之间以适当的间隔选取一系列指令值,可以对应生成一系列轨迹,在经度—纬度剖面内将这一系列轨迹的终点连接起来,即构成飞行器在当前初始状态下的可达区域。利用常值倾侧角法求解可达区域的示意图如图3所示。

图3 常值倾侧角法求解可达区域Fig.3 Reachable domain obtained by constant bank angle method
常值倾侧角法的算法本质只有积分过程,因而算法稳定性好,计算速度较快,但受限于制导指令的单一性,求解出的可达区域并不完全精确,与实际可达区域相比偏小。
优化法通过多次更改目标函数生成特定轨迹来求解可达区域。首先,以任一评估点为优化的状态初值,设置目标函数为航程最大和航程最小,求解出对应的轨迹并记录最大、最小航程的值Lmax和Lmin;之后,设置优化指标为横向航程最大,并将航程固定为Lmax和Lmin的中间量:Li=Lmin+wi(Lmax-Lmin),对wi在[0,1]之间进行一系列的取值,得到对应的一系列优化轨迹。即求解系列优化问题:
(11)

图4 优化方法求解可达区域Fig.4 Reachable domain obtained by optimization method
优化方法得到的边界虽然相对更加准确,但由于其底层依赖于复杂的非线性规划求解器,实际应用中,一旦引入禁飞区约束,难以保证算法在求解各条轨迹时均能够快速收敛;同时,运算时间长是一般优化算法的通病,这也束缚了它的在线应用前景。综上所述,对于禁飞区影响下的在线可达区域求解,单纯地使用上述2种方法均很难达到目的。
2 禁飞区影响下的可达区域求解
2.1 禁飞区对可达区域的影响特性分析
对于空天飞机这类具有较明显升力面结构的飞行器,其再入的可达区域是一个缺角的近似椭圆,形状如图5所示。而禁飞区(图中阴影部分N处)的引入,实质上是在原有的可达区域中引入了一片不可达区域,但这片不可达区域的形状是不确定的。


图5 禁飞区对可达区域的影响Fig.5 Influence of no-fly zone on reachable domain
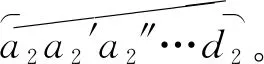
由此,Rd1 d2f在禁飞区的影响下,初始可达区域Rabc中有两片区域变得不可达,分别是子区域右侧的RcQ1c1eQ2c2c和子区域左侧的Rd1 d2f。
针对图5中的诸元,存在一些关系需要补充说明。因此作出如下假设:
假设1示意图中的可达区域是“充分必要”的,它能完整地反映飞行器飞行能力,也即:任何区域内的点均是可达的,任何区域外的点均是不可达的。区域内的所有点(λt,φt)满足式(12):
∀ (λt,φt)∈Rabc
∃σ(t)
(12)
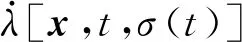

基于以上两点假设,图5中的诸元满足推论1和推论2。
推论1Ra1b1c1⊆Rabc,Ra2b2c2⊆Rabc
由禁飞区带来的影响,只会导致原先可到达的区域,现在不可到达了,而不会使得原先不可到达的区域变得可到达。因此,从T1和T22个子评估点出发得到的子区域Ra1b1c1和Ra2b2c2均应位于原可达区域abc以内。
推论2Ra1b1c1和Ra2b2c2同Rabc相切,切点是Q1和Q2

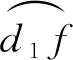


图6 简化的“充分”可达区域Fig.6 Simplified "sufficient" reachable domain
1) 轨迹从禁飞区下(上)侧经过,与禁飞区相切。
2) 轨迹终点是该侧子区域的上(下)边界点。
称这样的轨迹为极限绕飞轨迹。极限绕飞轨迹在切点前的部分与相切轨迹重合,在切合点后的部分是以最大倾侧角幅值飞行产生的轨迹。
由极限绕飞轨迹与该侧的相切子区域围成的可达区域在图中用色块标记。由于极限绕飞轨迹实际并未达到飞行器的飞行能力极限,同时该轨迹下侧的区域均在飞行能力覆盖范围内,因此得到的可达区域是“充分”的,即可达区域以内的点均是可以到达的。
对于子区域数量可能随着禁飞区位置的变化发生改变的问题,在求解子区域之前,引入禁飞区分类策略,针对存在0个、1个、2个子区域的情况,实施分类求解。
禁飞区影响下的可达区域求解算法流程如图7所示。
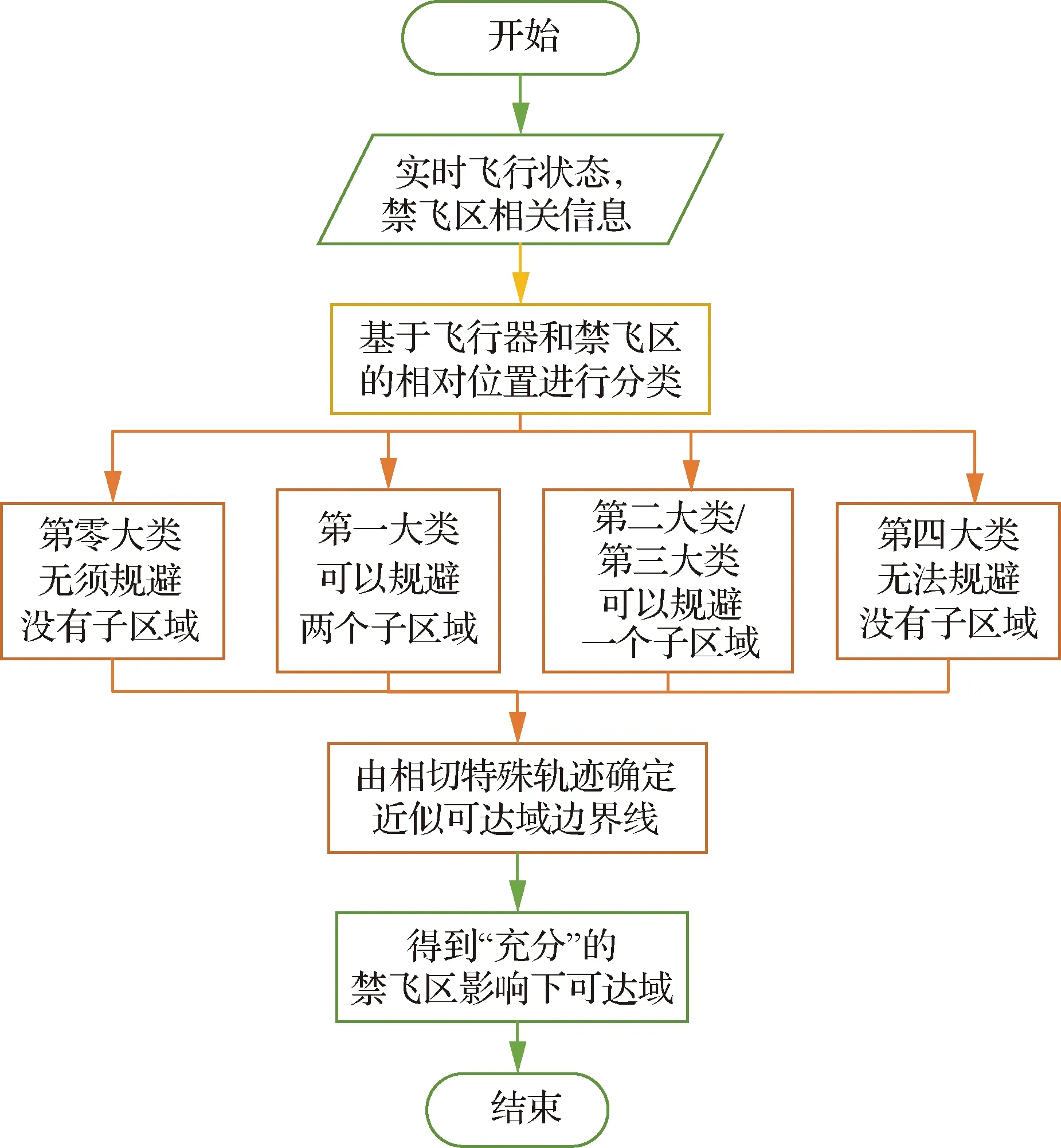
图7 禁飞区影响下的可达区域求解算法流程Fig.7 Flow chart of algorithm for obtaining the influenced reachable domain
2.2 禁飞区对可达区域的影响特性分类
在2.1节中,给出了一般情形下禁飞区对可达区域的影响特性,在实际情况中,受禁飞区与飞行轨迹相对位置的影响,对于2.1节图5给出的诸元,可能并不总是全部存在,比如有时飞行器可能只能从禁飞区的某一侧通过,则对应的子区域也只有一个。为此,需要对这些情况进行分类讨论。图8给出了不同类的禁飞区位置示意图。

图8 不同类的禁飞区位置示意图Fig.8 Diagram of different classes of no-fly zones
需要指出,本节和后续2.3节实现的是实际可能面对的多种复杂情形下图5中子区域Ra1b1c1和Ra2b2c2的求解。
对禁飞区进行分类的标准遵循禁飞区与3条特殊轨迹的相对位置。Lmax为最大航程轨迹,+Lmin和-Lmin分别为下侧和上侧的最小航程轨迹。
对于经度—纬度剖面内的任一条轨迹,可用矩阵[λi,φi]表示:
(13)
定义轨迹距离S为轨迹到禁飞区圆心的最短距离,由式(14)给出:
(14)
式中:λn为禁飞区圆心的经度;φn为禁飞区圆心的纬度。轨迹同禁飞区的关系标识由式(15)给出:
(15)
式中:1为相交;0为相离;Rn为禁飞区的半径。由位置关系(相交或相离) 可将禁飞区分为4个大类,8个小类。如表1所示。

表1 基于同Lmax,+Lmin&-Lmin相对位置关系的禁飞区分类
对于禁飞区同3条特殊轨迹均相离的情况,仍然存在第0类,1-B类和1-C类3种情形,可以按照式(16)原则进一步划分:
(16)
式中:N表示禁飞区;[λmax,φmax]为Lmax对应的轨迹点经纬度;φmax([λmax,φmax]|λn)为Lmax在λ=λn处的插值纬度。
对第一大类,禁飞区影响下的可达区域存在2个子区域,即对应2.1节图5中的Ra1b1c1和Ra2b2c2;第二大类和第三大类,禁飞区影响下的可达区域仅存在一个子区域,对于第零大类和第四大类,禁飞区影响下的可达区域不存在子区域。更多细节在表2中展示。

表2 不同分类的禁飞区规避策略
2.3 相切轨迹搜索与子区域生成
综合考量效率和稳定性,本节基于常值倾侧角对应的一系列轨迹,采用二分法搜索相切轨迹,再从相切点(子评估点)T1,T2出发计算子区域。
由常值倾侧角法计算轨迹落点的方法如式(17)所示:
(17)
式中:σc的取值为
(18)
依据待搜索轨迹所在的大致区域,算法由两对共4个二分法搜索环节构成,4个环节分别称Up1,Up2,Down1和Down2。以0°倾侧角对应轨迹Lmax为边界,Up区为上半区,Down区为下半区;1代表禁飞区左侧,2代表禁飞区右侧。图9给出了搜索区域以及搜索的目标轨迹。

图9 搜索区域示意图Fig.9 Diagram of search area
(19)
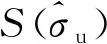
(20)
相切轨迹求解流程见①~③
① 在单个搜索区内找到一条与禁飞区相交的轨迹[λstart,φstart],轨迹对应的倾侧角值为σstart,作为初始搜索区间的边界。其中,Up1和Down1初始搜索区间在[λstart,φstart]左侧,Up2和Down2初始搜索区间在[λstart,φstart]右侧。
② 定义轨迹距离S为目标函数,对任意的倾侧角值σu,有其对应轨迹[λu,φu]及最短距离值S(σu)
(21)
(22)
4个环节的主要差异在初始搜索区间,如表3所示。

表3 不同环节搜索区域和初始区间
依据分类结果,需要分别采用不同的环节,在不同区间搜索相切轨迹,具体如表4所示。

表4 各分类应用环节
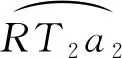
需要指出的是,对于部分升阻比偏高的飞行器,其地面轨迹在末段可能出现绕回现象,即在低速、大倾侧时,弹道偏角在短时间内就会发生较大改变。本文给出的方法适用于不发生绕回现象的情况。
3 可达性判定与制导
3.1 可达性判定方法
在求解得到可达区域以后,若想要辨明某个目标点是否位于可达区域内,还需要设计在线判定算法。
对于不考虑禁飞区的情形,可达区域的边界相对简单,即第2章中所述区域Rabc。在仿真与实际应用中,根据2.3节提到的可达区域求解方法,Rabc并非是由解析方程确定的椭圆,而是通过若干个边界点的连接来确定的凹多边形。对于平面内任意多边形区域,均可以采用射线法判断来点是否位于区域内,如图10所示。

图10 射线法示意图Fig.10 Diagram of ray method
所谓射线法,是从被测点向任意方向作一条射线,判断射线与多边形边界的交点数量。如果交点的数量为奇数,则被测点在多边形内;如果交点的数量为偶数,则被测点在多边形以外。应用该方法即可判定是否有目标点位于可达区域内。
3.2 考虑禁飞区规避的分段制导方法
预测校正方法是近年来热门的在线再入制导方法,许多学者进行了相关研究[24-25]。本文采用一种分段预测—校正制导方法,具体逻辑详见文献[26]。
该方法与传统预测—校正制导的主要区别有两点:一是在纵向制导环引入分段目标函数,如下所示:
(23)
式中:Sp为当前点到预测落点的距离;S0为当前点到目标点的距离;Sfp为目标点到预测落点的距离。各项参数的具体计算方法也可参见文献[26]。
二是引入了禁飞区规避逻辑,当飞行器抵近禁飞区时,采取倾侧角反转或增大倾侧角幅值的策略来完成规避。
4 仿真校验
4.1 禁飞区影响下的可达区域分类仿真
综合考量效率和稳定性,本文采用常值倾侧角法在评估点R和子评估点T1,T2计算可达区域和子区域,需要注意,由于常值倾侧角法求解可达区域与实际的可达区域相比相对偏小,仿真中实际计算得到的区域无法严格满足推论1和推论2,最终所得影响下可达区域与实际影响下可达区域相比也相对偏小,即得到禁飞区影响下的可达区域是“充分”的结果。
以空天飞机的再入阶段为例进行仿真分析,仿真对象为某具有升力结构的空天飞机,再入点的初始状态由表5给出。

表5 纵向初始条件
首先,沿最大航程轨迹Lmax布置大量禁飞区,禁飞区的半径均为200 km。布置结果如图11所示,图中,实线边界为不考虑禁飞区的情形下得到的初始可达区域(即Rabc),虚线为最大航程轨迹Lmax,即0°倾侧角对应轨迹。
采用本文所述算法对图11所有禁飞区进行分类,分类结果如图12所示。

图11 禁飞区分布示意图Fig.11 Distribution diagram of no-fly zones

图12 禁飞区分类结果Fig.12 Classification results of no-fly zones
仿真结果表明,算法能够稳定高效地完成对经度/纬度剖面内的禁飞区的分类,用以支撑后续可达区域求解过程。
4.2 禁飞区影响下的可达区域求解仿真
对于不同分类的禁飞区,需要采用不同的搜索环节搜索相切轨迹和进行子区域求解。在图12中任意选择每一类的禁飞区进行可达区域求解,选取的禁飞区圆心位置在表6中给出。最终得到禁飞区影响下的可达区域如图13~图15所示。
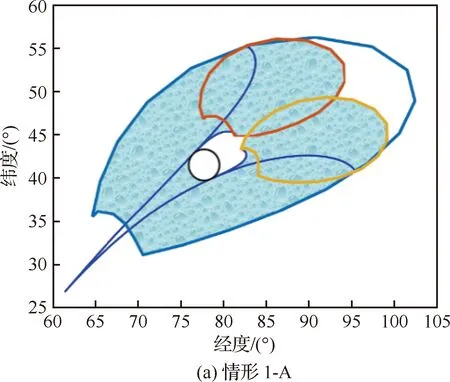
图13 情形1-A,1-B,1-C仿真实例Fig.13 Cases 1-A,1-B and 1-C simulation example
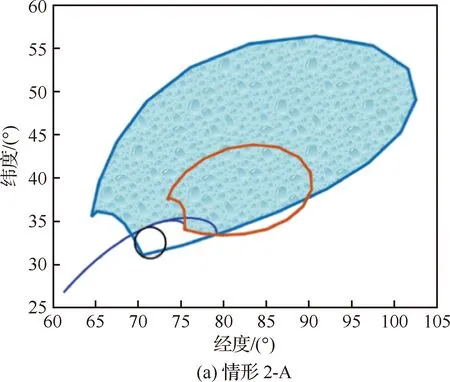
图14 情形2-A,2-B仿真实例Fig.14 Cases 2-A and 2-B simulation example

图15 情形3-A,3-B仿真实例Fig.15 Cases 3-A and 3-B simulation example

表6 各类禁飞区圆心位置
图中,大椭圆边界为初始可达区域(即图5中的Rabc),小椭圆边界为子区域(即图5中的Ra1b1c1和Ra2b2c2),圆形为禁飞区,禁飞区影响下的可达区域在图中用色块填充。
仿真结果表明,算法对不同位置的禁飞区实现了有效分类,并基于分类结果求解得到了相切轨迹、极限绕飞轨迹和子区域,最终获得禁飞区影响下的可达区域,对于经度—纬度剖面内任意位置、任意分类的圆形禁飞区,在不超过飞行器物理能力的前提下,算法均能够稳定地实现可达区域求解。
结合本文仿真对象实际情况,可以给出本文所述方法的一个初步适用范围,对升阻比在2以下的飞行器,取末端能量条件HTAEM=21.9 km,VTAEM=764 m/s时,能够应用上述方法实现飞行能力评估。
5.3 面向可达区域内目标点的规避制导仿真
以图13(a)情形1-A的禁飞区为基础进行本节仿真,初始条件与表5中完全一致。在图13(a)所示的区域中选择了两个位于可达区域内的目标点:
(λf1,φf1)=(90°,45°)
(λf2,φf2)=(80°,35°)
仿真结果如图16和图17所示。从图中可以发现,对于选取的2个目标点,算法可以有效实现将飞行器向目标点导引,并且飞行轨迹不经过禁飞区。

图16 面向目标点1导引的飞行轨迹Fig.16 Trajectory of guidance to Target 1

图17 面向目标点2导引的飞行轨迹Fig.17 Trajectory of guidance to Target 2
表7数据显示,相比于单段目标函数预测—校正制导方法[23],引入分段目标函数后的制导精度有较明显提升。

表7 落点误差对比
5 结 论
1) 分析了一般情形下禁飞区对可达区域的影响特性;结合实际飞行中可能存在的禁飞区与飞行器的相对位置情况,提出借助最大航程轨迹Lmax、上侧最小航程轨迹-Lmin和下侧最小航程轨迹+Lmin,对经度/纬度剖面内禁飞区存在位置展开分类。
2) 依据分类结果,分别求解相切轨迹、极限绕飞轨迹和子区域;通过子区域和极限绕飞轨迹确定可达区域与不可达区域的边界线,得到禁飞区影响下的可达区域。
3) 介绍了判定目标点是否位于可达区域以内的射线法和可以应用于可达区域以内目标点的分段预测校正制导方法。
4) 通过数值仿真验证了提出算法的有效性和稳定性。对于经度/纬度剖面内散布的禁飞区,算法均能实现可达区域的求解。对确定位于可达区域以内的目标点,通过应用分段预测校正方法,能够实现导引并满足终端精度要求。
