基于学生概括理解能力的数学概念教学

韩晓晓

摘要：概括是学生学习数学知识、概念及数学思想方法的重要思维形式，是学生理解数学本质的基本活动。本文以初中数学《变量与函数》的教学为例，引导学生从实际情境中抽象出函数模型，并归纳概括出函数概念，通过具体行为表征实现对函数概念的理解与应用。课堂的教学设计从以下五个方面展开：创设有效情境、问题驱动、抽取筛选、属性归类、明确常量和变量;引导学生关注“变化过程中数量的变化”，探究两个变量之间的对应关系，让学生主动形成、自主概括归纳概念的本质，指导学生从解析式、表格、图象、初步映射等多样形式全方位理解，体会知识承载的数学思想，进而核心素养。

关键词：数学概括理解能力 函数的概念 建构学习 有意义学习

数学概括理解能力[1]是体现学科核心素养的重要指标。概括理解是学生学习数学知识、概念及数学思想方法的重要思维形式，行为表现特征有自主性、渐进性、外显性、互动性和严谨性。概念的教学涉及“概念的名称、定义、相关和无关特征、正例和反例”四方面，教学过程中，注重学生的思维过程，学生自主逐步形成函数的概念，有针对性的选择例题和练习题，有助于推动学生再去概括和辨别，实现学生对概念学习记忆、理解、运用的结果，达到理解的六侧面-能解释，能阐明，能应用，能洞察，能深入，能自知。

数学课堂的灵魂是什么？是思想，也就是数学教学过程应该是传授思想的过程.思想是通过什么来展现的？是问题[2]，换句话说，数学课堂应该是围绕问题展开，将驱动教学的问题通过适当的情景展示出来，形成问题情境。本节课情境有：

（1）汽车以60km/h的速度匀速行驶，时间为t h，路程为s km。

（2）电影票价40元/张.设某场电影售出的票数是x张，票房收入为y元。

（3）实物演示弹簧秤，测得弹簧的长度y（cm）与所挂物体的质量x（kg）之间有下列关系：

驱动问题：①每个变化过程中有几个量，是否需要分类？有几个变量？②在变化过程中，两个变量之间有什么关系？ ③聚焦到对应关系，是怎么对应的呢？

问题的设置意在引导学生从具体事物中区分出个别的非本质的属性特征和共同的本质的属性特征，并舍弃个别的非本质的属性特征而抽取出共同的本质属性.数学的抽象完全舍弃了事物的质的内容，而仅仅保留了它们的量的属性[3].两个变量之间的关系有很多，学生容易答出一个量随着另一个量的变化而变化这种联动关系，可以稍微引导这个变化中有没有规律性的变化，即函数的性质。但本节课先聚焦到“函数的本质是两个变量和两个变量之间的对应关系”。从解析式[4]、表格、初步映射和函数示意图等多个角度分析对应关系，会让学生渐进性形成函数概念，突出重点突破难点，而后紧跟练习，如下：

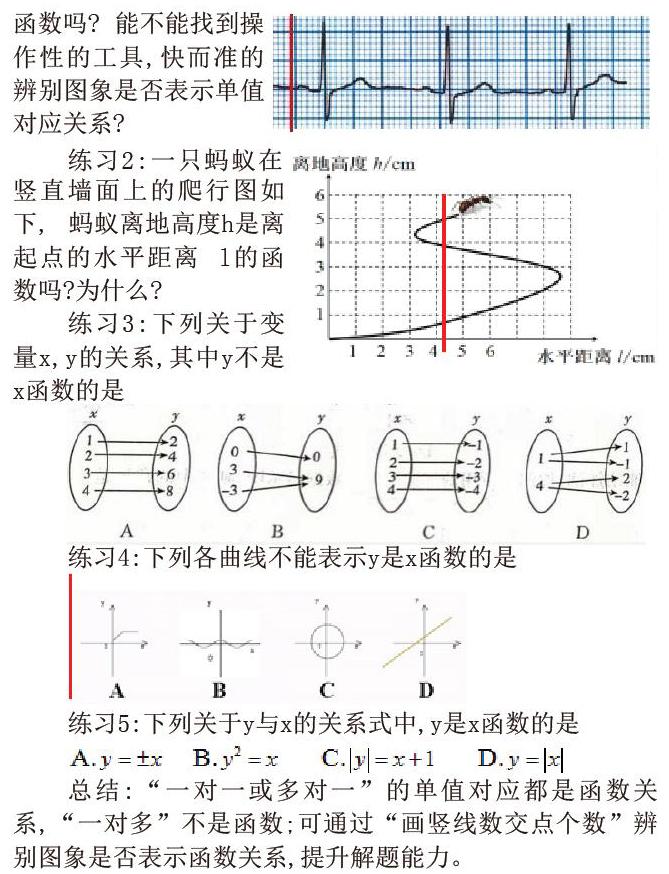
练习1：体检时的心电图，图上点的横坐标x表示时间，纵坐标y表示心脏部位的生物电流， x，y是两个变量， y是x的函数吗？ 能不能找到操作性的工具，快而准的辨别图象是否表示单值对应关系？

练习2：一只蚂蚁在竖直墙面上的爬行图如下， 蚂蚁离地高度h是离起点的水平距离 l的函数吗？为什么？

练习3：下列关于变量x，y的关系，其中y不是x函数的是

总结：“一对一或多对一”的单值对应都是函数关系，“一对多”不是函数;可通过“画豎线数交点个数”辨别图象是否表示函数关系，提升解题能力。

课堂教学中注重学生的思维过程，遵循以结果为导向，以学生的理解到位为主，明确学生通过设计的内容，会获得怎样的理解和应用能力？用怎样的学习支架能引导学生理解重要观点？希望学生如何应用这些观点明确实施的意义？

建构主义和有意义学习理论。学生对现实原型进行数学弱抽象，如案例中最初的3个情境以及心电图、温度变化、映射、关系式等若干不同例子，引导学生进行反复感知、分析、比较、抽象，聚焦研究两个变量之间的依赖关系，加以归纳概括，得出本质属性，从而形成函数概念，是有意义的构造性活动实践，是借助归纳概括进行的逻辑建构。本节课“函数”这个具体概念的学习适合采用概念形成方式，是上位学习，教学时注重组织学生进行以科学探究为主的一系列师生互动活动，进而应用认知发展教学方式使学生认知系统完成建构.而本章后续“正比例函数、一次函数”等定义性概念的学习方式更适合采用概念同化的方式，是从上位到下位的学习，教学时注重讲授法的运用。

多元课堂互动。本节课尊重学生的差异性，采取了多元的课堂互动。互动活动多样化，能充分调动学生课堂参与度.如站起来回答问题，让学生上讲台讲述观点.尤其是本节课选择题通过亮手指表达观点，亮手指反馈适合选择题和部分填空题，选择题的ABCD选项对应手指1234，一是提供时间和空间让学生独立思考，肯定做得快的同学，又让答对的薄弱生站起来表达，增强数学学习自信心;二是课堂针对性辅导，抓住契机转变错误观念，解释并及时学生的错误观念、创设认知冲突、构建新观念，让整个课堂有效和高效，使学生的思维有深度。