基于深度强化学习的旋转机械故障诊断策略
2021-10-20龙舰涵
龙舰涵
(泸州职业技术学院电子工程学院,四川 泸州646000)
1 引言
旋转机械目前被广泛用于包括石油、能源和化学工业在内的各种工业应用领域,机械故障可能会造成巨大经济损失甚至灾难性事故[1]。随着可靠性相关理论的发展,旨在监测、评估、诊断和预测机械健康状态的研究引起了学者们的广泛关注[2,3]。
深度学习作为一种机器学习算法,可以通过多个非线性变换和近似复非线性函数,从原始数据中自适应地学习层次表示,实现故障诊断[4]。文献[5]提出了一种智能诊断方法,它可以自动地从旋转机械的频谱中挖掘出故障特征,并对其健康状况进行分类。文献[6]使用了卷积神经网络,可以用于诊断滚动轴承的故障,学习滚动轴承的层次特征表示。文献[7]利用基于递归神经网络的自动编码器来处理从旋转机器收集的多个时间序列数据。但是,上述方法仍然存在两个主要缺陷:(1)无法在原始数据和相应的故障模式之间建立直接的线性或非线性映射,且这些故障诊断方法的性能取决于构建和训练深度模型的质量[8]。(2)这种方法的训练机制主要基于监督学习或半监督学习,这意味着诊断算法需要专家系统以便专门学习不同的故障模式[9]。
深度强化学习(deep reinforcement,learning,DRL)涉及强化学习和深度学习的结合,这种结合使人工代理可以直接从原始数据中学习其知识和经验。深度学习能使代理感知环境,而强化学习能使代理学习应对现实问题的最佳策略[10]。考虑到上述问题,提出了一种基于堆叠式自动编码器(stackable automatic encoder,SAE)与深度Q网络(deep Q network,DQN)的深度强化学习机械故障诊断方法。
2 深度Q网络
2.1 Q学习
作为一种无模型的强化学习算法,Q学习也可以被视为一种异步动态编程方法[11]。Q学习算法创建一个表,它可以计算每种状态和动作的最大预期未来奖励。具体来说,列是动作,行是状态。每个单元格的值是给定状态和动作的最大预期未来回报。该表称为Q表,其中“Q”代表操作质量。每个Q表得分是只要代理在相应状态下采取行动,代理就会获得的最大预期未来回报。换句话说,通过搜索与状态相对应的行中的最高Q值,代理始终知道针对每个状态采取的最佳行动。Q学习代理的学习过程可以概括为三个步骤:(1)代理基于对当前状态的观察尝试行动;(2)环境会立即回馈有关行动的反馈,包括奖励或罚金;(3)算法使用Bellman方程基于奖励、行动和状态来更新Q表。
Q学习算法可用于通过Q函数学习Q表的每个值。Q函数定义为:

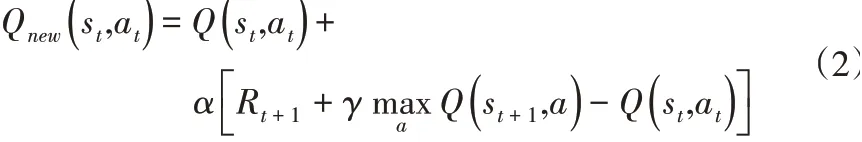
Q学习算法的核心训练过程可以总结如下。
第一步:初始化Q表。
第二步:基于Q表在当前状态st中,选择一个动作来开始学习过程。
第三步:执行动作at,并且观察下一状态st+1和奖励Rt+1。
第四步:通过上面介绍的Bellman方程更新Q表。重复上述步骤,直到训练过程达到预定义的终端条件。
2.2 深度Q网络
DQN可以是新开发的端到端的强化学习代理,它利用DNN来映射动作和状态之间的关系,类似于Q学习中的Q表,诸如CNN、堆叠式稀疏自动编码器和RNN之类的DNN能够直接从原始数据中学习抽象表达[13]。DQN代理必须通过一系列观察、动作、奖励与环境进行交互,这类似于Q学习代理所面临的任务。与DQN代理相比,传统Q学习代理的最严重缺陷在于处理包含大量状态与动作的问题时,使用Q表来映射动作和状态之间的关系可能会导致维数灾。因此,这里使用一个深层的CNN来逼近最佳Q函数,而不是使用Q表。
另外,当Q函数通过非线性函数逼近器表示时,增强学习会变得不稳定或发散。不稳定的原因有两点,一是观察序列中存在的相关性,二是对Q值的小幅度更新可能会导致代理策略以及Q值与目标值之间的相关性发生重大变化。因此,引入了两种称为记忆重放和迭代更新的策略来克服此类缺陷。
记忆重放通过消除观察序列中的相关性,并通过随机化数据来平滑数据分布的变化来解决该问题。迭代更新通过定步长逼近目标值更新Q值从而减少Q值和目标值之间的相关性。首先,记忆重放在每个时间步骤存储代理的经验,以便形成一个包含一定数量经验的名为记忆的集合。在时间步骤t的单次经验et定义为et=(st,at,rt,st+1)在时间步骤t处的记忆定义为Dt,其中然后,在更新DQN代理时,经验重放会从记忆中随机抽取经验,从而达到平滑数据分布的目的。
通常,强化学习算法使用Bellman方程作为迭代更新来估计动作-值函数。但是此方法在实践中不切实际,因此,人们通常使用函数逼近器估算动作-值函数。DQN使用CNN作为函数逼近器,权重作为Q网络。因此,可以通过减少Bellman方程中的均方误差,然后再通过在迭代处更新参数来训练Q网络。因此,在每次迭代改变的损失函数定义为:

区分与权重有关的损失函数的结果为以下形式:
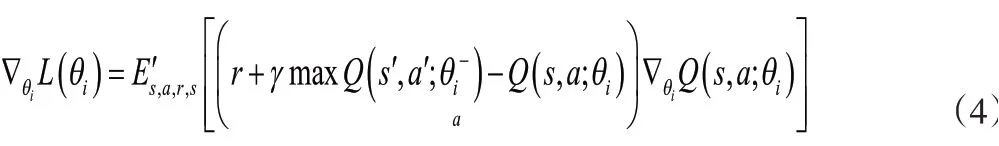
通过Q函数的定义和微分形式,可以进行目标优化。此外,通过在每个时间步骤后更新权重,使用单个样本替换期望值并设置θi-=θi-1,可以在上述框架中恢复Q学习算法。
在DQN的训练过程中,对Q学习进行了两次修改,以确保DNN的训练过程不会发散。第一次是经验重放,其中,通过将当前时间步骤的状态、动作和奖励以及后续时间步骤的状态进行堆叠,将代理的体验存储到重放内存中。经验重放是一种有效的技术,它可以避免参数的波动或分散,通过使代理能够考虑其在学习过程中的经验来平滑学习。Q学习的第二次修改是使用单独的网络在Q学习更新过程中生成目标,并且这种修改可以显着提高DQN的稳定性。此类的方法可以在更新Q值的时刻与更新可能引起的相应影响之间增加延迟,从而减少DNN参数中存在的发散或振荡的可能性。
3 基于DQN的端到端故障诊断方法
通常在诸如博弈论、控制论、运筹学和多智能体系统等领域研究强化学习。故障诊断通常被认为是通过监督学习解决的分类问题[14]。基于监督学习的故障诊断方法需要同时获取故障数据和相应的标签作为区分故障模式的输入。对于基于强化学习的方法,故障诊断代理的学习性能是通过整体奖励来评估的,这与代理在监督学习方法中使用的反馈相比,对于代理调整其性能的反馈要弱得多。换句话说,在学习过程中,代理无法从输入信号中分辨出哪些样本没有被很好地学习。这种机制迫使代理发现故障模式之间的内在差异,从而使代理更加有力。
为了实现基于DRL的故障诊断方法,设计了一个故障诊断仿真模型,通过该模型可以将监督学习问题转换为强化学习问题。这种环境可被视为“故障诊断博弈”模型。每个博弈模型都包含一定数量的故障诊断问题,并且每个问题都包含故障样本和相应的故障标签。当代理正在进行博弈时,博弈将有一个问题供代理诊断。然后,博弈将检查代理的答案是否正确。博弈的奖励机制是答对得一分,答错减一分。博弈结束后,代理将获得总的博弈得分。故障诊断博弈的流程如图1所示。

图1 故障诊断博弈模型流程Fig.1 Fault Diagnosis Game Model Flow
旋转机械的振动信号包含足够的故障信息。作为强化学习中的关键要素,代理对环境和状态的有效感知至关重要。对于诸如Q学习的原始强化学习方法,由于这些方法表示状态的能力有限,所以仅基于振动信号很难区分和识别旋转机械的状态。考虑SAE提取滚动轴承的故障特征中的广泛应用,因此在这里中使用了堆叠自动编码器DNN来感知振动信号中存在的故障信息。在提出的方法中,DQN代理的构建是通过顺序堆叠获得的编码器,再使用存储在SAE的预训练中的权重初始化参数,并添加线性层以将SAE的输出映射到Q值。与基于CNN的特征提取方法不同,SAE采用完全连接的模型进行逐级内在特征学习。
SAE可以有效提取故障特征有两个重要原因。首先是SAE可以通过逐层自学学习原始信号的表示。第二个原因是稀疏约束可以通过限制每个自动编码器的参数空间来防止过度拟合。这里中使用的SAE在输入层和输出Q值层之间有两个隐藏层。且使用的SAE体系结构保持不变。每个编码器的激活函数是一个整流线性单位(ReLU),并且应用于编码器的正则化方法是L1正则化方法,这意味着如果神经网络中的参数的绝对值过大也会受到惩罚[15]。在训练DRL方法之前,将预训练方法应用于所有训练数据样本上的自动编码器。然后,提取自动编码器,并通过堆叠输入层、所有训练有素的编码器以及用于输出Q值的完全连接层来构建代理的感知部分。
对于掌握博弈的代理,单个观察状态包含多个博弈模型。因此,从博弈中观察到的状态不是独立的,而是分布均匀的。对于旋转机械的故障诊断,由于振动信号的周期性,样本可被视为独立且分布均匀的样本。考虑到上述差异,本研究中对代理的观察由单个故障样本组成。此外,Bellman方程中的衰减因子等于零,这意味着不考虑当前状态下的历史经验。
算法1中说明了用于训练基于SAE的DQN的算法。训练过程包括两个单独的部分。第一个是SAE的预培训,第二个是DQN代理的培训。代理根据ε-贪婪策略选择并执行动作,这意味着该动作是基于概率ε随机选择的,并且对应于最大q值的动作是由概率1-ε选择的。本研究中使用的优化算法是适应矩优化。
虽然已经完成了代理的训炼过程,但是代理只能输出动作的Q值,而不能给出诊断结果,所以代理仍不能用于诊断滚动轴承故障。因此,代理的输出层需要确定Q值的最大值,然后输出相应的操作,才能够获得诊断旋转机械故障的代理。此时,在训练和测试过程中,输入数据均为原始振动信号。即这里使用的方法实现了端到端故障诊断。完整方法的流程图,如图2所示。

图2 所提出方法的流程图Fig.2 Flow Chart of the Proposed Method
4 故障诊断实例
4.1 案例1:滚动轴承的故障诊断
这里中使用的滚动轴承的故障数据是来源于凯斯西储大学轴承失效实验[16]。该数据集包括正常轴承和故障轴承的滚动轴承测试数据。实验的动力产生器是两马力的电动机,振动数据是从驱动端收集的加速度数据,在电动机轴承的近端测量的采样频率为48 kHz。滚动轴承故障注入的实验设备,如图3所示。按轴承振动信号特点分故障形式一般可以分为表面损伤和磨损类损伤。轴承在使用过程中,通常会产生低频和高频段的振动信号。低频信号是由于轴承元件的工作表面损伤点在运行中反复撞击与之相接触的其它元件表面而产生的,也称“通过振动”。损伤发生在内、外圈或滚动体上时,这个振动发生的频率是不同的,称其为故障特征频率。带缺陷的滚动轴承元件在运行中的特征频率一般出现在1kHz以下,是滚动轴承故障的重要特征信息之一。收集了四个条件下的数据,包括一个正常条件(N)和三个故障条件(F)。故障条件是外圈故障(OF)、内圈故障(IF)和滚轴故障(RF)。另外,引入滚动轴承的故障都是单点故障。此外,故障直径的受损程度不同,包括0.007英寸、0.014英寸、0.021英寸和0.028英寸。
为了验证该方法的有效性,根据载荷将振动数据分为四组(S1、S2、S3和S4)。每组包含十种故障模式,根据故障直径和故障位置划分。S1、S2和S3分别包含一个马力、两个马力和三个马力负载下的所有故障模式。每个故障集有12,000个样本,每个样本包含400个数据点。数据集都是未经预处理的原始振动信号。S4是S1、S2和S3的并集,它在所有负载下都有36,000个样本。
在训练过程中,SAE网络具有四层,包括一个输入层,两个训练过的编码器和一个输出层。输入样本的维数决定输入层的单位数,第一个编码器和第个二编码器的单位数分别为128和32,Q值的维数决定输出层的单位数。编码器中使用的激活函数是ReLU,反向传播函数使用的是Adam。此外,还利用防止过度拟合并提高训练效率的L1正则化来约束、限制神经单位权重的参数空间。每个自动编码器的最大训练时期为200,DQN代理的训练时期为2000,每个时期包含512轮诊断博弈。DQN代理的重放记忆大小为64。重放记忆是从记忆中随机选择的样本,用于将DQN代理训练为小批量。因此,本次研究的最小批量大小为64。为了测试和验证所提出方法的性能,将十倍交叉验证应用于四个数据集,每十轮计算奖励的平均值。如图3所示DQN代理在训练过程中的进度曲线。此外,诊断后的结果总结在图4中。
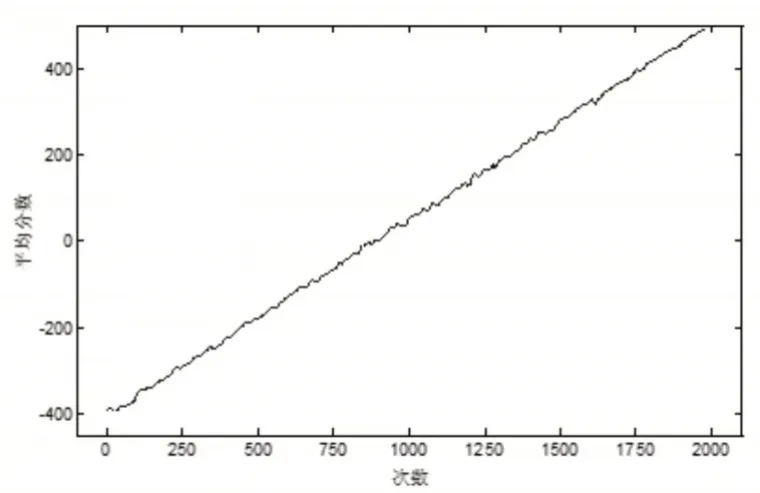
图3 代理在滚动轴承数据集故障诊断训练过程中的分数Fig.3 Score of Agent in Rolling Bearing Data Set Fault Diagnosis Training
故障诊断代理为正确答案时得一分,为错误答案时减一分,这意味着在512轮博弈中,总得分在(-512)到512点之间。在博弈开始时,由于缺乏任何先验知识和经验作为参考,DQN代理处于随机猜测阶段。由于故障诊断结果具有十个类别,所以代理获得正确答案的概率只有0.1。因此,在开始时,得分约为(-460)分。随着培训过程的进行,代理将从自己的历史经验和分数变化中学习。如图4所示,分数随着训练而增加,并且在接近最后时期时达到近512分。上述提到的分数与奖励相同,它们被用作评估代理性能的反馈。通过每个时期的总奖励可以来观察DQN代理向全局极值的收敛,因为诊断的准确性直接反映在总奖励上。当总奖励足够高并开始振荡时,可以认为DQN代理的训练过程已完成。

图4 滚动轴承数据集的十倍交叉验证的诊断结果Fig.4 Diagnosis Results of Ten Fold Cross Validation of Rolling Bearing Data Set
图5 说明受过训练的代理可以在多种情况下有效地诊断故障。十倍交叉验证的定量结果显示在表1中。为了说明所提出方法的性能和有效性,还使用基于监督学习训练的SAE模型,通过十倍交叉验证来处理相同的数据集。输入层和两个自动编码器与DQN代理的相应层相同。输出层有十个节点,并使用softmax函数输出分类结果。该模型的训练过程包括自动编码器的逐层预训练和整个SAE模型的微调。总体而言,两种方法均达到了很好的诊断准确性和稳定性。在训练集上,所提出的方法能够以接近100%的准确度正确区分样本,而SAE-Softmax方法可以正确区分所有样本。在测试集上,这两种方法的准确性和相应的标准偏差非常接近。计算数据集S1、S2、S3和S4的两种方法之间差异的绝对值分别为0.0069、0.012、0.0126和0.0075。考虑到基于监督学习的方法在确认样本及其对应标签之间的关系方面具有优势,因此该结果说明了所提出方法的有效性。另外,测试精度的最大标准偏差为0.0144,这表明该方法可以对故障样本进行稳定的分类。
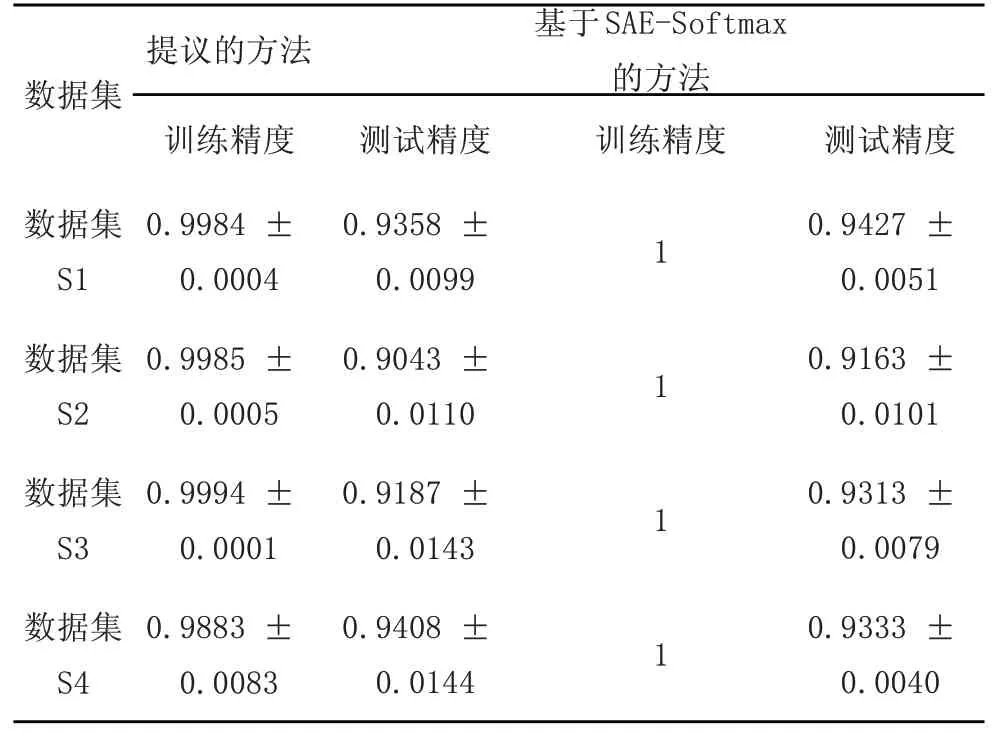
表1 滚动轴承数据集的诊断结果(平均准确度±标准偏差)Tab.1 Diagnosis Results of Rolling Bearing Data Set(Average Accuracy±Standard Deviation)
具体来说,数据集S4的情况是四个数据集中最复杂的,它包含三个不同负载下十种健康状况的原始振动信号。所提出的方法能够在工作条件下区分故障模式。而除了在数据集S4上进行测试的平均准确度之外,SAE-Softmax方法在所有实验中的性能均优于所提出的方法。总之,结果表明,所提出的方法可以训练基于DNN的代理学习如何仅使用原始振动信号来诊断滚动轴承的故障,而与故障类别、严重性和工作条件无关。这里使用的SAE模型可以感知原始振动信号,并且是端到端故障诊断方法的前端。为了进一步了解代理如何学习诊断故障并验证代理挖掘故障特征的能力,利用t分布随机邻域嵌入(t-distributed stochastic neighbor embedding,t-DSNE)来对DQN代理内部的SAE模型的输出进行可视化[17]。第二个编码器的输出被视为代理学习到的特征,因为DQN代理的输出层是一个输出Q值的线性层。因此,在案例1中,从单个样本中提取的特征向量的维数为32。t-DSNE算法应用于高维特征,数据集S1-S4的可视化结果如图5所示。具有相同健康状况的样本以曲线或圆形区域的形状聚集在一起,并且具有不同健康状况的样本之间存在明显的边界。通过可视化DQN代理的感知部分获得的原始振动信号的表示,所提出的基于DRL的故障诊断方法可以提取故障特征并相应地识别故障。

图5 滚动轴承数据集最后一个隐藏层中的t-SNEFig.5 T-SNE In the Last Hidden Layer of Rolling Bearing Dataset
4.2 案例2:液压泵故障诊断
案例2中使用的液压泵数据是从7个燃油输送泵中收集的。包含两个常见的故障,即滑动件松动和阀板磨损,已被物理式地注入泵中。液压泵的振动信号由加速度传感器从泵的端面获取,并具有528 rpm的稳定电机速度和1024 Hz的采样率。每个泵收集了两个样本,每个样本包含1024个点,总共收集了14个样本。由于对数据集使用了十倍交叉验证进行验证,因此进行了十次试验,其中随机选择了10%的样本进行测试,选择了90%的样本进行了训练。针对案例2,提出的方法性能通过十倍交叉验证的相应偏差的平均精度来进行评估。
如图6所示,代理程序每十次迭代的平均回报趋势。由于案例2包含泵的三种健康状态,代理可以得出三分之一的正确答案。因此,即使分数在开始时约为-314,但随着训练过程的进行,分数增加到512分。表2显示了十次交叉验证的平均准确度和相应的标准差。训练和测试的平均准确度均为100%,这意味着所提出的方法可以正确分类每种故障模式的样本。与案例1相似,使用SAE-Softmax模型来诊断故障,其诊断结果比所提出的方法稍差。考虑到将严重故障注入液压泵核心部件的安全隐患,故障模式和严重性的变化并不像案例1那样复杂。但是,信号是从7个不同的泵中收集的,并且传感器的采样率远低于案例1。因此,案例2从三个角度说明了所提出方法在多个设备、样本相对较少的条件下能够实现对旋转机械故障进行有效诊断。结果表明,所提出的方法和基于SAE-Softmax的方法都可以利用有限振动信号的持续而有效地对不同液压泵的状态进行分类。这说明所提出的方法具有从原始传感信号中挖掘与故障模式相关的特征的能力。

表2 泵数据集的诊断结果Tab.2 Diagnosis Results of Pump Data Set

图6 液压泵数据集的代理分数Fig.6 Proxy Score of Hydraulic Pump Data Set
同样,为了可视化该方法从原始数据中自主学习的功能,继续使用t-DSNE呈现所学习的DQN代理的低维表示。如图7所示,通过t-DSNE减小了DQN代理提取的特征的维数,这样便于可视化。可以看到,不同健康状况的散布点彼此分开。但是,相同健康状况的散布点被聚集成几个小聚类,而不是被均匀地聚集成一个聚类。这是因为在DQN内部的SAE中添加了稀疏限制后,具有相同健康状况但有少许差异的样本可能会导致不同位置的神经元被激活。这会导致高维空间中的特征彼此相距较远。但是激活的神经元都与相同的输出相关,即它们仍然可以被归为同一类别。综合来看,基于SAE的原始信号感知和基于DQN的自学式体验学习的结合是所提出的方法能够取得如此优异效果的关键原因。
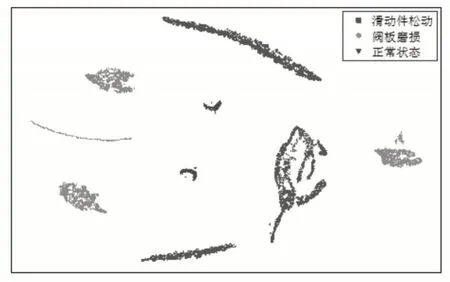
图7 液压泵数据最后一个隐藏层中的t-SNEFig.7 T-SNE In the last Hidden Layer of Hydraulic Pump Data
案例研究表明,提出的方法和基于SAE-Softmax的方法都可以对旋转机械的健康状态进行分类。但是,考虑到训练过程中的时间消耗,这些方法是不同的。对于提出的方法,算法的运行时间取决于代理的学习曲线时间。具体来说,对于案例1和案例2,代理都需要2000个时间点才能获得近512分的高分。此外,无论训练集中的样本数量如何,每个时期的时间都是相同的。对于基于监督学习的SAE-Softmax方法,训练过程的运行时间与训练集中的样本数量成正相关。由于这里提出的方法用于故障诊断的学习方法是自我探索的,因此该方法的运行时间比基于SAE-Softmax方法的运行时间更长。但是,考虑到监督学习算法前期需要储备的先验知识,提出方法的效率超过基于监督学习的深度学习方法。
5 结论
这里提出了一种一种基于堆叠式自动编码器与深度Q网络相结合的深度强化学习旋转机械故障诊断方法,使用滚动轴承和液压泵数据集对该方法进行实验验证,可得出如下结论:
(1)通过结合强化学习的自主学习能力和深度学习的感知能力,提出的基于深度强化学习的方法可以实现旋转机械端到端故障诊断方法。在保证了诊断精度与可靠性的前提下,该方法大大减少了对故障诊断的先验知识和专家经验的依赖。
(2)通过设计故障诊断博弈环境,该方法可以成功地使用DRL获得智能故障诊断代理。能够有效建立无监督诊断模型,并且有较好的诊断效果。
(3)故障诊断代理受益于记忆回放和基于奖励的反馈机制,仅基于弱反馈就能够了解不同故障模式与原始振动信号之间的非线性映射关系,为旋转机械的故障诊断问题提供了一种更通用和智能的解决方案的方法和思想。
