空气静压轴承气旋机理及其影响因素分析

唐璐阳，张小龙，寇 盼

（西安建筑科技大学机电工程学院，陕西 西安710055）

1 引言

空气静压电主轴以空气静压轴承支承、以电机或者涡轮为动力驱动，带动刀具高速旋转，从而实现高速精密加工，具有回转精度高、低振动、转速高等特点，在机床、精密仪器、医疗器械等领域均得到广泛应用［1］。

作为超精密加工的重要部件，空气静压轴承的性能影响着被加工精密零件的质量［2］。近几年来，关于空气静压轴承的微振动现象已有很多研究成果。文献［3］通过实验发现了气体通过供气孔进入轴承气膜时具有明显的压力降现象。文献［4］通过对超精密气浮工作台的振动特性分析，发现了高速气体通过有腔节流孔时产生“气旋”现象，会导致气膜波动。文献［5］利用Star-CD软件仿真了S型和R型节流孔的内部气体流动情况，并通过实验验证了不同节流孔形状对轴承微振动有影响。文献［6］进一步研究了S型和R型节流孔对轴承承载力和稳定性的影响。为了抑制微振动提高加工精度，文献［7］实验研究发现了增加均压槽可降低轴承微振动80%左右，能显著提高轴承的稳定性。文献［8］研究认为由于空气轴承节流孔内气流雷诺数过大而导致了微振动，并提出了减小微振动的方法。文献［9］和文献O［10］考虑是边界区和惯性区、激波与边界层的相互作用，在供气压力较高和气膜间隙较大的条件下，发现在节流孔入口和出口转角处存在激波现象，从而导致气膜温度和压力下降，甚至使节流孔内的气体流动由层流向湍流转化，使轴承出现微振动。

针对上述研究，目前研究认为节流孔压力腔内气体流动的非均匀性引起的“气旋”现象是轴承微振动的主要原因［11］，研究相对集中在求解气旋稳态特性下不同工艺参数和几何参数对气旋的影响，但以上研究对气旋瞬态发展过程和微振动的产生机制研究相对较少。利用STAR-ccm+软件对节流孔内气旋的产生及其瞬态变化情况进行模拟，确定了气旋导致微振动的产生机制、并从稳态和瞬态两方面研究了不同轴承供气压力和压力腔形状对气旋强度的影响，为空气静压轴承的设计提供理论依据。

2 气旋及其对微振动的作用

2.1 大涡模拟

为了模拟节流孔内流体的动态变化情况，这里利用这里进行大涡模拟时，我们利用STAR-ccm+中的大涡模拟进行节流孔内流场的瞬态求解，STAR-ccm+可以更加清楚获得流场内的分布情况，使用方便高效，以其稳健精确的数值算法、覆盖面广的理论模型以及易处理的网格体系，是一款优秀的CFD模拟软件，是新一代CFD软件的最强闪光点［12］。

大涡模拟［13］将湍流瞬时脉动分解为直接模拟大尺度脉动和输送方程模拟小尺度脉动，大尺度脉动通过N～S方程直接求解，而小尺度脉动通过亚格力应力模型来求解，计算量相比直接模拟较小，模型比较容易构造，能够捕捉到雷诺平均法无法得到的许多非稳态和非平稳过程中的湍流过程。通过大涡模拟能精确求解节流孔内流体的瞬时流动情况，便于分析气旋以及微振动的机理。

利用大涡模拟时采用的节流孔形状及计算域如图1所示。节流孔是空气静压设计的关键，节流孔的直径一般在（0.1～1.0）mm［14］，且计算域主要几何尺寸分别为节流孔直径d=0.24 mm，气膜厚度h0=0.013mm，节流孔深度l=1mm，压力腔宽度B=2mm，压力腔深度H=0.1mm。且气膜间隙区域的上边界与轴承内表面相接触，气膜区域的下边界与主轴表面相接触。另外在分析时节省时间，只取计算域模型的1/4进行分析。

图1 计算域模型图Fig.1 Computational Domain Model Diagram

利用STAR-ccm+进行大涡模拟时，将雷诺平均法的稳态计算值作为大涡模拟的计算初始值，这样保证为大涡模拟提供准确的初始流场以减少计算时间。这里我们将雷诺平均法的稳态计算值作为大涡模拟的计算初始值，可以为大涡模拟提供准确的初始流场以减少计算时间。流场计算域采用六面体结构进行网格划分，进气口供气压力为0.435MPa，出气口供气压力为0.1MPa。Model选择PISO非稳态计算，Turbulence选择大漩涡模拟，选择气体动力粘度属性为Sutherland定律，本次大涡模拟选用WALE模型来模拟节流孔湍流数值计算，设置WALE模型常数Cw为0.325。由于大涡模拟为非定常计算，在时间离散上采用二阶隐式模型，设置迭代时间步长Δt为10-7s，时间步长的选择要满足CFL条件，即：

式中：μ-流经网格单元的流体速度大小，m/s；Δx-速度方向上的最小网格尺寸，m；Δt-迭代时间步长。单个时间步长内迭代20次，最后根据收敛情况适当调整亚松弛因子保证残差收敛。

由于实际节流孔内气体流动是非常复杂的，因此我们需要做以下简单假设：（1）运动环境温度为恒温过程；（2）设气膜厚度h0为常值；（3）在气膜区域内垂直于轴承间隙的压力和密度相等。

2.2 气旋及微振动

节流孔段类似于拉伐尔喷管［15］，从节流孔进气口区域供入的气体喷射到较大的自由空间，这部分气体流动恰好为流体的冲击射流，冲击射流的示意图，如图2所示，气流流动按照特征可以分为自由射流区、阻滞区以及壁面射流区。

图2 冲击射流二维示意图Fig.2 Two-dimensional Schematic Diagram of Impinging Jets

相比自由射流区、阻滞区以及壁面射流区，为了详细分析节流孔内流场分布情况，根据节流孔形状和气体流动情况，把流场计算域分为四个不同区域，如图3所示。

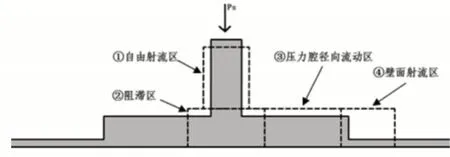
图3 内部流场过程示意图Fig.3 Internal Fow Field Process Diagram

处于进气口下的①自由射流区，射流的边界接触着节流孔壁面，环境流体与射流边界之间的相互剪切作用，从而使动能、能量在发生空吸作用，空吸作用使得射流内径向速度的分布发生变化。气流将沿①区域保持高速向下流动。

当气流到达②阻滞区域，气流流线发生弯曲，气流产生回流和分离，从而导致气流紊乱，形成了湍流效应，湍动能强度较大。垂直气流开始接触到主轴表面，气流轴向速度急剧减少且速度方向改变90°，导致气体速度梯度的产生，对比图3中的速度云图可以清楚看到产生速度梯度的区域大约是②区域中的2d范围内。

在空吸作用下，气体与周围的静止气体相接触形成了气旋，此时形成气旋的强度较大，气旋的中心处是压力最低的地方，气旋边缘与中心产生的压力差推动气旋运动，气旋运动的气旋受到周围气体的粘性作用，使得气旋强度逐渐减少，随着从①自由射流区域气体的不断输入，气旋不断的生成和破裂，从而引起剧烈的压力波动，导致轴承的微振动最大。图4是利用大涡模拟得到压力腔内部的瞬时流态图，可以看到气旋生成到破裂消散的过程。

图4 不同时刻压力腔的流场速度和压力云图Fig.4 Flow Field transient Velocity and Pressure Cloud Diagram of the Pressure Chamber

在进入壁面射流区之前，气流首先要沿压力腔径向位置流动，气流会与压力腔壁面发生碰撞，继续又在压力腔内产生气旋，但相比在②阻滞区域，气旋强度较小，产生的气旋影响压力腔内压力波动，持续对轴承微振动产生影响。

气流经过壁面射流区时，气流总体方向沿径向向外流动，各个方向上的气流在压力腔出口处相汇合，共同从压力腔出口流入气膜区域，当从压力腔出口流向气膜区域时，气流流动区域面积由厘米变至微米级别，造成动能增强，各个方向上的速度在压力腔出口处形成湍流，形成的湍动能强度和压力波动相比②阻滞区域较小，也会对轴承微振动产生影响。在气膜区域流动的气体沿轴向流动，气流主要受主轴-轴承壁面的摩擦力作用，在摩擦力的作用下气流速度越来越小，流动状态为层流，对轴承的微振动几乎没有影响。

另外，分析不同时刻下计算域的瞬时涡量分布图，气体在①自由射流区域高速向下流动时，这部分气体包含有极大的能量，由于不存在空吸作用，此时的涡量为零；当气流抵达②阻滞区域，在“2d”范围内最先形成气旋，此处的涡量较大，对比图5（a）-（c）过程可以看出节流孔出口形成的气旋在径向速度的驱动下，沿径向开始移动，但是受气流粘性作用，空吸作用变弱可以看到气旋强度明显减小，从涡量分布图可以看出涡量有所减少。在压力腔内由于运动气流和压力腔壁面产生碰撞，又有气旋的产生，压力腔内气旋持续影响气膜压力波动。从图5（d）看到，涡量在压力腔出口处集中，压力和速度波动对轴承微振动产生影响。

图5 不同时刻下计算域的涡量分布云图Fig.5 Transient Vorticity Distribution Cloud Map of the Computational Domain

最后进入气膜区域的气体沿轴向流动，气流受摩擦力作用速度越来越小，不会产生气旋，涡量逐渐减为零。通过以上对气体在节流孔内的流动情况分析，导致轴承产生微振动主要有以下几方面：（1）从冲量角度来讲；气旋与压力腔不平行且垂直的速度分量会导致主轴-轴承微振动；（2）从压力变化来讲；气旋造成压力降产生压力脉动，这种压力脉动作用在主轴表面产生微振动；（3）在壁面射流区各个方向的气流在压力腔出口处汇聚，这种不稳定的气流形态造成湍动能的增加而导致微振动。另外空气静压主轴在运转时，主要的内部热源为空气静压轴承的摩擦生热［16］。因为下气膜与运转中的高速主轴相接触，气膜上下边界之间形成较大的速度梯度，从而产生大量的剪切摩擦热，这些剪切摩擦热会导致主轴热变形，进而影响气膜间隙，造成气膜压力波动。

3 影响气旋的因素分析

气旋是轴承微振动的主要原因，影响气旋的因素主要由结构几何参数和工艺参数两部分构成，这里对不同供气压力和压力腔形状的稳态和瞬态特性进行分析。

3.1 不同供气压力下的稳态分析

供气压力的大小严重影响轴承的工作性能，适当增加供气压力可以增加轴承的承载力和刚度，但是当供气压力过大时，可能导致轴承工作不稳定，增加轴承气锤振动发生的可能性。为防止出现“气锤”现象，仿真了供气压力分别等于0.335MPa和0.535MPa两种情况下节流孔的稳态内部流场。并用压力降大小和湍动能大小表示气旋强度大小。

通过绘制不同供气压力下节流孔对称中心沿径向位置的压力和湍动能变化曲线，从图6压力分大小分布曲线图可以看出气旋的中心为曲线的最低点，当供气压力为0.335MPa时，气旋导致的压力降为9134Pa；当供气压力为0.535MPa时，气旋导致的压力降分别为20181Pa。因此随着供气压力的增加，气旋导致的压力降增大。从图7湍动能大小分布曲线图可以看出供气压力越大，湍动能越大，引起轴承的微振动越大。

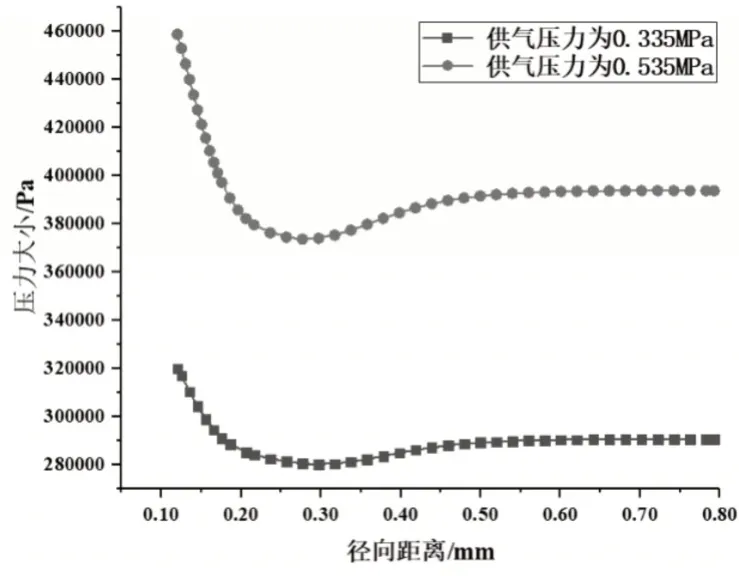
图6 不同供气压力下压力沿径向位置分布曲线图Fig.6 Distribution Curve of Pressure Along Radial Position Under Different Air Supply Pressure

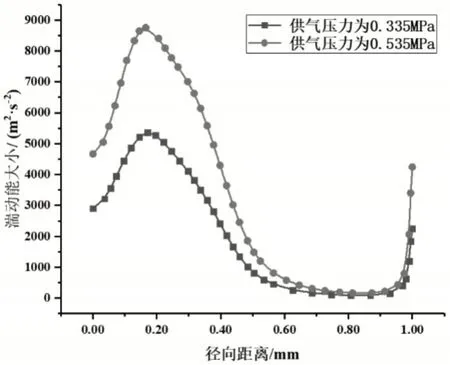
图7 不同供气压力下湍动能沿径向位置分布曲线图Fig.7 Distribution Curve of Turbulent Kinetic Energy Along Radial Position under Different Air Supply Pressure

3.2 不同供气压力下的瞬态分析

如图8所示，为不同供气压力下的计算域瞬态速度和压力云图，不同时刻下，另外观察瞬态下的计算域气流流态情况，可以看到气旋形成到消散的过程，在节流孔出口处的气旋强度最大，沿着压力腔径向位置气旋强度逐渐减少，引起的压力波动逐渐减少，这里同2.2节的分析是一致的。在供气压力更大的情况下，气旋强度逐渐增大。随着供气压力增大，气旋首先形成的位置差别不大，但是气旋所在区域的中心与边缘速度差、压力差明显增大，且供气压力的增大，输入系统的能量增加，在气腔结构不变的情况下，气体的流动状态变得紊乱，气体的最大流速逐渐增大。

图8 不同供气压力下的瞬态速度和压力云图Fig.8 Transient Speed and Pressure Cloud Diagrams at Different Supply Pressures

3.3 不同压力腔形状下的稳态分析

为了研究不同压力腔形状对气旋的影响规律，选用如图9所示的压力腔模型，两种模型仅压力腔形状不同，其具体形状和参数如图所示。

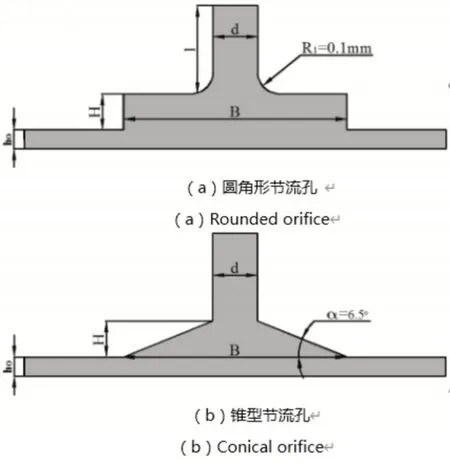
图9 压力腔模型Fig.9 Pressure Chamber Model

通过绘制不同压力腔形状下节流孔对称中心沿径向位置的压力和湍动能变化曲线，如图10所示，两种压力腔内都有气旋的产生，锥形压力腔内的气旋所造成的压力降明显最大，且气旋面积相比更广。而圆角压力腔起到了过渡缓冲的作用，不仅减缓压力腔内的速度增加，而且也能降低压力降的大小。

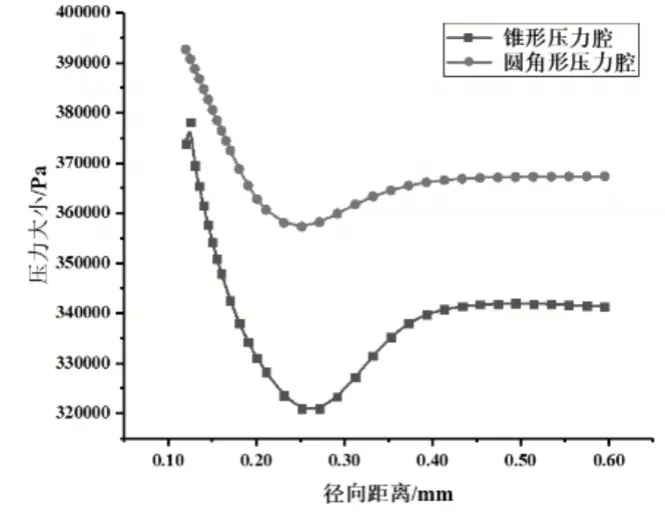
图10 不同压力腔形状压力沿径向位置分布曲线图Fig.10 Distribution Curve of Pressure Along Radial Pposition under Different Pressure Chamber Shape

不同压力腔形状时的流体的湍动能分布曲线，如图11所示。可以看到圆角节流孔的湍动能在沿压力腔径向分布中明显最小，锥形节流孔产生的能量积聚对压力腔垂直面产生的冲击更大，气旋强度更大。

图11 不同压力腔形状湍动能沿径向位置分布曲线图Fig.11 Distribution Curve of Turbulent Kinetic Energy Along Radial Position under Different Pressure Chamber Shape

3.4 不同压力腔形状下的瞬态分析

通过对比圆角形和锥形压力腔的不同时刻速度分布图，如图12所示可以看到圆角压力腔由于圆角的存在在节流孔处的气流过渡效果总是优于锥形压力腔。且锥形压力腔内气旋形成面积区域大于圆角气旋形成面积区域。且圆角压力腔的最大气流速度明显小于锥形压力腔的最大气流速度。

图12 不同压力腔形状的瞬态速度云图Fig.12 Transient Speed Cloud Diagrams at Different Pressure Chamber Shape

通过对比稳态和瞬态的仿真结果，因此在压力腔的设计过程中，选择合适的弧度进行过渡，一方面可以减少阻力，另一方面可以使气体流动更加通畅，减小气旋强度降低微振动。

4 结论

利用STAR-ccm+软件对空气静压轴承的内部流场进行了仿真分析，得到以下主要结论：（1）通过利用冲击射流的气流流动结构特征划分了气流流场区域，利用大涡模拟研究了不同区域的气流瞬时流动情况，研究了气旋的产生和变化规律。（2）从冲量原理、压力变化等方面确定了气旋导致微振动的机理，即产生于阻滞区域、压力腔径向流动区的气旋以及在壁面射流区中的压力腔出口处形成湍动能和压力波动。（3）数值分析对比不了同供气压力和不同压力腔形状下计算域稳态和瞬态流场，理论分析结合仿真结果表明，随着供气压力的增加，气旋强度增加，不同形状的压力腔对气旋强度影响也较大。因此通过数值模拟气旋强度，可以选择较优的压力腔形状。