α-Shape算法双机器人协作工作空间研究

朱良麒，丁力平，陈文亮，周志光

（1.南京航空航天大学机电工程学院，江苏 南京210016；2.江苏雷利电机股份有限公司 工程中心，江苏 常州213011）

1 引言

机器人工作空间是指机器人末端坐标系的原点在空间中所能到达的区域［1］，是衡量机器人工作能力的重要运动学指标之一［2］，而双机器人协作工作空间是指参与协作的机器人的工作空间所形成的交集［3］。工作空间与协作工作空间在机器人的机构设计、安装布局、路径规划、避碰、机器视觉和最佳操作位形等研究方面有着非常重要的参考意义，是当下机器人领域的研究热点，但同时也是技术难点。

研究和分析机器人协作工作空间是提高机器人协作效率和确保其安全生产的关键。目前为止，国内外学者在双机器人协作工作空间问题求解上采用的方法与单个机器人工作空间求解方法类似，主要有：几何图解法、解析法和数值法［4］。尤其是近年来随着电子计算机技术的发展，蒙特卡洛数值方法［5］在机器人工作空间的求解上得到了广泛应用，并且同时也比较适合分析协作工作空间，该方法不涉及逆运动学求解，算法相对较简单，具有较强的通用性。但这种方法生成的工作空间点云集只是对实际工作空间的一种近似表示，无法为工程实践提供较为具体的数值分析。因此很多学者将研究目标集中在由工作空间点云获得工作空间曲面的方法寻求上［6～8］，其主要工作一般是对工作空间点云分层，再逐层提取边界点，并拟合为边界曲线，最后求出工作空间包络曲面。该方法求解过程中边界点提取以及包络线求解较复杂，且通用性不强，更难对协作工作空间进行求解。

为了使工作空间可视化和数字化，提高应用性，范启忠等［9］运用了a-Shape算法处理单个机器人工作空间点云，对工作空间进行三维重建，并通过调整a参数大小得到了较高的重建精度，该方法具有较好通用性。基于此，这里进行更深入的研究，通过一定算法获取双机器人协作工作空间的点云后，运用a-Shape算法分别对机器人工作空间以及协作工作空间进行重建，更加突显该算法的优越性，对机器人协作技术奠定了基础。

2 协作工作空间定义及点云获取

2.1 双机器人协作工作空间定义

一般情况下，我们将参与协同作业的两个机器人分别设置为主、从机器人，由机器人运动学关系可知，其TCP点位置矢量与关节位移存在一一对应的函数关系，可表示为：

式中：q-关节变量；p-位置矢量；下标m、s-主机器人与从机器人，函数f与g由机器人正运动学得出。

为了简化计算，实际中一般选取世界坐标系Fw与主机器人基坐标系一致。则主机器人工作空间可表示为：

从机器人在其基坐标系Fbs下的工作空间可表示为：

故双机器人协作工作空间可表示为：

公式（3）～（6）用集合形式定义了机器人的工作空间与协作工作空间，其解集应是连续的，但这种表达形式不直观，解析过程太复杂，难以直接运用。

2.2 蒙特卡罗法机器人工作空间点云模型

蒙特卡罗法的思想是通过大量随机样本，对系统的特性进行模拟，进而得到问题的近似解。对机器人工作空间建立起随机概率模型，将末端TCP点的空间位置看做随机数，当随机样本足够大时，这些随机点构成的区域就近似代表了机器人的工作空间。因此，在关节空间内随机产生大量组关节位移q，通过一映射得到末端坐标系原点的位置随机点，这些点的集合就可以表示为机器人工作空间的离散模型，具体计算步骤如下：

（1）在各关节变量范围［qimin，qimax］内取随机值，得到N组关节矢量；（2）进行机器人正运动学方程推导，并将上一步得到的N组关节矢量带入，得到对应的N个末端TCP点即随机点；（3）利用计算机的绘图功能将所有随机点以描点的方式显示，得到工作空间的点云图。

2.3 协作工作空间点云获取

获取协作工作空间的点云图，最简单直接的方法是求解主、从机器人点云集的交集，找出重合的点。但由于点运数据是离散的，这种方法只能搜索到极少部分的点，忽略了处于协作工作空间内而没有相互重合的点。如图1所示，方形点表示主机器人的随机点，圆形点表示从机器人的随机点，可以看到大多数的点位于“协作区”却不能按照求交集的方法寻到，误差过大。

图1 协作区域随机点分布示意图Fig.1 Schematic Diagram of Random Point Distribution in the Collaboration Area

为了获得更多的协作工作空间点，可以采取计算点与点距离并加入一定阈值的判断方法：遍历主机器人点云集的每个随机点再依次计算该点与从机器人点云集的随机点的距离，设置允许的阈值为e，若存在满足的两点，则认为pm、ps就是协作工作空间点，待遍历完成后，就获得了协作工作空间的原始点云数据。该方法可以提取到大部分位于协作区域而没有相互重合的点。获得双机器人协作工作空间的离散模型即点云集后，可以通过绘图方式粗略地看到点云的大体分布情况。

3 α-Shape算法工作空间轮廓提取

3.1 α-Shape算法原理

文献［9］第一次给出了面向点云数据α-Shape的通用概念，并给出了α-Shape族的一种计算方法α-Shape。算法可以从一堆无序离散点集中提取边缘，并通过一定的算法获得重建的图形，平面点云的α-Shape为一个多边形，三维空间点云集的α-Shape则是一个多面体。R2空间中，其原理如图2所示，设S为一有限无序点集，α为（0，∞）范围内的实数，假想一个半径为α的圆在点集S外滚动，若α足够大时，这个圆就不会掉进点与点之间的空隙，滚落到点集内部，其滚动的痕迹便是该点集的边界线。

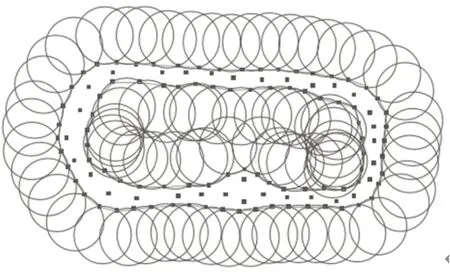
图2 α-Shape算法原理图Fig.2 Schematic Diagram of α-Shape Algorithm

具体的判别方法可以描述为：点集S由n个点构成，n个点组成n*（n-1）条线段，过点集S中任意两点P1、P2作半径为α的圆（一般可以得到两个圆），如果有一个圆内部不包含点集S中的其他任何点，就认为P1、P2是边界点，其连线为边界线段。所以，当α值非常小时，则每个点都在边界上；若α很大（α→∞）时，则形成的边界线为点集S的凸包［10］。

同理，R3空间中的α-Shape算法则是通过点集S中的三点作半径为α的球来判别边界点，并在得到的边界点处建立三角片面，以三角片面的形式重构出曲面。重构结果随着α取值的不同而变化，α值偏大会保留更多的三角面片，表现为点集的凸包，α值偏小则会出现空洞，α为0时，α-Shape退化为原始的点集［11］。

3.2 基于形体体积值的参数α确定

α-Shape算法直观的表达了点云集的形状，同时其精细程度由α控制。因此，为了获得理想的三维重构效果，需要确定出合适的参数α值。理论上，多自由度关节型机器人的工作空间类似球状，受各关节转动范围限制和奇异性等因素的影响，空间分布会有所变化，其点云的三维重构结果表现为一定形体的封闭空间。因此，可以考虑将形体的体积计算值作为参考衡量重构效果。这里基于MATLAB volume（）函数对建立的三维α-Shape形状体积进行求解，计算大量组不同参数ai下对应的多面体体积值Vi，将结果以坐标（ai，Vi）的形式记录，得到体积随参数变化的趋势关系，进而根据三维α-Shape形状特点分析并确定参数a的值。

4 实例分析与验证

以两台ABB公司的IRB140型6轴多用途工业机器人为例，对文中方法进行验证。该型机器人的实物图如图3所示，采用DH法［12］建立连杆坐标系，结果如图4所示，相应的连杆参数如表1所示。机器人正运动方程可以表示为：

图3 IRB140机器人实物Fig.3 The Object of IRB140 Robot

图4 机器人连杆坐标系Fig.4 Robot Link Coordinate System

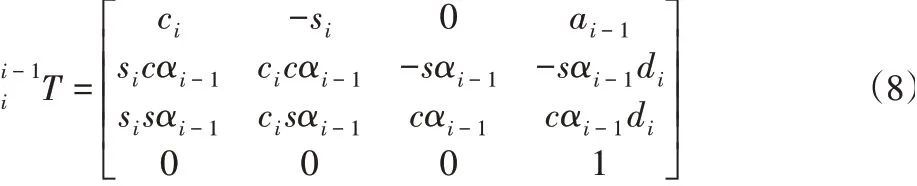
考虑末端安装有法兰，主从机器人实际的TCP点坐标系到各自基坐标系的总变换为：

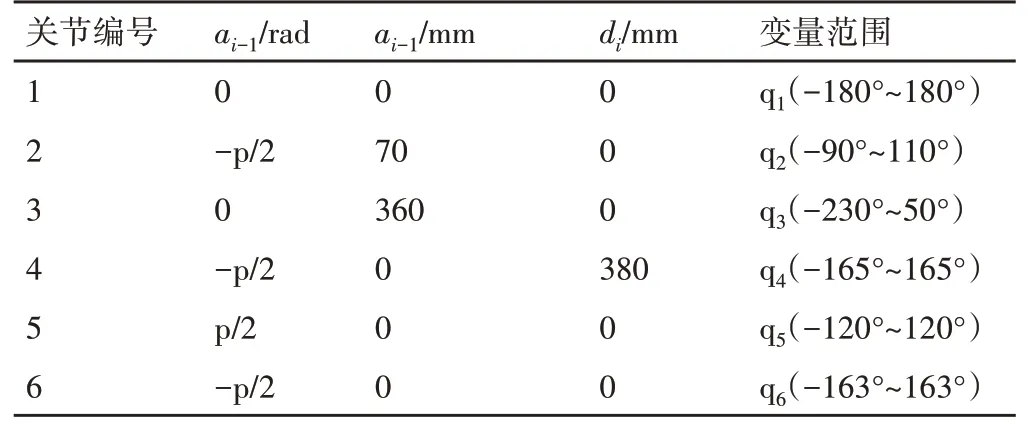
表1 IRB140机器人D-H参数Tab.1 The D-H Parameters of IRB140 Robot

为便于从机器人工作空间计算，设两台机器人采取典型的地面式-地面式且两者相对的安装方式，基坐标系原点之间距离为1.2m，则主、从机器人基坐标系间的旋转矩阵和平移矩阵为：

进而由公式（5）计算得到从机器人的工作空间解集为：

式中：si、ci-sinqi和cosqi，sij、cij-sin（qi+qj）和cos（qi+qj），且qimin£qi£qi-max，i=1，2，3。

根据上述主、从机器人工作空间解集Wm和Wsw，按照1.2中方法，可以分别得到两台机器人工作空间的点云数据。一般情况下，随机点数量越多，机器人工作空间计算精度越高，但当随机点数多达一定数量时，工作空间点云图像已经非常清晰，增大随机点数量的意义不大。这里多次试验后最终确定主、从机器人各取随机点15万为佳，并将结果绘制在同一坐标系下，得到图5所示的点云图，其中蓝色、红色区域分别表示主、从机器人工作空间的点云图。

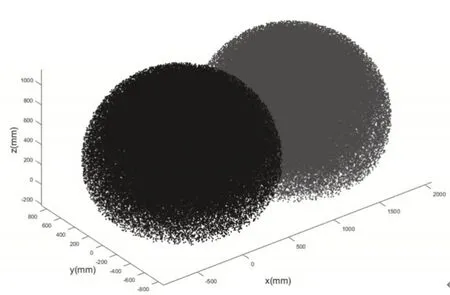
图5 主、从机器人工作空间点云Fig.5 Point Cloud of Master and Slave Robot Workspace

利用1.3中给出的协作工作空间点云获取方法，提取上图的协作区域点云，共寻到69370个点，结果如图6所示。基于a-Shape算法对协作工作空间进行三维重建，为确定出合适的a值，这里在区间（0，150）内随机选取了1000组数据，并计算出对应的多面体体积Vi，将结果以坐标（ai，Vi）的形式记录，结果如图7所示。

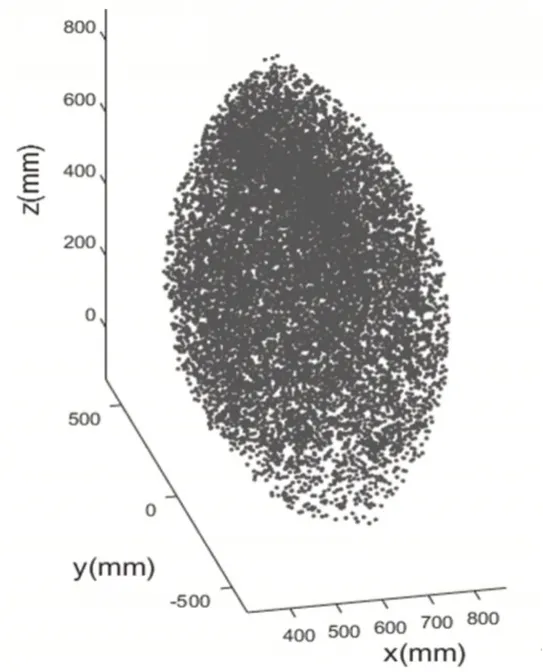
图6 协作工作空间点云Fig.6 Collaborative Workspace Point Cloud

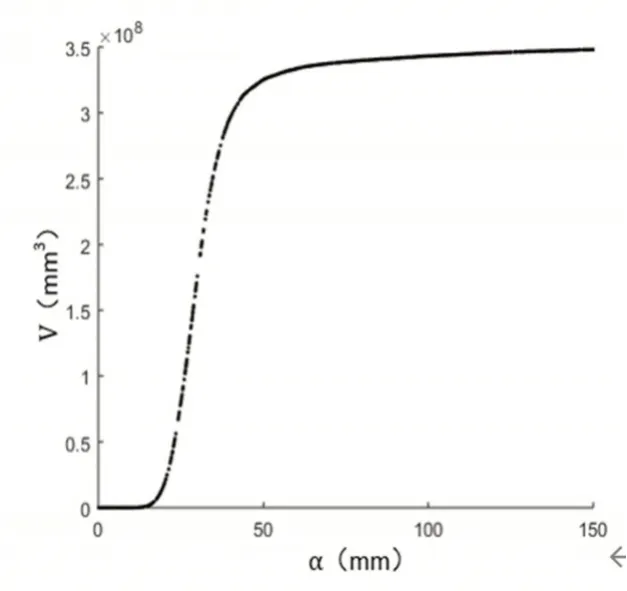
图7 体积与参数a关系Fig.7 The Relationship between Volume and Parameter a

可以明显的看到，体积随着参数a的变化曲线有着较强的连续性和规律性，在a值较小的一段区间内，体积一直为零，这是由于a值过小导致重建的曲面空洞太多，表现为一些离散的三角片，如图8（a）所示为a=15mm对应的重构结果；当a超过图中第一个“转折点”后，体积值发生明显变化，随着参数的增加上升趋势加快，这一过程重建效果逐步完善；当a超过第二个“转折点”后，曲线明显变得平缓，体积值基本无变化，表明重建效果已达最佳，再增加a值已经没有意义，只会保留更多的三角片面。因此，选取本例中第二个转折点对应的a值为合适的参数，此时a=49.6572mm，计算体积V=0.32493m3，对应的重建结果如图8（b）所示。为了验证该方法的重建精度，将协作区域点云与图8中a=49.6572mm的重建曲面一同绘制，进行对比分析，如图8（c）所示，可以看到蓝色的点云轮廓边界点均匀分布在曲面上，表明该方法具有较高的精度。

图8 协作工作空间重建效果Fig.8 Reconstruction Results of Collaborative Workspace

由于主、从机器人型号相同，只对主机器人的工作空间点云进行三维重建，其体积与参数a的关系如图9（a）所示，确定参数a=44.2570mm，对应体积为2.22039m3，采用该参数的重建结果如图9（b）所示。为了便于分析，将主、从机器人工作空间和协作工作空间的重建结果相关数据进行整理，如表2所示。

表2 重建结果相关数据Tab.2 Ralated Data of the Reconstruction Results

图9 主机器人工作空间三维重建Fig.9 3D Reconstruction of the Master Robot Workspace

为了验证volume（）函数对重建多面体体积计算的可靠性，这里以球形工作空间的重建结果体积计算为例，对计算精度进行验证。随机点数取3万，计算结果如表3所示。可以看到，几种不同半径的球体采用α-Shape三维重建后，应用volume（）函数计算的体积值误差均小于1%，说明该方法比较可靠。

表3 体积计算精度Tab.3 Volumetric Accuracy

工业中，机器人协作完成搬运任务一般对协作工作空间的要求不高，但完成装配、焊接、涂胶等任务或研究避碰问题时，协作工作空间的相关数据就有着重要的参考意义。例如，采用这里方法可以在协同作业的多台机器人安装固定之前，计算得到工作空间与协作工作空间的相关数据，进而结合实际的任务需求判断机器人布局方式是否满足要求，避免多次安装所带来的额外人力及物力，提高生产效率。本例中，根据工作空间在空间的分布状况以及协作区域相对整个机器人工作空间的占比，双机器人相对布局比较利于机器人协作完成一定的装配任务。

若只将公式（11）中两台机器人基坐标系间平移矩阵第一个元素分别设置为600mm和1600mm，不改变两台机器人的姿态和其他条件，采用相同的方法计算得到协作工作空间体积分别为1.12236m3和0.05296m3，协作空间体积占比分别为50.55%和2.39%。容易看出，0.6m的布局下协作区域过大，机器人与工具、工件以及机器人与机器人之间容易发生碰撞；1.6m的布局下，协作工作空间体积过小，主、从机器人在该区域作业时关节易出现奇异值而且TCP点不能以多种姿态到达某个点，两种布局均不满足要求。

5 结论

通过机器人运动学方程结合蒙特卡罗法得到了主、从机器人工作空间的点云模型；分析了求交集法提取协作空间点的缺点，并给出了通过计算点与点距离并加入一定阈值的判断方法，有效的提取到了协作区域的点云；为了使工作空间可视化和数字化，提高应用性，这里运用三维重建相关理论，采用a-Shape算法分别对机器人工作空间和协作工作空间进行了重建，以形体的体积计算值作为参考衡量重构效果，给出了基于体积值的参数a确定方法，并得到了较好的重建效果；最后对重建结果的相关数据进行分析，表明该方法对规划机器人的布局方式具有较强的参考意义，为工业中机器人协作完成各种任务提供一定的理论依据。