结合前馈与反馈控制机器人伺服系统研究

2021-10-20崔国华张智涛刘宏业

机械设计与制造 2021年10期

崔国华，冀霖，张智涛，刘宏业

（1.河北工程大学机械与装备工程学院，河北邯郸056038；2.天津扬天科技有限公司，天津300073）

1 引言

随着新一代高性能机电一体化产品工业机器人的产生，其高精度的伺服控制系统作为机器人的核心技术，受到学者广泛研究。传统的伺服控制方法由于系统自身的强耦合、非线性时变等特征，难以建立精确的数学模型，不能满足工业机器人高速、高精度的动态跟踪特性［1-2］。文献采用模糊PID控制算法，通过人工智能把经验值建立为控制模型，实现参数最优化［3］。文献采用一种基于小波神经网络的自适应反推控制策略，通过自适应调节反推控制器的输出，继而达到良好的位置跟踪效果［4］。上面两种方法虽让能改善伺服系统的动态特性，但求解复杂，实时计算处理难度大，实现困难。文献采用惯量前馈控制，通过自适应辨识电机的转动惯量，确定加速度前馈系数［5］。该方法能有效提高伺服系统的响应速度和控制精度，但容易发生超调现象。

这里采用在前馈控制的基础上引入微分负反馈控制的复合控制的方法，在提高伺服系统控制精度和动态跟踪特性的情况下，避免对非连续信号产生的超调现象。在MATLAB/Simulink中建立模型进行仿真分析，并设计实验对机器人进行轨迹规划，通过FARO标定仪测定在不同伺服控制模式下机器人运行轨迹时的定位精度与超调量，以此来验证该方法的有效性。

2 微分反馈与前馈复合控制系统设计

为了使系统既具有快速响应，又不产生过高的超调量，在传统的位置反馈回路中加入微分反馈，其位置环微分反馈控制图，如图1所示。

图1 位置环微分反馈系统控制图Fig.1 Position Loop Differential Feedback System Control Chart

可由图1可得出该位置环微分反馈系统的传递函数为：

带入式（1）中可得：

式中：Kp-位置环比例系数；Kv-速度环PI比例系数；Kc-电流环等效惯性环节；τv-速度环时间常数；ξi-阻尼系数；τα-微分负反馈系数，其中ξi决定了系统的振动情况及系统的超调量大小。

由式（3）可知，阻尼系数ξi与微分反馈时间常数τα成正比，由于Kp值较大，少量的反馈补偿就可能会导致系统过阻尼，过阻尼会大大降低系统的响应速度，欠阻尼则会使系统发生超调，因此，一般取系统的临界阻尼附近ξi=［0.8，0.9］之间，这里取ξi为0.8，从而保证系统响应又快、又无超调。

采用微分反馈与前馈相结合的控制策略，得其控制系统，如图2所示；将机器人单关节等效为二阶阻尼系统，可得其传递函数：

图2 微分反馈和速度电流前馈系统控制框图Fig.2 Control Block Diagram of Differential Feedback and Speed Current Feedforward System

根据式（5）令H（s）=1，得到速度前馈函数加速度前馈函数由此可知，当引入微分反馈后，电流环前馈函数保持不变，速度环前馈函数为一阶微分函数，因此，得到修正后的前馈函数分别为：

3 实验设计分析

为了证明采用结合前馈与微分反馈控制的方法能够使机器人既能保持良好的动态跟踪性能又不发生超调，这里针对机器人末端轨迹进行路径规划并对机器人性能测量的三个重要指标即绝对定位精度（AT）、重复定位精度（RT）、超调量（OV）进行实验分析。

3.1 机器人轨迹规划

工业机器人在运动过程中，伺服电机要严格满足位置、角速度、角加速度的边界条件。为此，一般采用五次多项式来进行轨迹规划：

当初始速度ω0=0和终止速度ω1=0时，角加速度约束条件为：

关节机器人的运动需要多电机联合同步控制，且在运动过程中动态惯量、粘性摩擦等参数变化比较大，所以使得每个关节在运行时，都必须达到高精度、高鲁棒性、快速响应和无超调的要求。

本次实验选用5kg协作机器人进行路径规划，根据机器人的D-H参数，通过雅克比矩阵可得出机器人末端可达的工作区间，并通过多次实验测试，选取出内部的一个立方体进行轨迹规划，其选取原则为：（1）该立方体位于工作区间中应用较多；（2）该立方体应具有最大的体积，并且棱边平行于基坐标系。为了增加实验的准确性，在该立方体内设计四条轨迹，如图3所示。

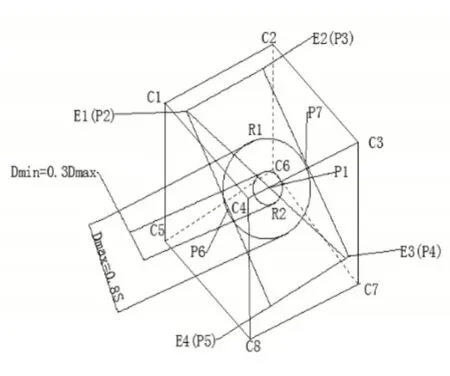
图3 实验数据所测得立方体Fig.3 Test Data Measured by The Experimental Data

进行实验分析：

（1）矩形轨迹：E1→E2→E3→E4

（2）直线轨迹：P2→P4

（3）大圆轨迹：R1

（4）小圆轨迹：R2

其中，C1→C8-所取立方体；S-立方体的边长；取大圆直径Dmax=0.8S，小圆直径Dmin=0.3Dmax

3.2 性能测量指标

3.2.1 绝对定位精度（AT）

轨迹精度表示机器人在同一方向上沿指令轨迹n次移动的能力，其位置轨迹精度（ATP）为：

式中：xcj、ycj、zcj-轨迹第i点的坐标；

xij、yij、zij-第j条实到轨迹与第i个正交平面焦点的坐标；

式中：aci、bci、cci-（xci、yci、zci）处的指令姿态；aij、bij、cij-（xij、yij、zij）处的指令姿态。

3.2.2 重复定位精度（RT）

轨迹重复性表示机器人对同一指令轨迹重复n次时实到轨迹的一致程度，其中：

式中：li-实到位姿与各个实到位姿集群重心间的距离；Sli-n次li与其均值-li之间的标准差。

3.2.3 超调量（OV）

位置超调量是衡量机器人平稳、准确的停在实到位姿的能力，其与位置稳定时间有关，即机器人第一次进入门限带在超出门限带后瞬时位置与实到稳定位置的最大距离，如图4所示；可得：

图4 稳定时间和位置超调量Fig.4 Stabilization Time and Position Overshoot

式中：i-机器人进入门限带后测量的采样点信号。

4 仿真分析与实验验证

4.1 仿真分析

将前馈与微分反馈控制系统在MATLAB/Simulink环境下建立的仿真模型，如图5所示。

图5 位置控制系统模型Fig.5 Position Control System Model

其中主要参数如下：

图6 位置伺服系统仿真Fig.6 Simulation of Position Servo System

对于阶跃位置响应来说，前馈控制相比于传统伺服控制而言，波动偏差减小，变化速度减慢，在0.7s处使系统趋于稳定，但都存在较大的超调量，严重影响伺服系统的性能。在前馈控制的基础上加上微分负反馈后，使变化速度开始减慢，在无超调的情况下能够达到快速响应，并最终趋于稳定，显著提高了机器人伺服系统的性能。

4.2 实验验证

实验所用的5kg协作机器人和FARO标定仪，如图7所示。

图7 实验所用机器人与标定仪Fig.7 Robot and Calibrator Used in Experiment

本次实验分为3组，第一组为普通PID下的伺服参数性能测试，第二组为引入前馈控制的伺服参数性能测试，第三组为前馈与反馈复合控制下的伺服参数性能测试，该3组实验均在同一套PID参数下分别运行以上规划的4种轨迹进行对比测试。

将测试条件设定为机器人在世界坐标系下20%负载运行，TCP速度为0.3m/s，门限带设为0.1mm，每条轨迹重复10次测试，其中矩形、直线、大圆、小圆轨迹分别由21400、18185、31755、14781个理论位姿点生成，通过MATLAB计算出每一个采样点与理论位姿点的偏差，根据式（8）、（10）、（12）可得出机器人的绝对定位精度、重复定位精度、超调量及稳定时间，如表1～3所示。

表1 普通PID下的性能测试Tab.1 Performance Testing under Normal PID

表2 前馈控制下的性能测试Tab.2 Performance Testing under Feed-forword Control

在上述实验过程中，普通PID调节下的机器人具有明显抖动，由表1可知，机器人的绝对定位误差大、超调量大、稳定时间较短；加入前馈控制的机器人运行平稳，且能够大幅提高其定位精度和跟踪特性，但仍有明显的超调；通过对比表3实验数据可知，采用前馈与微分反馈复合控制的机器人不仅能够平稳运行，保持良好的动态跟踪特性和定位精度，而且在抑制超调量上有明显改善，显著提高了机器人伺服系统的性能。