精英协作引导花授粉算法及机器人导航路径规划

朱旭东

（无锡工艺职业技术学院，江苏 宜兴214200）

1 引言

花授粉算法模拟自然界中自花授粉和异花授粉而提出，具有参数少、原理简单、寻优性能佳等诸多优点［1］。与其它启发式算法一致，花授粉算法也存在探索（全局搜索）与开采（局部搜索）之间的矛盾与平衡问题，使算法的收敛与寻优能力存在矛盾。因此，对算法进行改进而寻找探索与开采之间的平衡，对提高算法的寻优性能具有明显作用。

花授粉算法寻优性能的缺陷主要体现在两个方面：一是算法运行过程中过慢的收敛速度；二是随着算法迭代，较差的进化能力使算法过早停滞在局部最优。改进思路也从两个方面入手：一是将花授粉算法与其他算法融合，实现优势互补；二是改进算法的局部搜索和全局搜索过程，寻找两者更加的平衡点。文献［2］将和声搜索算法融入到花授粉算法中，提高了算法的收敛速度，同时使用折射原理提高了算法的搜索精度；文献［3］将模拟退火算法降温操作融入到花授粉算法中，增加了种群多样性，同时提高了算法的整体寻优性能；文献［4］使用逻辑自映射函数对花粉进行混沌扰动，改善了花授粉算法缺乏变异机制的问题，解决了算法后期趋同问题；文献［5］针对全局搜索过程引入全局平均最优花粉位置和动态权重递减因子，牵引花粉朝正确方向搜索，同时使用Cauchy变异增加种群多样性，提升了算法的寻优精度和速度。针对不同的问题，启发式算法具有不同的改进方法和优化方式。另外，群智能算法的两个平衡点研究难以解决，分别是收敛性与寻优精度的平衡研究、全局搜索与局部搜索的平衡研究。

这里研究了花授粉算法的改进问题，通过在花授粉算法中添加对立点初始化策略、精英协作引导策略和动态转换概率策略等，达到提高算法寻优精度和稳定性的目的。并将此算法应用于机器人路径规划，达到了提高路径质量和规划稳定性的目的。

2 花授粉算法

2.1 花授粉算法的仿生学原理分析

花授粉算法是模拟自然界中的自花授粉和异花授粉现象而提出的。自花授粉的传播距离较近，是一种局部搜索方式。异花授粉依赖蜜蜂、蝴蝶等昆虫以Levy飞行的方式传播，花粉的传播距离较远，是一种全局搜索方式［6］。

在算法中为了实现全局搜索和局部搜索的切换，设置了一个转换概率p。转换概率的设置至关重要，用于平衡与协调局部搜索和全局搜索。花粉位置改变前后的优劣程度使用适应度函数表征，并使用适者生存原则进行选择。总的来讲，花粉传播现象与花授粉算法的对应关系如下：（1）通过对花粉进行合理编码，将花粉位置与待搜索空间的点一一对应；（2）自花授粉对应局部搜索过程，异花授粉对应全局搜索过程；（3）花粉所处位置的优劣与待优化问题的适应度函数值一一对应；（4）花粉传播前后的选择使用适者生存原则进行选择。

2.2 花授粉算法简介

花授粉算法核心思想为：设置一个转换概率p和随机数rand∈(0,1)，当rand＜p则进行全局搜索，若rand≥p则进行局部搜索。算法实现主要包括初始化、全局搜索与局部搜索机制、花粉选择等关键步骤。

（1）花粉位置初始化。花粉位置使用随机方式进行初始化，为：

式中：Xi-花粉第i维位置；ri-［0，1］间随机数花粉第i维位置的最小值和最大值。

（2）全局搜索。全局搜索模拟Levy飞行方式进行位置更新［7］，方法为：

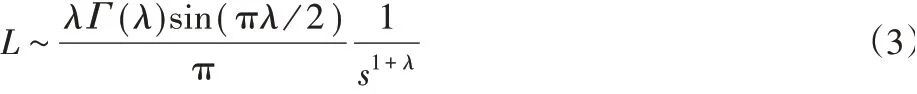
式中：λ=1.5，Γ(λ)-标准gamma函数；s-利用Mantegna算法产生的步长，即：

式中：v～N(0,1)，μ～N(0,σ2)，方差σ2的计算方法为：

（3）局部搜索。局部搜索以异于自身的两个花粉差分为牵引［8］，即

（4）适者生存。花粉每更新一步，则判断更新前后位置优劣，并根据适者生存原则进行选择［9］。记f()为目标函数，目标函数越小则花粉位置越优。当时进行位置更新，否则不进行位置更新。花粉位置更新后进行全局最优判断，若则更新全局最优，否则不更新。

（5）算法结束条件。当所有花粉完成一次迭代时才进入下一轮迭代，当迭代次数达到最大迭代次数Tmax时算法停止，输出全局最优即为花粉最优位置。

3 精英协作引导花授粉算法

3.1 算法缺陷分析

对花授粉算法原理及实现方式进行深入分析，可以看出算法的如下缺陷：（1）使用完全随机的方式进行位置初始化，花粉可能在某区域较为集中，而不够分散；（2）随着算法的迭代，在全局最优g*的牵引作用下，花粉聚集在全局最优附近，使得g*-Xt i较小或约为0，此时式（2）给出的全局搜索方式几乎没有进化能力，使算法停滞在某一局部最优处；（3）转换概率用于平衡与调节全局搜索和局部搜索，但是固定的转换概率难以较好适应算法全过程。本节针对以上分析出的几点缺陷提出改进方法，分别提出了对立点初始化方法、精英协作引导方法、动态自适应转换概率等。

3.2 改进策略

（1）对立点初始化方法。

以花粉第i维为例，对立点定义方式，如图1所示。

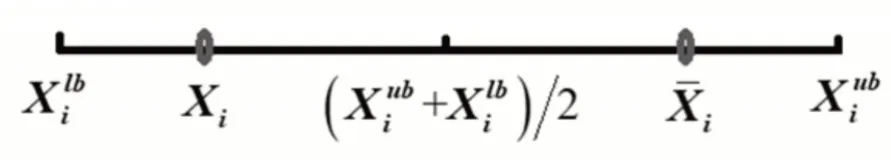
图1 对称点示意图Fig.1 Opposing Point Sketch

经分析可知，取值范围内的任意一点其对称点是唯一存在的，计算方法为：

对立点初始化方法为：对于种群规模为N的初始化问题，首先使用随机方式进行生成N个初始位置，而后计算每个花粉对立点，将原始位置与对立点位置共2N个进行适应度排序，选择前N个个体作为种群初始位置。

（2）精英协作引导方法。

随着算法的迭代，花粉聚集在全局最优g*附近，使得g*-按照全局搜索方式有，这意味着算法几乎失去了进化能力，极易陷入当前最优。深入进行机理分析可知，单独的种群最优进行引导过于单调，没有充分发挥种群智慧。为了解决这一问题，这里选择种群中适应度前三的花粉（即精英花粉），精英花粉进行协作组成新的花粉位置对全局搜索进行引导。精英协作如图2所示。

图2 精英协作方式Fig.2 Elite Collaboration Manner

为了体现不同精英花粉在协作与协商过程中的话语权，依据花粉的目标函数值为其赋不同的权值。以目标函数f()越小越优为例，精英花粉权值赋值方法为：

式中：wgb1、wgb2、wgb3-不同精英的权值。则精英的协作位置为：

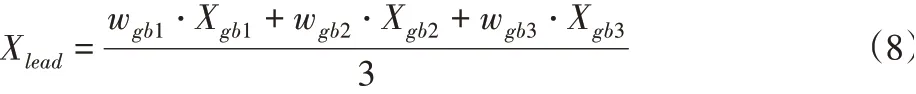
式中：Xlead-精英花粉协作位置，使用Xlead代替式（2）中的全局最优就实现了精英协作策略对全局搜索的引导。

（3）动态自适应转换概率。

前文中讲到，转换概率用于平衡全局搜索与局部搜索，对算法的寻优性能至关重要。算法初期，算法应更大概率进行全局搜索，在全局范围内找到最优解邻域；算法后期，算法应更加倾向于进行局部搜索，在小范围内提高寻优精度，同时促进算法收敛。基于这一思考，这里使用动态自适应转换概率代替固定转换概率。方法为：

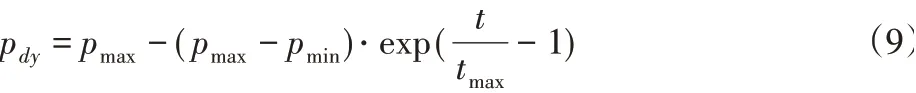
式中：pdy-动态转换概率；pmax、pmin-最大最小转换概率；tmax-最大迭代次数；t-当前迭代次数。

3.3 精英协作引导花授粉算法流程

以传统花授粉算法流程为基础，将对立点初始化方法、精英协作引导策略、动态转换概率融入其中，得到精英协作引导花授粉算法流程如下：

Step1：初始化算法参数，包括种群规模N，算法最大迭代次数tmax，最大最小转换概率pmax、pmin；

Step2：使用对立点初始化方法生成并选择初始种群；

Step3：对转化概率进行动态更新，当rand＜pdy时执行精英协作的全局搜索策略，当rand≥pdy时执行局部搜索策略；

Step4：计算花粉位置更新前后的目标函数值，依据适者生存的原则选择目标函数值小的花粉进入下一轮迭代；

Step5：判断是否达到最大迭代次数，若否则转至Step3；若是则输出全局最优位置，算法结束。

4 改进花授粉算法性能测试

4.1 测试环境及测试函数

使用Matlab（R2010b）软件对算法性能进行测试，使用的测试函数从非固定维数单模态标准函数和非固定维数多模态标准函数中随机选取，如表1所示。

表1 测试函数Tab.1 Testing Function

4.2 测试结果分析

为了验证三种改进措施之间的关联性和耦合性，记传统花授粉算法为FPA，融入对立点初始化的花授粉算法记为IFPA1，融入精英协作引导策略的花授粉算法记为IFPA2，融入动态自适应转换概率的花授粉算法记为IPFA3，融入全部改进策略的花授粉算法记为IPFA。

为了保证公平公正，算法共有的参数设置为相同值，种群规模N=30，最大迭代次数tamx=500，固定转换概率p=0.8，转换概率最大值最小值分别为pmax=0.9、pmin=0.7。测试函数维度统一设置为50。为了防止偶然性因素影响，每种算法各自独立运行10次，统计每次最优结果的平均值和标准差，如表2所示。

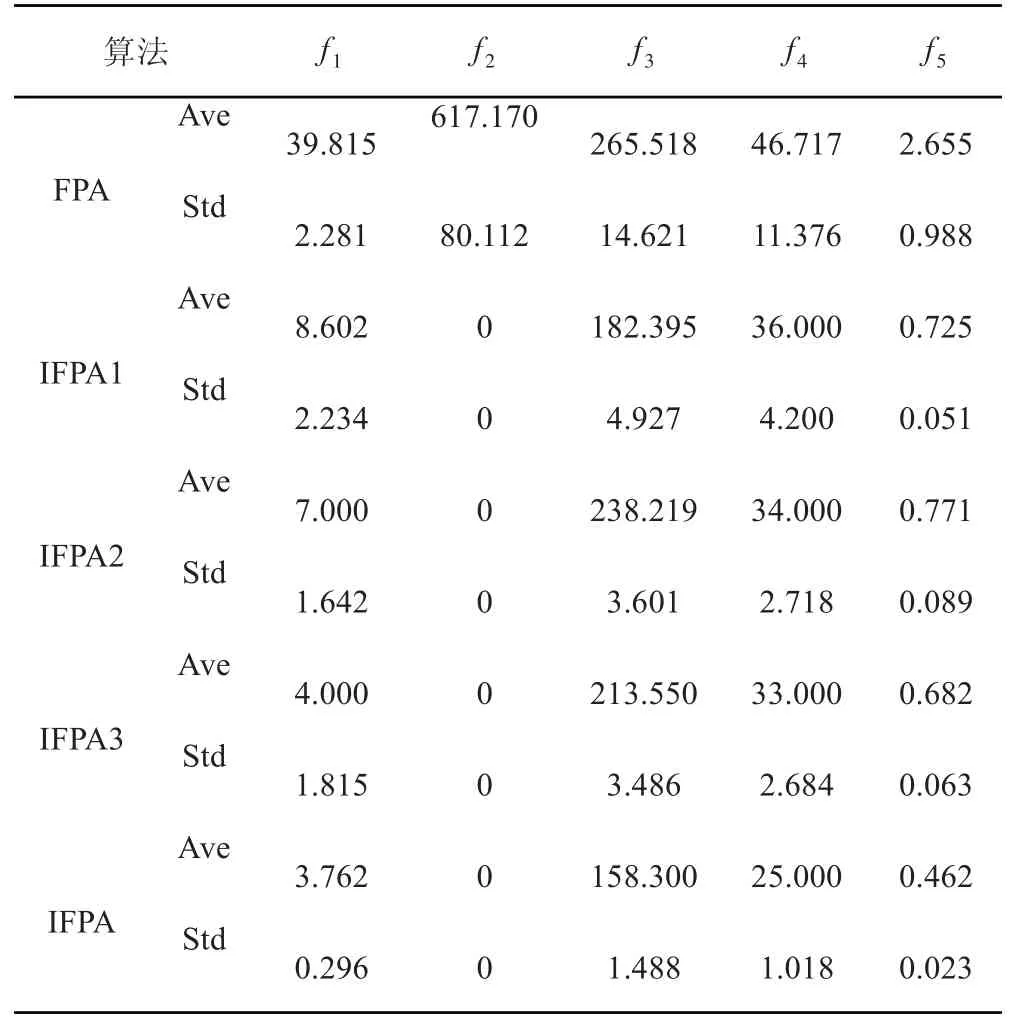
表2 测试结果Tab.2 Testing Result

分析表2中的测试数据可以得出以下结论：（1）融合任意一个改进措施的花授粉算法寻优精度和寻优稳定性都优于传统算法，说明三项改进措施都是有效且必要的；（2）融合三项改进措施的精英协作花授粉算法具有最佳的寻优精度和寻优稳定性，说明三向改进措施之间没有发生有害性耦合与关联。综上所述，精英协作引导花授粉算法具有最佳的寻优精度和寻优稳定性。

5 机器人路径规划应用

5.1 机器人路径规划建模

机器人路径规划思路如图3所示，在原坐标系XOY中确定出机器人起始点和目标点，而后将起点至终点使用直线连接，连接线与X轴夹角记为θ。以起点至终点接线为X’轴建立新坐标系X’SY’，在起点S与终点T之间使用D-1条平行线将线段ST等分为D段。那么，只要规划出每条平行线Li的纵坐标值，将其进行平滑连接就得到了机器人路径。经过以上分析过程，这里将路径规划问题转化为平行线上Li的纵坐标规划问题。

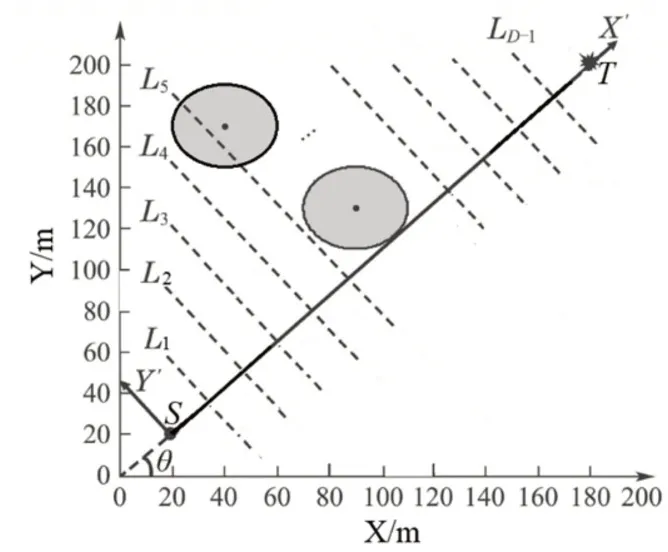
图3 路径规划思路Fig.3 Path Planning Thought

这里的路径规划目标为：在避障的前提下规划出全局最短路径［10］，根据这一规划目标，目标函数构造为：

式中：Leng-路径长度；P-机器人碰撞标志变量；β-足够大的系数，用于排除发生碰撞的路径，在此取β=100。路径长度Leng为：

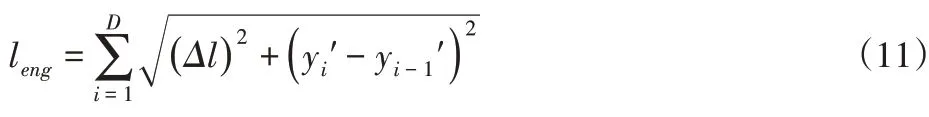
为了方便进行碰撞判断，将所有障碍物膨胀为圆形，碰撞标志变量P计算方法为：

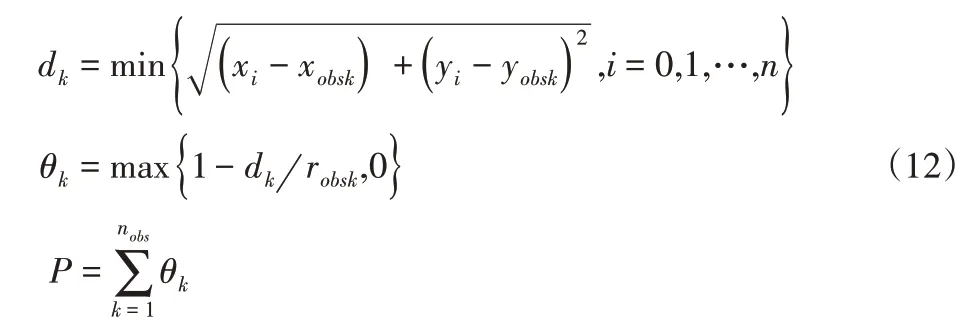
式中：(xobsk,yobsk)-第k个障碍物圆心；(xi,yi)-插值点坐标；dk-插值点与第k个障碍物的距离最小值；robsk-第k个障碍物的半径；θk-轨迹与第k个障碍物的碰撞标志值；nobs-所有障碍物数量。

分析式（12）可知，当存在某一插入点与障碍物中心距离小于障碍物半径时，此时机器人与障碍物发生碰撞，同时θk＞0，则P＞0，结合式（10）在系数β的放大作用下，有z=L(1+βP)≫L，此时z值较大，不会成为最优路径。当所有插入点与障碍物不发生碰撞时，θk=0，P=0，1+βP=1，此时z=L，长度最短的无碰路径即为最优路径。

根据以上机器人路径规划模型，花粉位置使用十进制编码方式，花粉维度设置为D-1维，编码方法为

5.2 机器人路径规划性能验证

如图4所示环境为机器人工作环境，图中蓝色圆圈为障碍物区域。同时使用传统花授粉算法与精英协商引导花授粉算法进行路径规划，算法的参数设置与4.2节一致，每种算法各自独立规划10次，统计10次最优路径长度，结果如图5、表3所示。

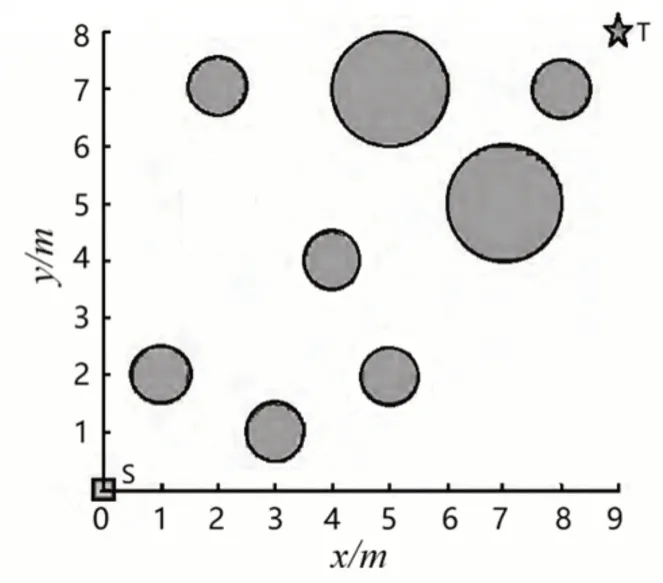
图4 机器人工作环境Fig.4 Robot Working Environment

表3 路径规划统计值Tab.3 Path Planning Statistics

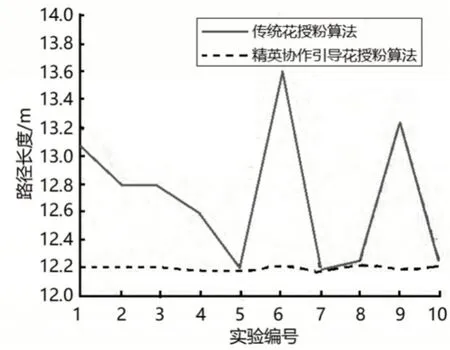
图5 路径规划结果Fig.5 Path Planning Result

由图5和表3可以明显看出，精英协作引导花授粉算法规划路径均值比传统算法减少了4.01%，标准差减少了一个数量级以上。说明精英协作引导花授粉算法的路径规划稳定性远远优于传统花授粉算法，规划的路径质量也优于传统算法。这意味着，精英协作引导花授粉算法不仅寻优精度极佳，而且稳定性很好，每次都能够搜索到极佳路径。这是因为对立点初始化方法提高了初始种群质量，精英协作引导全局搜索的方式提高了算法搜索效率和质量，动态转换概率策略有效平衡了全局搜索与局部搜索，使算法寻优精度和稳定性明显优于传统算法。精英协作引导花授粉算法与传统算法规划的最优路径，如图6所示。

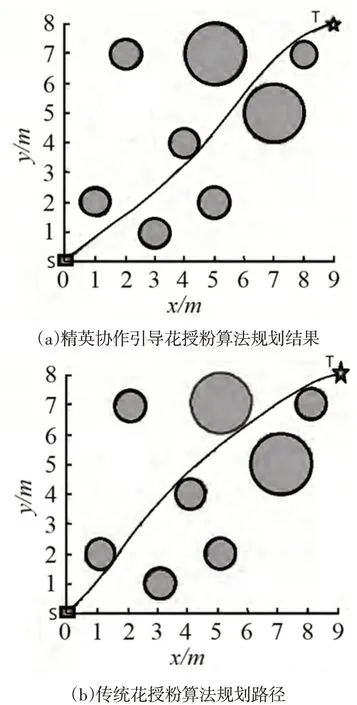
图6 两种算法的规划结果Fig.6 Path Planning Result by the Two Algorithms

从图6中可以看出，两种算法规划的路径均安全且平滑，能够满足机器人行驶的动力学要求。结合图5与表3，精英协作引导花授粉算法在机器人路径规划中寻优精度高且稳定性极好。

6 结论

这里研究了花授粉算法的改进问题，给出了对立点初始化、精英协作引导全局搜索、动态转换概率等改进策略，从而提出了精英协作引导花授粉算法，经测试得出了以下结论：（1）每种改进策略都能够提高算法性能，且彼此间不存在抵消性耦合；（2）精英协作引导花授粉算法在机器人路径规划中寻优精度高、稳定性能好。