车辆前端吸能部件多目标耐撞性遗传优化

胡 贇，李文凤，宋敏杰

（1.南昌大学机电工程学院，江西 南昌330031；2.江铃汽车有限公司，江西 南昌330031）

1 引言

耐撞性是衡量车辆在遭受严重撞击后保护乘客避免死亡或受伤的重要安全性指标。为节约车辆耐撞性试验所耗费的时间与财力成本，通常采用计算机仿真参数优化设计来替代真实的车辆耐撞性物理试验。事实上，车辆耐撞性优化一般需要多次仿真试验来完成，而全尺寸的车辆耐撞性仿真又需要耗费大量的计算资源。为克服这一问题，目前的做法主要是采用响应面法、Kriging以及径向基函数来完成［1-6］。但是很多文献指出，采样点与代理模型的选择能在很大程度上影响车辆耐撞性代理模型的响应精度。采样点的选择如果在整个设计空间分布不均匀、代理模型的柔韧性不足，往往就会导致低精度的响应结果。

为此，文献［7］提出了一种序列响应面法，通过移动、缩放等方式不断地在设计空间内更新兴趣域。采用最小距离选择法获得最优解。文献［8］提出一种前向步进回归技术来拟合仿真模型输入输出之间的关系，通过对100%正面碰撞和40%正面偏置碰撞的耐撞性问题研究，表明了该方法的有效性。需要注意的是，由于耐撞性问题的强非线性性质，为避免最优解陷入局部最优，优化方法应当具备全局寻优的能力。无论采用什么样的抽样技术或代理模型，前提都必须保证仿真模型是可信的，最好是经由试验验证［9-11］。

这里通过将仿真模型与真实试验结果对标，确保仿真模型精度，采用具有高效抽样效率的均匀设计法完成样本点的采集，通过一个三层神经网络模型来克服耐撞性问题的强非线性。基于多目标遗传优化算法NSGA-Ⅱ来完成最优解寻优。

2 车辆耐撞性仿真模型建立

车辆耐撞性仿真模型涉及到不同尺度的零部件，包含金属、非金属材料，从而导致车辆耐撞性仿真试验是一个高度非线性与耗时的过程。为提高计算效率并将仿真精度保证在一个可接受的范围内，诸如关键部件网格的纵横比、四边形网格的翘曲程度以及三边形与四边形网格的内角均需要检查。为简化模型，不计车辆内饰与管线的影响。最终建立的全尺寸车辆模型包含1523000个单元与1533000个节点。如图1所示，是车辆撞击过程中各部分能量变化曲线图，从图中可以看到动能和内能大约是在8ms处开始交换，沙漏能大约是845J，界面滑移能大约是804J，分别占到总能量的0.49%和0.46%，总能量保持不变，表明所建立的仿真模型在整个碰撞过程中遵循能量守恒。

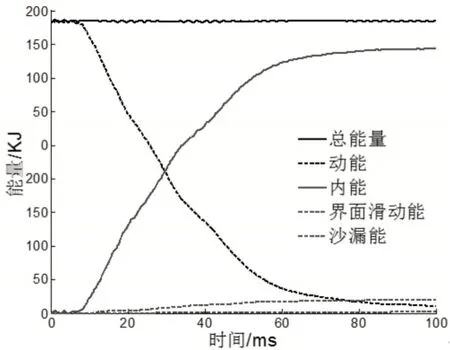
图1 能量变化曲线Fig.1 Energy Change Curve

如图2所示，是车辆撞击过程中的质量变化曲线，从图中可以看到质量最大增加6.10kg，只占总质量的0.34%。无论是车辆撞击过程中的能量变化还是质量变化，变化量均在模型可信度推荐值5%之内。

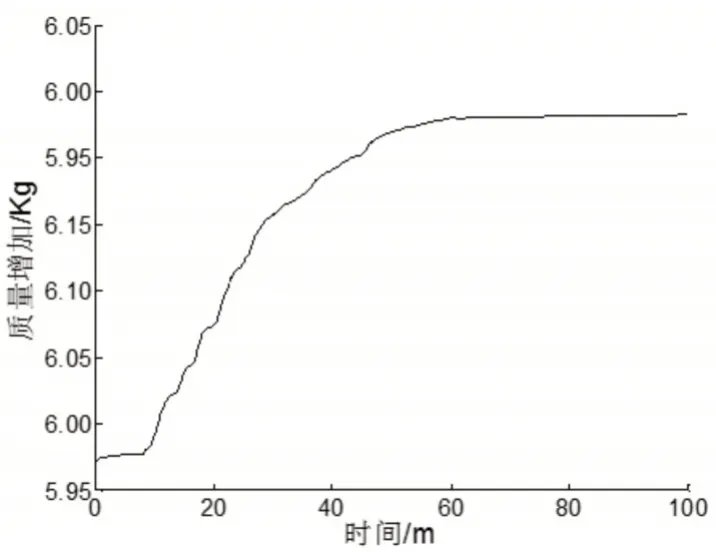
图2 质量增加曲线Fig.2 Mass Change Curve

3 车辆耐撞性仿真模型验证

尽管车辆耐撞性仿真模型的精确性已经经过总能量变化以及质量变化检查，但模型在应用到耐撞性参数优化之前，仍然需要经过试验验证。考虑车辆耐撞性研究是以保护乘员安全性为主要目的，这里加速度历史变化曲线与位移历史变化曲线在车头靠近驾驶员座椅左侧立柱B点测量，如图3所示。

图3 立柱B点位置示意图Fig.3 Position of B Point on the Left Pillar

这里以这两个参数作为仿真模型可信度度量依据，对比结果如图4所示。从图中可以看到，仿真曲线与试验曲线之间的变化趋势吻合良好。

图4 试验与仿真曲线对比Fig.4 Comparison of The Curves Between Simulation and Experimental

如图5所示，是车辆前端耐撞性仿真结果与试验结果之间的对比图。图中明显的显示两者之间车辆前端的变形是比较一致的。因此，这里建立的车辆耐撞性仿真模型具有很高的仿真精度，能够被用来研究车辆耐撞性优化设计。

图5 车辆前端压溃对比图Fig.5 Comparison of Final Deformation Between Simulation and Experimental

4 代理模型

4.1 样本点设计

代理模型替代仿真模型可以节约大量的模拟时间。考虑人工神经网络在处理非线性问题时，具有非常好的柔韧性，这里采用人工神经网络来完成车辆耐撞性代理模型建立。为获取一个有效的人工神经网络，样本点的选择必须在整个设计空间内具有代表性。这里提出采用均匀设计法来完成样本点的设计。与随机法、中心复合法以及矩法等试验设计方法相比，均匀设计法最大的优点是不受设计变量增加的影响，它只需少数几个样本点就能保证结果的一致性。如此一来，可以节约大量的仿真模拟时间，提高设计效率［12-13］。

车辆前端部件是车辆发生全正面碰撞时的主要吸能部件。如图6所示，分别选择了吸能盒上板厚度、吸能盒下板厚度、前纵梁加强板厚度以及前纵梁U型板厚度等四个车辆主要吸能部件作为车辆耐撞性优化设计对象。边界条件定义如表1所示。

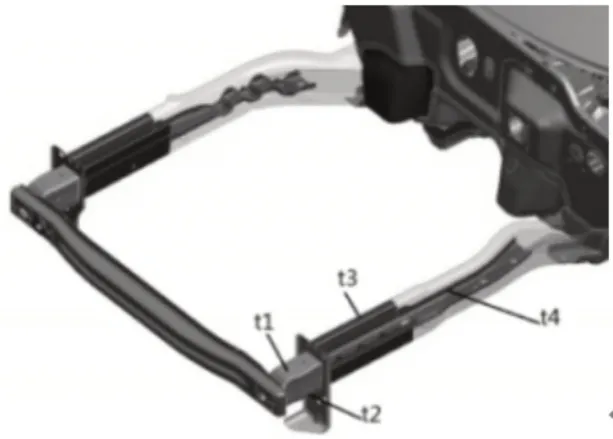
图6 优化对象Fig.6 Optimal Objectives

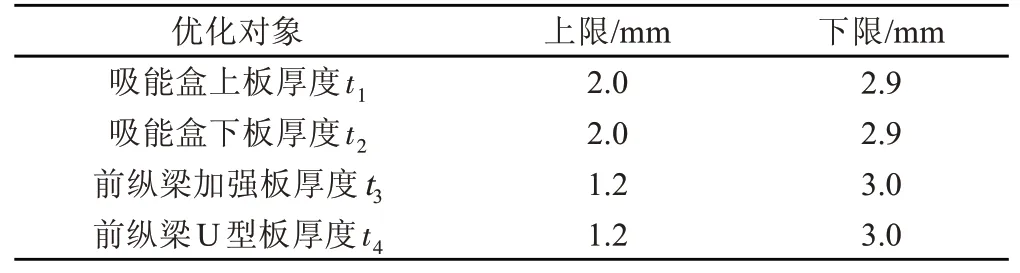
表1 优化参数的边界条件Tab.1 Boundary conditions of optimization parameters

为方便地选取均匀设计表，将设计空间均匀地分成10个水平，每一个水平分别编号，如1、2、3等。考虑因素水平，选择U10(108)最为均匀设计方案，其中U表示均匀设计表，10表示设计变量水平，8表示均匀设计表最大列数。由于只包含四个设计变量，根据方开泰14的推荐，选择U10(108)中的1、3、4、5列作为试验安排依据。新的均匀设计表U10(104)如表2所示，其最小分散性只有0.2236。根据均匀设计表得出的试验方案，仿真次数只需10次即可获得在设计空间均匀分布的样本点，而中心复合法、矩法以及正交试验法分别需要25次、25次以及100次。这充分体现了均匀设计在样本点选择时的高效性。用来表征车辆前度部件吸能能力的参数主要有最大加速度A(t)、立柱B点最大位移D(t)以及吸能比E(t)（以单位重量内吸收的能量）。这部分根据试验和仿真得到的数据列于表2最右侧。

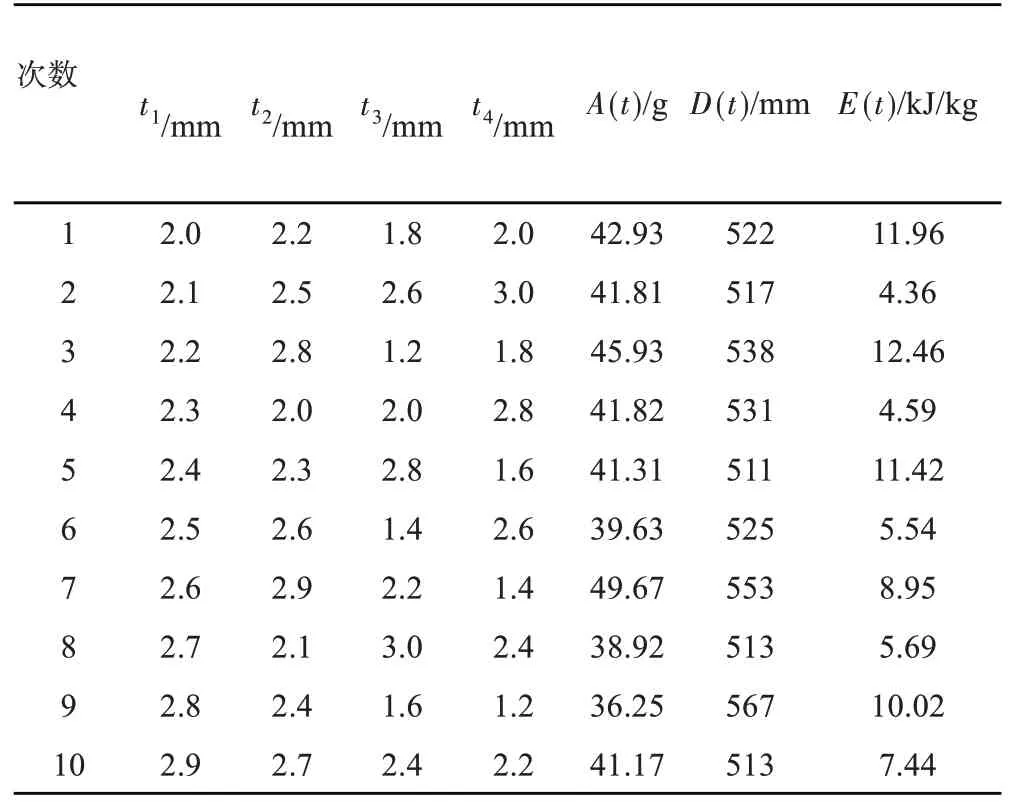
表2 均匀设计试验表Tab.2 Uniform design test table

4.2 人工神经网络模型

建立人工神经网络模型的目的是拟合车辆耐撞性模型的输入与输出，与其他形式的响应面法相比，人工神经网络能够表现出很好的柔韧性。这里采用具有一层输入层、一层隐含层以及一层输出层的三层神经网络来拟合，其中隐含层的传递函数是“logsig”，输出层的传递函数是“purelin”。同时还随机挑选了10组测试数据来验证所建立的神经网络的泛化能力，这能避免所建立的神经网络能够反映车辆耐撞性的“共性特征”而不是所选10个样本点的“局部特征”，收敛精度设定为1×10-5。

如图7所示，预测值与测试数值模拟值能够保持一致，表明所建立的神经网络模型能够很好的反映车辆耐撞性问题的输入与输出之间的关系。

图7 仿真结果与模型预测结果对比Fig.7 Comparison of Numerical Results

5 耐撞性优化

5.1 问题阐述

由于车辆耐撞性优化评估指标包含最大峰值加速度A(t)，B柱最大位移D(t)以及吸能比E(t)，属于多目标优化问题。约束条件以吸能盒上板厚度、吸能盒下板厚度、前纵梁加强板厚度以及前纵梁U型板厚度取值范围为边界，取值情况如表1所示。最终建立的多目标优化函数如式（1）所示。

传统多目标优化问题通常是通过引进权重系数将其转化为一个单目标优化问题，但权重系数的取值并没有统一方法，选值大小和设计者之间紧密相关，这就容易导致不同的设计者之间的优化结果差异较大。近年来，考虑遗传算法具有很好的全局寻优能力，研究者开始使用遗传优化算法来解决多目标优化问题，例如MOGA，NPGA，NSGA，SPEA，PAES and NSGA［15-17］.这里采用基于传统遗传算法发展起来的NSGA-Ⅱ算法，其主要依赖“快速无支配排序”以及“拥挤度排序”两大机制完成问题优化。

5.2 多目标遗传优化算法

如图8所示，为NSGA-Ⅱ多目标遗传优化算法流程图。首先根据传统遗传算法产生一个数量为N的初始父代随机种群P0，通过选择、交叉以及变异炒作，得到一个数量为N的子代种群Q0。将父代子群P0与子代种群合并得到一个数量为2N的新种群，采用“快速无支配排序”法对其编序，如F1、F2等。

图8 NSGA-Ⅱ流程Fig.8 NSGA-ⅡProcedure

将排序处于前N的解全部选入P1，其余解抛弃，这种排序法就叫做“拥挤度排序”。新的规模为N的种群又会开始下一轮“快速无支配排序”以及“拥挤度排序”操作［16］，最终得到一组最优Pareto解集。

5.3 优化结果与分析

如表3所示，是优化后得到的最优Pareto解集，由于Pareto解集是对各目标函数折中后的一组最优解集，因此没有任何一组解可以视为整个问题的最优情况。例如，如果设计者对最大加速度比较关注，则3、4以及6组比较适合作为最优解。如果设计者对吸能比比较关注，则2、14以及15组比较适合作为最优解，设计者也可以综合考量三个因素。以6组为例，此时吸能盒上板厚度为2.0mm，吸能盒下板厚度为2.1mm，前纵梁加强板厚度为2.9mm，前纵梁U型板厚度为1.7mm，最大峰值加速度减少了2.4g，B柱最大位移从523mm减少到506mm，吸能比从12.70减少到12.4，这表明在吸能比减少轻微的情况下，乘客的安全性可以大幅增加。

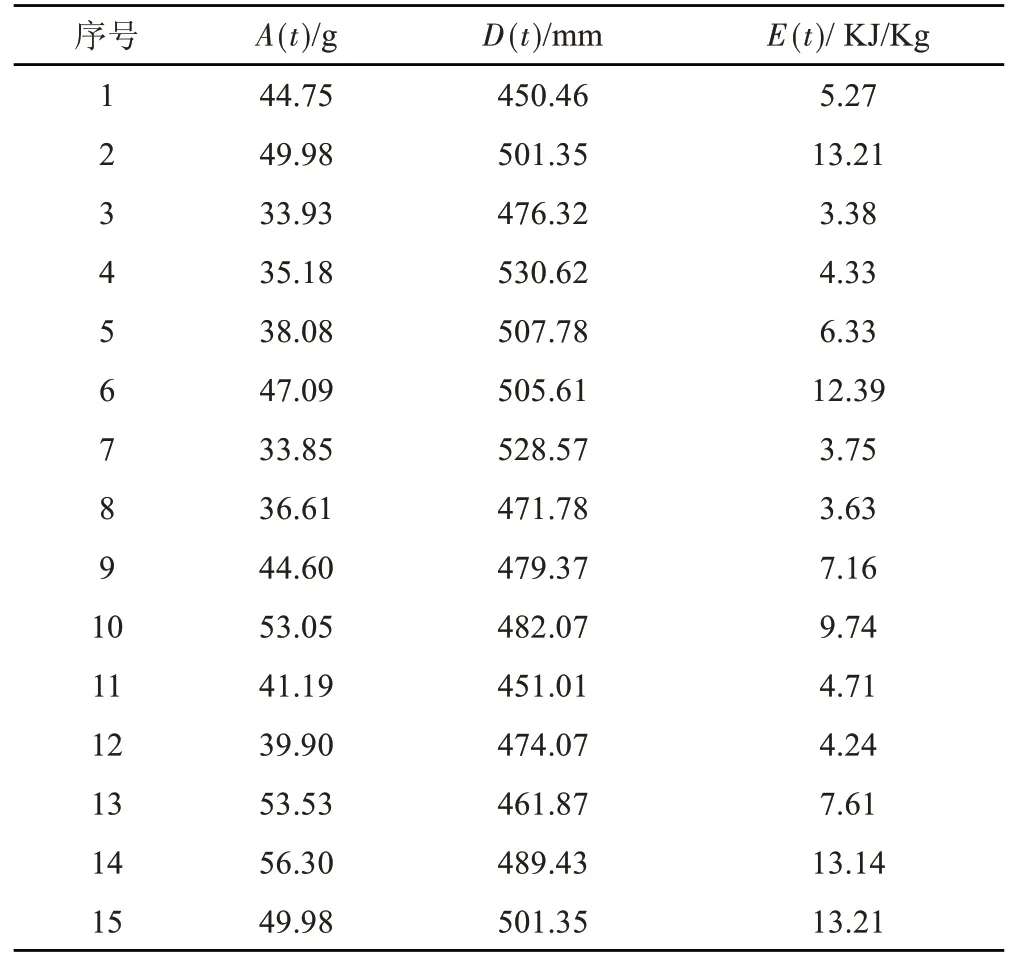
表3 Pareto解集Tab.3 Pareto Solution Set

6 结论

（1）与试验结果相比，建立的车辆耐撞性模型具有非常高的精确度，能够用来进行车辆耐撞性研究。（2）采用均匀设计法进行样本点的选择，可以减少仿真模拟次数，提高优化效率，建立的三层神经网络能够精确地拟合车辆耐撞性的输出与输入。（3）根据NSGA-Ⅱ得到的车辆耐撞性优化结果显示这里提出代理模型能够很好地实现车辆耐撞性优化，所提方法能在实际工程问题中节约大量的时间与物力成本。