数控机床大功率DC-DC转换器设计与控制

2021-10-20张淑艳张长春田纪亚

机械设计与制造 2021年10期

张淑艳，张长春，田纪亚，王超

（1.长春光华学院电气信息学院，吉林长春130033；2.吉林大学机械工程学院，吉林长春130033）

1 引言

随着我国装备制造业的快速发展，机床行业也面临着转型升级，与传统机床不同，数控机床内部包含有传感器、伺服电机等多个芯片，而每种芯片要求的电压也不相同。目前，大多采用DC-DC变换器对输入电源进行功率切换，精确得到芯片需要的供电电源［1-5］。因此，DC-DC变换器的设计与控制对数控机床的正常运行起到至关重要的作用［6］。

DC-DC变换器从诞生以来，一直备受电力电子界的青睐，从最基本的Buck、Boost、Buck.Boost、Buck／Boost双向变换器拓扑结构被提出后，专家学者们在此基础上相继派生出了多种DCDC拓扑结构，以弥补和扩大基本DC-DC变换器的工作性能。采用不同DC-DC拓扑结构可以降低系统能耗［7-8］，但其效率较低，电压阶跃比较低，高频变压器中的损耗较大。对于双有源电桥（DAB）DC/DC变换器，可利用软开关来减少能耗［9-11］，但其效率可能受到高频变压器的循环功率和核心损耗的影响。文献提出了隔离型双向DC-DC变换器的多种拓扑及控制策略［12-13］，但主要用于低压输入、高压输出且需要隔离的场合。文献设计了一种以超级电容加双向DC-DC变换器为辅助动力的方案，并分析其控制策略及模式切换策略，提高了系统的能源利用率［14］。文献提出LCL DC/DC转换器作为兆瓦级功率传输的高效率替代方案［15-16］，其基本的LCL拓扑包括两个电压源转换器及其之间的LCL谐振槽，通过使用电容器代替高频变压器并通过控制两桥之间的功率流来减少损耗，但它不允许高DC-DC阶跃比，也不严格限制LCL槽中电容器两端的电压。

针对数控机床行业中使用的大功率转换器，基于LCL两侧零无功功率和有功功率平衡的条件，设计一种LCL-DC/DC转换器以实现更高的电压阶跃比，对电容器电压进行严格限制，并采用基于P-Q理论的方法对LCL直流变换器进行控制。根据设计的转换器，在EMTP-RV软件中搭建仿真模型，并对仿真结果进行分析以验证设计方案的可行性。

2 转换器工作原理

提出的双有源桥及LCL转换器的工作原理，如图1所示。其基本拓扑结构包括两个电压源转换器和他们之间的LCL谐振槽。每个DC/AC桥连接到具有4个开关的内部LCL槽，作为电压源转换器工作，每个桥连接器都能够双向工作以实现可控功率的传递。设定终端1为源侧，终端2为负载侧。为了应用稳态分析和减少计算复杂性，给出一些假设：电容器C1和C2的电容足够大，直流电压V1和V2在调制周期中为常数，且所有的开关、二极管和LCL元件都是理想元件。

图1 双桥及LCL转换器工作原理Fig.1 Double Bridge and LCL Converter Working Principle

设计的主要目标是使转换器能够实现更高的电压阶跃比，限制电容器电压，使其具有更高的性能以适用于大功率数控机床的正常工作。对该转换器的特性进行分析并对其各元件参数进行设计。

3 转换器特性分析

3.1 频率特性

为方便分析，用两个与LCL谐振槽连接的脉冲电压源表示两个电压源转换器，可得到LCL转换器的等效图，如图2所示。

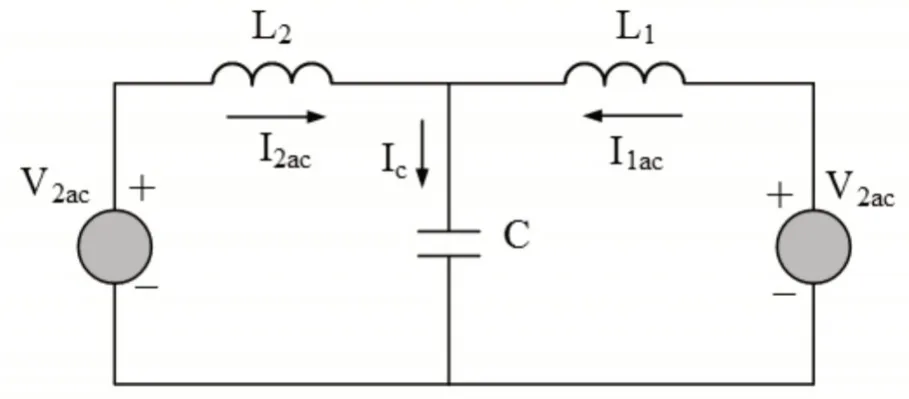
图2 LCL转换器等效原理图Fig.2 LCL Converter Equivalent Schematic Diagram

通过从两个脉冲电压的傅里叶级数展开式中提取基本分量，可得到线路中性电压幅度的峰值为：

式中：β1、β2-图2中的传导角度，这些角度可以表示为：

式中：Ma1、Ma2-控制信号的幅值。考虑到只有基本的交流分量，可得到：

为便于控制，借鉴空间向量分量的思想，引入所有相量的正交分量。将坐标系与向量V2ac对齐，可以得到：

式中：k1=1-ω2L1C，k2=1-ω2L2C，k3=L1+L2-ω2L1L2C，可以得到LCL转换器的三个谐振频率分别为

式中：frmain-LCL变换器的主谐振频率；fr1、fr2-局部谐振频率。

3.2 功率特性

在考虑系统的功率特性时，将零无功功率和有功功率平衡作为设计的条件分别进行分析。

3.2.1 无功功率

将零无功功率条件应用于LCL电路的两端时，电路的工作电流最小，可降低开关损耗。此时，负载侧的零无功功率使其电流的q分量为零，因此表现出具有有效电阻R2的电阻负载。由此可得

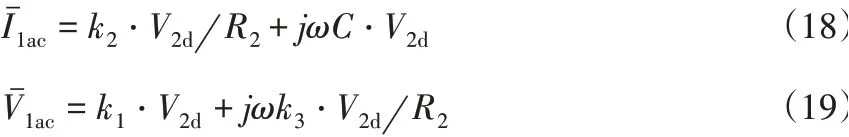
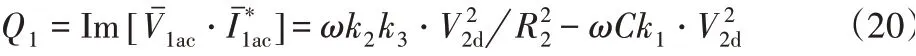
对于给定的开关频率，当L1、L2和C确定之后，转换器低电压侧的有效电阻R2是恒定的。在此条件下，可得到零无功功率条件下LCL电路的向量图，如图3所示。

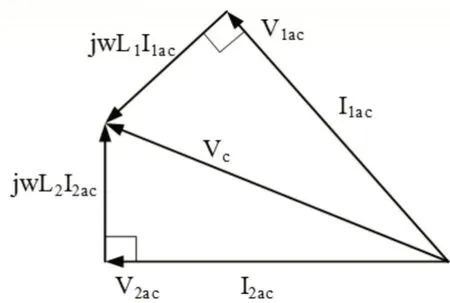
图3 零无功功率条件下LCL电路向量图Fig.3 Vector Diagram of LCL Circuit under Zero Reactive Power Condition

由图可得到两个交流电压源之间的相移为

联立可得

由上式可得，给L1、L2、C和ω之后，两电压之间的相移是固定的，k1和k2符号相同且必须满足0＜k1k2≤1。

3.2.2 有功功率

对于有功功率，需要满足功率平衡的条件。在零无功功率的条件下，可以得到两侧有功功率的表达式。

式中：R1、R2-两侧的等效电阻。通过有功功率平衡条件和公式（1）（2），可得到

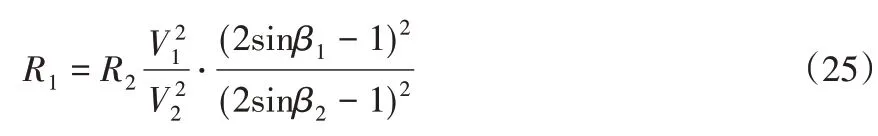
3.3 电压特性

3.3.1 电压阶跃比

定义电压阶跃比为转换器两侧的直流电压之比，可表示为

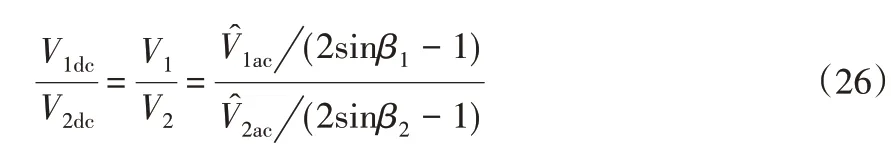
联立可得

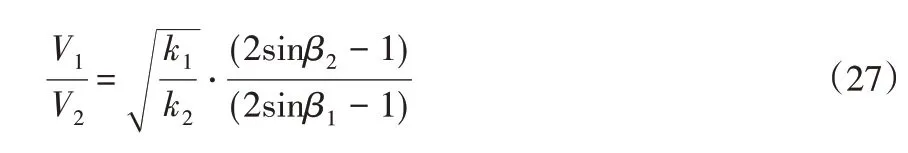
当β1=β2=90o时功率转换效果最大，此时

上式表明，k1、k2符号必须相同，且对于降压转换器，k1＞k2，而且，转换器的开关频率ω必须小于主LCL谐振频率。对于（15）和（16）给出的局部谐振频率，转换器开关频率可以高于2πfr1和2πfr2，也可以低于2πfr1和2πfr2。据此，可分为前共振情况和后共振情况。

对于前谐振情况，k1，k2均为正值且小于1，若取较高的电压阶跃比，例如当取阶跃比为20，即时，若k1=0.1，则k2=0.00025，k2的值太小，敏感性较高。当L2C的值产生很小的变化时，可能使得ω2L2C＞1，导致系统的不稳定。如取k1=0.95，k2=0.05，得到的阶跃比为4.2，即使通过改变β1的范围，使得2sinβ1-1=0.5，可得到的阶跃比为8.4。

对于后谐振情况，k1，k2均为负值，则k2=-0.05，k1=-20时，得到的阶跃比为20，且这两个值均为有效值，不会引起系统不稳定。综合上述分析，在后谐振情况下可以实现更高的电压阶跃比，因此选择这种情况作为这里转换器设计的方案。

3.3.2 电容电压

LCL槽的电容C是LCL变换器的关键元件之一，因此，应尽可能保持其电容和电压的成本效益。联立公式可得：

因此，电容C可用其最大值进行表示：

计算得到的电容电压为：

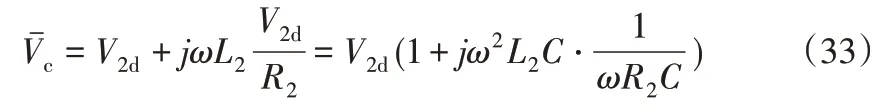
联立可得：

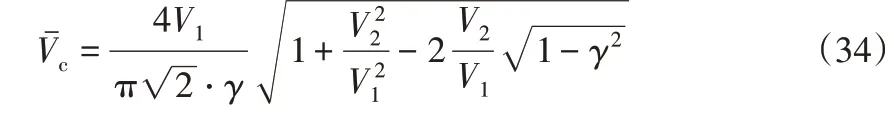
通过上式可得，可采用参数γ来表示参数k1，k2和电容电压的幅值，在设计过程中，将参数γ作为重要的设计参数使用。

4 控制策略设计

4.1 设计流程

这里设计的主要目的是实现期望的阶跃比，限制电容器电压，并实现变换器稳定的工作。这需要在多个目标中折衷选择较优的条件。根据之前引入的设计参数γ，可以得到一些参数与参数γ之间相关性的函数。k2，Vc与γ之间的关系，如图4所示。由图可知，随着γ的增加，电容电压逐渐减小，这与期望的趋势一致。而随着γ的增加，电容C的值也会与γ成比例地增长。另外，当γ趋近与1时，k2的绝对值变得非常小，此时电压阶跃比对L2和C的很小的变化也会有很高的灵敏度，会极大的增加系统的不稳定性。

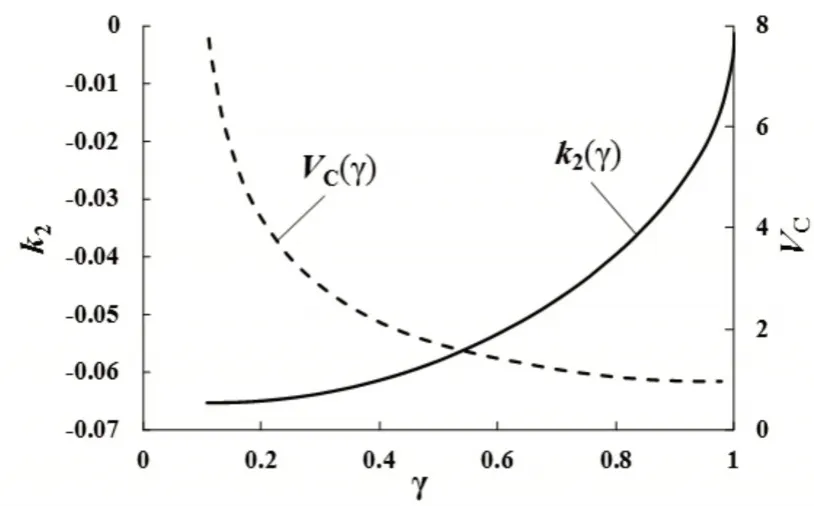
图4 k2，VC和γ之间的关系Fig.4 Relationship of Three Variables k2，VC，γ

3个谐振频率与γ的关系，如图5所示。随着γ趋近于1，局部谐振频率fr1和fr2都快速接近变换器的开关频率。因此，为了保证系统的稳定性，排除γ＞0.9的范围。另一方面，过小的γ值将会导致高的电容器电压，并且会限制高的阶跃比。基于以上分析，可提出如下的转换器设计过程。

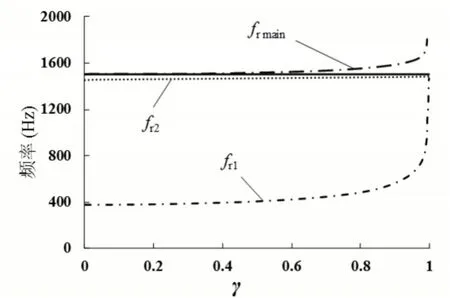
图5 谐振频率与γ的关系Fig.5 Relation between Resonance Frequency and Gamma

首先找到负载侧交流电压，然后计算负载侧电阻R2；根据图4，多次迭代以选择合适的γ值，使计算得到的C、VC值在可接受范围内；然后根据γ值，计算得到k1和k2；由此可根据下式计算得到谐振槽的电容C，电感L1和L2的值。

4.2 控制策略

在转换器的设计与控制中，控制策略的设计是至关重要的。为了保证零无功功率和有功功率平衡条件，采用的控制策略是基于瞬时有功和无功功率和P-Q理论，直接以有功功率和无功功率作为控制量进行操作。其中P-Q理论是将单相电压或电流转换90°以获得正交伪α、β信号。这里采用一种二阶广义积分器（SOGI）方法，其原理如图6所示。

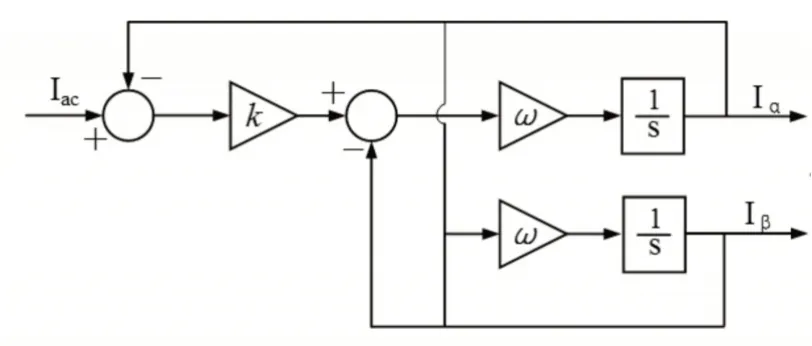
图6 SOGI方法原理图Fig.6 Schematic Diagram of SOGI Method

假设转换器一侧的有功功率和无功功率分别是Pd和Qd，并通过SOGI生成其正交分量Iα和Iβ，则可以通过P-Q理论计算产生这些Pd和Qd所需电压的α和β分量。

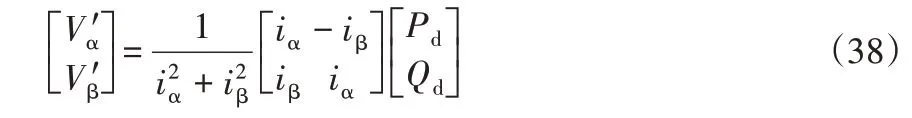
通过上式，可确定参考电压的幅值V′m，以及其相对于SOGI中参考框架的相移β′。

可利用这些值构成转换器桥接器的调制方案。两侧桥路分别采用相同的基于P-Q理论的控制模块。可得到基于P-Q理论的转换器控制方案原理，如图7所示。

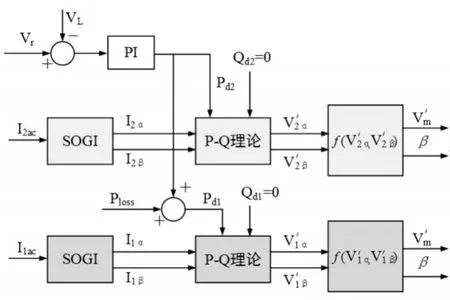
图7 基于P-Q理论的转换器控制方案原理Fig.7 Principle of Converter Control Scheme Based on P-Q Theory

通过零无功功率条件和有功功率平衡条件可得到完整的结构，且该原理中仅采用一个PI控制器，因此系统的稳定性较好，硬件更容易实现。

5 实验仿真分析

为了对设计的过程和方案进行验证，在EMTPRV软件环境中搭建了一个100MW 300kV/20kV LCL变换器，选择较大功率的原因，是考虑一个DC-DC变换器同时给加工车间的多个数控机床供电的工作情况。

根据分析和设计，我们选择γ＝0.65，此时k2、Vc、I1Sc和I2Sc的值分别为0.0507、1.32、1.17和1.54，都在较为合理的范围之内。这里提出的LCL转换器的仿真参数，如表1所示。

表1 LCL转换器仿真参数Tab.1 LCL Converter Simulation Parameters

设计方案的仿真结果，如图8所示。图中所有电压都是由从导线到中性点的值表示。转换器2侧功率的响应特性，如图（a）所示，到达稳态的时间为0.2s，最大超调量为0.1，无较大波动，响应速度较快且稳定性好。电容电压特性如图（b）所示，由于LCL谐振槽可起到交流变压器的作用，故电容器电压具有正弦波形，波形幅值约为600kV，周期约为0.7ms。转换器1侧与转换器2侧的电流和电压特性图，分别如图（c）和图（d）所示，转换器1侧电流幅值为0.5kA，电压幅值为150kV，而转换器2侧的电流幅值为7.5kA，电压幅值为10kV，两者频率相同，但由于有功功率是从转换器1侧传递至2侧，因此Iˉ2ac相对于电压Vˉ2ac具有180°的相移，两侧的零电流开关使得开关上的应力最小。另外桥1的电流和电压、Vˉ1ac和Iˉ1ac的交流电压和电流彼此同相。由图可知，按照所提出的方法设计的转换器，在90°导通角的两端都处于稳定状态，能够实现高的电压阶跃比并限制电容器，响应速度较快且具有稳定的运行特性，可用于数控机床中大功率高阶跃比DC-DC转换器设计与控制。