一种分析伺服进给系统动态误差的新方法
2021-10-20赫巍巍王立平关立文李大奇
赫巍巍,王立平,关立文,李大奇
(1.东北石油大学机械科学与工程学院,黑龙江 大庆163318;2.吉林大学机械与航空航天工程学院,吉林 长春130022;3.清华大学机械工程系,北京100084)
1 引言
伺服进给系统是数控机床的重要组成部分,是连接数控系统CNC和机床主体的关键[1][2]。因此,伺服进给系统的性能优劣是影响数控机床加工效率以及加工工件表面质量和精度的主要因素,所以研究伺服进给系统的动态误差对于建立机床动态误差理论研究框架具有十分重要的意义[3-5]。
目前对于机床伺服进给系统的研究有很多,文献[6]建立了交流伺服进给系统下的XY工作台的数学模型,并基于该模型,研究了改变间隙、摩擦等因素后对工作台性能的影响,并将其应用于摩擦补偿中,便于提高系统的精度。文献[7]建立了数控机床伺服进给系统的数学模型,推导了其传递函数,并通过仿真得到系统参数与伺服系统性能之间的关系,为改善和提高数控机床伺服系统的性能,提供了一些可靠的理论依据。文献[8]以龙门机床主轴进给驱动为研究对象,利用虚拟样机技术建立其多体动力学模型,确定了丝杠、滑枕柔性和导轨-滑块结合面参数,构建了主轴进给模块刚柔耦合模型,并在MATLAB/Simulink中建立了永磁同步电机矢量控制模型,从而建立了龙门机床主轴进给驱动刚柔-机电耦合仿真模型,并对三环PID参数进行了整定。文献[9]建立了CK1416数控车床的进给系统模型,构建了包括刚度、非线性间隙和非线性摩擦的参数化结构。文献[10]建立了CK78158数控机床伺服进给系统的模型,并根据仿真模型分析了间隙、死区等非线性因素对系统精确度的影响。文献[11]以五轴机床运动产生的弹性变形为出发点,建立了A/C双摆头机床进给系统动力学模型,推导了因进给系统弹性变形导致的轮廓加工误差,并基于S试件,给出了其数控加工过程的运动控制策略,分析了轮廓度误差与试件曲率间的关系,得到了数控机床进给系统刚度特性对自由曲面轮廓误差的影响机理,同时文献[12]还建立了机械系统和伺服系统的模型,分析了导致S试件动态误差的动力学因素及其影响。
上述针对机床伺服进给系统的研究中,研究的基本思路为:首先搭建仿真模型,并尽量与实际模型相符合;然后改变仿真模型参数(例如间隙和PID控制参数)研究这些参数对仿真结果的影响;最后调节实际机床的此类参数,以验证仿真结果的有效性。这种研究思路属于定性探索。而这里提出的分析五轴机床伺服进给系统动态误差的新方法属于定量探索,为五轴机床以及其他动平台的动态误差研究提供了新思路,为后续研究五轴机床动态误差提供了基础理论支撑,对于提升我国数控机床研发能力和水平具有重要意义。
2 伺服进给系统模型
2.1 平动轴建模
伺服进给系统平动轴模型,如图1所示。图中:J1-主动轴转动惯量;J2-从动轴转动惯量;Tm-电机输出扭矩;θm-电机输出转角;T2-经过齿轮传动装置作用到从动轴的驱动扭矩;Th-从动轴驱动滚珠丝杠的输出扭矩;θh-从动轴驱动滚珠丝杠的输出转角;K2-从动轴的扭转刚度系数;D2-阻尼系数;Mt-动平台的质量;Dt-阻尼系数;Xt-位移;ft-所受负载阻力。第一级减速装置减速比为i,第二级滚珠丝杠减速比为ih,对于单线螺纹的滚珠丝杠ih=2π/Ph,其中,Ph为滚珠丝杠螺距。
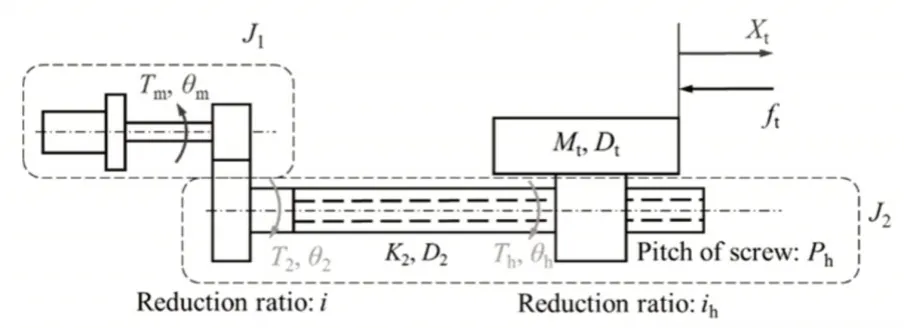
图1 平动轴模型Fig.1 Model of Translational Axis
将平动轴模型中的主动轴与从动轴的力矩平衡方程进行拉氏变换,得到系统的传递函数为:


Xt(s)受Ft(s)影响部分的传递函数为:
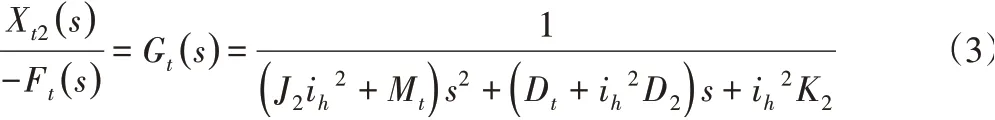
根据劳斯判据,两部分的系统皆稳定,因此两者综合的系统也是稳定的。最终可以得到平动轴系统模型为:
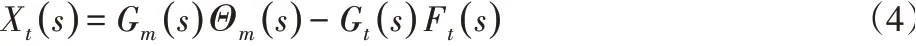
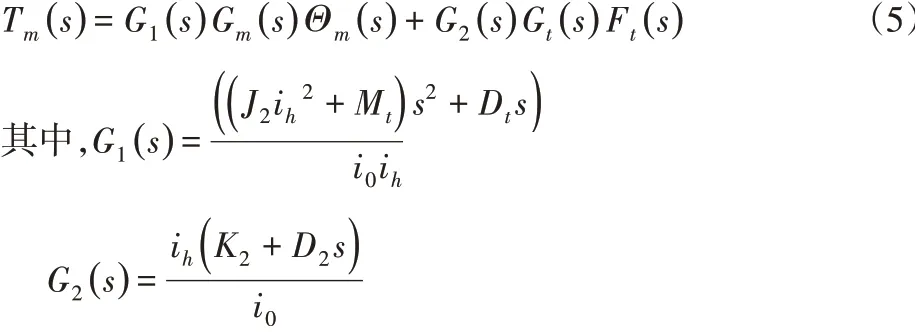
2.2 转动轴建模
伺服进给系统转动轴模型,如图2所示。动平台的转动惯量为Jt,转角为θt,所受负载阻力为Tt,第二级蜗轮蜗杆减速比为ih。

图2 转动轴模型Fig.2 Model of Rotary Axis
将传动机构的动力学平衡方程拉氏变换后可以得到转动轴系统传递函数为:

转动轴系统的数学模型表达式为:

其中,
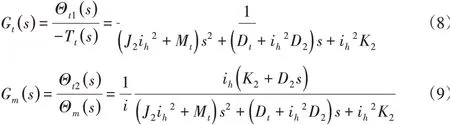
2.3 伺服系统建模
在五轴数控机床加工的过程中,大多数使用的电机为永磁同步交流电机(PMSM),而这里将使用直流电机的电流环等效为交流电机的电流环。将其等效的依据为:(1)PMSM的建模存在一个解耦的过程,并且控制参数的整定较为不便;(2)考虑到直流电机与交流电机的基本控制结构都是电流环、速度环、位置环,具有一定的相似性;(3)PMSM控制参数调节参考的是二阶系统的调节方式,而直流电机在不考虑控制的情况下,正是一个典型的二阶系统。
如图3所示,为电机的物理模型图。图中:ei(t)-电机电枢的输入电压;La-电枢电感;Ra-电枢电阻;em(t)-电机旋转时产生的反电动势;ia(t)-流过绕组的电流;T(t)-电机的输出转矩;θ0(t)-电机的输出转角;Je-电机轴的转动惯量;MC(t)-负载转矩。由动力学和电磁学等物理规律可以得到输入输出之间的关系,进而通过拉氏变换得到Θ0(s)受Ei(s)影响的传递函数为:

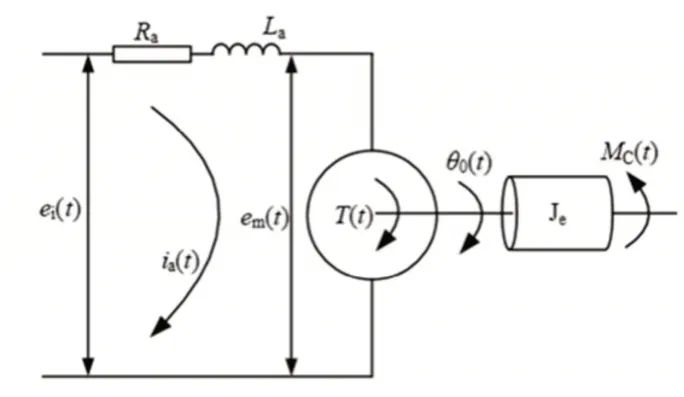
图3 电机模型Fig.3 Model of Motor
Θ0(s)受MC(s)所影响部分的传递函数为:

如图4所示为电机的控制模型,电机控制模型对应的有两个输入,即输入电压Ei(s)和负载力矩MC(s),输出为电机转角Θ0(s)。

图4 电机控制模型Fig.4 Model of Motor Control
考虑速度环得到的传递函数为:

其中,
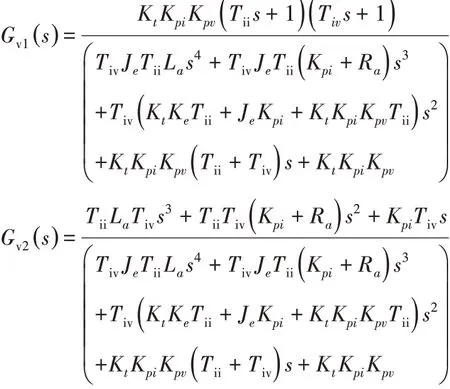
2.4 单轴机电耦合模型
伺服进给系统模型不能直接将进给模型和电机模型拼接在一起,否则会产生两个方面的问题:其一是仿真模型的代数环问题;其二是电机位置环的反馈信号检测问题。
针对第一个问题,可以将J1折合进入Je中,从而使得该代数环等效转化为非代数环,系统整体的传递函数和性质并未因此发生改变,由于不存在传动比关系,所以折合系数为1,即Je=Je+J1。同时电机模型中Je也不是原来的Je,而是加入了主动轴转动惯量J1的新Je,然后将J1记为0,即可避免在仿真时产生代数环。针对第二个问题,可以将伺服进给系统的位置环进行修改,即电机位置环的反馈信号改成检测平动轴或转动轴的最终位移。最终得到单轴机电耦合的仿真模型如图5所示:
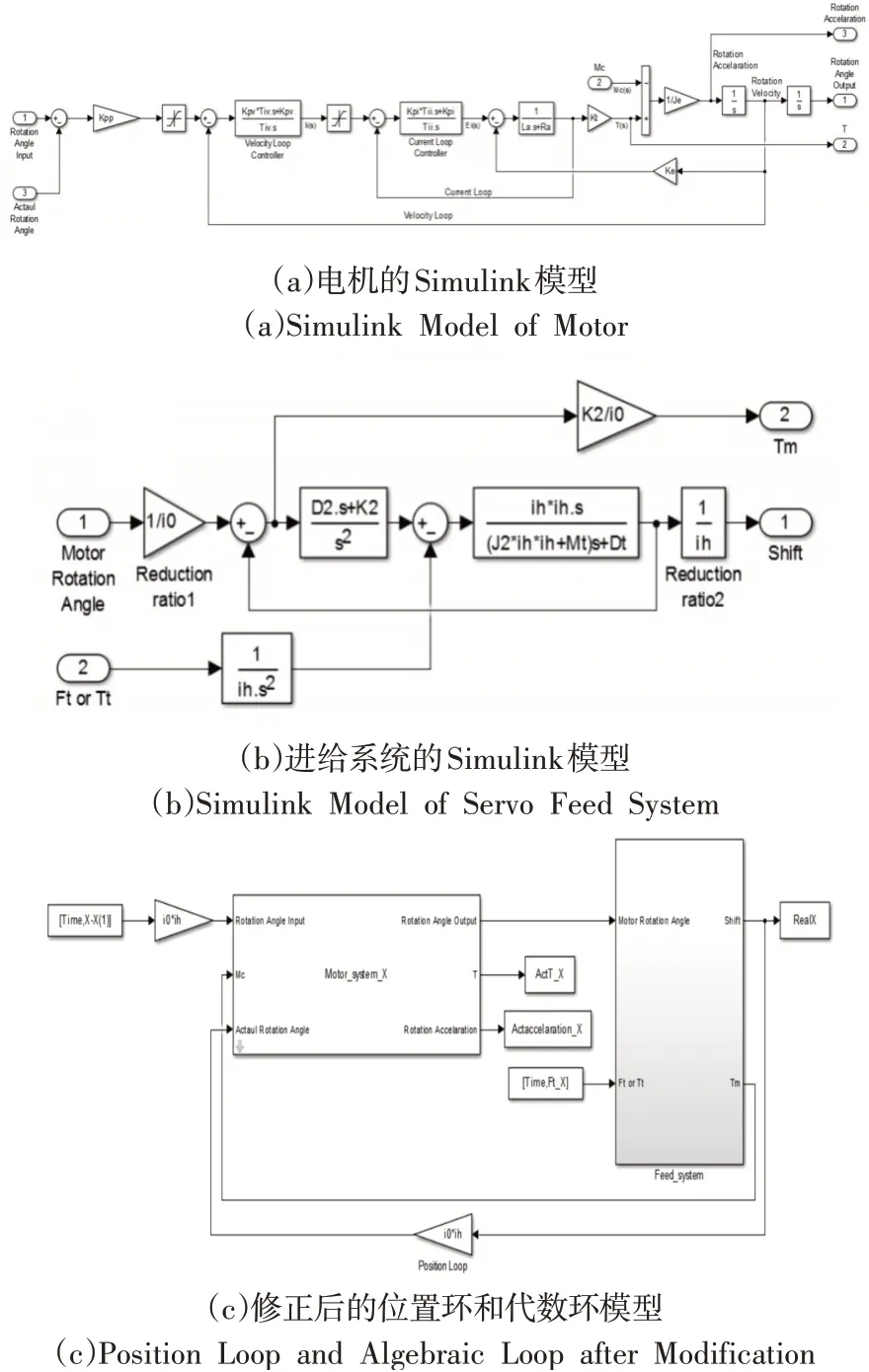
图5 单轴机电耦合模型Fig.5 Electromechanical Coupling Model of Single Axis
3 伺服进给系统动态误差分析的延时连续法
3.1 伺服进给系统的动态误差函数
由2.1和2.2节的分析可知,平动轴与转动轴的表达式在形式上是一致的,所以只需要分析平动轴即可类比至转动轴。根据平动轴伺服进给系统的模型可得:

其中,

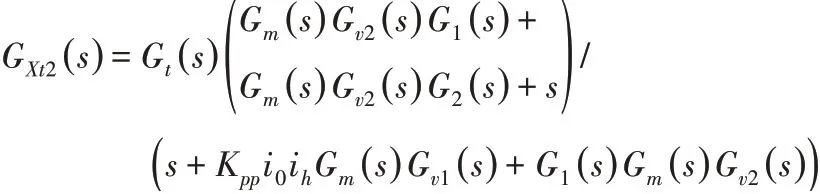
由此得到动态误差表达式为:
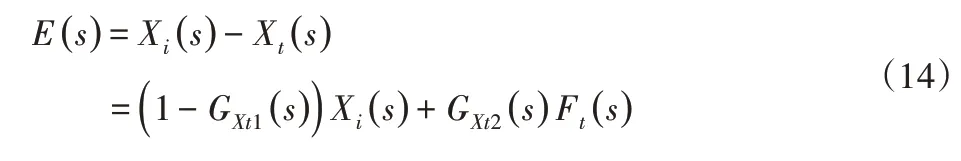
由上述推导的动态误差表达式可知,动态误差函数受两部分影响,一部分是输入另一部分是加工过程中的切削力其中受输入影响的部分为的表达式经过简化繁分数可得分子的部分为:

分母的部分为:
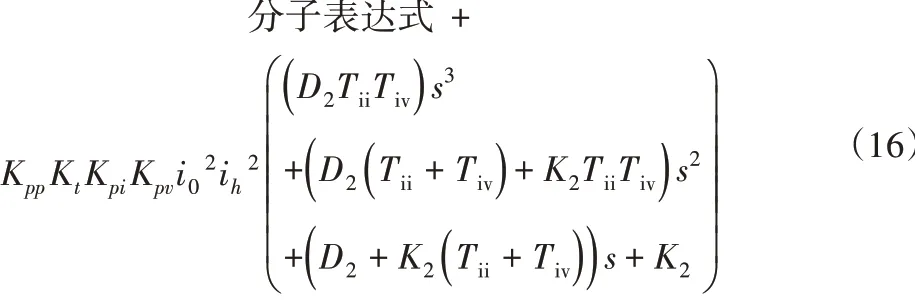
这里根据由沈阳第一数控机床厂提供的门式五轴加工中心VMC0656e的相关参数值,如表1所示。得到了高阶表达式的零极点图,如图6所示。

表1 伺服进给系统仿真参数表Tab.1 Simulation Parameter Table of Servo Feed System
图6中的偶极子总是可以相消的,因此可以得到:
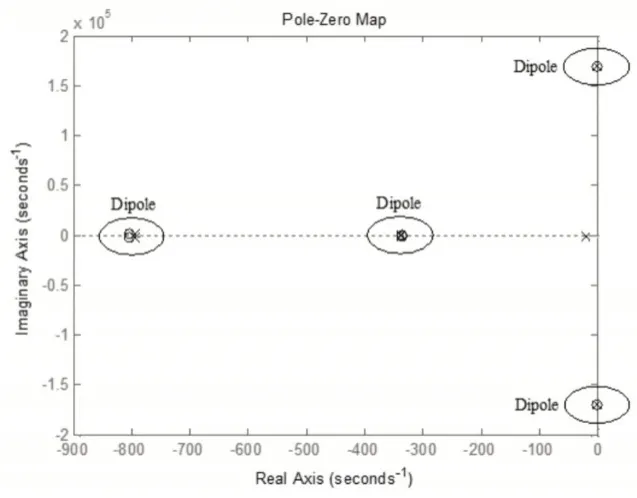
图6 零极点图Fig.6 Pole-zero Map

式中:参数u由系统特性决定,在这里给定的参数下,u=19.9794。将简化后的1-GXt1(s)带入(14),可以得到由输入引起的动

态误差表达式为:类似地,GXt2()s也可以用类似的方法进行化简,其反映的是切削力部分的动态误差,由于此部分不是这里的主要分析内容,故在此不多赘述。为了验证简化后的有效性,进行了两个实验,其一是单位阶跃响应(t=1s时阶跃)在简化前和简化后的动态误差图,如图7所示;其二是周期为1s的正弦响应在简化前和简化后的动态误差图,如图8所示。由图不难发现,在化简前和化简后的伺服进给系统的动态误差十分接近,即便时略有出入的地方,也相对于动态误差值而言可以忽略。所以将伺服进给系统动态误差受Xi()s影响的部分转化为s/s+u是完全可行的。
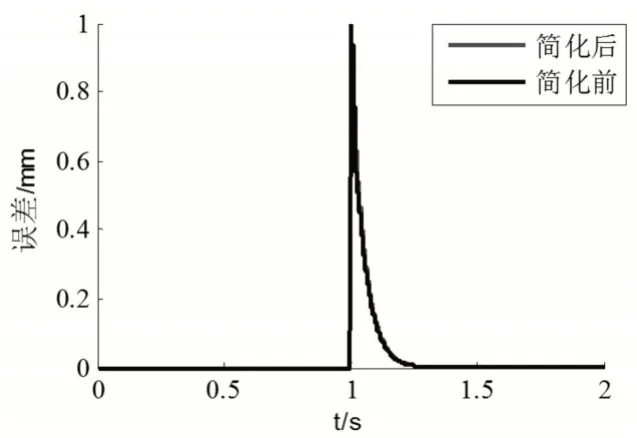
图7 单位阶跃响应在简化前和简化后的跟踪误差图Fig.7 Tracking Error Map of Unit Step Response before and after Simplification
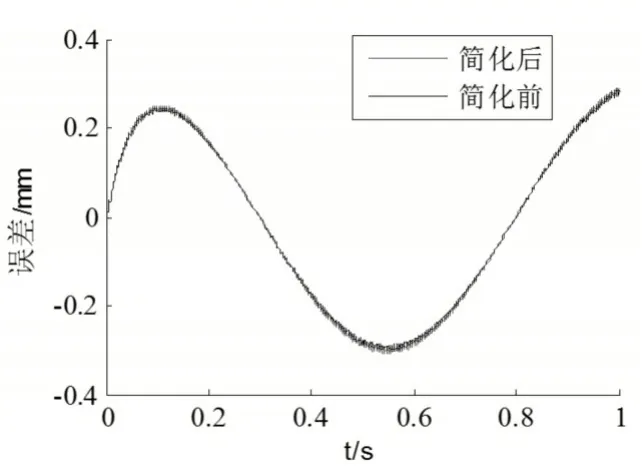
图8 周期为1s的正弦响应在简化前和简化后的跟踪误差图Fig.8 Tracking Error Map for Sinusoidal Response with Period 1s before and after Simplification
3.2 延时连续法的数学定义
通常的动态误差分析都是采用“搭建模型—改变模型参数—获取输出的动态误差”的形式来研究特定参数对于系统动态误差的影响程度,或者是采用终值定理的方式来分析稳态误差。对于机床或者自行搭建的动平台而言,采用第一种方法分析的确可以较好地达到设计参数的目的。
然而,如果要从理论上研究影响动态误差的因素,就必须试图获取带有数学解析形式的误差表达,第一种分析方法是无法获取这样的理论支撑的。由于存在伺服周期的原因,所以输入是离散的,可以将其看作是带有零阶保持特点的连续阶跃输入。如果将看成连续阶跃输入,可以写为如下形式:

根据拉氏变换的延时定理可得:

因此输入引起的动态误差为:
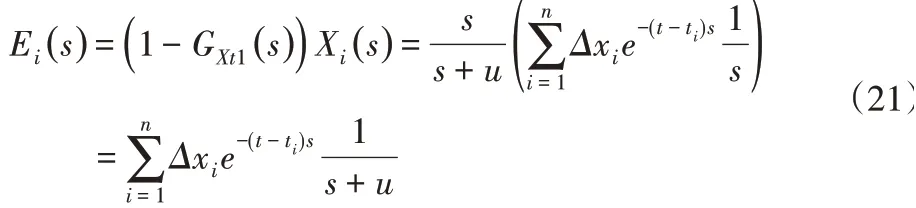
转化到时域上为:

上述将离散输入转化为延时阶跃输入形式的分析方法称为“延时连续法(DCM,Delay Continuous Method)”,最后可以得到系统动态误差关于输入的表达式(22)。该方法能够数学解析的表达动态误差,从而为理论分析动态误差提供支撑。推导过程为时域和频域的互相转化,整个转化过程不涉及近似处理,因而是绝对准确的。根据DCM方法得到的表达式,可以得出以下结论:
(1)式(22)中ti序列由伺服周期决定,在系统给定情况下,伺服周期通常是确定的。参数u由系统特性决定,在系统给定的情况下,仅仅能够通过调节PID的控制参数来调节u。因此在给定PID参数下,输入引起的动态误差仅取决于Δxi。试件若要有效地检测系统的动态误差,Δxi应当涉及一定的范围,并且与Δyi、Δzi、ΔAi、ΔBi、ΔCi形成多种多样的组合,从而可以确保加工任意其他零件都能够合格。
(2)一旦检测试件涉及了多种范围和多种组合,加工该试件后发生了超差现象,则在伺服周期无法改变的情况下,可以采取调节系统的控制参数,以达到将参数u调大的目的。如果反复调节机床控制参数仍不能取得较好效果,此时说明机床本身动态性能较差,在这种情况下,可以考虑降低进给速度,因为在G代码一定的情况下,线性插补后才获得每个伺服周期的位置指令,G代码一定,进给速度越小,则相邻两段代码之间的插补越密,从而插补出来的Δxi会偏小,进而降低动态误差。
(3)与G代码的疏密关系不大,G代码较疏时,特定进给速度下直线插补将会插补较多,G代码较密时反之,因此总体而言在G代码合理情况下差别不大,仅有的差别存在于疏密不同插补的点的坐标可能有所不同,但都是位于相邻两段G代码之间的线性区域,因此影响较小,可以忽略不计。
DCM方法在稳态时与终值定理得到的结论也基本一致,根据终值定理,接近稳定时s→0,因此:
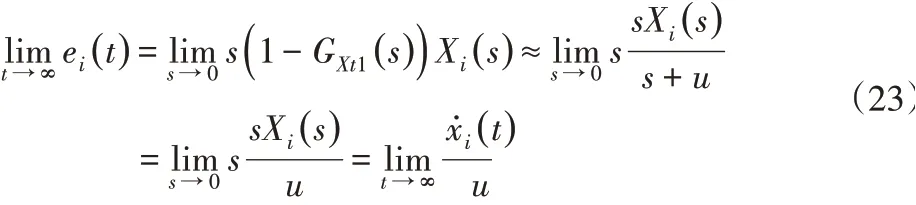
即输入引起的动态误差主要与输入速度项和参数u息息相关,输入是连续阶跃形式,因此其速度可以认为就是与Δxi正线性相关的一个量。而稳态误差与u负相关,也与DCM方法得出的结论吻合。
此外,DCM方法不仅在系统化简为一阶的时候可行,只要系统能简化成较为简单的形式,都可以用DCM方法推导,从而获得动态误差的解析表达式。
4 延时连续法有效性验证
DCM方法的推导过程在理论上是没有问题的,本节对推导结果进行仿真分析,以进一步验证DCM方法的有效性。通过对比分析仿真实验结果和理论推导得到的动态误差值,可以对DCM方法的有效性进行验证。
首先需要搭建DCM验证实验的Simulink仿真环境。在实际的五轴数控机床加工过程中,各个轴的伺服进给系统输入由不同的G代码的插补数据得到,一般伺服周期在4ms左右,调整时间大致为(20~100)ms之间。为了更好的还原实际加工中输入信号的各种连续阶跃形式,这里采用正弦函数作为实验的目标函数。给定输入的目标函数为然后假定伺服周期为4ms对该输入目标函数采样后作为实际输入[Time,X],其中Time为伺服周期采样的时间序列,X为采样后的输入值。如图9所示,为将离散输入转换成连续阶跃输入的示意图。同时设定传递函数为u/s+u,其中,u采用得到的数值19.9794。此时动态误差可以表示为sXi()s/s+u的形式,与上一节DCM方法推导时所使用的形式一致。Simulink仿真模型如图10所示,ei跟踪误差的时域输出。
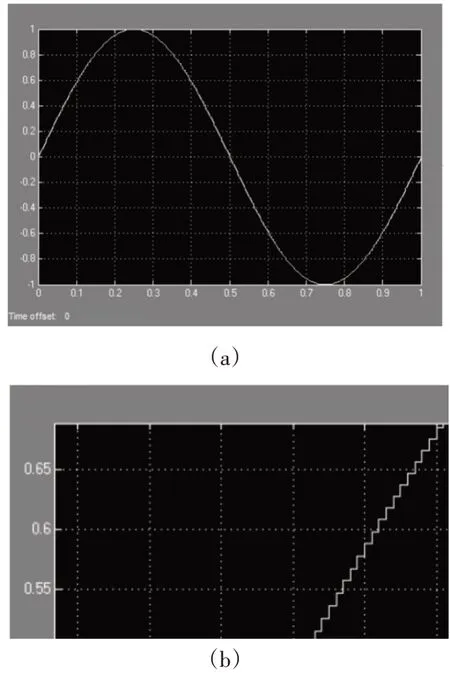
图9 DCM验证实验的连续阶跃输入Fig.9 Continuous Step Input for DCM Verification Experiments
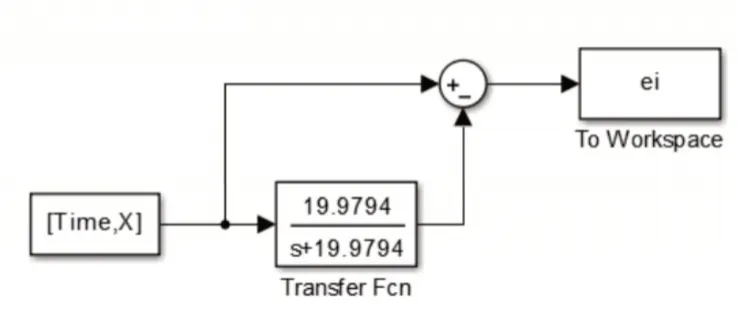
图10 DCM验证实验的Simulink仿真模型Fig.10 Simulink Model for DCM Verification Experiment
采用DCM方法推导的动态误差数学表达式直接计算出误差值,该实验输入为目标函数在伺服周期作用后产生的连续阶跃函数。如图11所示,可以看出Simulink仿真与DCM方法计算结果基本完全重合,在DCM方法的理论推导过程中未有任何的近似处理,因此理论上就应当完全重合,由此实验结果可以证明DCM方法的有效性。
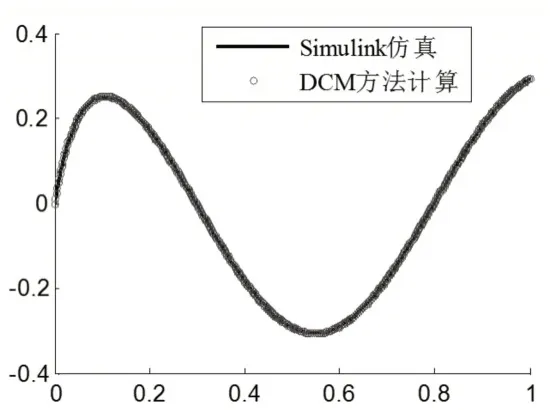
图11 Simulink仿真与DCM方法计算结果比较Fig.11 Comparison of Simulink Simulation and DCM Method
5 结论
(1)根据五轴机床进给系统的实际机械结构建立了进给系统的数学模型,同时用直流电机模型近似替代PMSM作为伺服系统的电机模型,从而构建了伺服进给系统的数学模型和Simulink仿真模型。
(2)基于建立的动态误差传递函数特性,对其进行偶极子相消,获得了简化形式的动态误差传递函数。基于这一简化的误差函数,提出了分析伺服进给系统动态误差的DCM方法。
(3)通过Simulink仿真实验验证了DCM方法理论推导的有效性。实验结果显示,Simulink仿真与DCM方法计算结果基本完全重合。
(4)提出的DCM动态误差研究方法可以建立进给速度、伺服周期和调整时间之间的数学关系,从而可以进一步建立模型的物理参数与上述因素之间的关系,达到建立动态误差研究理论支撑的目的,此外还可以用于插补方法和进给速度的选择研究。
