依据智能交通的PHEV自适应指数模型预测控制

2021-10-20胡丰宾

机械设计与制造 2021年10期

赵亮，胡丰宾

（1.山西机电职业技术学院，山西长治046011；2.北汽福田汽车股份有限公司，北京101100）

1 引言

随着能源危机、环境恶化和全球变暖等问题的加剧，使得新能源汽车成为汽车行业发展的主流，插电式混合动力驱车是我新能源汽车研究的主要方向［1］。对混合动力汽车实施合理高效的控制，可以有效减少使用成本和环境污染。

当前混合动力汽车的能量管理策略可分为三类：基于规则、基于全局优化、基于实时优化的能量管理。基于规则的管理方法控制简单，能够应用于实时控制，但是规则的制定依赖于开发人员经验，且工况适应性差［2］；基于全局优化的管理方法包括动态规划、庞特里亚金极小值原理等，此类方法计算量大，且要求全局工况已知，因此不适用于实际应用，大多为其他控制方法提供最优参考［3，4］；基于实时优化的管理方法包括等效燃油消耗最小［5］、模型预测控制［6，7］等，此类方法优点是可以实现车辆的实时控制，缺点是只能实现分时段的最优，难以实现全局最优。

这里研究了插电式混合动力汽车的经济性控制问题，使用智能交通系统获取整体路况信息，基于DP算法规划出预测时域内SOC参考轨迹；提出工况自适应指数模型预测方法，预测车辆状态和转矩需求，使用模型预测控制方法跟踪参考SOC轨迹并实现使用成本最低。

2 PHEV动力系统建模

2.1 插电式并联混合动力系统

这里研究对象为插电式并联混合动力系统，如图1所示。动力源包括发动机和ISG电机，ISG电机工作模式分为电动机和发电机两种。ISG电机与发动机同轴，两者之间设置主离合器，通过控制主离合器的开闭实现不同工作模式的切换。

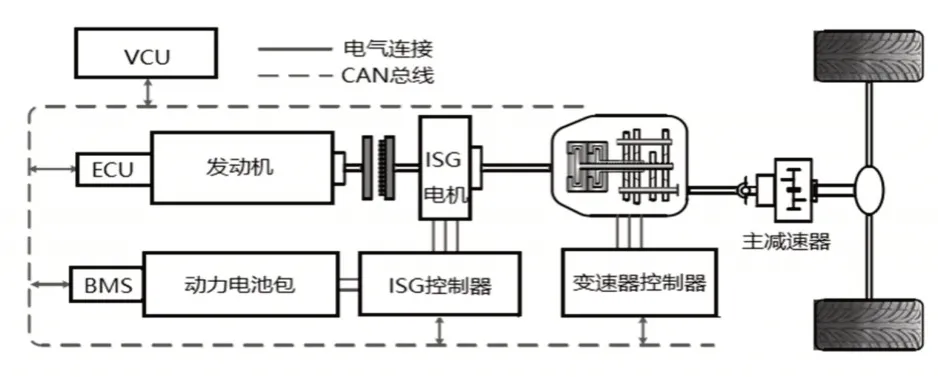
图1 插电式并联混合动力系统Fig.1 Plug-in Hybrid Power System in Parallel

混合动力系统的工作模式包括纯电动、发动机驱动、混合驱动、行车充电和再生制动等，各工作模式下关键部件工作状态，如表1所示。

表1 不同模式下关键部件工作状态Tab.1 Working Status of the Key Components for Different Working Model

2.2 关键部件建模

在此建立发动机、ISG电机、蓄电池模型，为车辆的经济性控制提供模型支撑。

（1）发动机模型。使用实验建模法建立发动机模型，依据发动机稳态实验数据，通过数值插值建立发动机模型为：

式中：Hu=46000kJ/kg-汽油热值常数。

（2）ISG电机模型。使用数值查表法得到电机模型为：

式中：ηm-电机工作效率；Tm-电机转矩；nm-电机转速；ψ2-查询函数。

（3）蓄电池模型。根据电池等效电路Raint模型，电池电量与输出功率的换算关系为：

式中：S(t)-t时刻SOC值；Ub-电池开路电压；Rb-等效内阻；Pb-电池输出功率；Qb-电池容量。

3 带SOC参考轨迹的模型预测控制

3.1 基于模型预测控制的PHEV能量优化方法

对插电式混合动力汽车使用带SOC参考轨迹的模型预测控制方法，控制原理，如图2所示。

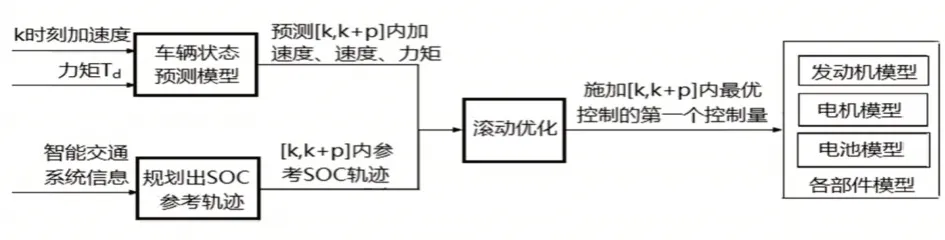
图2 PHEV模型预测控制原理Fig.2 PHEV Model Predicting Control Principle

带SOC参考轨迹的模型预测控制原理为：依靠智能交通系统获取出发点到目标点的实时路况信息，滚动规划出预测时域内的最优SOC轨迹；建立车辆状态的自适应指数预测模型，预测车辆的加速度、速度及转矩需求；根据SOC参考轨迹和车辆预测状态，建立优化目标函数，并获得最优控制向量；将第一个最优控制量施加在车辆上，实现车辆的经济性最优控制。通过以上原理可以看出，这里需要解决三个问题：（1）自适应指数预测模型的建立；（2）依据实时交通信息，参考SOC轨迹的规划方法；（3）滚动优化目标函数及约束条件的建立。以上三个问题中，参考SOC轨迹的建立方法篇幅略长，将在第4节中介绍。

3.2 工况自适应指数预测模型

车辆状态预测模型包括指数预测模型和马尔科夫模型等，文献［8］指出指数预测模型的精度优于马尔科夫模型，因此这里使用指数预测模型预测车辆加速度，进而预测出车辆速度和转矩需求，即

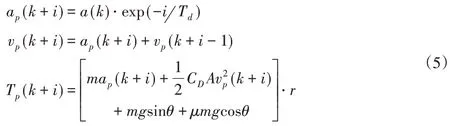
式中：ap(k+i)-由k时刻加速度a(k)预测的k+i时刻加速度，Td-衰减因子；vp(k+i)-由k时刻速度预测的k+i时刻速度；Cd-空气阻力系数；A-受力面积，m-车辆质量；g-重力加速度；θ-地面坡度；μ-地面摩擦系数；r-车轮半径。

式（5）中，车辆状态及转矩需求的预测精度取决于衰减因子Td的设置，当预测时域内车速变化缓慢时，车辆处于平稳驾驶模式，应设置较小的Td值；当预测时域内车速变化剧烈时，车辆处于激进驾驶模式，应设置较大的Td值。为了提高车辆状态预测精度，这里提出了驾驶工况自适应指数预测模型，具体原理为：选择工况识别特征参数，使用支持向量机对工况类型进行识别，根据驾驶工况自适应地调整Td值。

特征参数的选择是工况识别的关键，需要选择能够敏感不同工况特征的参数，结合指数预测模型特点，选择与车辆速度、加速度相关的10个参数作为特征参数，分别为：车速平均值及最大值、加速度平均值及最大值、减速度平均值及最大值、怠速时间比、匀速时间比、加速时间比、减速时间比。选择10种标准驾驶工况作为识别模式，分别为市区拥堵工况、高速公路行驶工况、城郊行驶的NYCC、New York Bus、FTP、ECE-EUDC-LOW、LA92、UDDS、US06-HWY、HWFET等工况，在1到10范围内寻找每种驾驶工况的最优衰减因子，并将驾驶工况按照最优衰减因子大小排序确定为1-10共10类工况。使用多分类支持向量机作为分类算法［9］，以120s工况块作为工况识别单元，使用复合等分法将各循环工况分割成120s工况块。使用140个样本数据对多分类支持向量机进行训练和测试，任意选取125个样本数据进行训练，其余15个样本数据用于测试，共进行5次实验，每次实验对测试样本的识别准确率均为100%，说明针对驾驶工况识别问题，这里选取的特征参数和识别方法有效，其中一次对测试样本识别结果，如图3所示。

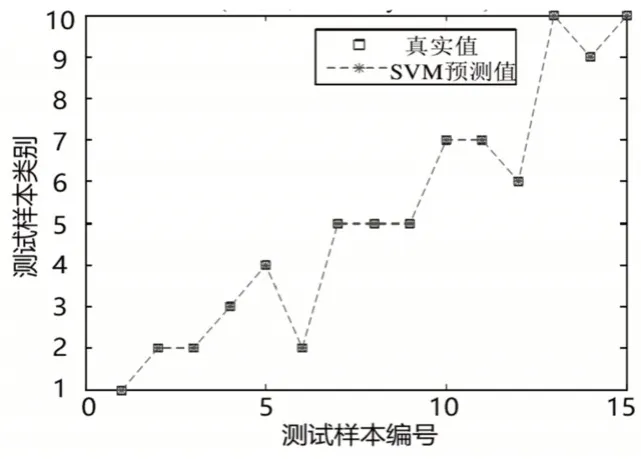
图3 驾驶工况识别结果Fig.3 Driving Cycle Recognition Result

构建由多种基本驾驶工况组成的综合循环工况，使用支持向量机对每个120s工况块进行识别，从而确定相应的最优衰减因子，综合循环工况的识别结果，如图4所示。

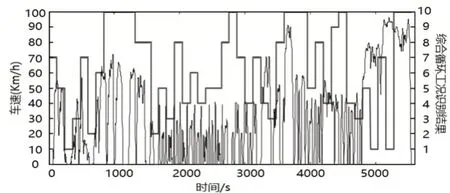
图4 综合循环工况识别结果Fig.4 Recognition Result of Comprehensive Driving Cycle

分别使用固定衰减因子和自适应衰减因子指数预测模型对图4所示综合循环工况的速度进行预测，使用固定衰减因子的预测方均根误差为2.132m/s，使用自适应衰减因子的预测方均根误差为1.046m/s，证明了自适应衰减因子指数预测模型具有更高的预测精度。

3.3 滚动优化目标函数

相比于传统混合动力汽车，插电式混合动力汽车具有更大的电池容量，且电量可以从电网中获得，因此可以实现更低的使用成本，k时刻使用成本为：

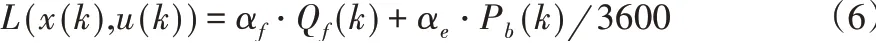
式中：x(k)-k时刻状态，定义为k时刻SOC值；u(k)-k时刻控制量，定义为k时刻发动机转矩Te(k)和k时刻档位ig(k)；αf=7.8元/升-汽油单价；Qf(k)-k时刻燃油量；αe=0.52元/度-每度电价格；Pb(k)-k时刻充放电功率。

记预测时域为p，则预测时域内的汽车使用成本为：

由于用电成本远远小于用油成本，若单纯以式（7）为滚动优化目标，则汽车在预测时域内会优先使用纯电动模式，导致电池SOC值下降过快，待SOC值下降至设定值时便维持电量，这种情况下带SOC参考轨迹的模型预测控制退化为混合动力汽车的CDCS模式，失去了滚动优化的意义。为了解决这一问题，将对每一时刻SOC参考轨迹的跟踪添加到目标函数中，即

式中：h(S(t))-对参考SOC跟踪的约束函数，其定义为：

我们的研究中，中国种子植物属的地理成分分布格局与中国植被和植物区系区划比较匹配，热带分布属占总属数80%以上的区域与中国分布的热带雨林及东南亚性质的热带植物区系分布区域比较符合，并且在该区域具有典型的热带分布科，该界线也与世界植物区系分区的泛北极或东亚植物区系与古热带植物区系的分界线相一致。

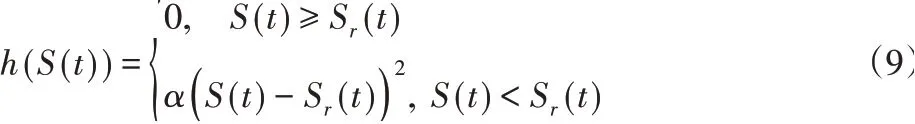
式中：S(t)-电池实际的SOC值；Sr(t)-电池的参考轨迹；α-极大正值，当电池电量被过度消耗时将产生极大的惩罚。由上式可以看出，滚动优化目标函数的这种设置方法可以有效地将电池SOC值限制在参考轨迹上方，防止电池电量下降过快，实现电能在整个行程中的均匀分配。滚动优化的约束条件为：

式中：Smin、Smax-预测时域[k,k+p]内的最小值和最大值；ne(t)-发动机转速，nemin、nemax-发动机最小和最大转速；Te(t)-发动机输出转矩，Temin、Temax-发动机最小和最大转矩；nm(t)-电机转速，nmmin、nmmax-电机最小和最大转速；Tm(t)-电机输出转矩，Tmmin、Tmmax-电机最小和最大转矩；Tb(t)-制动转矩；ig-档位，imax=6-最高档位。

3.4 求解最优控制量

在预测时域k～k+p范围内，以式（5）为预测模型，以式（8）为优化目标，以式（10）为约束条件，求得最优控制序列为将最优控制第一项u(k)施加于车辆动力系统，而后时间滚动到k+1时刻，重复以上步骤，直至车辆到达目的地。

4 SOC参考轨迹规划方法

4.1 实时交通信息获取与处理

智能交通系统（Intelligent Transport System，ITS）通过基础交通设施（摄像头、测速仪等）获取道路的实时交通信息，为个体用户提供出行信息和建议，是世界范围内的研究热点。将ITS应用于PHEV经济性控制的方法为：使用ITS获得同一路段同一时段的浮动车流量信息，将车流量信息通过路网传感器发送至信息服务器，而后提供给混合动力汽车个体用户，用户对车流量信息进行处理，得到SOC规划需要的车速-时间信息。

以重庆大学至长安福特间的路线为例，途经杨公桥、内环快速、机场路等，整个行程长26.3km，以300m为一个路程单位将全程划分为87个路段，统计每个路段过去5min内通过的车辆数和车速信息，则此路段的车速定义为：

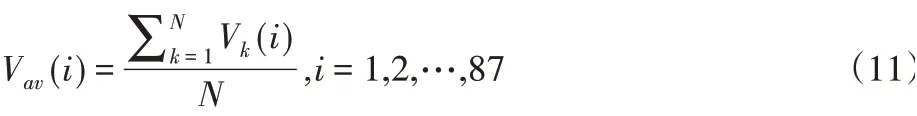
式中：Vav(i)-第i个路段的车速；Vk(i)-第i个路段第k辆车的车速；N-路段i在过去5min内通过的车辆数。

使用路段长度除以路段车速Vav(i)，得到通过路段i的时间，从而可以获得从出发点到目标点的车速-时间曲线，但是全程的车速信息分段计算得到，因此车速-时间曲线是阶跃型曲线，这里使用Lowess滤波函数对阶跃型曲线进行平滑处理，得到重庆大学至长安福特间的车速-时间曲线，如图5所示。

图5 实时交通信息处理结果Fig.5 Dealing Result of Real-time Traffic Information

4.2 预测时域内SOC参考轨迹规划

使用智能交通系统可以获取车辆从出发点到目标点的实时交通信息，若使用DP算法直接规划出最优SOC轨迹，那么在整个行程中均以此最优SOC轨迹为参考，交通状况发生较大改变时也无法实时改变。为了增强SOC参考轨迹的实时性，这里使用DP算法根据实时交通信息对预测时域内的SOC轨迹进行规划，当时间向前滚动时，再次使用DP算法对预测时域内的SOC轨迹进行规划，直至到达目标点。

众所周知，DP算法应用于SOC轨迹规划存在两个限制条件：（1）必须获得预测时域内的全程信息；（2）DP算法计算量巨大，无法实现实时控制。对于第一个问题，使用智能交通系统已经解决；对于第二个问题，由于预测时域内信息量较小，使用DP算法进行SOC轨迹规划时计算量相对较小，其次，预测时域内的SOC参考轨迹规划问题，可以预留两到三个计算周期，也就是为预测时域内的SOC轨迹规划问题留足充裕的计算时间。

预测时域内车辆加速度、速度、转矩需求预测由式（5）计算得到，动态规划的目标函数为式（7）给出的成本函数最小化，约束条件为式（10）给出的约束。动态规划的计算包括逆向求解和正向计算两个步骤，具体操作可参考文献［10］，这里不再赘述。

5 实验分析与验证

以4.1节中重庆大学至长安福特间的路线为实验对象，途经杨公桥、内环快速、机场路等，整个行程长26.3km，全程耗时2896s。从交通环境和车辆仪表中提取实验车辆的行驶工况，工况速度和加速度随时间的分布情况，如图6所示。

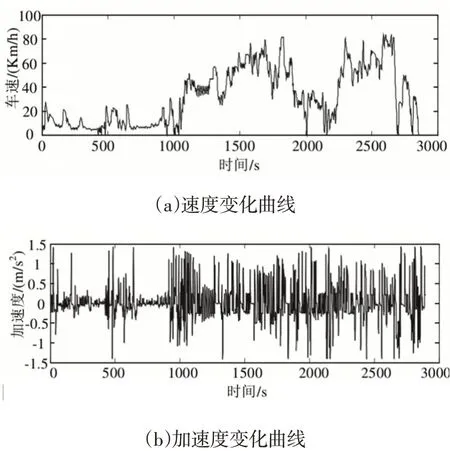
图6 实际工况Fig.6 Actual Driving Cycle

使用支持向量机对行驶工况进行识别并自适应调整衰减因子Td，使用工况自适应指数预测模型对车辆状态进行预测，结果如图7所示。

图7 自适应指数模型预测结果Fig.7 Adaptive Exponential Model Prediction Result

由图7可以看出，车速变化缓慢时，衰减因子Td较小，，车辆处于平稳驾驶状态；当车速急剧变化时，衰减因子Td较大，车辆处于激进驾驶状态，因此衰减因子能够随车辆状态的变化自适应调整。预测车速与实际走势一致，且预测车速能够紧贴实际车速，体现了很高的预测精度。

为了形成对比，这里使用三种方法规划SOC参考轨迹，分别为：（1）根据PHEV的实际工况，使用全局DP算法SOC轨迹，此轨迹为理论最优，为其他控制方法提供参考；（2）根据智能交通系统获取的实时交通信息，使用DP算法规划预测时域内SOC轨迹；（3）无法获取实时交通信息，只已知全程路程或全程耗时，此时使用线形均匀消耗为最优。设定SOC初值为0.5，到达目标点时SOC值设定为0.3，则使用三种算法规划的轨迹如图8所示。

图8 不同算法规划的SOC轨迹Fig.8 SOC Trajectory Planned by Different Algorithm

由图8可以看出，全局驾驶工况已知时全局DP算法规划的SOC曲线，与基于实时交通信息规划的SOC曲线走势非常相似，说明基于实时交通信息的SOC轨迹规划有效。使用带SOC参考轨迹的自适应指数模型预测控制对混合动力汽车进行控制，不同SOC轨迹控制的工作点及统计情况，如图9所示。

分析图9（a）并对比图9（b）（c）（d）可知，基于全局DP算法的控制方法由于将车辆行驶工况作为已知条件，因此具有最高的工作效率，发动机工作点集中在低燃油消耗率点处；基于实时交通信息的控制方法也具有较高的工作效率，发动机主要工作在低燃油消耗率点处，略差于全局DP算法得到的理论最优控制方法，但是大大优于无交通信息参考的控制方法，说明这里提出的基于交通信息的指数模型预测控制具有极高的控制效率，可以实现经济性控制。统计三种方法的SOC初始值、最终值、使用成本，结果如表2所示。

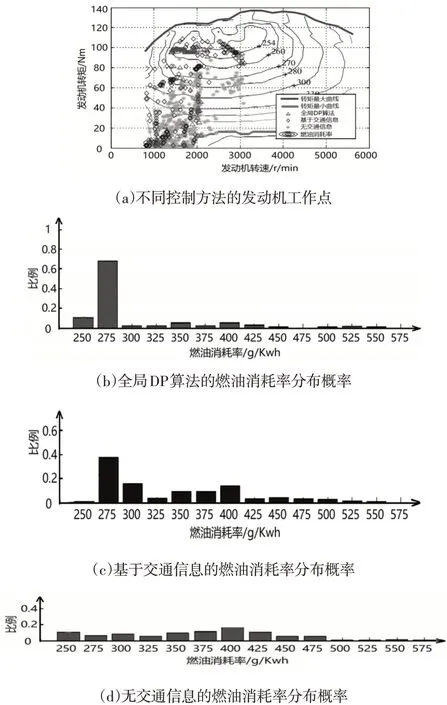
图9 发动机燃油消耗率分布概率Fig.9 Engine Fuel Consumption Rate Distribution Probability

表2 控制结果Tab.2 Control Result

由表2可知，在SOC终值设定为0.3的情况下，三种控制方法最终的SOC值误差均不大，将全局DP算法实现的最优控制经济性定义为100%，则这里提出的基于交通信息的自适应指数模型预测控制可以实现96.22%的经济性，具有极高的使用经济性，而无交通信息参考只能实现84.34%的经济性。这是因为使用智能交通系统实时获取交通信息，根据实时交通信息规划SOC参考轨迹具有很强的时效性，且能够根据交通工况调整转矩分配比例，实现最优的使用经济性。