电液伺服阀测试台的开发

2021-10-20余晨阳陈新元彭海洋桂晓江

机械设计与制造 2021年10期

余晨阳，陈新元，彭海洋，桂晓江

（1.武汉科技大学机械学院，湖北武汉430081；2.广东省韶关市质量计量监督检测所，广东韶关512000；3.江苏力源液压机械有限公司，江苏淮安223001）

1 引言

电液伺服控制在控制领域中起着十分重要的作用，性能的好坏直接影响着控制系统质量［1］。伺服阀其本身结构精密，价格昂贵。因此在伺服阀的使用前和使用过程中，应进行各项的性能测试，包括空载流量测试、压力增益测试、内泄漏测试等，通过测试了解其性能和指导维修。

综合上述考虑，提出并设计了一种能够用于各种伺服阀测试的测试系统，测试过程中通过上位机完成对整个系统的控制，并对采集到的信号进行曲线绘制、信号分析、数据存档、输出报表等工作。

在对采集到的信号分析过程中发现，测试系统会受到各类噪声信号的干扰。因此，针对以上情况采用了不同的滤波器对噪声的剔除效果进行了对比研究，选择效果更佳的迭代滤波器。

2 测试系统的组成

2.1 能源系统

系统主要参数为：最大流量为100L/min，最高工作压力为31.5MPa。在泵的入口采用带有报警装置的蝶阀，增加实验的安全性能。出口配置有压油过滤器保证被测伺服阀产品及各元件工作的可靠性。油箱配备了温度和液位报警系统。供油回路的压力调整通过电磁溢流阀远程控制实现。

2.2 测试试验台

试验台为待测元件、仪表和传感器提供安装平台，为降低使用过程中的故障发生率，采用可靠性较高的无泄漏电磁开关阀实现对不同油路的切换控制。并采用集成油路简化油路结构，减少了外部油路连接。

2.3 测控系统

数据采集处理及电气控制系统由动力电控柜、试验操作控制台、上位机台、软件及人机界面、数字显示屏组成。数据采集控制分别采用美国NI公司数据采集系统及西门子型号为S7-200的PLC，系统组成，如图1所示。

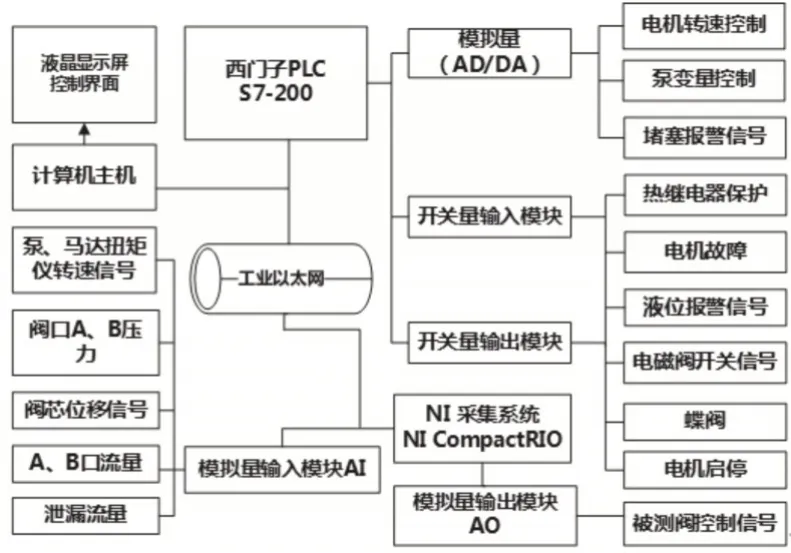
图1 测控系统Fig.1 Measurement and Control System

2.3.1 PLC控制系统

运用电控柜引入试验台总电源，用于对液压动力系统的各电动机供电并控制起停运行或变频调速。采用PLC向工控机提供电动机运行状态信号。向油源系统、试验台操作控制台、工控机柜和其他用电点提供所需的电源，采集控制柜放置在封闭式台架中。油路系统中的各个阀的报警信号、油箱液位信号、温度报警信号、油路切换信号、油路的控制信号主要靠PLC来处理完成，以此保证设备的可靠性及稳定性。

2.3.2 CAT系统

CAT系统采用NI公司的LABVIEW开发，其图形化的编程和丰富的通讯方式，使得其拥有其它编程语言无法比拟的可读性和交互性，可以快速的组建自己的虚拟仪器系统［2］以满足测试系统的需求，缩短软件的开发周期。流程图如图2所示，该测试程序能完成压力、流量等参数的自动采集，根据测试项目的不同进行数据处理、存储备份，并由计算机自动生成相应的试验曲线及试验报告，并根据需要予以保存和打印输出，试验数据以XLS格式保存，以此保证和其他软件的兼容性，便于后期对数据进行其他的分析和处理。

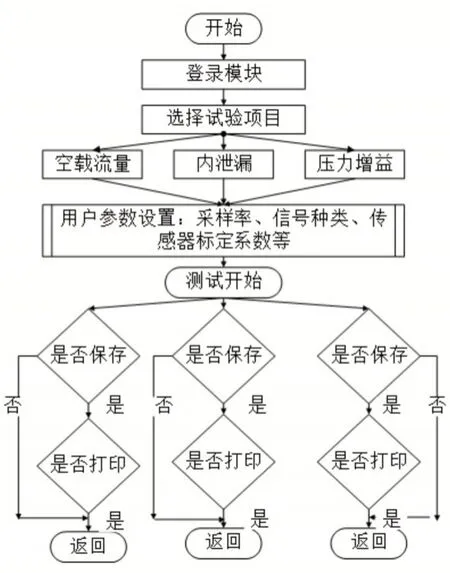
图2 软件流程图Fig.2 Software Flow Chart

在进行各项测试前应该对测试系统进行参数设置，以满足不同的测试项目的需求。以空载流量特性测试为例，测试系统应对模拟输入、模拟输出，采样时钟的采样率和采样点数、输出信号的类型进行设置，软件参数设置界面，如图3所示。

图3 测试系统参数设置界面Fig.3 Testing System Parameter Setting Interface

在如图4信号输出模块中，为增加测试精度，在信号开始和结束阶段，分别加入一段归零信号，对信号进行校正，保证阀芯的初始位置和结束位子均为中位。其中，采样点数，波形采样率，波形个数，信号周期的关系如下：

图4 信号发射模块Fig.4 Signal Transmitting Module

式中：N-总的模拟输出采样点数；n-信号波形个数；FS-波形采样率；T-信号周期；N0-归零信号点数。

3 电液伺服阀静态测试原理

3.1 空载流量特性测试

测试系统液压原理图如图5所示，当伺服阀处于空载工作状态即A、B口之间没有负载的情况下，模拟输入电压信号和采集到的流量信号之间对应的关系曲线就是空载流量特性曲线［3］。

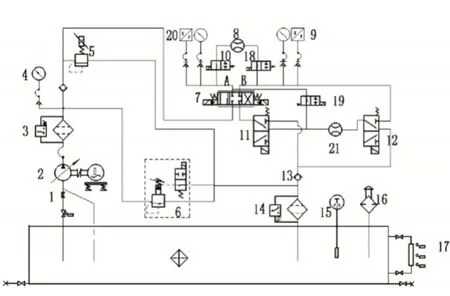
图5 液压系统原理图Fig.5 Schematic Diagram of Hydraulic System

具体测试方法如下：（1）通过工控机使电磁截止阀10，18得电开启，电磁三通换向阀11得电开启，电磁截止阀19失电关闭。（2）设定电磁溢流阀6在该试验系统中所需的溢流压力，启动油泵。（3）通过测试软件模拟输出模块输出一个幅值为±V完整的三角波信号。（4）采集模拟输出信号和流量传感器8的流量信号，生成空载流量特性曲线。

3.2 压力增益特性测试

压力增益特性是在阀的额定供油压力下，关闭A、B之间回路。同时通过压力传感器来分别检测A、B两个油口的压力PA和PB，得到的对应的压力信号和模拟输入电压信号的关系曲线［9］。

具体实验方法如下：（1）通过工控机使电磁截止阀10，18失电关闭，电磁三通换向阀11得电开启，电磁截止阀19失电关闭。（2）设定电磁溢流阀6在该试验系统中所需的溢流压力，启动油泵。（3）通过测试软件模拟输出模块输出一个幅值为±V完整的三角波信号。（4）通过采集卡采集模拟输出信号和A、B口压力信号，生成压力增益特性曲线。

3.3 内泄漏特性测试

内泄漏特性是指在额定供油压力下，关闭A、B之间的口供油回路，模拟输入电压信号和采集到的回油口的流量信号之间对应的关系曲线。

具体实验方法如下：（1）通过工控机使电磁截止阀10，18，19失电关闭，电磁三通换向阀11，，12失电处于常位。（2）设定电磁溢流阀6在该试验系统中所需的溢流压力，启动油泵。（3）通过测试软件输出一个正负值均为测试阀额定信号大小的线性信号。（4）采集输出信号和流量计21的信号，生成内泄漏特性曲线。

4 测试系统中的滤波研究

由于液压系统处于较为复杂的工作环境中，其中机械振动、电气干扰、液压介质温度特性均会对系统的正常信号造成一定程度的干扰，对特征曲线的绘制带来很大的影响［4］。所以测试系统需要对采集到的数据进行滤波处理。目前液压系统中大多采用数字滤波器对原始信号进行处理，以此初步滤除和正常信号频段相差较大的干扰信号。但因为数字滤波器对不同频段的信号没有自适应的能力所以在处理和正常信号频段接近的干扰时效果不佳，并存在一定程度的峰值衰减［5］。

为了准确过滤这些干扰信号，采用迭代滤波分解算法，对信号进行处理。该算法使用foker-planck方程构造滤波函数，通过若干次的迭代运算，使各类干扰从原始信号中剥离出来，从而得到具有稳定特征的模态分量，能够有效降噪精确度较高［6］。

4.1 迭代滤波分解原理

迭代滤波分解（iterative filter，decomposition，IFD）能够按照信号频段的不同自适应地将一个复杂信号分解为若干个相互独立的内禀模态分量和一个趋势项之和。该方法包含了用于提取特征分量的内循环和判断截止条件的外循环［7］。

4.1.1 内循环过程

内循环过程中，通过计算待分解信号z(t)与滤波函数ω(t)的卷积得到滑动算子Γ(z(t))：

式中：l(z)-滤波区间，可利用式（2）得到：

式中：λ-设置参数1.6～2；m-分解信号的极值点数；N-信号长度。

将（2）式中计算得出的滑动算子从信号z(t)中提取出来后得到了波动算子k(z(t))：

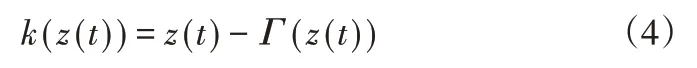
若波动算子k(z(t))满足IMF条件，则k(z(t))为提取到的IMF分量，但初次计算的结果不能得到固定频率的IMF分量，需要进行反复的筛选，重复（2）至（5）过程：

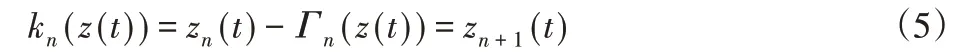
当n趋近于无穷大时，若I(t)满足IMF条件，则完成一次IMF分量提取。

在实际计算中式（6）中的方法由于计算时间的限制通常采用基于泰勒级数等价后的公式（7）作为第i个波动算子的IMF判据。

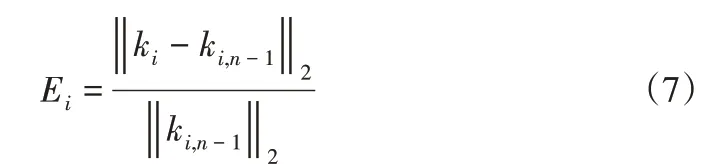
4.1.2 外循环过程

外循环的作用在于停止内循环对IMF的提取进程并从分解信号z(t)中移除内部循环中识别的IMF分量I(t)，以计算剩余分量：

当呈现明显的趋势特征时，迭代终止，并且完成整个迭代滤波器分解过程，否则r(t)赋值为重复内循环过程。

4.2 实际滤波效果

对空载流量特性曲线、压力增益特性曲线、内泄漏特性曲线分别采用巴特沃斯［8］数字滤波器（低通滤波器，通带为（0～10）Hz）和迭代滤波分解对原始信号进行处理。

4.2.1 空载流量信号处理

空载流量原始信号，如图6所示。存在明显的噪声干扰，这些干扰信号会对空载流量曲线滞环的判断、流量增益的计算等造成很大的干扰、影响特征曲线的分析。

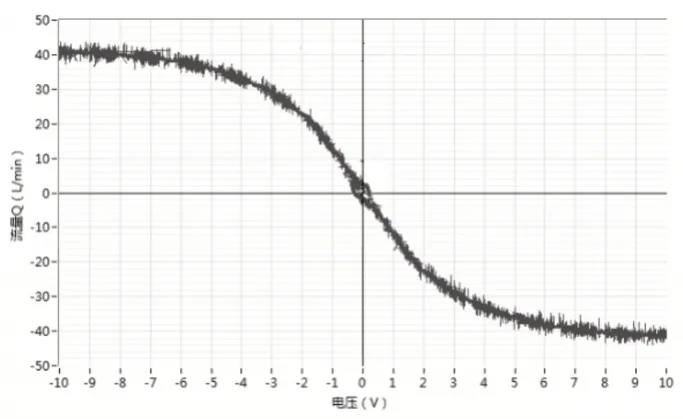
图6 空载流量原始信号曲线Fig.6 No-Load Flow Original Signal

首先，采用巴特沃斯数字滤波器进行滤波效果图，如图7所示，经过数字滤波器对原信号进行处理后信号的毛刺情况有所改善但是对信号的处理效果还是不够理想，例如：在控制流量为零时的电压信号的毛刺对滞环的判断还是带来了一定程度的影响。

图7 数字滤波器滤波后空载流量曲线Fig.7 No-Load Flow Curve after Digital Filter Filtering

针对数字滤波器对信号处理后效果不够理想的情况，通过采用迭代滤波算法对信号进行分解，对含有干扰的原始信号进行滤波处理。经过五次迭代提取IMF分量后，结果图如图8所示。

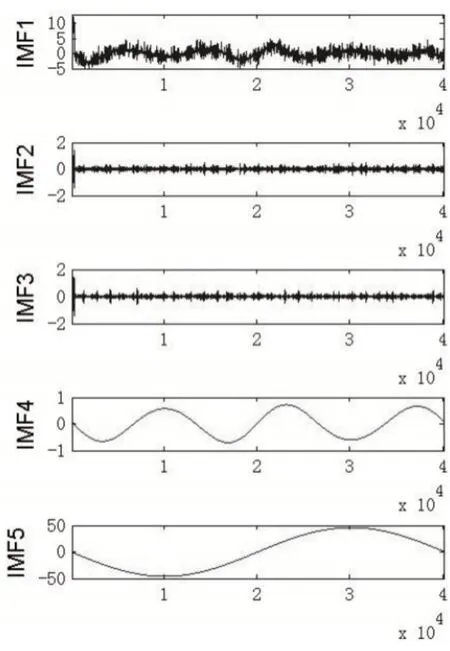
图8 迭代滤波IMF分量图Fig.8 Iterative Filtering IMF Component Diagram

从图8（迭代滤波IMF分量图）中可以看出噪声信号集中在IMF1到IMF3分量中且存在频段和正常信号接近的谐波干扰IMF4。因此在分解时只要去掉这些干扰信号，就可以达到较好的过滤效果，滤波后的信号为：

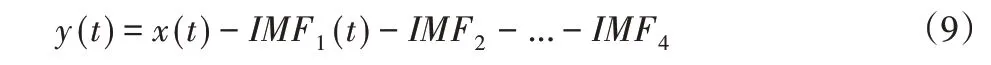
去除干扰信号后的空载流量特性曲线如图9所示，经迭代滤波后整段曲线的毛刺明显减少，光滑性也有所增加，提高了数据的准确度。

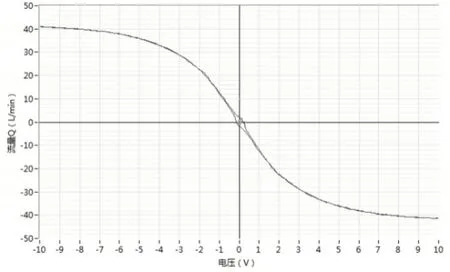
图9 迭代滤波后空载流量曲线Fig.9 No-Load Flow Curve after Iterative Filtering

为进一步验证迭代滤波算法对频段接近信号的剥离效果，分别对图8中的IMF4特征分量和剩余信号分量IMF5分别进行FFT变换，得到的频谱图，如图10所示。由图可以看出频率十分接近的干扰信号也从原始信号中剥离了出来，有效避免了在干扰信号和信号频率接近的情况下普通数字滤波器存在频率混叠的问题。

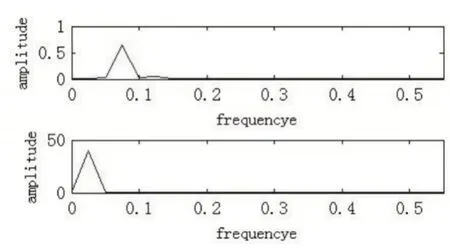
图10 IMF4特征分量和剩余信号IMF5频谱图Fig.10 IMF4 Characteristic Components and IMF5 Spectrum of Residual Signals

4.2.2 压力增益曲线滤波处理

考虑到设备老化和其他因素的影响压力变送器的干扰情况严重，压力增益曲线原始信号，如图11所示。分别采用巴特沃斯数字滤波器和迭代滤波算法所构造的滤波器，分别对原始信号进行处理，处理后的效果图，如图12、13所示。

通过图12、13的对比可知在噪声干扰非常严重的情况下，数字滤波能起到一定程度的降噪和平滑曲线的效果，但是滤波效果没有迭代滤波理想。

图12 数字滤波器滤波后压力增益曲线Fig.12 Pressure Gain Curve of Digital Filter after Filtering

图13 迭代滤波后压力增益曲线Fig.13 Pressure Gain Curve After Iterative Filtering

4.2.3内泄漏特性曲线滤波处理

内泄漏特性测试中，系统同样受到一定程度的干扰，内泄漏曲线原始信号，如图14所示。分别采用上述数字滤波器和迭代滤波分解方法分别对内泄漏曲线进行处理。效果如图15、16所示。

图14 内泄漏原始信号曲线Fig.14 Internal Leakage Original Signal Curve

图15 数字滤波器滤波后内泄漏曲线Fig.15 Digital Filter Filtered Internal Leakage Curve

4.3 数据标准差对比

为验证数字滤波器和迭代滤波算法的准确性，分别对巴特沃斯数字滤波和迭代滤波处理后的数据进行标准差的计算，如表1所示。通过五组数据标准差的对比可以看出迭代滤波器的标准差均小于数字滤波器，数据的精确度更高。

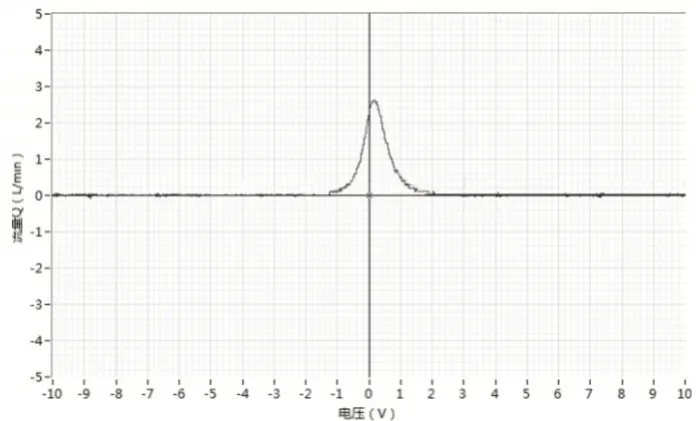
图16 迭代滤波后内泄漏曲线Fig.16 Iterative Filtered Internal Leakage Curve

表1 数字滤波和迭代滤波后和原信号的标准差Tab.1 Standard Deviation of Original Signal After Digital Filtering And Iterative Filtering

通过上述曲线的对比以及数据标准差的对比，结果表明，迭代滤波器的滤波效果优于巴特沃思数字滤波器。在噪声干扰严重的情况下，迭代滤波器滤波后平滑性强于巴特沃斯数字滤波器，由于迭代滤波器对不同频率有自适应的特点，在干扰信号频率和信号的频率接近时，迭代滤波器也可以有效的将干扰信号剥离开来，避免了频段相近的干扰信号的混叠，提高了数据的精确性。