混凝土冲击载荷作用下泵车臂架动态特性分析

陈 泽，郭 岗，，吴 亮，田相玉，

（1.中联重科股份有限公司 泵送事业部研发中心，湖南 长沙410205；2.国家混凝土机械工程技术研究中心 技术研究院，湖南 长沙410205）

1 前言

伴随混凝土泵车长臂架、轻量化、大排量、高可靠性、高平稳性的发展趋势，臂架作为混凝土泵车承担混凝土连续输送的核心部件，混凝土流动对臂架动态载荷作用环境越来越复杂，混凝土泵车臂架的振动严重影响到施工质量、效率和安全，提升臂架系统动力品质亟待深入研究。混凝土泵车在实际泵送作业中，臂架系统可简化为一个柔性连续体，混凝土泵送过程中在输送管中产生的周期性冲击压力，使臂架在作业时产生周期性的强烈振动，泵车工作的稳定性因此受到影响，使得臂架末端输送混凝土的软管形成较大振幅，浇筑精度降低［1］。混凝土泵车臂架振动主要由附加混凝土泵油缸周期性推动力的混凝土在输送管内的周期性流动冲击载荷所引起［2］。泵车臂架固有频率与混凝土在输送管内的周期性流动冲击载荷频率接近可能会引起共振［3］。为了避免共振现象产生，在保证泵车作业的高可靠与高效率下，改善泵车臂架的振动性能，就要从泵送频率或泵送固有频率入手了解臂架的动态特性［4］。为此，以某型号长臂架泵车为研究对象，建立臂架柔性多体有限元模型，对臂架进行模态分析与动态响应分析，了解臂架的动态特性，通过动态应力、模态及加速度响应测试并进行验证，以保证模型的有效性，为臂架系统的减振、疲劳及动态设计提供理论依据。

2 混凝土流动冲击载荷数学模型

由于泵送混凝土油缸反复的循环作业，油缸液压冲击增加了臂架结构的动应力［5］。特别是输送管混凝土的摩擦力和弯管处混凝土流向改变产生的附加力以及臂架系统末端出料口处的冲击力，使得混凝土泵车臂架系统在输送混凝土至浇筑位置过程中产生强烈振动［6］。混凝土流动冲击载荷主要指泵车工作中由于间歇性混凝土在输送管流动中所产生的作用在泵车臂架上的动态载荷，该载荷是造成臂架振动的主要激励源，工况不同则其间隔时间、幅值大小也不同。混凝土流动冲击载荷主要由混凝土与输送管间的摩擦力、混凝土流向改变时的附加作用力、混凝土平移流动时的作用力组成，混凝土与输送管间的摩擦力是指间歇性混凝土在输送管中流动时对管壁产生的作用力，又由于混凝土是周期性流动的，因此这种作用力也是周期性的。周期性载荷作用于臂架上将会引起臂架振动，其中最主要的一种载荷即为摩擦力。混凝土流向改变时的附加作用力是指由于惯性效应，当混凝土在输送管中流动中受力改变流向时，混凝土将对管壁施加附加作用力。混凝土平移流动时的作用力是指混凝土在流经部分弯头处时，为便于臂架折叠，输送管的布置会使混凝土的流线发生平移。现以整个臂架系统为研究对象，前述所有载荷作用在臂架系统上，定义混凝土流速最大时作用于臂架上的空间力系为广义力F*，该力即为前述计算得到的混凝土流速最大时混凝土与输送管间的摩擦力系f、混凝土流动方向改变时产生的附加作用力系F和混凝土平移流动时引起的力偶系M之总和。

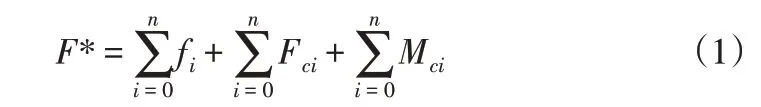
由于混凝土流速是随时间周期性变化的，因此该力系大小也是随时间周期变化的。由前述（1）式，混凝土的流速可以用周期性变化的函数P(t)来表征：

定义作用于臂架系统上的随时间周期性变化的空间力系F*(t)，如图1所示，F*(t)同样可以用周期性变化的函数P(t)来表征：

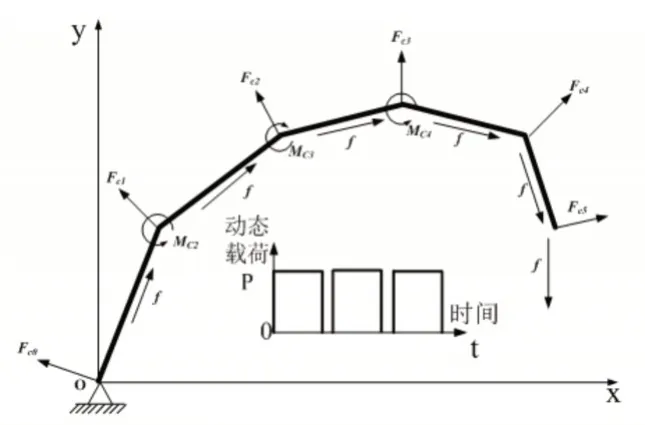
图1 作用在臂架上的周期性变化的广义力F*(t)Fig.1 Periodically Varying Generalized Forces Acting on Booms

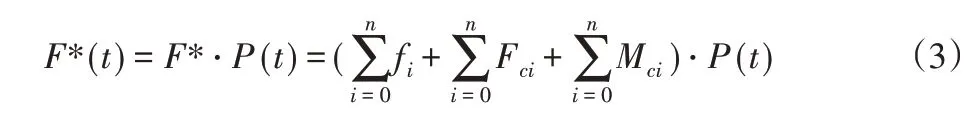
其中，

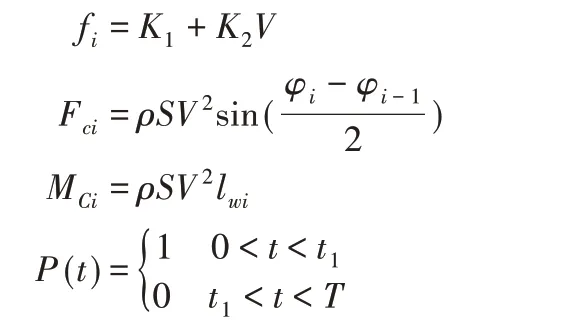
式中：f-柱塞流对于管道单位面积上的摩擦力（Pa）；K1-粘着系数（Pa）；K2-速度系数（Pa/(m·s-1)）；V-混凝土的流速（m s）；S-输送管截面积（m2）；lwi-Z形弯头处的流线平移量（m）。

臂架水平姿态是混凝土泵车作业最典型的工况，由于在水平姿态下臂架系统的振动尤为强烈，同时与建立的仿真模型姿态保持较好的一致性，便于仿真模型的比较和验证［7］。因此选择水平姿态工况作为研究对象，水平姿态典型臂架姿态下的总体载荷即，如图2所示。

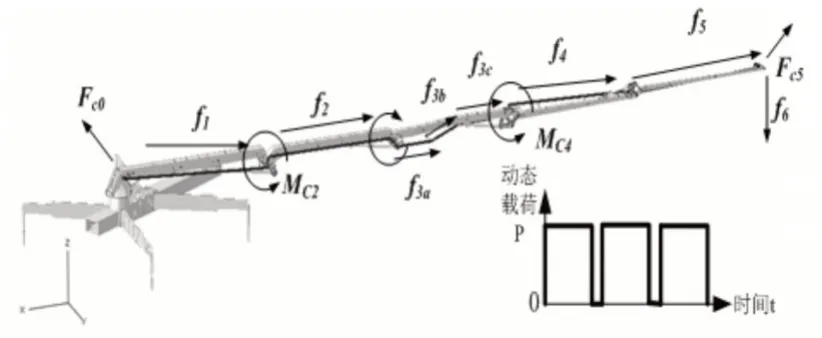
图2 水平姿态下作用在臂架上的周期性变化的广义力F*(t)Fig.2 Periodically Varying Generalized Forces Acting on the Boom in Horizontal Posture

3 结构建模与仿真分析

3.1 臂架系统有限元建模

结合柔性多体动力学建模思想和有限元方法，建立基于柔性多体有限元的混凝土泵车臂架模型，得到了完全的、高质量的四边形网格模型，并且能准确地反映出臂架结构复杂的形态特征，最终的臂架系统结构的有限元模型共包含215627个单元。泵车臂架选用的材料高强度钢主要为WELDOX700E和WELDOX900E，其弹性模量E=206×106MPa。有限元计算阶段选用线弹性模型，泊松比μ取0.3。如图3所示，为水平姿态泵车臂架模型，在转台位置施加了固定约束边界条件。

图3 水平姿态泵车臂架模型边界条件示意图Fig.3 Schematic Diagram of Boundary Conditions for the Horizontal Attitude Pump Truck Boom Model

3.2 动态特性分析

采用ABAQUS频率提取分析步对水平姿态下的泵车臂架模型进行模态分析。混凝土泵车在泵送作业中输送管内充满混凝土，模态分析时需要考虑混凝土的重量，因此在有限元模型中将混凝土的重量以等效密度的形式加到输送管上，臂架末端软管及其中混凝土的重量以质量点的形式附加在输送管末端对应节点上。水平姿态臂架模型的模态计算结构前四阶固有频率其对应振型，如图4所示。

图4 水平姿态臂架前四阶振型Fig.4 Front Fourth-order Vibration Modes of the Horizontal Attitude Boom

3.3 动态响应分析

模型单元规模大，并且需要计算结构在100s时间量级上的动态响应，故采用模态叠加法应用结构的固有频率和振型来进行臂架结构的动态响应分析。考虑到臂架动态响应主要受低阶模态控制，应用模态叠加法时只截取系统前20阶模态。为提供足够的振动衰减时间，动态响应计算时长取125s。根据臂架系统模态试验数据，臂架动态仿真模型的结构阻尼取1.5%。泵车臂架动态响应计算的边界条件与模态计算时相同，在四个支腿底部施加铰支约束。

通过水平工况下臂架系统的稳态响应计算，臂架末端位移响应结果，如图5所示臂架末端Z向位移曲线，振幅大小为343mm，臂架末端加速度响应结果，如图6所示臂架末端法向加速度曲线，波峰位置加速度大小为0.59g，波谷位置加速度大小为0.48g。动态应力响应结果为图7测点沿臂节轴线方向应力峰值计算结果，最大拉应力发生在六号测点，大小为397.9MPa；最大压应力发生在十三号测点，大小为390.6MPa。

图6 末端法向加速度曲线Fig.6 Terminal Normal Acceleration Curve

图7 点计算应力峰值Fig.7 Points to Calculate the Stress Peak

4 试验验证

为验证臂架系统动态特性的数学模型的有效性，选某型号长臂架泵车进行了水平工况下臂架系统的动态响应试验以及模态试验。试验中臂架系统的五节臂上总共布置了32个动态应变测点，26个加速度传感器以及5个倾角传感器；应变测试系统采用江苏东华DH5922动态应变仪进行动应变的数据采集，动态应变仪同时记录倾角传感器数据来监控臂架姿态变换，臂架加速度响应由LMS数采系统完成数据采集，动态应力、模态及加速度响应测试，如图8所示。

图8 动态应力、模态及加速度响应测试Fig.8 Dynamic Stress，Modal and Acceleration Response Test

在进行混凝土泵送激励下动态应力试验的同时，开展了臂架系统的工作模态测试，在进行混凝土泵送激励下动态应力试验的同时，通过布置在臂架末端的三向加速度传感器，记录臂架末端在水平工况下的加速度变化情况，水平姿态下臂架末端垂向加速度响应曲线，如图9所示。模态计算值、试验值及误差，如表1所示，危险部位动应力幅值计算值、试验值及误差，如表2所示，臂架末端振幅、臂架末端加速度幅值计算值、试验值及误差，如表3所示。

图9 臂架末端加速度响应曲Fig.9 Acceleration Response Curve of the Boom

表1 模态计算值、试验值及误差Tab.1 Modal Calculation Values，Test Values and Errors

表2 危险部位动应力幅值计算值、试验值及误差Tab.2 Calculated Value，Test Value and Error of Dynamic Stress Amplitude of Dangerous Parts

表3 臂架末端振幅计算值、试验值及误差Tab.3 Calculated Value，Test Value and Error of Arm End Amplitude

表4 臂架末端加速度幅值计算值、试验值及误差Tab.4 Calculation Value，Test Value and Error of the Acceleration Amplitude at the End of the Boom

对泵车臂架系统的动态响应仿真结果进行了误差计算和相关性分析，模态计算结果与试验值的比较，误差均值为5.7%，危险部位动应力幅值计算值与试验值的比较，误差均值为24.96%，臂架末端振幅计算值与试验值的比较，误差值为19.3%，臂架末端加速度幅值计算值与试验值的比较，误差值为15.7%，满足技术指标考核要求，结果表明动态响应仿真结果与试验数据有较好的一致性。

5 结论

通过混凝土在输送管中的流动特性及分项载荷的理论分析，建立了基于流速周期性变化表征函数的混凝土流动冲击载荷的近似数学模型，依据计算机试验辅助建模方法和动态试验数据，构建了能够准确反映臂架系统动态特性的模型，进行了模态分析与动态响应分析，再通过动态应力、模态及加速度响应测试等实车动态试验对研究成果进行验证。以水平工况下动应力、位移和加速度的实车测试数据为依据，对泵车臂架系统的动态响应仿真结果进行了误差计算和相关性分析，模态计算结果与试验值的误差均值为5.7%，危险部位动应力幅值计算值与试验值的误差均值为24.96%，臂架末端振幅计算值与试验值的误差值为19.3%，臂架末端加速度幅值计算值与试验值的误差值为15.7%，初步形成臂架系统可靠、高效的有限元仿真分析方法，为臂架系统的减振设计、抗疲劳设计及结构动态设计奠定了基础。