张量奇异谱分解与极限学习机的故障诊断方法

2021-10-20沈宝国谢中敏

机械设计与制造 2021年10期

胡超，沈宝国，杨妍，谢中敏

（江苏航空职业技术学院航空工程学院，江苏镇江212134）

1 引言

旋转机械中，滚动轴承是运用最为广泛同时也是损坏率最高的部件之一。在以往的故障诊断中，通常采用油液分析法进行故障部件识别［1］。但由于油液分析存在人为因素干扰，导致其应用受到限制。随着转子动力学的深入研究，诸多学者采用提取振动信号的故障频率进行诊断，如：快速傅里叶变换［2］、小波分析［3］、经验模态分解［4］等。但这些方法均存在部分缺陷，如：快速傅里叶属于整体变换，利用全部时域信号，不适宜于处理故障信号等非性问题；小波分析受制于窗口函数选择；经验模态分解容易产生模态混叠现象。

近年来，奇异谱分析能够有效地将时间序列中信号和噪声剥离［5］，因此被用于轴承故障诊断中。但奇异谱在构造时，由于子矩阵选择的不同，导致重构信号差异较为明显。考虑到高维信号中包含着部分有用信息，因此张量分解被运用到奇异谱分析中［6］。由于张量分析能够有效的将信息从一维映射到高维中，能够通过标准张量分解将纯谱信号从高维中还原。因此，张量奇异谱被运用到机械故障诊断［6］、轴承故障诊断［7］、发动机故障诊断［8］中。

虽然张量奇异谱能够很好的对信号进行分离，但频谱分析时如果方法不当亦会导致倍频混杂难以快速找到。因此，近来诸多故障诊断采用信号处理和人工智能结合的方法，如：支持向量［9-11］、人工神经网络［12，13］、Elman［14］和RBF网络［15］对轴承故障进行有效地诊断。诸如BP这些部分前馈神经网络易陷于局部极值等问题，导致在故障诊断中效果较差，因此文献［16］提出极限学习避免传统网络对学习速率、终止条件、易陷于局部极优等缺陷，因而得到广泛运用，如：皮骏［17］等用改进遗传算法优化极限学习机并用于轴承故障诊断中。为了更好实现滚动轴承故障诊断，结合张量奇异谱和极限学习机对滚动轴承故障样本实施诊断。

2 张量奇异谱分析

张量奇异谱分析（Tensor singular spectrum analysis，TSSA）是一种能够将数据从低维映射到高维并挖掘信号高维特征的一种方式［18］。其主要思想是：先将一维时间序列利用不重叠的时间窗口将其转换为一个矩阵；其次，使用相空间重构将每行矩阵表示为一个重构的吸引子矩阵，吸引子矩阵形成对应的张量切片，从而得到一个分解的三维张量［19］；最后，使用标准张量分解法将纯谱从高维数据中进行还原。TSSA主要包括时域信号数据的嵌入和分解重构两部分。

2.1 嵌入

假设长度为n的一维时间序列x（t），t=1，2，...，n，被嵌入一个长度为l的不重叠时间窗口中形成矩阵T如式（1）所示。

张量X能够矩阵T得到，将矩阵T视为一个张量多维矩阵，而T的每一行表示张量切片所形成的一个吸引子矩阵。在此分割过程中，在同一个方向执行，其示意图如图1所示。

图1 中，张量X的切片Xi：：是由矩阵T的第i行经过相空间变换重构得到的。设J表示重构窗口长度、K表示重构嵌入维度、τ表示延迟时间、I表示矩阵T的维度I=n/l，则l=（K-1）×τ+J，张量X的切片Xi：：中Xijk可由式（2）计算的得到：

图1 张量X的切片构造过程Fig.1 The Construction Process of the Slices of Tensor X

式中：i=1，2，...，I；j=1，2，...，J；k=1，2，...，K。则张量X的切片Xi：：可表示为式（3）：

2.2 分解重构

对获得的I×J×K维张量X进行CANDECOMP/PARAFAC张量分解［7］，将其分解为分秩为1的张量和，CANDECOMP/PARAFAC张量分解与张量分解相似［20］，其分解模型可表示为式（4）所示［21，22］，其示意图如图2所示。

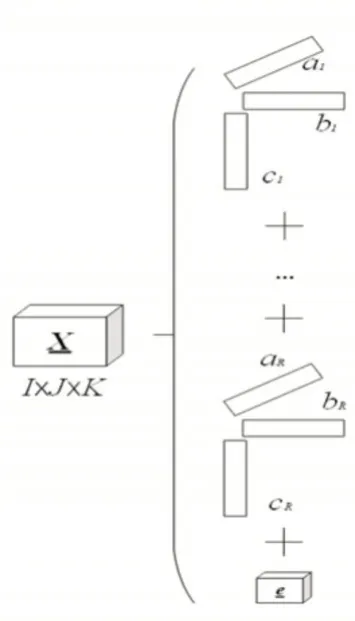
图2 CANDECOMP/PARAFAC张量分解示意图Fig.2 The Illustration of CANDECOMP/PARAFAC Decompose

式中：R-对应张量X的秩；ar∈RI×1、br∈RJ×1、cr∈RK×1分别为矢量因子矩阵A∈RI×R、B∈RJ×R、C∈RK×R的元素；e-∈RI×J×R表示残差项。则式（4）可表示为式（5）。

TSSA算法采用最小二乘法求解A、B、C因子矩阵，定义重构信号和原信号的误差函数如式（6）所示。

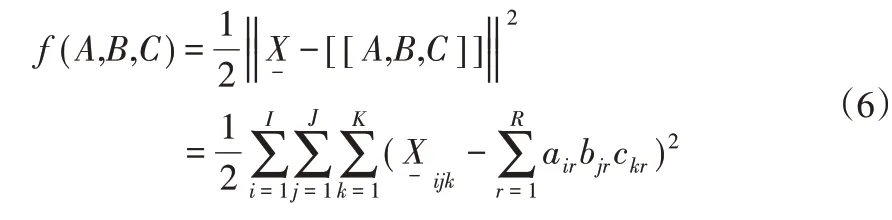
在求解A、B、C因子矩阵时，先改变B和C求A，再改变A和C求B，再改变A和B求C，直到收敛位置。

2.3 TSSA方法验证

为验证TSSA在信号分解中的有效性，将奇异谱分析（SSA）作为对比方法，验证TSSA的性能。为了更好的验证TSSA在轴承故障诊断中的性能，采用文献［23］中的仿真信号，其信号可以表示为式（7）所示。

式中：A0-共振振幅；fm-调制频率；φA、φw和CA-常量；B-衰减系数；T=1/fp，fp-故障特征频率；τi-滑动周期产生的平均值时滞；fn-轴承系统的共振频率；n（t）-噪声信号。对于轴承外环故障、内环故障、滚动体故障仿真时，fm-0、fr、fre，其中fr表示旋转频率、fre表示保持架频率。三种故障特征频率如表1所示，对于三种故障类型仿真参数取值如表2所示。

表1 三种类型的故障特征频率Tab.1 The Fault Character Frequency of Three Common Types

表2 三种故障类型的仿真参数Tab.2 Simulation Parameters of Three Common Types

仿真实验中，TSSA算法中的l取值200、J取值50、I=n/l=2000/200=10、τi=1。此处仿真实验以内环故障为例，主要分析内环故障在噪声下、TSSA和SSA处理的频谱变换是否能反映出故障特征频率。仿真实验中用到的仿真信号及噪声如图3所示，频谱变换方法采用快速傅里叶变换。含噪声信号的频谱图如图4所示，TSSA去噪后的频谱图如图5所示，SSA去噪后的频谱图如图6所示。

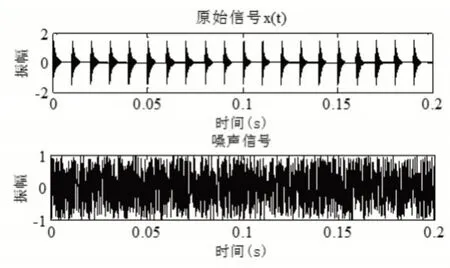
图3 仿真信号Fig.3 Simulation Signal

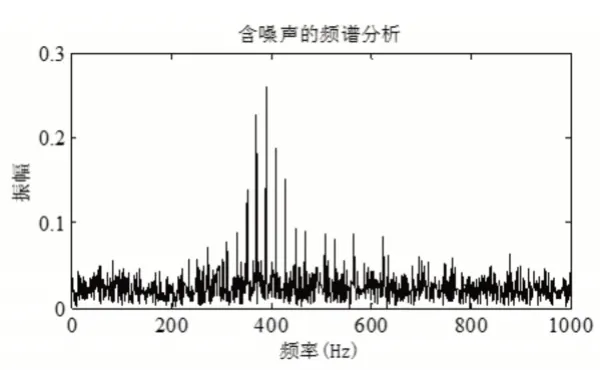
图4 含噪声信号的频域分析Fig.4 Simulation Signal with Noise in Frequency Domain

图5 基于TSSA的频域分析Fig.5 Frequency Domain Analysis with TSSA

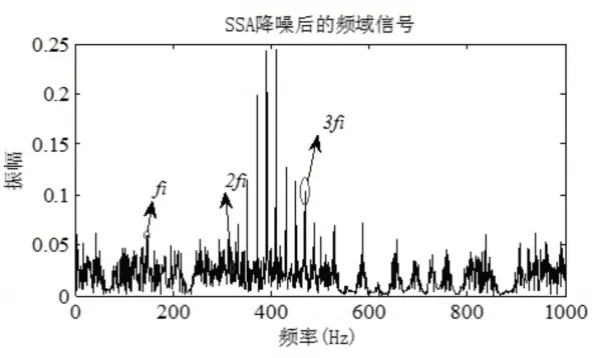
图6 基于SSA的频域分析Fig.6 Frequency Domain Analysis with SSA

从图4到图6的频域图可以看出，含噪声信号的频谱图难以找到内环故障特征频率，而经过TSSA和SSA去噪后的频谱图能够找到对应的倍频；比较图5和图6的频域图，虽然均能在频域图中找到对应的倍频，但是TSSA处理后的信号比SSA效果好些，SSA中的一倍和二倍频难以找到，TSSA相比SSA其一倍频较为明显。但总体而言，经过频谱变换后的信号，虽然能够找到倍频，但由于噪声清洗效果不够明显，导致其倍频寻找难度较大，不利于轴承故障的批量诊断，因此后续轴承诊断过程采用特征参数与极限学习结合的方式进行。

3 极限学习机

文献［16］提出极限学习机（Extreme Learning Machine，ELM）算法，能够克服部分单隐层前馈神经网络的缺陷，且能够逼近任意非线性分段函数［24］。

极限学习机理论在文献［17］中已经详细叙述，此处不再累述，仅简单介绍。ELM网络表示如式（8）所示。

式中：H-ELM网络输出矩阵，其值与输入矩阵、权值、激活函数和阈值有关，具体计算方法参看文献［17］；T′-ELM网络输出矩阵T的转置；β-ELM网络输出权值。输出权值β可由最小二乘求得：

式中：H+-输出矩阵H的Moore-Penrose广义逆。由于最小二乘法能求得唯一解，因此ELM网络使用Moore-Penrose广义逆能够极大的提高学习效率。常用隐含层激活函数如下：

（1）Sigmoid（）函数：

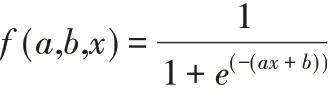
（2）Sin（）函数：

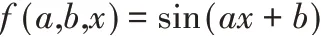
（3）RBF（）函数：

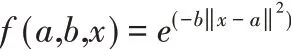
（4）Hardlim（）函数：

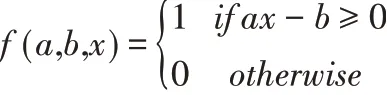
4 TSSA与ELM的轴承故障诊断

4.1 滚动轴承数据来源

所采用的滚动轴承故障振动数据源自美国西储大学的轴承数据中心［25］。轴承故障模拟试验台如图7所示；轴承类型为6205-2RS-JEM-SKF，其基本尺寸参数如表3所示；试验中，电机转动频率1772rpm，采用频率48kHz。

图7 轴承振动分析实验台和采集装置Fig.7 Bearing Vibration Analysis Test Stand and Experimental Instrument

表3 6205-2RS-JEM-SKF型轴承参数Tab.3 6205-2RS-JEM-SKF Type Bearing Parameters

诊断实验中选用的故障类型：内环故障、滚动体故障、外环故障；每类故障样本数据为60组，故障类型标签分别为：1、2、3；三种故障类型的时域波形图如图8所示，图8中仅呈现4000组样本数据点。

图8 三种类的时域波形图Fig.8 Time Domain Waveforms of Three Type

4.2 TSSA降噪处理

对实验室采集到的三类轴承故障振动信号采用张量奇异谱进行分解降噪处理，由于数据量较大，因此此处仅呈现振动信号中某一个整周期的时域波形图。三种故障类型经过TSSA处理后的源振动信号、时域波形图、噪声信号分别如图9～图11所示。

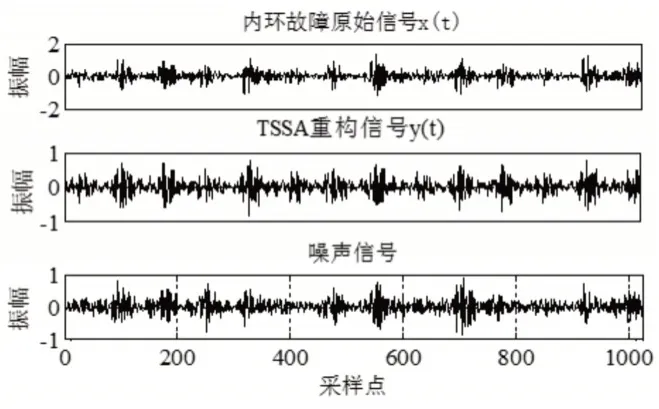
图9 内环故障Fig.9 Fault of Inner Ring

由图9到图11所示，TSSA将部分噪声信号从原始振动信号中剥离，使得有效振动信号变化趋势更为明显，且降噪后的振动信号振动幅值明显减小。在2.3节中的仿真实验表明，对降噪后的时域信号进行频域变换能够实现轴承故障的诊断，但此方法效果不太显著，因此提取时域统计特征参数实施诊断。

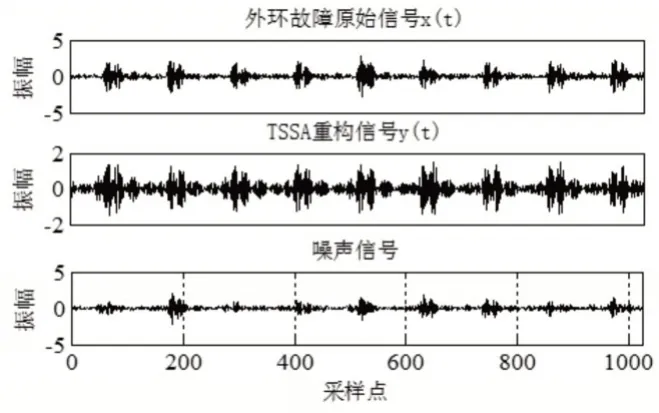
图11 外环故障Fig.11 Fault of Outer Ring

4.3 时域特征参量的提取

根据文献［17］，部分时域特征能够有效反映振动信号的原始特征、减小对信号的扭曲作用，且无需对特征数据进行归一化操作，因此文中提取时域特征参数如下：平均值、峰峰值、均方根值、标准差、偏度、峭度、波峰因子和变异系数。由于每组数据60组，共计180组数据，因此文中数据部分呈现，如表4所示。

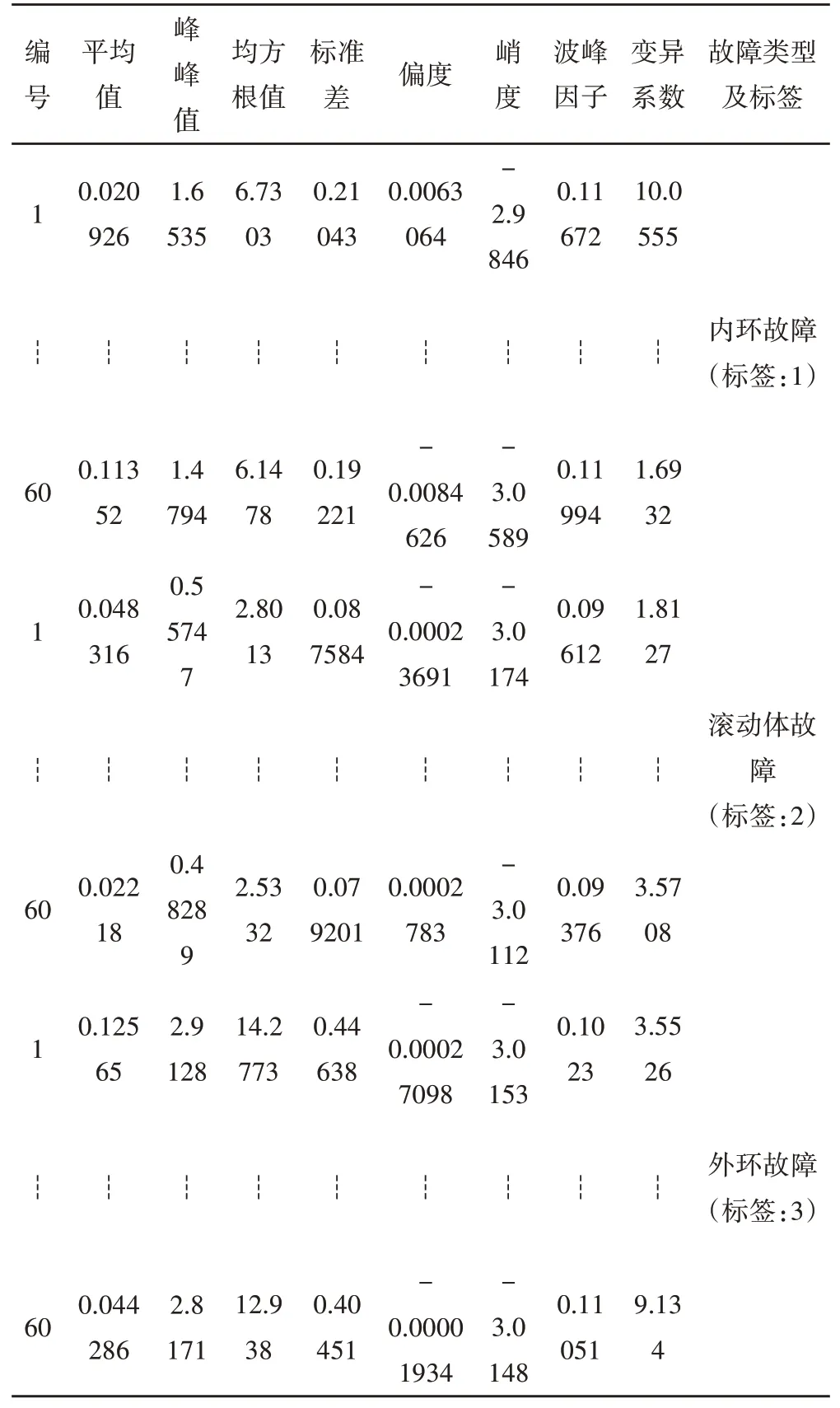
表4 时域特征参量Tab.4 Time-Domain Characteristic Parameters

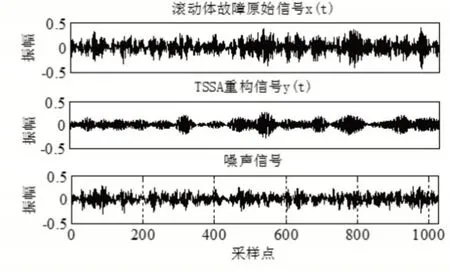
图10 滚动体故障Fig.10 Fault of Ball

4.4 ELM网络设置

极限学习机采用三层网络结构，输入层神经元由输入变量决定，由于时域特征变量8个，因此输入层神经元数量为8；由于隐含层激活函数和神经元数量影响ELM诊断效果，因此隐含层的设置在后续进行讨论选择；输出层为1，直接输出故障类型标签。

5 算法验证

5.1 ELM网络参数的选择

如文献［17］中所述，极限学习机虽然优势较强，但其诊断效果受到隐含层的参数设置。合理选择有效激活函数和神经元数量能够对诊断效果产生积极作用，因此为了后续诊断效果较佳，此处分析激活函数和神经元数量给网络诊断结果带来的影响。Sigmoid（）函数、Sin（）函数、RBF（）函数、Hardlim（）函数随神经元数量变化给诊断结果带的影响，如图12、图13所示。

图12 和图13的诊断结果均在训练集样与测试集样本比例为2：1时的结果，由图可知，ELM网络选择不同神经元时其诊断准确率存在差异。由图12可知，当激活函数选择Sin（）、Sigmoid（）函数时，隐含层神经元数量超过40时，其二者对训练集诊断准确率达到100%；但如图13所示在测试集诊断中，当神经元数量超过60时，二者差异较小，但诊断准确率略有下降；当激活函数采用Sigmoid（）且神经元数量较少时，诊断准确率较高。综上所述，后续滚动轴承故障诊断隐含层激活函数采用Sigmoid（），神经元数量设置在（20～30）之间。

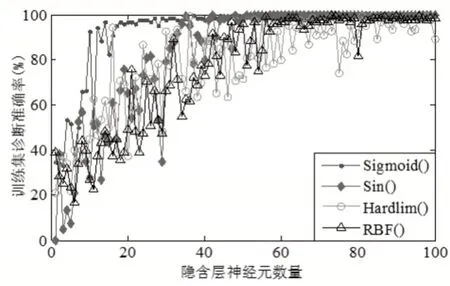
图12 训练集诊断准确率Fig.12 Diagnostic Accuracy of Training Set

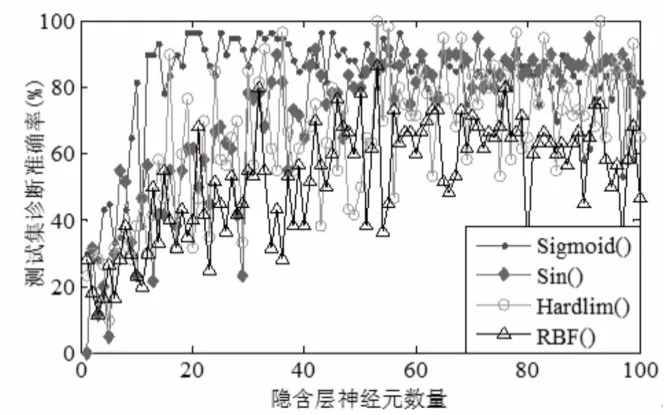
图13 测试集诊断准确率Fig.13 Diagnostic Accuracy of Test Set

5.2 对比算法参数设置

为验证ELM网络在滚动轴承故障诊断中的有效性，将BP、SVM作为对算法。BP神经网络采用三层网络结构，输入层神经元数为8、隐含层为17、输出层为1，即8-17-1的结构；BP中权值、阈值随机产生，隐含层神经元采用S型正切函数tansig，输出层神经元采用S型对数函数logsig，网络训练函数为trainlm。SVM中罚参数和核参数采用随机赋值方式，核函数采用RBF核函数。

5.3 滚动轴承故障诊断结果

使用ELM、SVM、BP网络对滚动轴承故障实施诊断，其中ELM、BP呈现结果均为10次诊断平均值，SVM为重复执行4次中最佳值。诊断测试过程中，样本比例分别为：2：1、1：1、1：2，其诊断结果，如表5所示。

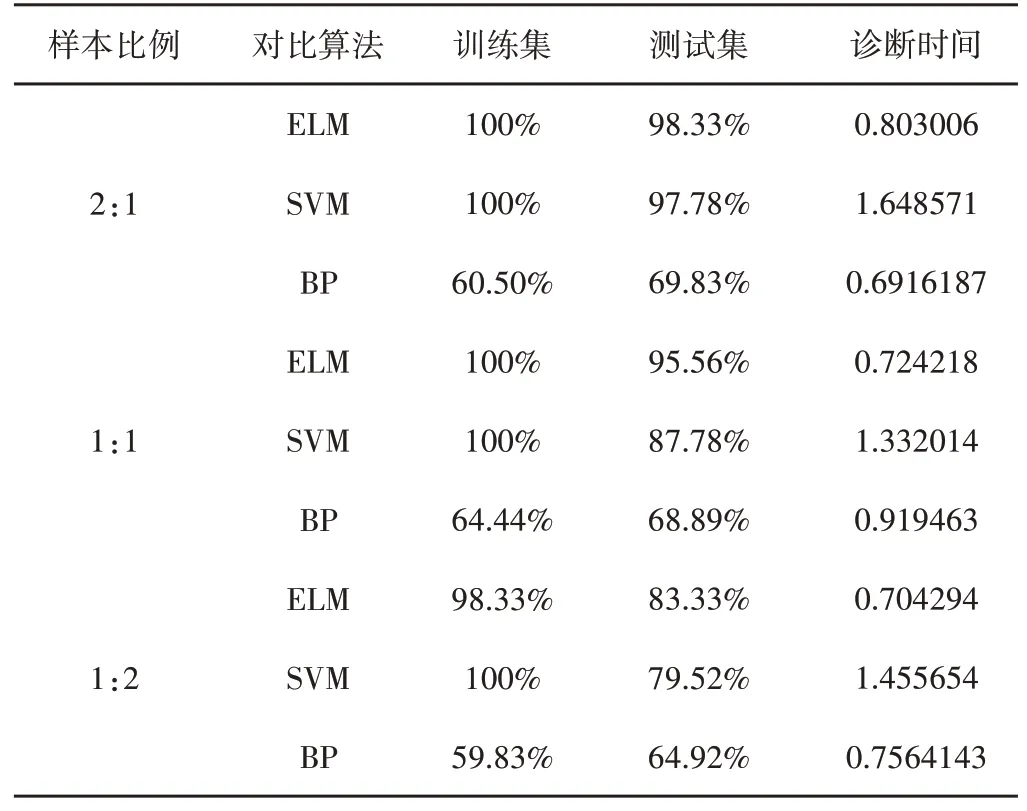
表5 诊断结果Tab.5 Diagnostic Results

由表5可知，ELM、SVM对滚动轴承故障的振动效果较佳；BP由于随机初始权值和阈值问题，导致结果较差；SVM由于是重复执行选择最佳结果，因此其效果较为理想；ELM网络能够逼近任意非线性函数，因此其诊断结果较佳。随着样本比例的递减，其诊断结果也逐渐变差；ELM和BP的平均诊断时间比SVM要低。综合诊断准确率和诊断时间，ELM网络相比其他对比方法效果明显，因此更适宜于轴承故障诊断。