结合HOG与SVM的电子元件多位姿目标检测研究

薄文嘉，倪受东

（南京工业大学机械与动力工程学院，江苏 南京211800）

1 引言

随着5G技术的兴起以及重点发展集成电路的政策提出，大量的电子元件需要在自动化生产线上被分拣、安装。其中视觉的目标检测算法系统在近几年来取得了飞速的发展，极大地提高了生产工作的效率，是研究的一个重要方向。

由于机器学习和深度学习突飞猛进的发展，目标检测技术研究的重点已经从传统的图像分割、模板匹配方式发展到特征提取结合分类器的方式，再到神经网络的方式［1］。现有的多位姿目标检测主要使用模板匹配的方式，此方式需人工提取目标特征，再制作模板，要耗费大量精力；并且算法受光照、阴影等因素干扰较大，鲁棒性差。

而神经网络的方式由于训练难度较高，计算资源开销较大，使此技术在多位姿检测的应用中受到了限制［2］。在大量算法中，方向梯度直方图（Histogram of Orientation Gradient）与支持向量机（Support Vector Machine，SVM）结合的算法方式因其泛化性能好，鲁棒性较强，训练难度较小，适合小样本而受广泛关注，现被尝试应用于多位姿目标检测中。

训练HOG-SVM分类器需要人工拍摄图像并制作相应的样本，这将投入大量精力。例如著名的PASCAL目标分类数据集，在收集和制作样本时花费了700个h［3］。因此研究出合适的训练样本数量，对于减少算法开发周期具有一定的参考价值。并且在现场使用0°角环形光源，供料器底部加装背光板，减少光照和阴影对目标产生影响的相对理想光照环境下，检测精确率初步要求达到65%以上。

考察到以上这些问题与需求，对目标检测分类算法进行了研究。通过机器学习，对振动供料器内摆放无规律，翻转后姿态高度相似并有可能重叠的小型电子元件利用HOG-SVM算法实现检测及分类。并且，分析了多组不同旋转角度提取的样本及其数量对于目标检测算法的影响，最终选取其中的最优结果使分类器性能趋于稳定，达到现场精确率要求。

2 系统方案设计

电子元件检测系统主要可以分为软件及硬件两个模块，硬件模块，如图1所示。主要包括：工业机器人，相机，振动供料器，光源等设备。相机使用Allied Vison工业相机获取目标图像，并且通过I/0线材连接到计算机。软件模块：基于visual studio 2015平台、运用MFC界面、使用OpenCV计算机开源库开发系统软件。

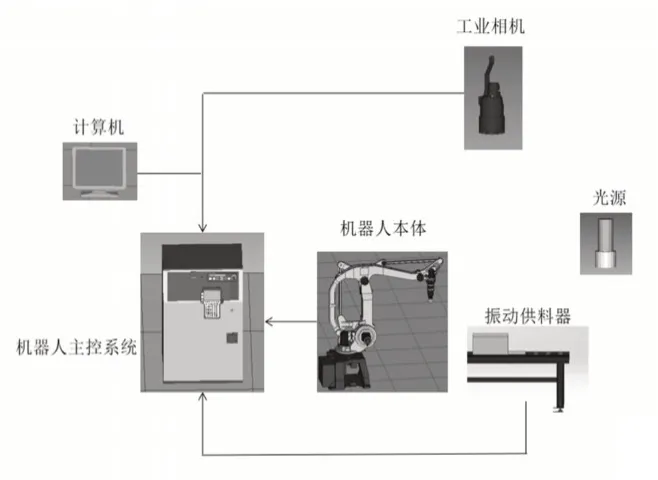
图1 系统硬件流程图Fig.1 System Hardware Flow Chart

机器人分拣系统的运作原理和过程为：当电子元件被放入振动供料器中后，通过计算机的控制，振动供料器对电子元件进行振动、翻转，然后相机在光源的配合下自动地获取电子元件图像，之后由分类器检测并分类出电子元件的正类姿态和负类姿态并得到正类姿态的图像坐标，通过坐标转换获得正类姿态的用户坐标，控制机器人对正类姿态的电子元件进行抓取；接下来再次控制振动供料器对剩余的电子元件进行振动并多次重复上述工作过程，最终将全部电子元件抓取分拣完毕，标志着系统的整个工作过程结束。

2.1 检测任务设定

待检测的电子元件以图2为例，此类元件体型微小，被振动翻转后的姿态相似度高，因此对检测算法的准确率与鲁棒性要求较高。

图2 电子元件示意图Fig.2 Electronic Component Schematic Diagram

元件被振动翻转后会出现如图3所示的5种姿态。其中图中所示1和2的姿态为正类姿态，标记为label=1与label=2。这两种正立的姿态会被机器人抓取、分拣以便于下一步的安装工作。图中所示的3、4和5姿态为负类姿态，标记为label=3，label=4，label=5。这三种姿态为非正立姿态，机器人会对此进行抓取分拣工作。

图3 电子元件姿态示意图Fig.3 Electronic Component Posture Schematic Diagram

检测系统首先会实时拍摄采集振动供料器中的元件获得图片，作为待测图像。通过机器学习对事先人工制作的样本进行学习，并训练产生分类器。将待测图像输入分类器中，实现图像分类，最后输出检测后的图像得到最终结果反馈给机器人控制系统。其工作流程，如图4所示。

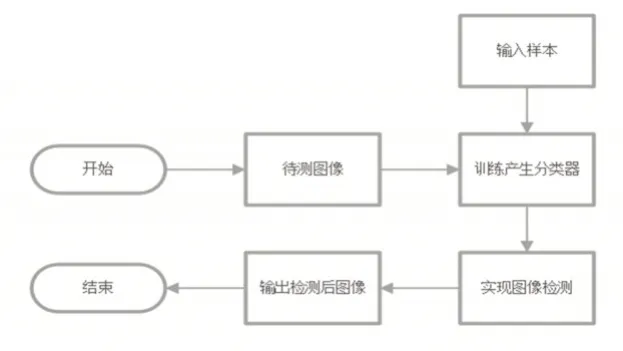
图4 检测任务工作流程图Fig.4 Inspection Task Workflow Diagram

3 视觉处理算法

3.1 支持向量机（SVM）

当训练样本是线性可分时，线性分类的SVM用一个超平面将两类样本分开，这个超平面是一条直线［4］。但在此类实际问题中，原始样本空间内并不存在一个超平面能将样本正确划分为两类。针对这个问题，要将原始空间的样本映射到更高维的特征空间中去，达到样本在这个高维特征空间内线性可分的目的［4］。

其中，φ(x)为x映射后的特征向量，那么，特征空间中划分超平面的模型表示为：

式中：ω、b-模型参数，由于该问题是线性不可分的问题，需要对此进行扩展，加入松弛变量ξi和惩罚因子c对错误分类的样本进行惩罚，从而得出解决线性不可分问题的模型：

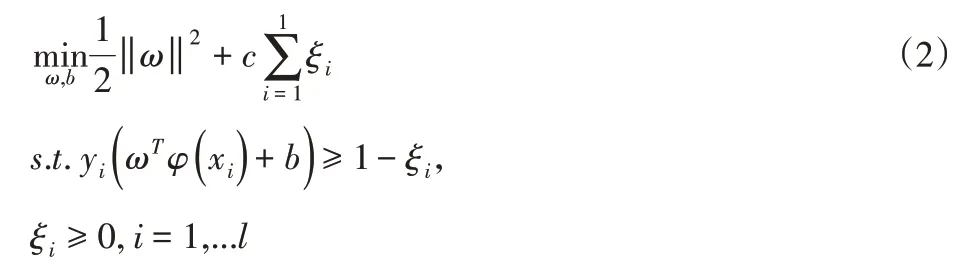
公式（2）本身是一个凸二次规划问题，可以对此式使用拉格朗日乘子法转化为对偶问题来进行更高效的求解，则对偶问题为：

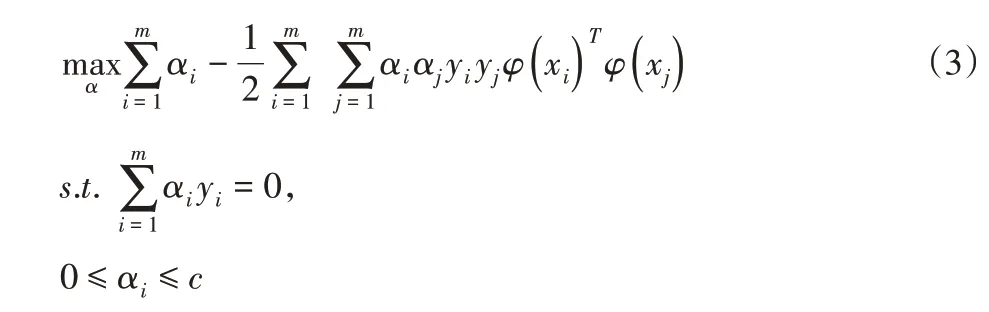
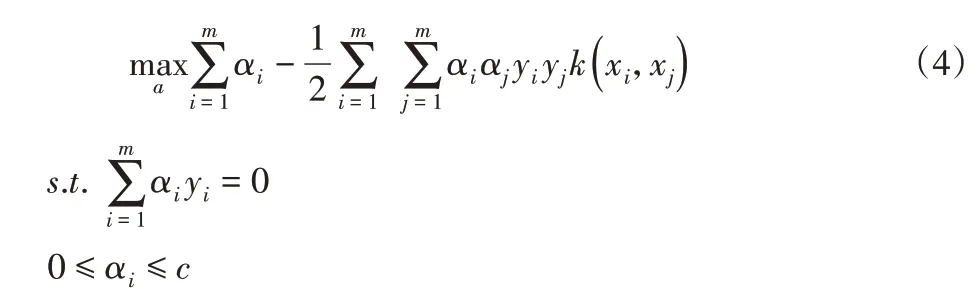
求解后得到预测时的分类判别函数为：

选用核函数为高斯核函数：

3.2 方向梯度直方图特征提取（HOG）

HOG特征提取是基于对稠密网格中归一化的局部方向梯度直方图的计算。它的基本思想是：即使不知道局部目标的外表与形状对应的梯度和边缘的位置，目标还是可以被局部梯度或边缘方向的分布很好地描述［6］。并且对于几何和光学变化都有很好的不变性。针对随意摆放，不同姿态的电子元件提取HOG特征的步骤如下：

（1）对图片进行预处理，剪裁图片并重新设置为固定大小。再用gamma参数压缩，归一化。

（2）进行梯度计算。先计算水平和垂直方向的梯度。事实表明简单的梯度算子结果最好，所以选用[ ]-1,0,1模板进行计算［7］。接下来使用下列公式（7）和（8）计算梯度的幅值g和θ。

图像中的梯度去除掉了许多不必要的信息，加重了电子元件的轮廓。

（3）计算方向梯度直方图。将一张图片分割成由多个8×8细胞单元（cell）组成的网格。此时使用无符号梯度，在这里0°和180°是一样的，所以将每个单元格中（0-160）°的梯度方向分为9个组距（bin）。对单元格中的每个像素基于它的方向组距进行投票，投票数值为像素的梯度幅值［8］。最后将每个细胞单元的直方图加在一起，得到整个图像的方向梯度直方图。

（4）对梯度做局部归一化。图片的梯度对光照的变化十分敏感，会造成梯度强度变化范围很大的结果［9］。为达到描述子块和光线变换无关的目的，要进行直方图归一化。将4个8×8的细胞单元组成一块（block），对这个16×16的块归一化，之后从图像原点开始以一个单元格为步长，向后移动遍历整个图像依次归一化。虽然在这个过程中，块之间的细胞单元被重复归一化，但是这样做明显会提升性能。

（5）0将每个block的梯度向量合并，得到整幅图像最终的HOG特征。

3.3 数据集

电子元件通过振动、翻转后以（0～360）°范围内的任意旋转角度随机散落在供料器内，散落姿态包括5种姿态。针对电子元件各不同角度的特征提取丰富程度以及样本数量对于算法性能的影响，提出以元件左侧边为轴，在（0～360）°的范围内，每逆时针旋转一个固定角度拍摄一个样本。如图5所示，为元件以第1种姿态旋转45°所得到8个的样本。

举例：基于特征b33a589d3627bc6f2e5bd0e6b42f 53b6，探测到URL http://198.98.122.172/cunty.sh，进而截取获得IP 198.98.122.172，针对这个IP进行端口探测和协议识别198.98.122.172:50

图5 样本示意图Fig.5 Sample Schematic Diagram

对5种姿态旋转5°、10°、15°、30°、45°来获取样本，最终得到5个不同特征丰富程度和样本数量的训练样本集，如表1所示。

表1 样本旋转角度及相应数量Tab.1 Sample Rotation Angle and Corresponding Quantity

3.4 元件重叠摆放检测阈值的确定

由于元件体积小，质量轻，且引脚之间有空隙，所以在振动翻转后极易出现元件重叠摆放的情况，影响算法对目标物体的分割，最终造成分类器的分类错误。在HOG特征提取完毕后，实际效果为加重元件的轮廓；假设待测图像分割后电子元件特征区域的像素面积为Tm那么：

式中：a，b-检测到电子元件轮廓区域的像素面积范围，在这个数值范围内的物体会被识别为元件重叠，从而不会进行分类，等待下次振动分离后，再次进行检测。在实验和生产的拍摄获取图像过程中，必须保持相机拍摄的深度始终一致，从而使得设置的像素面积范围与图像中目标物体的像素面积相匹配。

将a，b分别设置为100与550，当分类器检测到有目标元件的像素面积在此范围内时，会识别为元件重叠，避免分类错误，增强分类器的鲁棒性。

3.5 性能度量

对分类器的泛化性能进行评估，不仅需要有效的实验方法，还需要衡量模型的评价指标。对于二分类问题，可以将目标根据其真实类别与分类器分类类别划分为以下四种情况：

真正例（TP）：将正类分类为正类数，假正例（FP）：将负类分类为正类数；

真反例（TN）：将正类分类为负类数，假反例（FN）：将正类分类为负类数。

且对于分类问题常用的性能度量有［10］：准确率（Accuracy），精确率（Precision），召回率（Recall），F1度量。其中F1是基于精确率与召回率的调和平均，可用来度量分类器的整体性能。

4 实验结果与分析

实验检测在Win10操作系统下进行，CPU为Intel i5-7200U，主频为2.50GHz，内存8GB，使用VC++通过OpenCV进行编程。且实验在只使用小型0度环形光源，不加装背光板，使光照和阴影对目标产生相对影响的非理想环境下进行采图。将拍摄好的样本按不同姿态放相应的程序路径中，由程序缩放至64×64大小，并进行1764维的HOG特征提取，从而得到5种姿态的训练集样本。实验按照振动供料器所能放置目标物体数量的规格，设置每张待测图像中有20个电子元件。其中，label=1与label=2的两种正类姿态各5个，label=3、label=4、label=5的三种负类姿态共10个。之后由5个不同数量的样本集训练得到的分类器分别对待测图像进行检测分类，并将同一数量样本分类器分类记为1组实验。为减小偶然性对实验带来的误差，对同一个数量的样本集重复做5组独立实验，最终以5组实验的平均值作为实验结果。实验过程中所得到的检测后图像，如图6所示。

分类器会对图像中的电子元件形成外接矩，打上标签进行分类；并对第一种和第二种正类姿态标识出元件的质心，以便于下一步机器人的抓取工作。由公式（11）、（12）计算得到label=1和label=2两种正类姿态的精确率和召回率随样本数量变化的趋势，如图6所示。

图6 检测示意图Fig.6 Detection Schematic Diagram

如图7所示，横轴为样本数量，纵轴为精确率和召回率。从图7（a）可以看出，两种正类姿态的总体趋势基本一致，在样本数量较少时精确率都会出现不稳定和震荡。在第三个点当样本数量达到120个时整体变得稳定且呈现向上增长的态势；在样本数量超过180个后，精确率趋于平缓，几乎未再增长。同样，在图7（b）中两种姿态的召回率趋势与准确率大体一致。虽然在样本数量到达180个时，第一种姿态的召回率出现下降，但幅度非常小，在（120～360）数量的区间内基本稳定。可以看出，HOG-SVM分类算法对于第一种姿态的检测效果更好，精确率与召回率最高可达79.3%和64%；对于第二种姿态没有第一种高，但最终也能有67.3%的精确率和65.2%的召回率。说明不同检测对象对此种算法有一定的影响。

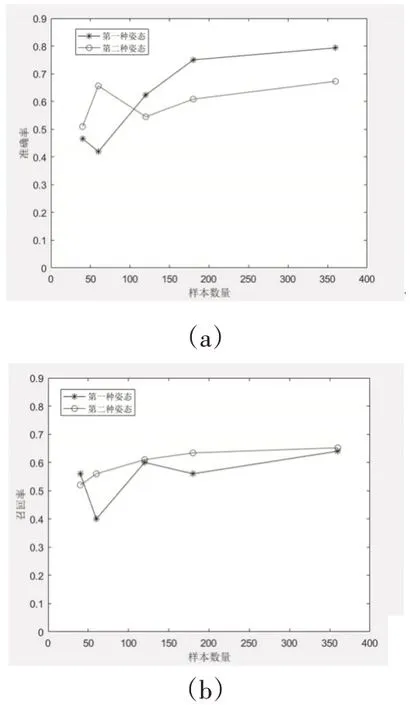
图7 样本数量-精确率和样本数量-召回率折线图Fig.7 Sample Number-Precision and Sample Number-Recall Rate Line Chart

通过式（13）得出F1，进行深入一步的分析，如图8所示。

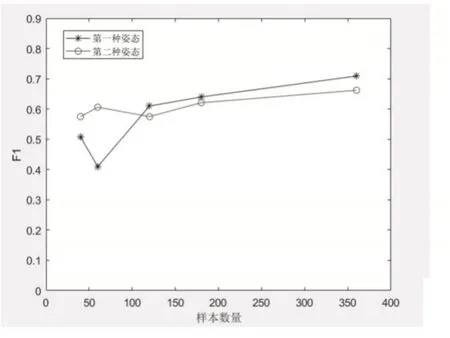
图8 样本数量-F1折线图Fig.8 Sample Number-F1 Line Chart

从图中得出，两种姿态F1折线的总体趋势与精确率、召回率趋势十分相似。当样本数量达到180个以后，F1增长速度变缓且呈现稳定的态势。

最后，使用对元件每隔10°旋转所得180个样本的样本集对元件重叠的特殊情况进行了实验检测，结果如图9所示。

图9 元件重叠检测图Fig.9 Component Overlap Detection Diagram

从图中可以看出，对于有接触以及交叉堆叠的元件，分类器未形成外接矩进行分割，并且未影响其他姿态的分类。因此，对重叠元件特征轮廓像素面积阈值进行设置，从而避免分类混乱这一方法是可行的。

5 结论

针对微小电子元件振动翻转以后姿态相似度高，元件重叠的分类检测问题，以及不同旋转角度获取的不同样本数量对开发成本和算法性能的影响；采用HOG-SVM算法进行了研究。经过实验发现，当样本数量达到180个以后，算法整体性能趋于稳定并在非理想环境下两种姿态的检测精确率分别为79.3%和67.3%，都达到了现场相对理想环境下精确率65%以上的初步要求。并通过对重叠元件特征像素面积阈值的设置，避免了分类的错误，增强鲁棒性。最终得出，每隔10°旋转获得的样本对目标的特征提取更加丰富，且由此得到的180个数量的样本集使得分类器整体达到了现场精确率的初步要求。实验仅在非理想环境下得出相应精确率，且第二种姿态的初步精确率相较于第一种姿态有差距；今后将在相对理想环境下进行实验，并优化SVM参数使两种姿态精确率得到进一步的提升。