超磁致伸缩驱动镜放大机构设计与仿真

2021-10-20闫洪波郝宏波

机械设计与制造 2021年10期

闫洪波，牛禹，高鸿，郝宏波

（1.内蒙古科技大学机械工程学院，内蒙古包头014010；2.包头稀土院，内蒙古包头014030）

1 前言

超磁致伸缩材料作为一种新型的功能材料，具有分辨率高、输出力大、响应速度快、能量密度高、频率特性好等诸多优点，在微电子技术、现代医疗机械以及航天航空等领域得到快速发展［1-4］。超磁致伸缩驱动镜作为建造大口径天文望远镜的核心部件，采用拼接镜面主动光学技术，通过传感控制对大量超磁致伸缩驱动镜进行精确定位来拼接成一块完整的巨大镜面［5］-［6］。由于天文望远镜对超磁致伸缩驱动镜的体积有所限制，导致其输出位移达不到使用要求，因此需要对输出位移进行放大。大量研究结果表明，柔性铰链具有体积小、免润滑、无间隙、无机械摩擦、运动灵敏性高等优点，常用于位移放大机构［7-9］。设计了一种基于杠杆式柔性铰链的二级微位移放大机构，用于超磁致伸缩驱动镜微小位移的放大。根据杠杆原理、静力学平衡原理推导出放大机构的放大率计算公式，设计放大机构各部分参数，通过有限元仿真和实验测试进行验证。

2 放大机构的设计

2.1 结构及工作原理

设计的杠杆式柔性铰链二级微位移放大机构，如图1所示。放大机构使用了5个柔性铰链，数量少、结构简单紧凑、负载能力强，且不改变位移的输出方向。

图1 放大机构结构图Fig.1 Amplifying Mechanism Structure

放大机构几何原理，如图2所示。驱动磁场推动超磁致伸缩棒产生位移，作用到杠杆上的S点，该位移作为放大机构的输入位移，经过二级放大后从P点输出。图中：l1、l3-位移输入端到支点的距离；l2、l4-位移输出端到支点的距离。

图2 放大机构几何原理图Fig.2 Amplification Mechanism Geometry

2.2 柔性铰链

柔性铰链是一种新型的机械传动结构，它的中部较为薄弱，在力矩的作用下发生弹性变形来实现位移的放大或运动的传递。但在实际的工作过程中，不仅会发生角变形，同时伴随着拉伸和压缩，导致柔性铰链的旋转中心发生偏移，影响机构的放大率［10-11］。

柔性铰链结构，如图3所示。图中：h-柔性铰链高度；b-柔性铰链宽度；R-柔性铰链圆弧半径；t-柔性铰链最小厚度，应满足h=2R+t［12］。

图3 柔性铰链结构图Fig.3 Flexible Hinge Structure

2.3 放大率的计算

设作用在柔性铰链i上的轴向力为Fi、轴向变形为Δi、力矩为Mi、转角为αi；又设杠杆j转角为βj。分析可知，α1=α2=β1，α3=β1+β2，α4=α5=β2。柔性铰链的受力与变形量关系和承受力矩与转角位移关系分别为：

其中［13］，

式中：KF-柔性铰链的轴向拉压刚度；KM-柔性铰链的转角刚度；E-机构材料的弹性模量；S-柔性铰链切割半径R与最小厚度t的比值。

首先分析第一级杠杆机构的输入、输出位移与受力情况。假设除铰链外的其他构件都是刚性变化，为分析方便，将铰链连接部分的作用力与反作用力用相同符号表示，第一级杠杆机构如图4所示。

图4 第一级杠杆机构图Fig.4 The First Level Lever Mechanism

第一级杠杆以铰链1为旋转中心，铰链1受到的拉力为F1，轴向伸长量为Δ1；铰链2在超磁致伸缩驱动镜的作用下，轴向压缩Δ2。X3为经第一级杠杆放大后的输出位移，Xin为磁致伸缩驱动镜的输出位移，则第一级杠杆的输入端位移X2为：

第一级杠杆的转角β1为：

对第一级杠杆进行受力分析，由受力平衡可知：

再分析第二级杠杆机构的输入、输出位移与受力情况。方法与第一级杠杆机构类似，第二级杠杆机构，如图5所示。

图5 第二级杠杆机构图Fig.5 The Second Level Lever Mechanism

第二级杠杆以铰链4为旋转中心，铰链4受到拉力F4的作用，轴向伸长为Δ4；铰链3连接两个杠杆，受到F3的作用力，轴向压缩为Δ3。Xout为经第二级杠杆放大后的输出位移，则第二级杠杆的输入端位移X′3为：

第二级杠杆的转角β2为：

对第二级杠杆进行受力分析，由受力平衡可知：

经两级杠杆放大后的输出位移Xout为：

联合以上各式，推导出该放大机构的实际放大率为：

其中，

根据公式（15）可以计算出该二级放大机构的放大率为7.98，计算时所用的参数为：l1=3.7mm，l2=10.5mm，l3=3.7mm，l4=10.5mm，R=1.2mm，t=0.6mm，b=1.2mm，该放大机构采用的材料为合金弹簧钢，弹性模量E=210GPa。

3 放大机构有限元仿真分析

3.1 有限元模型的建立

为验证所设计放大机构的正确性，使用ansys有限元软件对放大机构进行建模，采用四面体网格进行划分，因铰链圆弧切割处形变较大，对其进行细化处理，共划分网格118423个单元，24717个节点，有限元模型，如图6所示。

图6 放大机构有限元模型图Fig.6 Amplifying Mechanism Finite Element Model

3.2 边界条件的设置

对放大机构两边支座施加固定约束条件，在中间位移输入端以均布位移载荷方式进行加载，位移输出端不施加工作载荷，分析放大机构输出位移并计算放大率。放大机构变形图如图7所示，机构的输入位移作为初始条件，分别取5μm、10μm和20μm，通过仿真分析得到机构的输出位移如表1所示，根据输入与输出位移计算其放大率。

图7 放大机构位移变形图Fig.7 Amplification Mechanism Displacement Deformation

表1 输入位移与输出位移有限元计算结果Tab.1 Input Displacement And Output Displacement Finite Element Calculation Results

3.3 柔性铰链尺寸对放大机构的影响

柔性铰链尺寸的设计对放大机构起着至关重要的作用。改变柔性铰链的宽度b和圆弧切割半径R与最小厚度t的比值S，仿真其对放大率λ的影响，结果如表2所示。

表2 柔性铰链宽度b和比值S下放大率λTab.2 Flexible Hinge Width b And Ratio S Under Magnification λ

3.4 仿真结果分析

由图8可知，通过有限元分析得到的输入、输出位移与理论计算值基本相近，且呈现出良好的线性关系，放大率保持恒定。仿真分析所得的放大率为7.77，理论分析所得放大率为7.98，相对误差为2.63%，表明该放大机构位移损失小，结构设计合理。

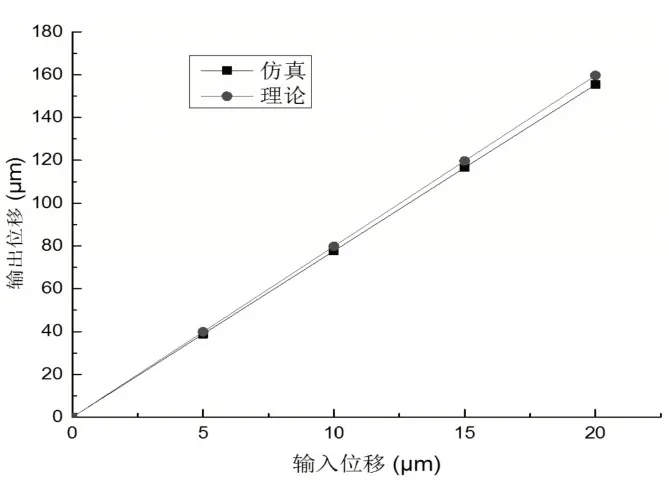
图8 输入与输出关系图Fig.8 Input And Output Relationship

由图9可知，随着柔性铰链宽度b增大，放大机构放大率呈现先缓慢减小后趋于稳定的趋势。根据图示变化，在满足制造条件的前提下，选择1mm左右宽度适宜。

图9 宽度b对放大率λ的影响Fig.9 Effect of Width b on Magnification λ

由图10可知，随着柔性铰链圆弧切割半径R与最小厚度t的比值S增大，机构放大率λ呈现先增大后饱和的趋势。根据图示变化，在满足最大应力小于材料的屈服极限的前提下，尽可能选择切割半径大、厚度薄的柔性铰链。

图10 R与t的比值S对放大率λ的影响Fig.10 The Effect Of The Ratio S of R And t on The Magnification λ

4 放大机构的实验测试

使用电火花线切割机床加工该放大机构，其总高度19mm，总宽度为17mm。为了避免放大机构因应力集中而影响寿命，切割中使用小电流档。放大机构焊接在超磁致伸缩驱动镜上，其实物及安装如图11所示。本次实验采用上海光炬仪器科技有限公司生产的GJ-IV型气浮自平衡精密光学隔振平台，输入位移由超磁致伸缩驱动镜提供。将安装有放大机构的超磁致伸缩驱动镜放置在平台的基座上，向其通入直流电流，分别测量输入端和输出端的位移，重复3次。