民用飞机复合材料帽型加筋夹角研究

何周理， 李旭辉

(上海飞机设计研究院，上海 201210)

0 前言

纤维增强复合材料由于比强度和比刚度高、抗疲劳和防腐蚀性能优异、可设计性等优点，在民用航空领域得到了广泛的应用[1-3]。飞机机身壁板是飞机的主要承力构件之一，而复合材料帽型长桁因为截面尺寸较大，且与蒙皮能形成一个闭合切面，使得帽型加筋壁板具有很好的稳定性，能承受较高的压缩载荷；复合材料帽型长桁的扭转刚度及弯曲稳定性能大大优于常用的“T”、“I”型剖面长桁[4]。所以目前波音787、空客A350 等多个民机型号在机身部位都大量采用了复合材料帽型加筋壁板结构[5-6]。

R.Vescovini和C.Bisagni等[7]研究了复合材料加筋壁板不同长桁(帽型、J型、T型和工型)的压缩和剪切稳定性能的差异；张绪等[8]通过试验和工程计算方法研究了复合材料帽型加筋壁板的承载能力；常楠、张铁亮等对加筋壁板通过两级方法进行优化[9-10]，张景新[4]、刘卫等[11]通过工程算法研究了复合材料帽型长桁截面尺寸的变化对承载能力的影响。

本文借助民用飞机复合材料帽型加筋壁板正向设计流程，首先通过工程算法确定了复合材料帽型加筋壁板的长桁夹角最优值，然后通过试验和有限元模拟研究了复合材料帽型加筋壁板不同长桁夹角的压缩承载力，验证了工程算法得到的夹角最优值的正确性。最后对比三种方法的结果，分析各方法之间的差异性，为设计师在帽型加筋壁板初步尺寸设计时提供参考，缩短研发时间。

1 帽型加筋壁板初步设计

复合材料帽型加筋壁板包括长桁帽顶、帽腰、帽缘以及蒙皮，组合形成一个闭合截面,如图1所示。此特性使得帽型加筋壁板具有较好的稳定性，能够承受较高的载荷。通常复合材料帽型加筋壁板的压损载荷要大于屈曲载荷，所以在初步设计时以初始屈曲载荷为依据设计帽型加筋的截面尺寸。

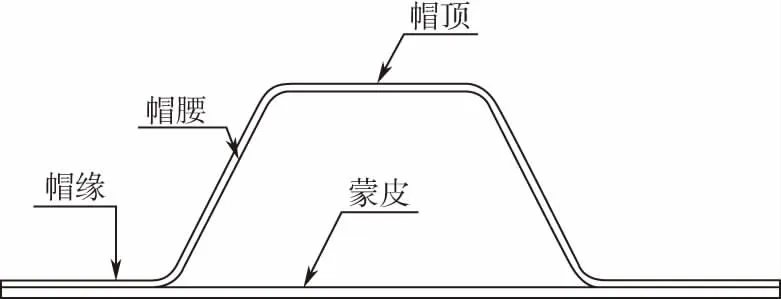
图1 帽型加筋壁板截面示意图

复合材料帽型加筋壁板的屈曲载荷工程计算方法采用文献[12]中的第9.2.1节中介绍的分析方法。凸缘的轴压屈曲载荷可按下式计算：

(1)

其中，Nxcr为单位宽度上的轴压屈曲载荷；bt为长桁凸缘的宽度；L为长桁的长度；D11和D66为层压板的纵向弯曲刚度和扭转刚度。

腹板的轴压屈曲载荷可按下式计算：

(2)

其中，bf为腹板的宽度；D12和D22为层压板的泊松弯曲刚度和横向弯曲刚度。

在初步设计时，将帽缘与蒙皮叠加部分看作凸缘，其两边可作一边自由，一边简支处理，运用公式(1)计算；帽腰、帽顶、帽底的蒙皮分别看作腹板，其两边简支处理，运用公式(2)计算；帽型加筋壁板按照上述方法可划分成6个单元，如图2所示。

图2 帽型加筋壁板单元示意图

按照公式(1)和(2)分别计算帽型加筋壁板凸缘单元和腹板单元的屈曲载荷，取凸缘和腹板6个单元单位宽度上屈曲载荷的最小值,参考文献[8]中的公式计算帽型加筋壁板的初始屈曲载荷，如下式：

(3)

其中，Pxcr为加筋壁板的初始屈曲载荷，t为屈曲单元的厚度，A为各单元对应的面积。

选取一段长600 mm的帽型加筋壁板作为研究对象，其中蒙皮、帽型长桁由Epsilon 99702.1/HTS-130碳纤维单向带共固化形成壁板。其中帽型长桁的高为30 mm，帽底宽60 mm，帽缘宽25 mm，其截面几何如图3所示。

图3 帽型加筋壁板截面尺寸

长桁铺层为: [±45/02/90/02/90/02/±45]，蒙皮铺层为: [45/-45/0/90/0/90/0/45/-45]s。采用文献[13]中的层合板的分析方法，得到各单元的弯、扭刚度(表1)。

表1 各单元弯、扭刚度

以帽腰和帽底夹角α为变量，α取值范围为[50 °,75 °]，按照公式(1)～(3)计算不同α角的帽加筋壁板的初始屈曲载荷，计算得到帽型加筋壁板屈曲载荷如图4所示。

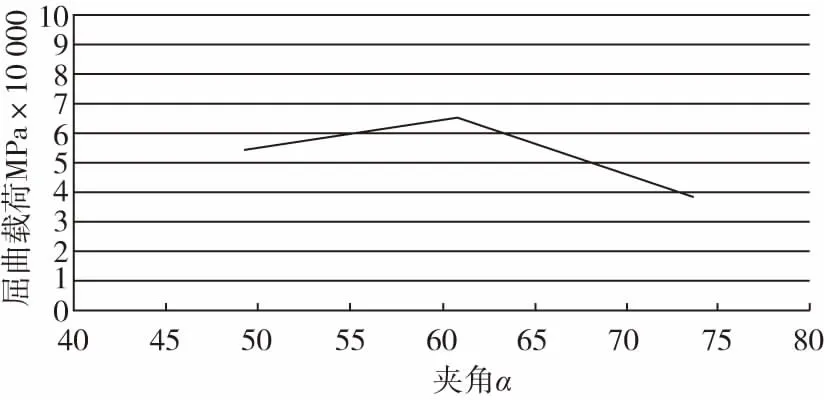
图4 屈曲载荷随α的变化曲线

通过工程计算可知：帽腰和帽底的夹角α在50 °～62 °之间时，屈曲载荷随着夹角α增大而增大；当α为62 °时屈曲载荷最大；随后α在62 °～75 °之间时，屈曲载荷随着夹角α增大而减小。所以针对本帽型加筋壁板的初步设计结果为：a为62 °时帽型加筋壁板承载效率最优。

2 有限元模拟

2.1 有限元模型

为了验证初步设计结果的准确性。分别通过有限元模拟分析和试验研究不同α角的帽型加筋壁板的压缩承载效率，取α角分别为52 °、62 °、72 °三种构型，如图5所示。

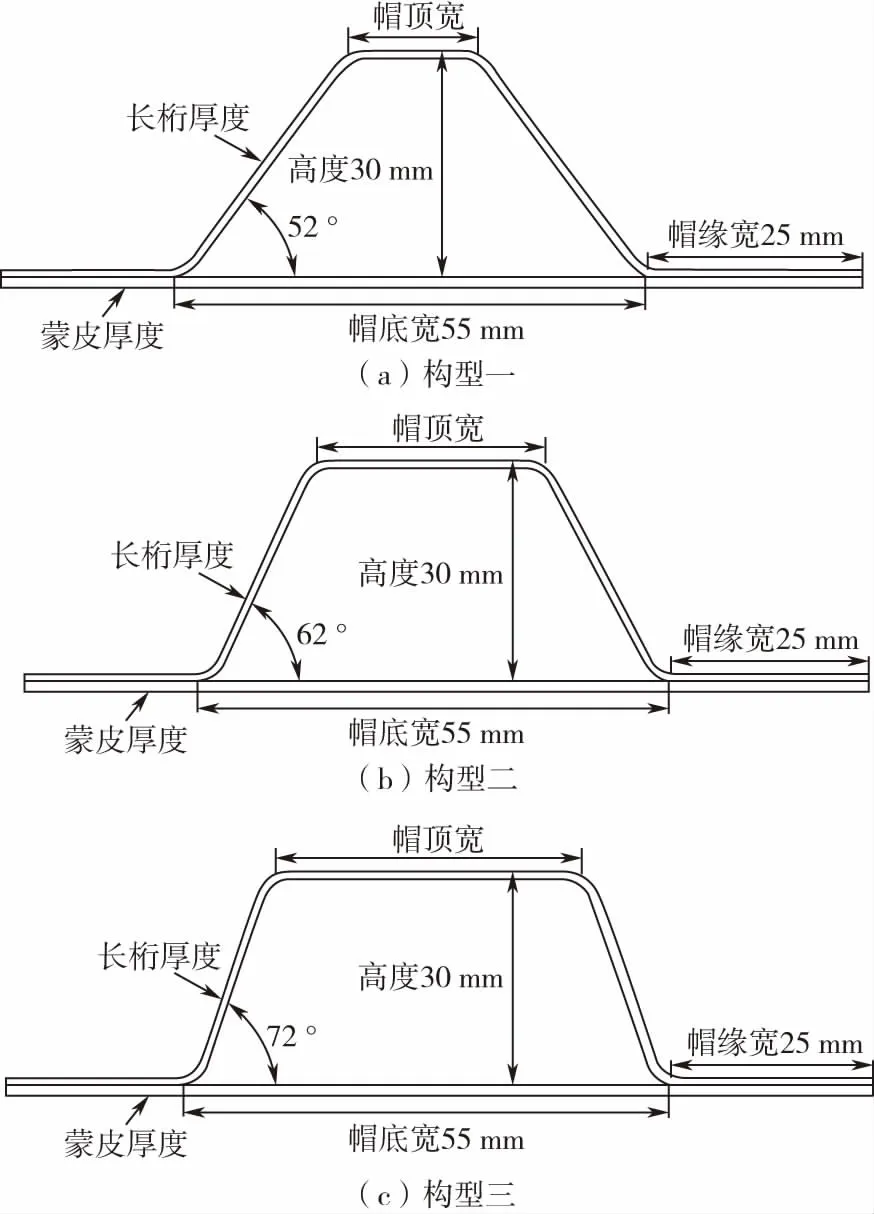
图5 三种不同夹角的帽型加筋壁板

根据帽型加筋壁板结构的几何尺寸、铺层信息建立有限元模型，并赋予相应的材料属性。壁板蒙皮、帽型长桁均用壳单元CQUAD4模拟。与参考文献[14]对有限元边界施加相同的边界约束，具体边界条件见表2。并施加沿长桁方向的压缩载荷P=10 000 N，根据帽型长桁和蒙皮横截面积的大小进行分配，将集中力均匀分配到加载端的节点上，有限元模型如图6所示。

表2 计算采用的边界条件

图6 有限元模型

2.2 有限元分析结果

通过有限元软件MSC.Nastran进行屈曲分析，经计算分别得到三种构型的一阶屈曲模态，按照公式(4)得到有限元分析的初始屈曲载荷：

Pxcr=λ×P

(4)

其中，Pxcr为初始屈曲载荷，λ屈曲特征值，P为压缩载荷。

三种构型的一阶屈曲模态结果如图7所示，有限元计算得到的屈曲特征值分别为8.829 4、10.467 2和7.751 1。然后按照公式(4)计算得到三种构型的屈曲载荷结果见表3。

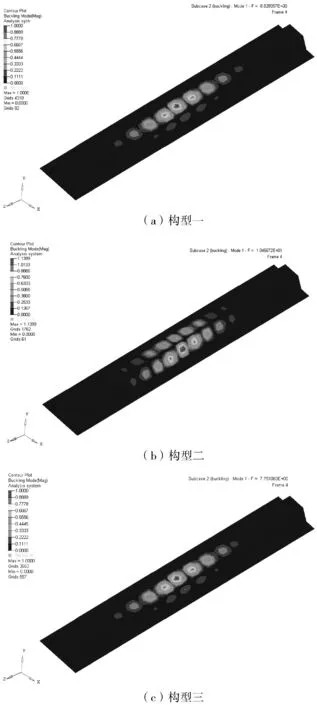
图7 一阶屈曲模态图

表3 有限元分析结果

有限元分析结果表明，在三种夹角构型的帽型加筋壁板中，夹角α为62 °时，屈曲载荷最大。

3 帽型加筋壁板试验

3.1 试验对象

试验测试构型与有限元分析构型一致，取α角分别为52 °、62 °、72 °三种构型，如图5所示。试验研究时，试验件两端各预留30 mm作为试验件夹持用，保证长桁实际承载长度为600 mm。由于复合材料强度性能分散性，每个构型试验件数量设计为6件，取平均值作为试验数据。试验件的加载接头仅施加纯压缩载荷，载荷均匀地作用在夹具上。夹具与试验件的连接形式如图8所示。

图8 帽型加筋壁板屈曲试验

在长桁四个不同截面的帽顶、帽腰、帽缘以及帽底蒙皮布置应变片。四个不同截面对应的位置以及应变片示意如图9所示。

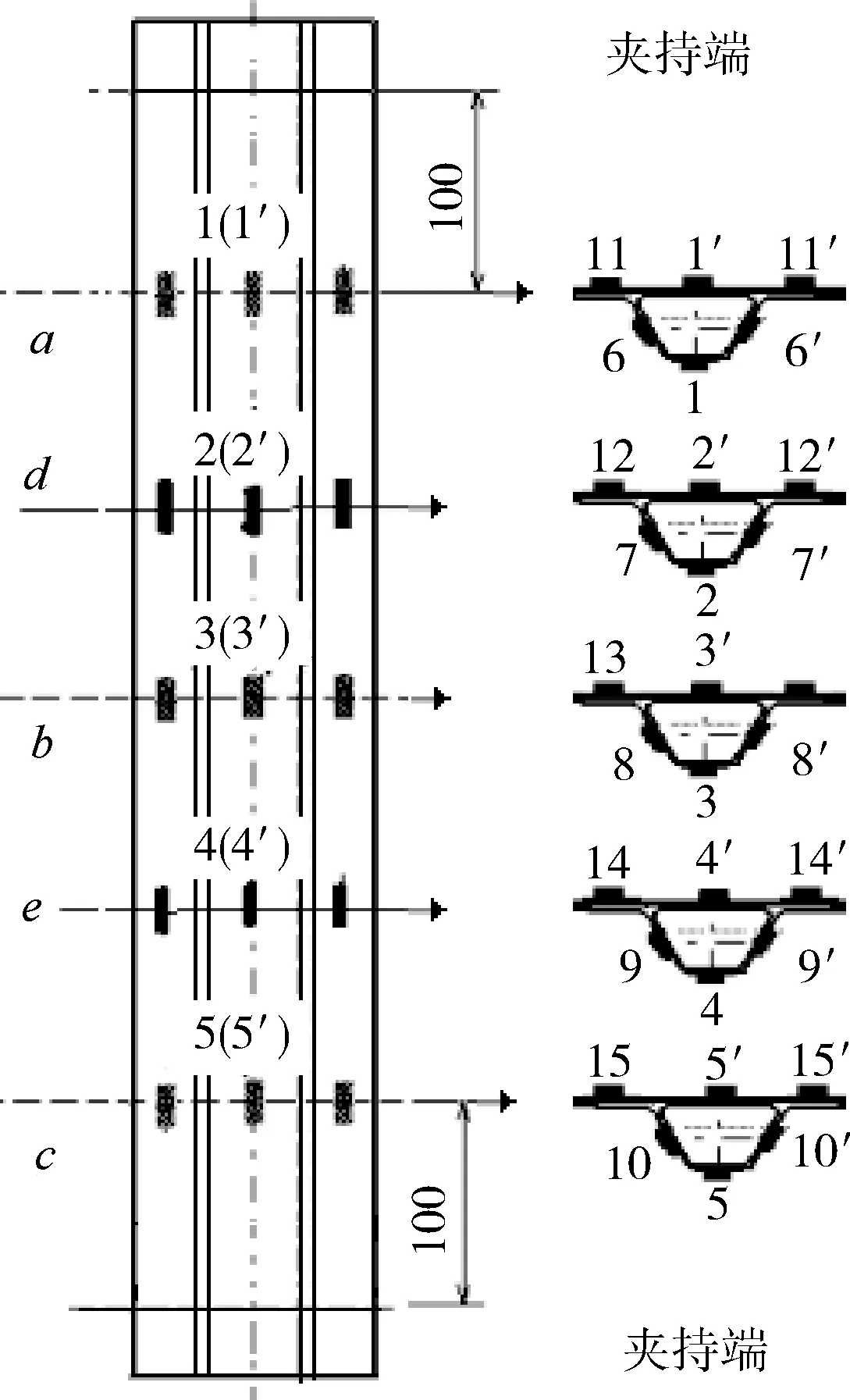
图9 帽型加筋壁板贴片示意图

3.2 试验过程

对帽型加筋壁板试验件进行静力压缩试验，记录加载接头的位移和力值数据，并观察试验件的变形情况。通过试验测量结果分析，确定每个试验件的初始屈曲载荷，比较不同α角构型的帽型加筋壁板的稳定特性(压缩承载能力)。

每次压缩试验前都需要进行载荷调试，保证施加的轴向载荷尽可能通过试验件形心而不引起额外的附加弯矩(误差5%以内)。压缩试验后，通过对试验机记录的力值和各应变片数据得到三种构型的帽型加筋壁板的压缩载荷-位移曲线。从四个截面的数据可知，屈曲首先出现在b截面处。图10～图12所示为b截面6个应变片对应的载荷-应变曲线，随着压缩载荷逐渐增大，应变数值呈线性增长，当出现拐点时即认为出现了初始屈曲。

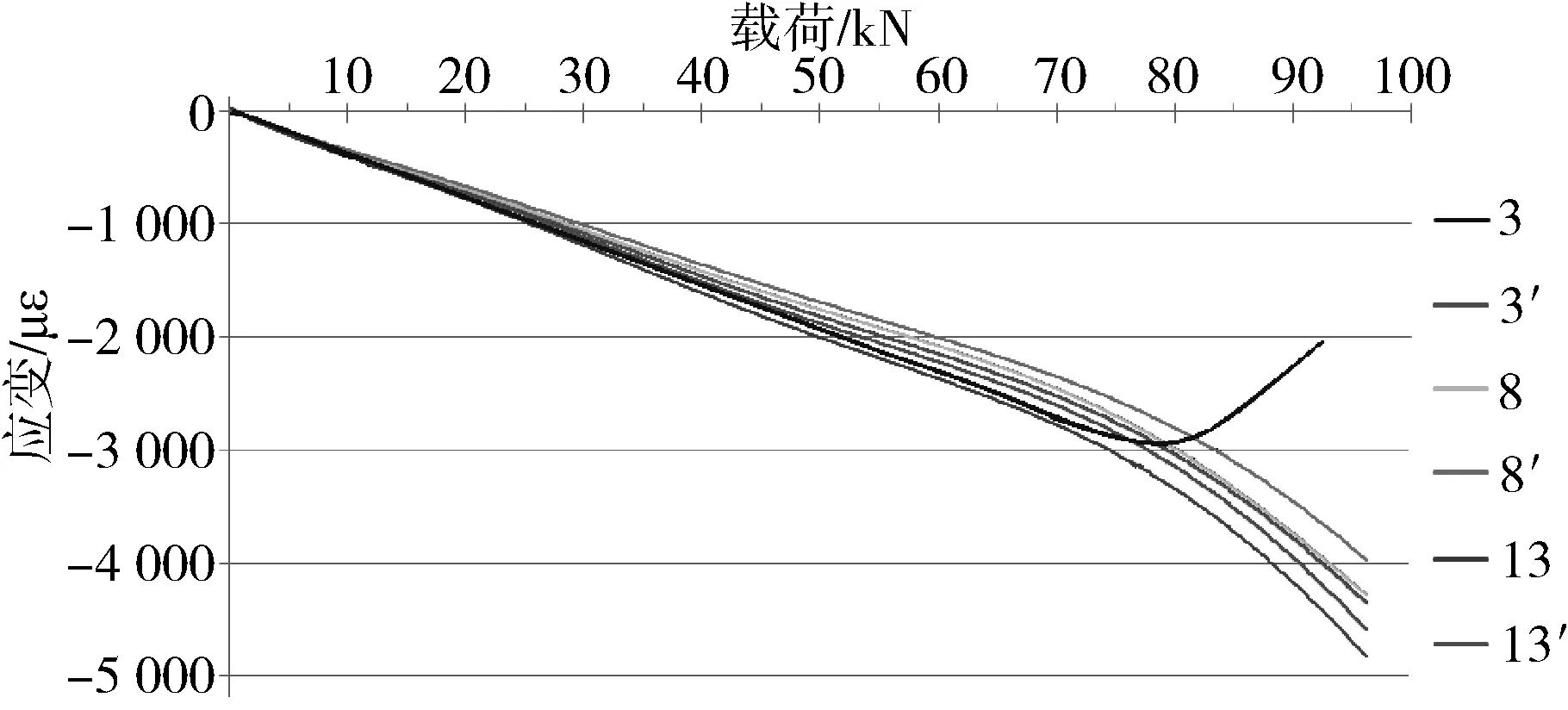
图10 构型一b截面应变片的载荷-应变曲线

图11 构型二b截面应变片的载荷-应变曲线

图12 构型三b截面应变片的载荷-应变曲线

由图10、图12 可知，构型一、构型三两个试验件随载荷增大帽顶最先发生屈曲，屈曲发生时对应的载荷分别为80 132 N、74 652 N；由图11可知，构型二的试验件随载荷增大帽腰最先发生屈曲，屈曲发生时对应的载荷分别为92 481 N。试验结果表明，在三种夹角构型的帽型加筋壁板中，夹角α为62 °时初始屈曲载荷最大。

4 结论

(1)对于帽型加筋壁板初始屈曲载荷，基于工程计算方法得出的最优夹角，通过有限元分析和试验验证了最优夹角的正确性。其中三种方法得到的初始屈曲载荷见表4。

表4 不同方法得到的初始屈曲载荷

(2)对于帽型加筋壁板初始屈曲载荷，有限元分析结果比试验值大，可能原因为有限元分析时不会出现偏心、试验件制造缺陷等因素。相对试验结果的偏差分别为10.2%、13.2%和11.3%，因此在飞机帽型加筋壁板初步设计阶段，可使用有限元分析作为强度校核方法之一。

(3)对于帽型加筋壁板初始屈曲载荷，工程计算结果比试验值偏保守，相对试验结果的偏差分别为27.3%、30.1%和31.8%。因此，在帽型加筋壁板初步设计阶段，使用工程计算方法可保证结构设计具有足够的安全裕度和设计余量，便于后续设计迭代。