锂电池SOC算法的研究进展
2021-10-20程琳瑞叶芯榕程桂石赵莹田伟
程琳瑞,叶芯榕,程桂石*,赵莹,田伟
(1.华北电力大学新能源学院,北京102206;2.华北电力大学控制与计算机工程学院,北京 102206;3.南京金邦动力科技有限公司,江苏 南京 211200)
0 引言
现代以来,全球各个国家尤其重视生态环境的可持续发展,开始从各个方面入手改善生态环境,减少污染。作为人类生产生活中不可或缺的交通工具,燃油汽车耗油量在石油总消耗量中占比较大。考虑到石油资源短缺,以及汽车尾气污染大气,新能源汽车应运而生,有望逐步替代传统燃油汽车,减少对石油的依赖,减轻对生态环境的污染和伤害。
动力电池是新能源汽车的关键部分,研究其相关特性对新能源汽车的发展具有重要意义。锂电池以其高能量密度、长循环使用寿命、较好的安全性等优势,在新能源汽车动力电池领域独树一帜。进一步提高动力电池的使用寿命和安全性,关键在于有一个更稳定、更精确的电池管理系统(BMS)。然而,电池管理系统的可靠性在于电池的荷电状态(SOC)是否更接近真实值。通过SOC可以判断是否需要对电池进行充放电,进而提高电池的循环使用寿命,提升用户的使用体验。但是,电池的SOC 值不能通过直接测量得到,只能通过其他直接测量得到的数据来进行估计,而且这些数据还会受电池温度、外界环境、电池老化度等因素的影响。当锂电池的SOC值在20 %~80 %之间时,开路电压非常平滑。如果仅依靠开路电压来进行SOC的估算,误差较大。并且,在不同工作条件下,虽然电池开路电压相同,但是实际的SOC值可能相差非常大。这就会使SOC的测量值与实际值有较大误差,因此需要不断提高SOC的估算精度,使电池管理系统更加可靠。
为了加快新能源汽车的发展,减轻环境污染,以及降低对石油的依赖,完善车用动力锂电池的管理系统,进而提高电池循环使用寿命和安全性尤为重要。解决这个问题的关键就是建立可靠的BMS。通过BMS对汽车电池进行科学合理化管理,使动力电池长期处于最佳工作状态,从而延长动力电池的循环使用时间,同时实时监管电池的状态,防止发生爆炸,提高安全性。而实现这些功能的前提需要更精准的测量出电池的实时荷电状态。本文中,笔者将主要介绍锂电池的SOC估算方法、发展现状,以及目前需要克服的困难。
1 锂电池SOC算法
目前,锂电池SOC算法主要有安时积分法、卡尔曼滤波法、双卡尔曼滤波法、扩展卡尔曼滤波法、无迹卡尔曼滤波法、神经网络法等。各种算法都有其优点和缺点。联合集合卡尔曼滤波的锂电池SOC估算方法[1],有效避免了高维矩阵的运算,提高了算法的效率和准确度。通过构建锂电池的非线性状态方程,出现了一种基于RC等效电路模型的锂电池SOC估计方法[2]。安装后经验证,该算法可有效降低SOC估计的误差。还有一种基于线性变参数(LPV)模型的电池SOC估算方法[3],是通过磷酸铁锂电池来进行实验的,也能有效减少 SOC测量值与实际值之间的误差。此外,因为未知噪声也会影响电池SOC估算的精度,所以一种将无迹卡尔曼滤波法和模糊推理相结合的模糊卡尔曼滤波算法[4](FUKF)应运而生。下面将介绍几种相对来说估算精度较高的算法。
1.1 扩展卡尔曼滤波算法
扩展卡尔曼滤波算法(EKF)是在卡尔曼滤波算法(KF 算法)的基础上将 KF 的高阶项忽略,仅采用一阶项,从而将非线性简化为线性。但是,EKF和KF一样,都是通过递推的方式来进行 SOC的估算,需要将前一次的计算结果带入算法再输出下一次的结果。每经过一次算法就会产生一些误差,进而造成累积误差。另一方面 EKF 算法忽略了温度因素对电池的影响,导致测量值不够准确。蒋聪等人[5]将影响电池工作效率的温度因素考虑进去,把由实验所得的真实数据和 Thevenin 等效电路模型相结合,拟合修改了其中的极化内阻、极化电容和开路电压的函数式,然后结合 EKF 算法,提出了随温度变化的 Thevenin 等效电路模型,再通过平方根分解来改进 EKF 算法,进而对电池的 SOC进行估算。实验结果表明,其最大误差和平均误差都在一定程度上减小了。
1.2 神经网络算法
一种基于 PSO-RBF 神经网络的锂电池SOC估算[6]被高俊岭等人提出。他们将径向基神经网络函数加以利用,与粒子群算法相融合,有效提高了算法的效率和自适应能力。特别是针对锂电池中变量之间的非线性变换,通过粒子群算法多次迭代,可找出其中最接近电池实际SOC值的函数值作为输出量。通过Matlab验证后,发现其预测结果比未加入粒子群算法的 RBF 神经网络算法的精度更高,更稳定。结果显示,预测值和实际值之差在4 %以内。
1.3 平方根无迹卡尔曼滤波算法(SR-UKF)
无迹卡尔曼滤波算法是将卡尔曼滤波算法中的非线性系统进行无迹变换来减小算法中的误差。在无迹卡尔曼滤波算法的基础上,章军辉等人[7]进行创新,提出了一种基于快速平方根的无迹卡尔曼滤波算法(SR-UKF)。他们对算法中的协方差矩阵取其平方根,进而避免了负值协方差矩阵,使算法输出值不发散,输出电池SOC的稳定值。此外,还有一种基于自适应无迹卡尔曼滤波的锂电池 SOC算法(AUKF)。董祥祥等人[8]通过改进的 Sage-Husa 自适应滤波算法保证系统未知噪声协方差矩阵的非负定性和对称性,通过实验发现 AUKF 的精度和稳定性都得到了提高。
通过查找相关文献资料,总结了锂电池 SOC几种算法的优缺点。扩展卡尔曼滤波算法简化了计算过程、缩短了算法时间,适用于任何工况,但是会出现累积误差,忽略温度因素对电池的影响,且收敛速度较慢[5,9-12]。神经网络算法的适应能力强,稳定性较好,鲁棒性强,但是易受干扰,需要大量的实验数据来训练模型,训练模型时易造成较大的误差[6,11,13-15]。平方根无迹卡尔曼滤波算法减小了输出值的发散,减少了非线性系统转换时误差,收敛迅速,但该算法计算量较大,算法较复杂,估算不准确[4,7-8,16-17]。
2 锂电池等效电路模型
建立的算法需要进行实验检验,但是如果均通过锂电池来进行实验验证比较繁琐。因此,人们建立了锂电池等效电路模型来进行替代,不仅能够有效进行算法的验证,而且可以节省实验步骤和时间。锂电池等效电路模型普遍应用,原因在于它方便应用和实验,便于理解和表示。现在主要有Thevenin 模型、Rint 模型、RC 模型、PNGV 模型等。下面将介绍几种常用的等效电路模型。
2.1 等效电池RC模型
二阶RC模型可以有效反映出电池内阻和电流对SOC的影响,具有很好的动态特性。它的特点在于当电池的电动势停止工作时,两端的电压 U不会瞬间突变为零,而是会在电容放电的作用下慢慢衰减至零。这与动力锂电池的特性相吻合。其大致电路如图1所示,包括两个串联的RC电路、电池内阻、电池电动势和开路电压。可以根据动力锂电池在停止供电后的实际电流、电压值来对图1中的参变量进行取值,进而得到锂电池的等效电路模型,用于锂电池SOC估算的实验。吴小慧等人[18]在《锂电池二阶RC等效电路模型参数辨识》中将电池模型RC参数的辨识问题转化为非线性最优化问题,从而建立出非线性最小二乘优化模型,并通过仿真实验发现消除了较大的误差项,得到了最优解。
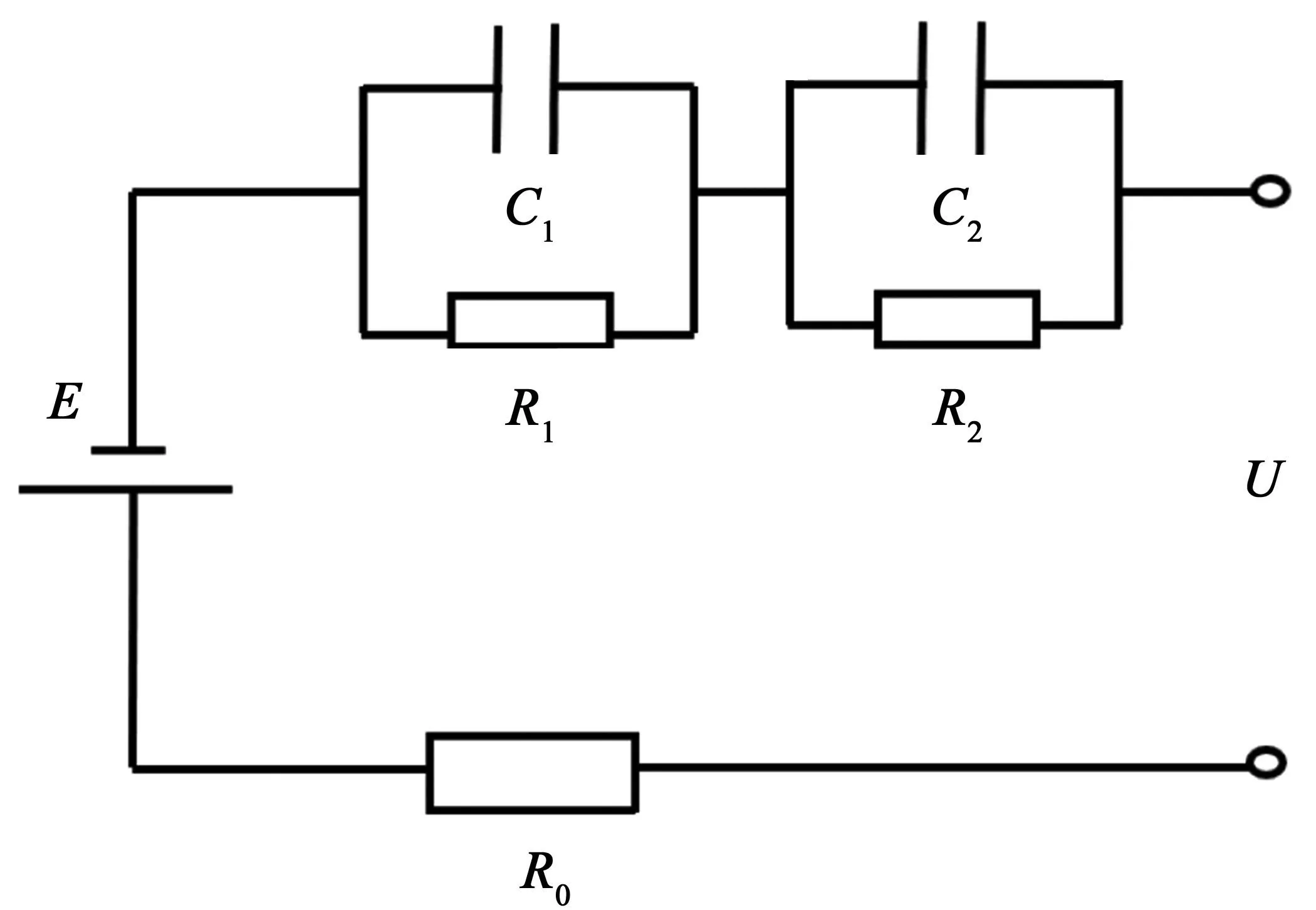
图1 等效电池RC模型
2.2 锂电池多项式等效电路模型
李文华等人[19]将圆柱形磷酸铁锂电池作为实验样品,通过多项式函数来进行电路参数与SOC的非线性关系转换,建立了锂电池多项式等效电路模型。通过对比实验所得数据发现多项式等效电路模型有很好的拟合性能,可以更好地展示SOC与电路参数之间的非线性关系,对提高电池SOC估算的精确度有很大的帮助。
2.3 动态Thevenin等效电路模型
在锂电池中Thevenin等效电路模型的应用也比较多,主要是因为该电路模型中的元件参数使用较少,如图2所示。相较于二阶RC模型,它只使用了一个RC电路。其中R、C和R0需要通过对电池进行放电实验测算得到。严利民等人[20]对 Thevenin等效电路模型进行了动态改进,将一阶 Thevenin等效电路模型和一组RC回路结合,改为了二阶Thevenin 等效电路模型,并将其中的欧姆内阻、极化内阻、极化电容和电池SOC联系在一起,通过函数连接,改为了动态变化。通过实验对比发现它的拟合效果更好。
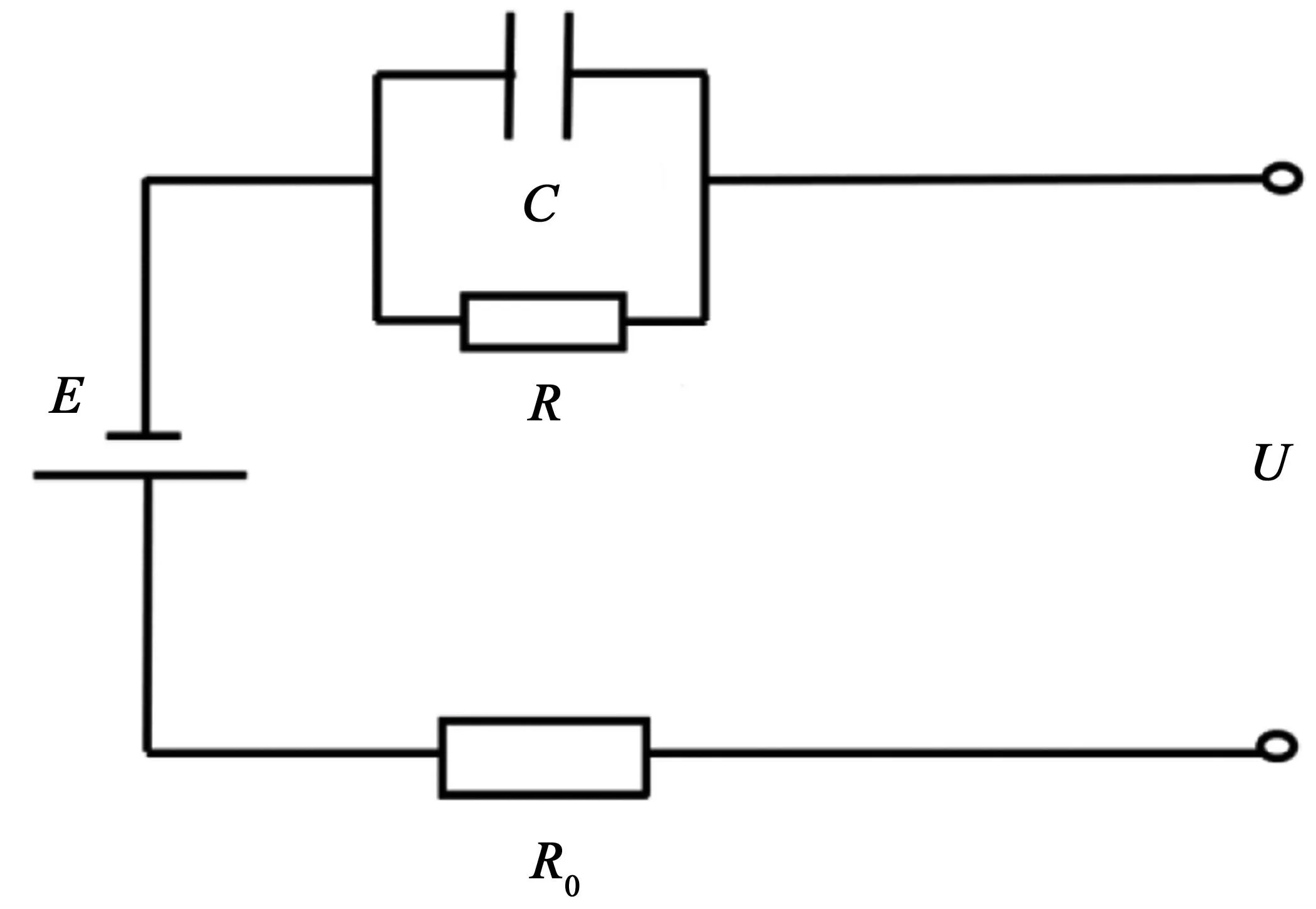
图2 Thevenin等效电路模型
对几个等效电路模型对比分析的结果如下:等效电池RC模型可以很好的模拟电池内部的化学特性、准确度较高,但它的参数辨识过程复杂,计算量会随阶数的增加而增大[2,18];锂电池多项式等效电路模型将电池处于低温条件下的化学特性变化考虑进去,具有很好的拟合性能,但其阶数较高,计算较复杂[19-20];动态Thevenin等效电路模型可以根据实时动态变化来拟合电池内部参数的情况,拟合效果好,参数易辨识,精度较高,但它的缺点在于不能完整描述动力电池的特性[16,21-22]。
3 结论
锂电池SOC值的估算方法多种多样,而且各有其优点和不足。总体来说,以卡尔曼滤波算法为基础所扩展的锂电池SOC算法相对较成熟,算法精度和稳定性都比较高,但算法的运算过程较复杂,还需不断完善。由于锂电池是车用电池,所建立的电池管理系统不能过于复杂,还需要考虑成本问题,电池的SOC算法估算时间也不宜过长,同时又需要保证精确度和抗干扰能力,还需要考虑外界因素,如温度、电池停机因素等,以及和电池自身的变化因素,如电池健康度。
新能源汽车相对来说具备良好的发展前景。如果车用电池的技术能够趋近成熟,新能源汽车的销售量和接受度将会大幅提升。笔者主要针对车用锂电池的SOC估算方法进行了系统地总结。随着技术研发不断深入,SOC 估算的误差将逐渐减小,精确度不断提高。相信在不久后锂电池的相关技术会趋于成熟,并广泛应用于市场。
