从深度教学视角谈中学数学思想培养路径
2021-10-20伍养群
伍养群
(福建省上杭县第一中学 364200)
高中数学涉及很多的数学思想,教学中提高学生对数学思想重要性的认识,培养其应用数学思想解题的习惯,对提高学生的学习能力具有重要的促进意义.为使学生能够灵活运用相关的数学思想,解答一些较为复杂的数学习题,应注重从深度教学视角开展教学活动.
一、明确目标,优选例题
函数与方程思想是高中数学中较为重要的数学思想.在深度教学视角下培养学生的这一思想时应注重结合学生的实际情况制定明确的教学目标,不能满足于学生运用该思想解答简单的习题,应注重通过例题的筛选、讲解,拓展学生的视野与能力,尤其鼓励学生做好听课的总结,归纳与牢记例题涉及的数学结论、规律,使其更加高效的解答数学习题.
例如,在讲解对数知识时,在课堂上为学生讲解如下习题:
已知方程xln3+xln4=xln5,则其正实数解的个数为( ).
A.0个 B.1个 C.3个 D.超过3个
解答该题需要对原方程进行整理,在函数与方程思想指引下研究对应函数的性质,而后通过观察得出结论.
令m=alogbc,n=clogba,两个等式的两边均取以b为底的对数得到:logbm=logbc·logba,logbn=logba·logbc,∴logbm=logbn,即m=n,alogbc=clogba.

二、积极互动,提升体验
数形结合思想是一种应用广泛的解题思想.从深度教学视角培养学生的这一思想时,应结合学生的已有知识储备做好相关例题的设计,尤其在讲解例题时应注重与学生积极互动,激活高中数学课堂,帮助学生理解相关的解题思路,提升学生的学习体验,掌握运用数形结合思想解答数学难题的相关思路.
例如,在讲解函数知识时,可围绕以下习题开展教学活动:

A.6 B.7 C.9 D.10
解答该题需要能够理解“y=f(f(x))”,而后画出函数f(x)的图象,运用数形结合思想进行解答.课堂上设计的互动问题有:(1)当x≤5时,函数f(x)的图象是怎样的,该怎样画出其图象;(2)函数y=log3x的图象和函数y=-log3(x+4)的图象有什么关系;(3)怎样理解“y=f(f(x))的零点”;当学生回答上述问题,便不难解答该题.
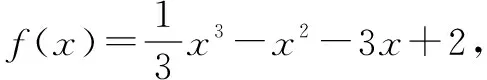
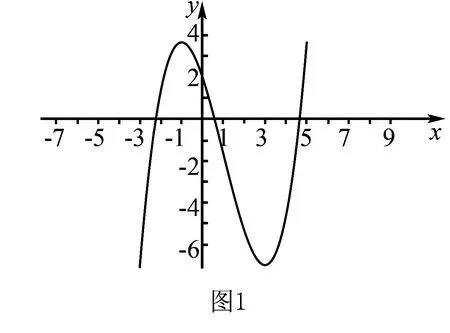
要求数y=f(f(x))的零点个数,即求函数图象y=f(x)和函数y=x1,y=x2,y=x3图象的交点个数.观察函数y=f(x)的图象可知,其和函数y=x1,y=x2,y=x3图象的交点个数分别为4个,3个,0个,因此,总的零点个数为7个,故选择B项.
三、注重鼓励,增强自信
建模思想是运用数学知识解答实际问题的一种重要思想.深度教学视角下培养学生的这一素养时应注重理论联系实际,通过设计生活化问题情境,定期组织学生开展数学建模比赛活动,尤其注重结合学生在数学建模中的表现,给予针对性的鼓励,使其及时找到建模的切入点,尝到运用建模思想解题的成就感,增强解题的自信心.
例如,在讲解函数知识时,可围绕以下习题开展建模比赛活动:

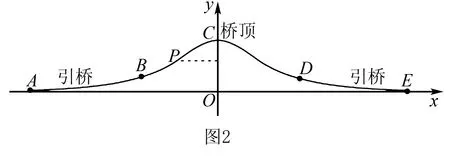

MP=|x-x0|f′(x0)(x0为P点横坐标)
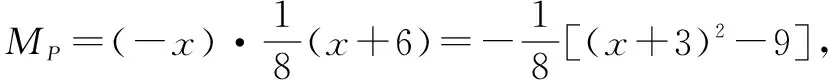
深度教学视角培养学生的数学思想时应牢牢把握“深度”二字,结合具体教学目标有计划、有针对性的开展相关的培养活动,尤其筛选教学例题、训练习题时做好难度上的把控,深化学生对所学知识认知的同时,更好的锻炼学生运用数学思想灵活解答数学习题的能力.
