核心素养背景下高中数学核心概念教学设计研究

焦随心

(甘肃省张掖市民乐县第一中学 734500)

数学核心概念作为高中数学学科要素之一，其贯穿于高中阶段数学教学的整个阶段.高中数学的教学之初，教师可经过数学的核心概念进行信息传递，通过数学的核心概念，促使学生充分领会到课堂的主旨，深入的学习各个章节的内容，以促使学生构成发散思维的同时，深入的了解与掌握相关知识点，并突破课堂教学中的重难点.在高中数学的课堂教学当中，数学学科核心概念的学习通常对学生的学习有着重要作用，其不仅需学生具备显著的逻辑思考力，而且还能促进学生自身的思维发散，从而使学生实现高效化学习，并促进数学课堂的教学质量的提高.

一、高中数学核心素养与核心概念

1.数学学科核心素养

数学学科的核心素养认知与掌握程度通常都能呈现出学生对生活当中应用数学知识、数学理论、数学逻辑进行问题解决的能力.通过抽象思维进行数、形、量的关键解决，可抽象得出一般的规律与结构；通过缜密化逻辑推理力，以演绎出事物的相关规律，并促进其普世化，或经过事物具备的一般规律对特殊化问题进行解决；通过直观想象思维对事物的规律与变化规律实施探究，以推测出事物反战的方向，对事物中的数学问题实施理解与解决；通过数学运算方法，对事物的运算规律、运算法则、运算思路进行提出，并以合理的方法开展运算操作，以获取到合理结果.《普通高中数学课程标准》当中对数学学科核心素养进行了明确界定，即数学抽象、数学建模、逻辑推理、数学运算、直观想象、数据分析共六个核心素养.

2.高中数学核心概念

依据数学学科的角度，核心概念主要指课程当中的概念，其概念主要是由核心概念所生成或与其有密切关联的.核心概念需满足下述条件：(1)知识属性是概念性，存在此阶段的数学概念体系当中，并在概念体系当中位于核心地位；(2)概念领域当中位于基础地位，有不能缺失的性质，存在概念范畴的最高层次，同时，核心概念还能把概念间的内在联系构建起来，以形成有缜密逻辑的概念程式.

二、核心素养背景下高中数学核心概念教学设计策略

核心素养下， 主要以任意三角形的核心概念教学为例进行教学设计，具体为：

1.基于情境设计的教学引入

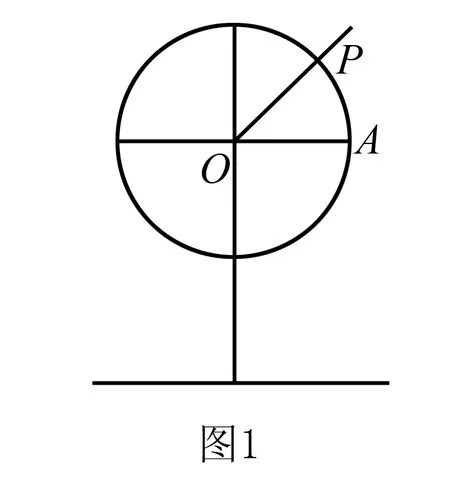
情境设计：乐园中的摩天轮，假设摩天轮中心点O与地面的距离高为20米，且绘直径为16米，沿着逆时针转动，转动一周所需60m秒，由A点进行转动，经过5秒之后，距离地面高度是多少米？如图1.

设计意图：周期现象是一个重要的数学模型，对于三角函数而言，其教学就需以三角函数的定义开始，因此，表面上为周期问题，其本质为三角函数定义问题.教师通过学生感兴趣、身边的素材，不仅有利于学生理解知识的发展，而且还能明白到数学属于生活的.

2.任意角三角函数定义讲解

教师提出问题1：任意角的三角函数该怎么定义？

设计意图：因为认识水平发展，指导学生把锐角三角函数推广至任意角三角函数，充分了解到定义需要修改，以促使学生在认知上形成冲突，调动学生的学习欲.如果已知应用原先的定义，就会影响到学生对知识的理解.

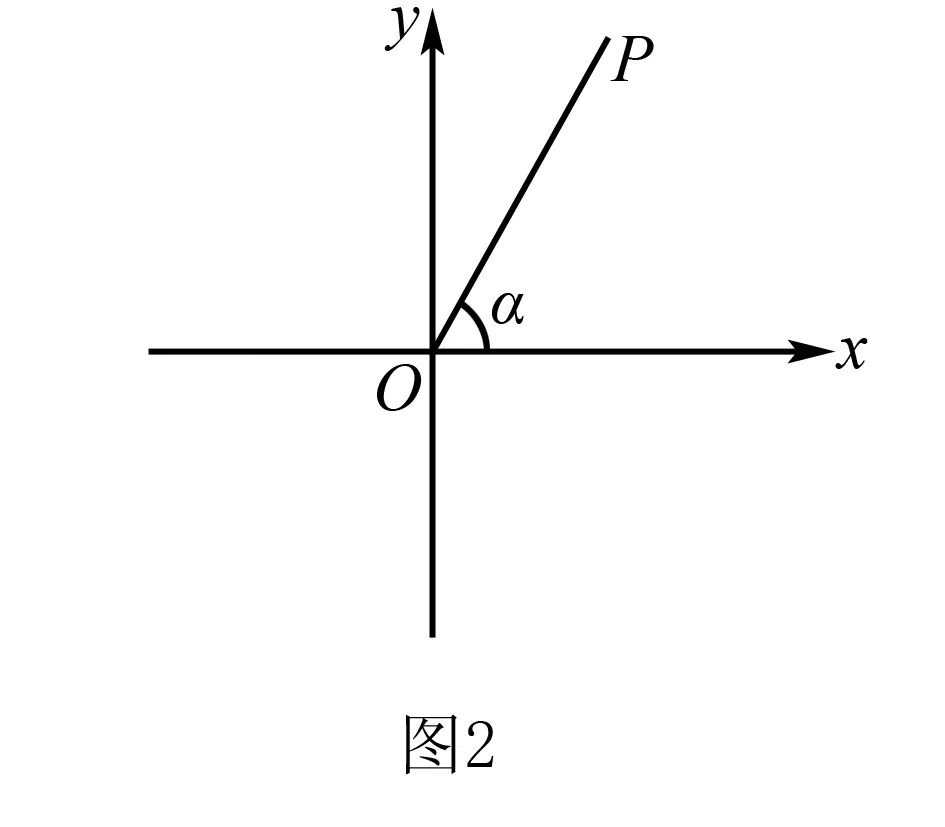
在实际教学中，可依据学生的具体状况，数学教师可通过相关问题链指导学生思考：(1)能否在直角三角形上对任意三角函数进行定义？该问题的设计主要是指导学生位于平面直角坐标系内对任意角三角函数进行定义.(2)在之前教学中，把锐角的概念推至任意角，将角置于哪里研究？教师可引导学生位于平面直角坐标系中对任意角三角函数进行定义，通过新观点充分认识到学生已具备的知识与经验，并促进新知识迁移作用的发挥，把新知识和学生原先具备的知识经验相联系，从而使学生实现高效学习.(3)图2位于平面直角坐标系当中，应该怎么定义任意角三角函数？由图2可知，角α终边位于第一象限，学生通过潜移默化，就能够认识到角α为锐角，因此，学生仍选择直角三角形的边长比值进行定义.此时，数学教师就需加以引导.(4)通过几何画板，教师可给出角α终边落在射线OP上，那么终边在OP的角必是锐角吗？若不是，可通过直角三角形边长对角α三角函数进行定义吗？又如图3，若角α的终边不是在第一象限，又应该怎么处理？(5)通过平面直角坐标系，可以使几何问题转变成代数问题，如点能够通过坐标进行表示，而直线能够通过x、y的函数关系式进行表达.现将目光聚焦于锐角三角函数定义上，是否含有其他的定义方法？

问题(4)与问题(5)进行组合设计的主要目的是融入数形结合思想，在初中的时候，定义三角函数的时候，就会用到图形，而高中阶段在定义的时候，仍旧运用图形.

(6)通过平面直角坐标系当中的角位于终边上点的坐标以三角函数进行表示有什么优点？

通过该问题的设计，教师就能给出下述式子：

sinα=y/PO，cosα=x/PO，tanα=y/x.

本节课的设计虽然花费了较多时间，但却很有价值，由于在核心素养下，将课堂全部交给学生，其满足“以生为本，以教师为主导”的课堂教学理念，而学习核心概念则需呈现出数学知识的前因后果，不能只是将结论告诉学生，这会使学生丧失学习的主动性.此时，为了使学生继续学习，并联想到直角坐标系具备的作用，教师可立即将学生引入下个方向：引出单位圆.

教师提出问题2：同学们，有什么办法能够使定义的获得更加简洁？

设计意图：通过坐标进行三角函数值的表示已较为成功，由于函数属于数集与数集的对应关系，比值虽然也属于数，但仍旧有一定区别，对学习三角函数的图像、线都存有障碍，因此，需做出相应的改变，这种改进通常表现为教材编者自身的智慧，而问题设计也是为了实现单位圆的引入做出铺垫.对于单位圆的引出，主要反映于：①单位圆具备的作用能够反映出对任意角进行理解；②单位圆能够很好的呈现出数形结合思想.通过数形结合的数学思想，把直角坐标系与单位圆组合，其和定义有着密切联系.

教师提出问题3：同学们，是否能够定义任意角三角函数？

教师可引导学生探究：假设任意角α终边和单位圆的交点是(x,y)，那么sinα=y，cosα=x，tanα=y/x.

设计意图：主要是依据以生为主的原则，并通过单位圆，基于锐角三角函数，对任意角三角函数的定义及合理性进行探究，以促使学生将三角函数的相关知识融入到函数内容中.

综上所述，高中数学时期的核心概念教学中，通常对数学教学有着重要影响.因此，数学教师在课堂教学时，可通过数学核心概念的教学案例，培养学生的数学学科素养，并对数学教学模式实施创新，从而使学生自身综合素质得以提高的同时，实现数学课堂教学质量的提高.