颗粒形状对珊瑚砂和石英砂沉降影响的试验研究

金智涛，郑建国，张君，王锴锴，李杰，许国辉

（1.中国海洋大学 海洋环境与生态教育部重点实验室，山东 青岛 266100；2.中国海洋大学 山东省海洋环境地质工程重点实验室，山东 青岛 266100；3.中国海洋大学 环境科学与工程学院，山东 青岛 266100）

泥沙的运动特性与河道、航道淤塞（唐鸿琴等，2019）、海岸侵蚀（林峰竹 等，2015）、海底浊流的形成（Heerema et al，2020） 等密切相关，而泥沙沉速作为一个最直观的物理性质，受到了广泛关注（沙玉清，1956），在研究携沙、航道整治、能力、浊流机制时都需要准确的泥沙沉速（赵德招等，2009）。在沉降方面，较早由牛顿提出了紊流区的绕流阻力公式，之后Stokes 推导了层流下球体的沉降公式。但在力学机制较为复杂的过渡区，很难从理论上推导一个适用的公式，故有较多学者如沙玉清、张瑞瑾、窦国仁、岗卡洛夫等，进行了大量试验，对结果进行统计后，得到了精度较高的经验公式（茹玉英等，2010）。这里需要指出，各家所推导的过渡区沉降经验公式都是以球形作为基础，但天然泥沙的形状与球形之间存在差异，这对泥沙的沉速有很大的影响（李大鸣等，2004）。故需要进行大量的试验，以确定形状影响下的阻力系数，提高公式的精度。当粒径继续增大至紊流区（d > 2 mm），颗粒不同的形状如球形、盘形、柱形、棱形等对沉降的影响不同，需要分别讨论（沙玉清，1965），有关砾石的运动特性韩其为等（1999）进行了较为细致的工作。

珊瑚砂是一种钙质砂，常见于我国南海诸多岛屿（于红兵等，2006）。与陆源石英砂相比具有比重大、磨圆度低、形状不规则等特点（王新志，2008），使得其在动力学上具有不同的运动特性（荀涛等，2009；陈松贵等，2018）。以往对于泥沙运动特性的研究主要针对石英砂，对于珊瑚砂的研究较少，正确认识珊瑚砂的运动特性对南海诸岛的开发有着重要的意义（刘亮等，2015；王初升等，2012）。

宏观上珊瑚砂和石英砂的区别十分明显，在微观上如棱角度、孔隙也存在明显差异（陈海洋等，2005；周博等，2019），因此对于采用石英砂的沉速公式计算珊瑚砂沉速并不合适。也有学者对两种砂的起动特性进行了试验（周乐序等，2015；邹俊飞等，2016），结果同样表明二者在起动上也存在着不同。荀涛等（2009）在使用石英砂的沉降经验公式计算珊瑚砂（粒径为0.6～1 mm）的沉速时，发现粗粒径的珊瑚砂实际沉速小于计算值，这代表石英砂的沉降经验公式不能较准确地计算珊瑚砂的沉速。吴野等（2018）考虑了珊瑚砂在形状上的特点，通过沉降试验建立了珊瑚砂的拖曳力模型，比传统拖曳力模型计算珊瑚砂拖曳力精度更高。

本文选取珊瑚砂和石英砂两种不同的砂体进行沉降试验，对试验数据进行统计分析，给出动力形状因子茁，描述形状对两种砂体沉速的影响，通过对沉降数据的分析，提出了一种适用于珊瑚砂的沉降公式，以期为珊瑚砂质岸滩的保护以及珊瑚砂的工程开发应用提供参考。

1 室内试验

对于天然泥沙形状不规则这一问题，常通过拟定一个参数来表示颗粒形状和球形的差异，如球度（Wang et al，2020）、长宽比等，在工程上常用长宽比这一参数（Ardekani et al，2016）。为研究在过渡区形状对珊瑚砂沉降的影响，本试验以粒径处于0.1～1 mm 之间的无黏性珊瑚砂和石英砂为研究对象，统计砂粒的长宽比，同时为分析黏度对沉降的影响，分别在体积分数为33%的甘油溶液和水中进行沉降试验。

1.1 试验材料与设备

珊瑚砂取自南沙群岛，石英砂取自青岛市石老人浴场，均筛取粒径范围在0.1～1 mm 之间的颗粒用做试验。试验设备包括：（1）比重瓶和真空抽气泵。（2）体视显微镜（型号为Nikon SMZ1500）。（3）外侧标有刻度的透明亚克力直筒（图1），其直径为14.5 cm，高度为140 cm。（4）佳能800D高速摄像机（30 帧/s）。（5）R/S+流变仪（Brook原filed 工程实验室生产），使用同轴转子（型号为MK3-CC40-DIN）及配套样品杯。

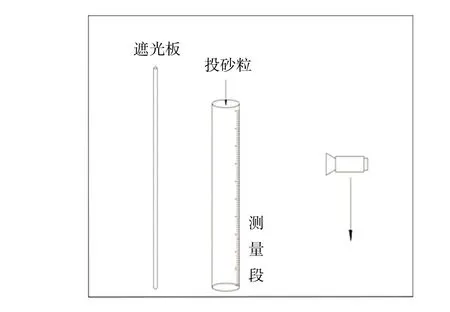
图1 试验装置示意图

1.2 试验方法

试验前用比重瓶法测量珊瑚砂和石英砂的比重。采用单颗粒沉降的方法，沉降试验所用砂粒在供试验所用珊瑚砂和石英砂中随机选取。使用体视显微镜对挑选砂粒粒径进行测量，测量精度为1 滋m，砂粒粒径涵盖了0.1～1 mm 的粒径范围。将测量后的砂粒平稳放置于直筒水面，使其以零初速度自由下落，并对下落全过程进行录像。录像结束后重新挑选砂粒进行粒径测量和沉降试验。后续通过录像计算砂粒在其下落过程中的稳定沉速（图2）。

图2 珊瑚砂和石英砂粒径测量

在试验过程中，为比较液体黏度对沉降的影响，采用两种不同黏度的流体进行对比试验。低黏度的流体选用清水，高黏度流体选用稀释后的甘油（体积分数为33%）。选用甘油的原因是甘油属于牛顿流体，能与水以任意比例互溶，与水互溶后黏滞系数变化大。使用流变仪对两种液体黏度进行测量，流变试验和沉降试验均在室温下进行，可忽略温度对黏度的影响。具体试验粒次如表1。

表1 试验粒次

2 试验结果

珊瑚砂和石英砂比重测量平均结果分别为2.84和2.64。在体视显微镜下对试验所有用砂（598粒）进行粒径测量。为了减少形状对粒径的影响，选择短轴径表征砂粒粒径，同时计算长宽比琢（长轴径比短轴径）。流变试验结果如图3 所示，黏度为剪切应力与剪切速率之间的比值。甘油溶液黏度为0.002 6 Pa·s，水黏度为0.001 Pa·s。

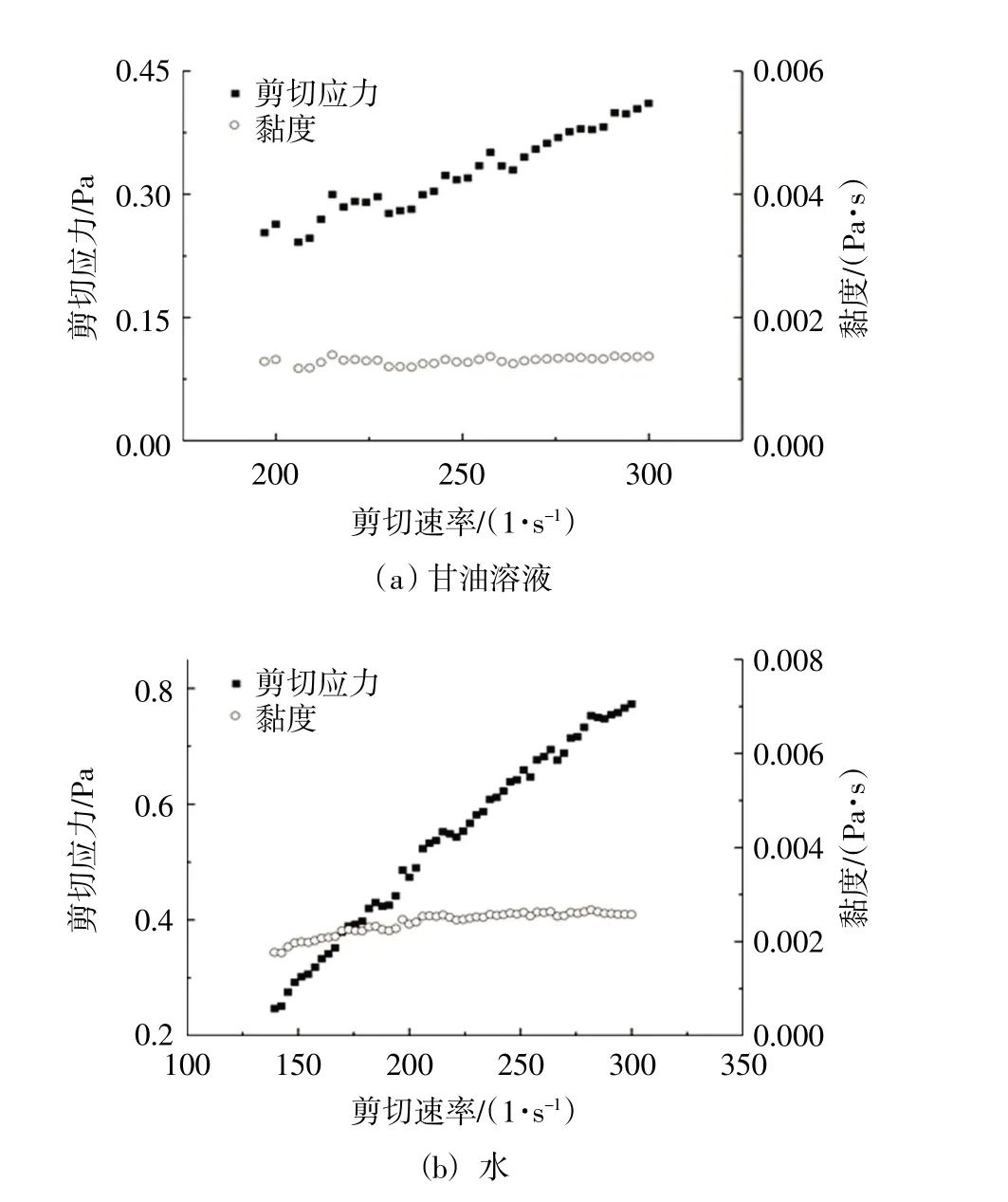
图3 流变试验结果

珊瑚砂的比重大于石英砂，因此由经验公式计算得出的珊瑚砂沉速要大于石英砂，但试验结果显示珊瑚砂沉速并未明显大于石英砂，反而在甘油溶液中石英砂沉速最大值大于珊瑚砂，这说明形状影响了砂粒沉降，且对珊瑚砂起到的影响比石英砂大。

将某一颗粒粒径d 作为横轴，长宽比琢作为纵轴，将该颗粒的沉速数据标记于二维平面图中，所有颗粒沉速数据如图4。以图4（a）为例：在过渡区的泥沙沉降经验公式中，泥沙沉降速率与粒径d 和ln 琢呈正比，和琢呈反比（童祜嵩，1989）。图中线段a 代表了理论公式中同一沉速下长宽比和粒径的关系。分析线段a 能够发现当长宽比超过1.5 后，长宽比对沉速并不会造成明显的影响，而试验结果显示此时沉速仍受到形状的影响。同时对比图中实际等沉速线，能发现在粒径较小时，沉速与粒径和长宽比的关系符合该经验公式，随着粒径的增大，偏离程度也愈发严重。故仅用长宽比这一参数无法将珊瑚砂形状对沉降的影响进行较好地描述，对于珊瑚砂需要提出新的参数，来描述形状对沉速的影响。

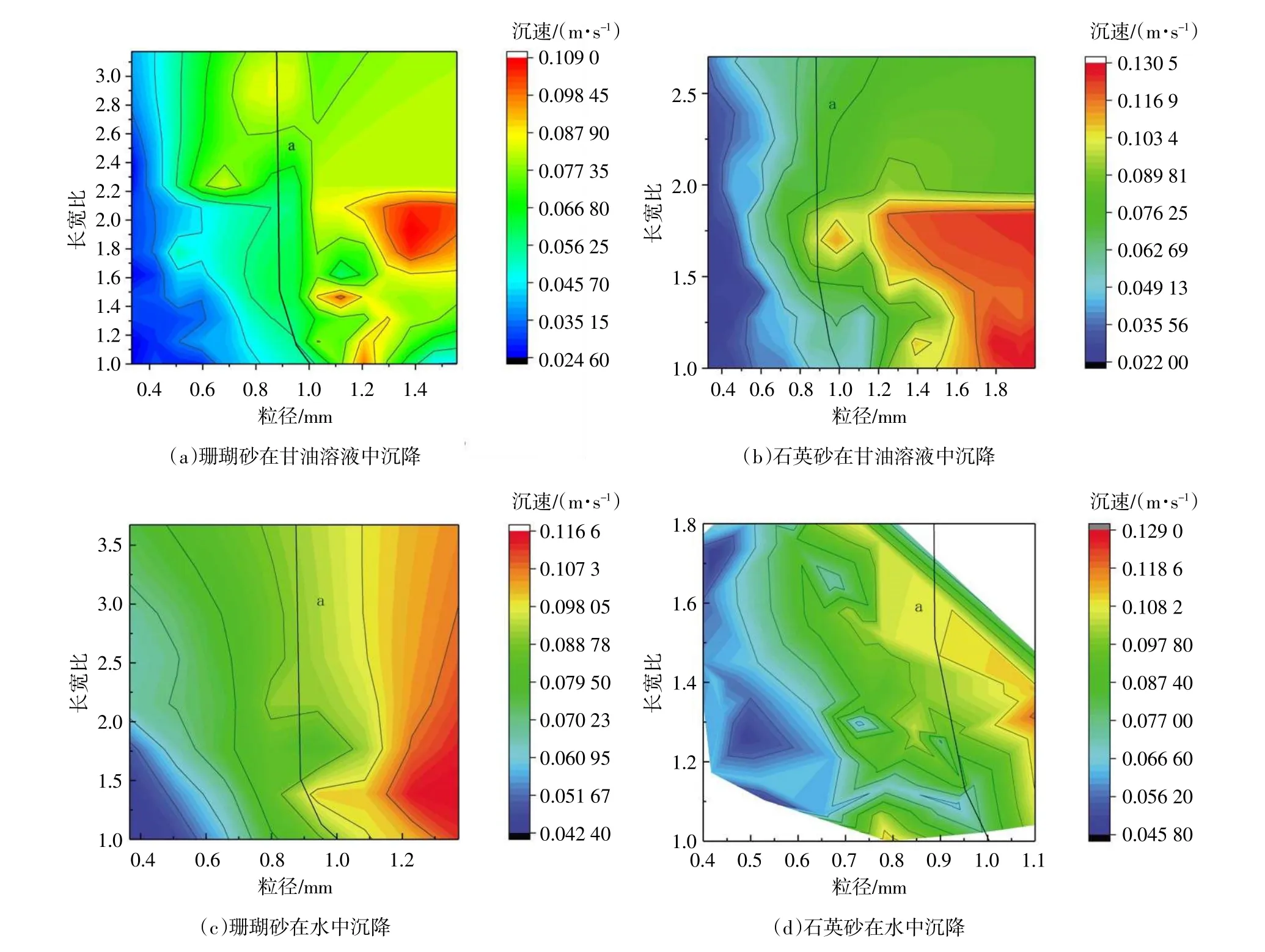
图4 两种砂在不同黏度流体中沉速与粒径、长宽比关系

3 分析与讨论

描述珊瑚砂的形状非常困难，但可以观察颗粒在沉速方面的表现，直接分析形状对沉降的影响。本文据此提出动力形状因子茁，具体推导如下。

3.1 动力形状因子推导

在沉降过程中，按照牛顿的绕流阻力公式，流体对运动的颗粒产生的阻力R 为：

式中：Cd为阻力系数，F 为物体垂直于运动方向的面积，酌w为流体比重，棕为颗粒的沉速，g 为重力加速度。

经过众多学者研究，Cd被判定为沙粒雷诺数Re 的函数。国内外普遍认同将水流状态分为三个区域，层流区、过渡区以及紊流区。通过Re 的数值对所在区域进行判断。Morsi 等（2006）推导了雷诺数与Cd之间更为细致的公式，为了对动力形状因子进行更精确的分析，在本文中对于Cd与Re之间的关系，选用Morsi 的研究成果（公式2）。

当研究对象为非球形时，颗粒受到的阻力R忆会因为形状与球形的差别而发生改变。沙玉清（1956）提出使用等效体积来表征球形的粒径，但考虑到颗粒的体积难以测量，使用等效体积法存在一定的困难，故使用等效粒径法，即认为球形的直径与颗粒的最短径相等，由于形状对沉速造成的影响体现在C忆d 中，此时下沉过程中颗粒受到的阻力如下式：

将公式（2）带入公式（5）中，即得到茁在不同雷诺数下的表达式。此时砂粒的最终沉速为：

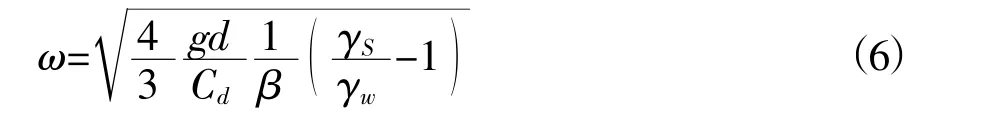
式中：酌杂为砂粒比重。

动力形状因子茁的物理意义为水流流经砂粒表面造成的阻力与水流流经相同粒径下球形表面造成的阻力之比，可以用于表征形状对沉降造成的影响。茁越大，说明形状对沉速的影响越大。通过比较珊瑚砂和石英砂茁值之间的差别，来定量研究形状对珊瑚砂和石英砂沉降产生影响的不同，进而对砂粒的沉速做出预测。茁=1 说明形状未产生影响，茁>1 说明形状起到了阻力作用，减缓了砂粒沉降速度，茁<1 说明形状加快了砂粒沉降速度。

本试验四种工况下计算的茁值如图5 所示。

图5 两种砂在不同黏度流体中粒径d 和动力形状因子茁的关系

3.2 颗粒沉速计算

沉降的应用包括已知粒径计算沉速或通过沉速估测粒径。接下来将通过推导的动力形状因子计算本试验中珊瑚砂和石英砂的沉速。

在已知粒径d（短轴径）的情况下，可以通过公式计算雷诺数Re，代入公式（2）中得到阻力系数Cd；通过表2 中动力形状因子茁的拟合函数得到其最大值和最小值；将粒径d（短轴径）、阻力系数Cd、茁最大值和最小值代入公式（6）中即可计算出颗粒的最终沉速范围（图6）。

表2 动力形状因子拟合结果

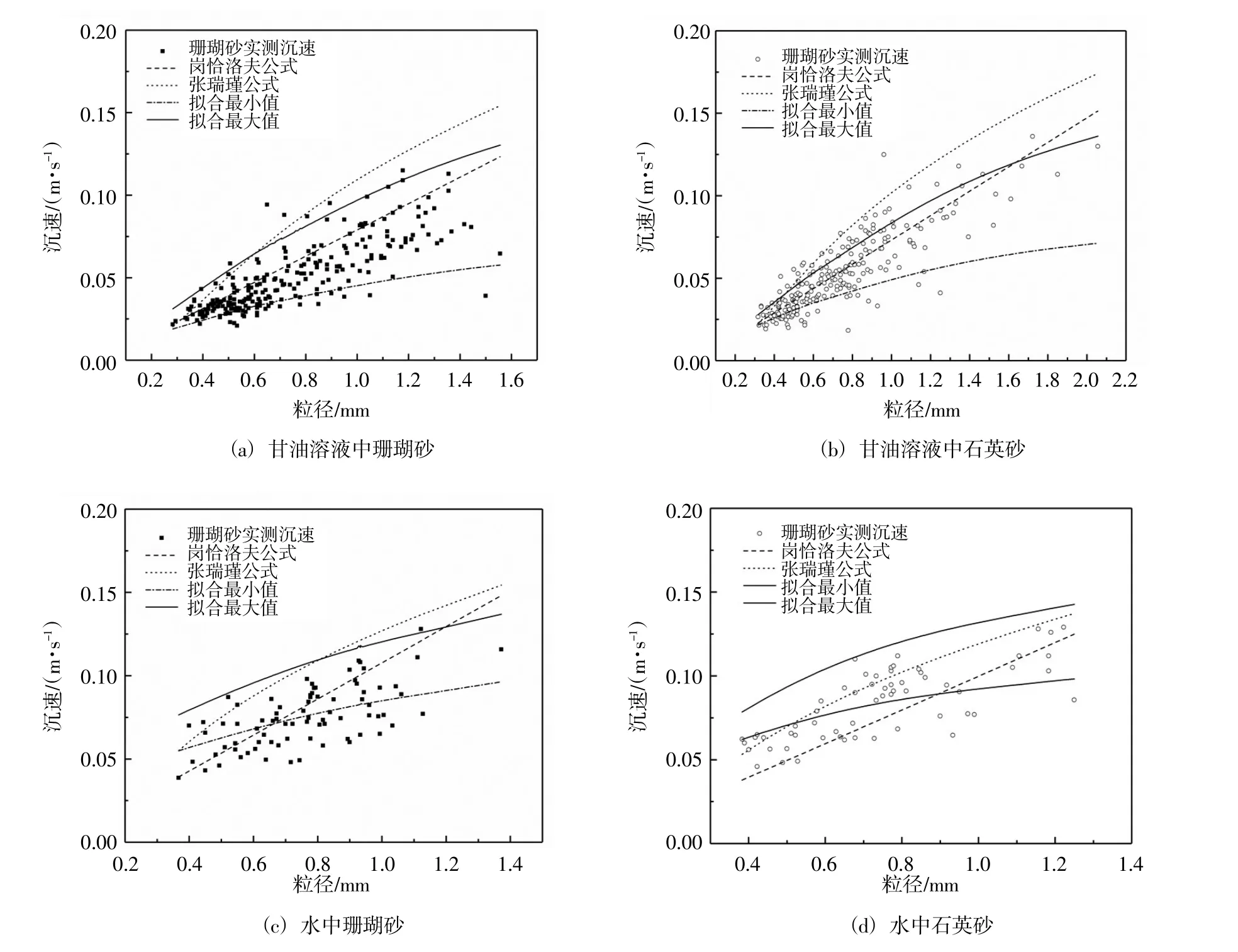
图6 沉速拟合结果

图中张瑞瑾公式能够准确地计算水中石英砂的沉速，对于水中珊瑚砂以及甘油中珊瑚砂和石英砂的沉速计算普遍偏大。冈恰洛夫公式能够对各条件下珊瑚砂和石英砂沉速进行较为准确的计算，但沉速的计算结果随着粒径的增大而逐渐出现偏大的现象。而本文的计算方法在高黏度下计算结果较为准确：将石英砂和珊瑚砂的沉速包含在一个扇形区间内。但在水中的计算结果却出现一些问题：所计算的沉速最大值结果较好，沉速最小值计算结果偏大。

考虑到流体对颗粒产生的阻力与垂直运动方向的面积有关，故该现象可能是由于在投放砂粒时角度不同所引起的。图7 显示了颗粒以最大投影面和最小投影面入水的运动过程。最大投影面沉降的颗粒以直线下降，沉速为0.066 m/s，而以最小投影面入水的颗粒处于打摆状态，由于流体黏度较小，其沉速在经过短时间加速阶段后并无增加现象，仍然保持打摆的运动状态，消耗了较多的能量，最终沉速为0.059 m/s。而在甘油溶液中，较低的沉速使不同入水角度影响不明显，由于黏度较大，颗粒能够较快地调整自身的沉降角度，脱离打摆的状态，最终沉速较为集中。在前人的研究中，颗粒的实际沉速棕0与计算得沉速棕之间的关系为棕0=a棕，a 一般可取平均值0.6（童祜嵩，1989）。

图7 不同角度投放砂粒的运动形态

图8 修正后计算最小值

4 结论

本文针对珊瑚砂和石英砂两种不同的砂粒，进行静水沉降试验，通过对试验数据的处理分析，得到以下结论：

（1）长宽比并不能很好地描述形状产生的影响，故提出动力形状因子这一无量纲参数。试验证明该参数能够较好地描述形状对沉降带来的影响。在不同黏度和粒径条件下，珊瑚砂的动力形状因子变化范围都大于石英砂。说明在沉降过程中珊瑚砂受到形状的影响要高于石英砂，具体影响程度受到粒径和黏度的影响。

（2）通过动力形状因子，提出考虑形状影响的砂粒沉降公式，通过计算同一粒径颗粒沉速的最大值和最小值，整合所有粒径后包围出一个扇形区域，在本试验条件下的大部分试验沉速都落在扇形区域内，能够较好地描述颗粒沉降的范围，且计算的准确度随着黏度的增大而增大。在水中能够准确地描述颗粒沉降的最大值，最小值由于颗粒入水角度问题会出现误差，可以考虑使用经验系数进行修正。

致谢：中国海洋大学环境科学与工程学院程子睿和魏莉莉对试验提供了帮助，任宇鹏对论文修改提供了帮助，在此一并致谢。