能处理一类“why 问题”的问题逻辑系统

2021-10-20张保垒

逻辑学研究 2021年4期

张保垒

1 问题逻辑的基本概念

问题逻辑（the logic of questions 或erotetic1英文单词erotetic 源于希腊文单词erotema，后者的意思是“问题”。（参见[6]，第1 页）logic）是逻辑学的一个分支，又称为问句逻辑（the logic of interrogatives 或the logic of questions）、问答逻辑（the logic of questions and answers）、询问逻辑（interrogative logic）等，它主要研究与问题有关的话题，诸如：问句（interrogatives 或questions）及问句所表达问题（questions或issues）的逻辑结构，问题与解答（answers）的关系，问句的语义解释，适用于问题的推理关系，互动场景中提问（questioning）或问答行为对信息流的影响，问句的预设，语用及有关的哲学话题等。

汉语中的“问题”又称作“问句”，与英文中的“interrogatives”或“questions”意思相近。“问句”属于一种句子类型，存在于自然语言或形式语言中，“问题”的所属则不那么明显：有时它指一种特殊类型的句子，如“各种自然语言中的问题都有一些独特的语法特征”；有时还可以指称一种思维形式，如“我们提出问题时经常借助疑问句”。英语中“questions”一词的常见含义有三种：自然语言或形式语言中的问句（interrogatives）、作为行为方式的提问（questioning）和作为语义内容的问题（issues）。2对question 一词的详细讨论，参见[2]，第1059 页。研究“questions”的不同学科尤其是问题逻辑中的不同进路都有各自所关注的某种含义，举例而言：语言学尤其是其语法部分主要研究第一种含义下的“questions”，语用学特别是言语行为理论主要研究第二种含义，第三种用法下问题的含义（sense），或提问行为的内容（content）则是问题逻辑尤其是其逻辑语义部分的关注对象。

与问题有关的诸多概念中，最重要的一个可能就是“解答”（answers），作为语言形式的“问题”（即问句），其解答也是某种语言形式，作为问句之语义内容的“问题”，其解答也是一个语义概念。问题逻辑研究中往往对解答做两点规定：（[1]，第3 页）

(i) 问句的解答是陈述句，相应地，作为语义形式的问题，其解答是命题。

(ii) 解答所提供的信息，不多不少恰好是解决问题所需要的信息，即解答应当“完全地、且恰好完全地解决了问题”。

问题的预设也是问题逻辑研究中的一个重要概念，在“预设”一词的直观用法下，无论在语义还是语用层面上，一个问题都预设了很多东西，问题逻辑中研究的预设主要是一个语义概念，在语义层面，所有的逻辑规律都是任一问题的预设，但研究者希望在一个更狭窄的意义上谈论问题的预设，其中贝尔纳普对问题预设的定义被问题逻辑研究者普遍接受：“一个陈述是一个问题的预设，当且仅当该陈述的真是该问题有真解答的必要条件。”（[1]，第5 页）在某问题的诸多预设中，可能有一些预设能衍推其他所有预设，这类预设在语义上对应同一个命题，在语法上往往能定义出表征该命题的一个公式，这一公式常被称作问题的唯一预设（the presupposition），本文使用“预设”一词，多是在“唯一预设”的意义上使用。

2 “whether 问题”和“why 问题”

可将中的问题分为两类，即：

（中的）“whether 问题”，指形如?{A1,...,An}（其中n ≥2 且A1,...,An都是经典公式且互不相同）的表达式。whether 问题?{A1,...,An}可读作“诸命题A1,...,An中哪个成立？”，形式的whether 问题一般用于表征自然语言中具有有限个解答的问题，后者被称作自然语言中的whether 问题，如“Whether he is coming?”、“Who is coming,Ann or Bob?”、“今天是星期几？”等。有一类特殊的whether 问题，即形如?{A,～A}的问题，称作是非问题，其直观含义是“A成立与否？”。本文规定，whether 问题?{A1,...,An}的所有解答构成的解答集即{A1,...,An}3注意，{A1,...,An}是一个集合，但问题表达式?{A1,...,An}中的“{ }”不是集合符号，而是逻辑常量符号。，预设是A1∨...∨An。

（中的）“why 问题”，指形如?{A}的表达式，其中A是经典公式。本文规定，why 问题?{A}预设即公式A，其解答是形如B1,...,Bn,((B1∧...∧Bn)→A)（其中n ≥1 且B1∧...∧Bn不同于A）的任一公式序列，这种why 问题所表征的只是自然语言中的一类why 问题，即询问某个命题成立的原因、理由或充分条件的why 问题，例如问题“为什么电灯灭了？”及其一个解答“停电了，停电就导致电灯灭”可分别表征为?{A}和B,B →A（其中A表示“电灯灭了。”，B表示“停电了。”），再如“为什么桌面受到的空气压力增大了？”及其一个解答“空气压强增大了，桌面受力面积没变，前两者导致桌面所受压力增大。”可分别表征为?{A}和B1,B2,(B1∧B2→A)（其中A表示“桌面受到的空气压力增大了。”，B1表示“空气压强增大了。”，B2表示“桌面受力面积没变。”）。

Why 问题具有重要研究价值，科学哲学中对某个事实F的解释可理解为对关于这一事实的why 问题“WhyF?”的回答，因而对why 问题的逻辑分析对于科学解释而言是一项重要工作，历史上很多科学哲学家都对why 问题有过讨论。（[5]）Why 问题也具有特殊性，其本身及其解答的逻辑结构似乎比其他问题更为复杂，本文无意解决与why 问题有关的种种困难，仅关注形式语言中的上述那类why 问题并构建一种相应的逻辑系统，这种构建是在辛迪卡的有关工作基础上进行的，接下来先对辛迪卡的询问探究模型进行简要考察。

3 辛迪卡的询问探究模型IMI

辛迪卡的询问探究模型IMI在不同语境中含义可能不同，它有时指一种特定的思想范式，这种范式在探究者的推演行为之外特别强调提问行为在探究过程中的作用，这种用法下的IMI是一个专有名词，即the interrogative model of inquiry，作为思想范式的IMI被辛迪卡描述为一种博弈活动，即探究者（the Inquirer）和自然界（Nature）在某个固定模型基础上的博弈，探究者的目标是获得某个特定结论或解决某个特定问题，为实现目标可采取提问行为或推演行为：借助提问，探究者向自然界获取信息并将其用于后续探究，借助推演，探究者在已有信息的基础上进行普通的演绎推理。自然界在这一活动中就像一个配角，其作用只是回答探究者的提问：在可以回答的时候给出回答。辛迪卡之所以用博弈论的术语表达IMI的思想，只是为了强调探究活动中的策略因素，IMI的具体版本很少用到现代博弈论的结果。若要在技术上实现上述想法，就要构建IMI的具体版本，诸如经典命题逻辑版本、一阶逻辑版本、认知逻辑版本等，抽象意义上IMI中的推演行为和提问行为在具体版本中分别实现为演绎步骤（deductive moves）和询问步骤（interrogative moves），两类步骤在具体逻辑系统内的实施则要借助各种逻辑规则。后文中IMI所处的语境将表明该词是在哪种含义下被使用的。

辛迪卡在构建IMI的形式系统时，采用的是以贯列（sequents）为结点的表列演算（tableau calculus）样式，一般含有四类规则：结构规则、联结词规则、特殊规则和提问规则，其中提问规则说的是：“若某问题的预设出现在了子表列的左侧，探究者就可以向信息库（the oracle）提出该问题，若信息库做了解答，就将解答添加到子表列左侧。”（[3]，第51 页）4辛迪卡只给出了提问规则的自然语言表述，且这种表述适用于IMI 的一系列版本。结构规则、联结词规则、特殊规则随着IMI 具体版本的不同而有所区别，一阶版本IMI 中的这三类规则参见[3]，第48–53 页。提问规则表明，IMI中的推导是探究者与信息库之间互动的结果，其中信息库的唯一贡献是回答探究者提出的问题，推导的主角是探究者，探究者在推导过程中既可运用前三类规则从某个贯列得出一个新贯列，这类步骤类似于经典演绎推理，称作演绎步骤，探究者还可以从某个贯列基础上依据提问规则提出问题，并将信息库的回答纳入推导序列中，这种步骤称作询问步骤，正因为允许询问步骤，IMI系统中的推导才被称作询问推导（interrogative derivation）。

辛迪卡在分析IMI的形式系统时特别强调认知因素，比如着力构建认知版本的IMI系统，而针对非认知版本的IMI系统，则认为其中的每个经典公式A 都有一个隐藏的前缀认知算子K（[3]，第190–191 页），这样一来，就可以用与问题求解有关的术语来描述询问推导，以一阶版本IMI为例，设其中某推导序列的初始贯列是T ⊢C（其中T是一个公式序列，C是一个公式），认知视角下贯列结论C被看作某个问题Q的所需（因为C之前被认为有隐藏的认知算子），由贯列结论开始的询问推导过程即对问题Q的求解过程，故Q被称作该询问推导的首要问题（the principal question），在询问推导过程中，还有可能产生一些向信息库提出的问题，这些问题称作操作问题（operative questions），首要问题和操作问题之分对辛迪卡使用IMI分析why 问题尤为重要。

辛迪卡对why 问题的分析是非常独特的，这种分析需要从认知角度进行，在的任一经典公式前均增加一个认知算子后，可将辛迪卡对whether 问题和why问题的分析总结如下：whether 问题的预设、解答集、所需的逻辑形式分别是K(A1∨...∨An)、{KA1,...,KAn}、KA1∨...∨KAn，其中“问题的所需（the desideratum of a question）”，被定义为“提问者通过正常使用问题想要达到的特定认知状态”。（[4]，第25 页）5定义中的“正常使用”指提问者确实不知道问题的正确解答并想通过提问改变这种无知状态，这就排除了对问题的某些使用方式，包括教师用她们已知道答案的问题去测验学生，及对问题的修辞性用法等。辛迪卡认为，why 问题是whether 问题退化为n=1 时的情形，故why问题的形式是?{A1}，这种退化不仅体现在why 问题的逻辑形式，还体现在其所需、预设、解答：whether 问题?{A1,...,An}的所需、预设、解答当n=1 时均为KA1，从而why 问题?{A1}的预设、所需、解答的形式也都是KA1，基于这种分析，辛迪卡声称why 问题不像很多研究者所认为的是一类逻辑结构复杂的问题，而是一类逻辑上极为简单的问题。然而，辛迪卡的这种解读方式偏离了对why 问题的传统认识和直观理解，与自然语言中why 问题的实际使用情况相去甚远。在自然语言中，人们询问“Why A?”（?{A}），更多地是追问A之所以成立的原因、理由或充分条件，将这些原因、理由或充分条件作为解答是合理的，而辛迪卡用“知道A”（KA）来解答则令人费解，并不适当。本文采用对why 问题的传统认识和直观理解，结合自然语言的实际使用情况，构建一个能处理这一类why 问题的新系统。

4 能处理一类“why 问题”的问题逻辑系统IMIpw

本节构建问题逻辑系统IMIpw，它不仅能处理whether 问题，也能处理上述那类why 问题。IMIpw的形式语言即语言，IMIpw中的变形规则都是针对贯列的，贯列的定义如下：6本定义参考了[7]，第3 页的定义1.1.4。

定义2(IMIpw中的贯列).IMIpw中的贯列指形如A1,...,An ⊢B1,...,Bk的表达式，其中：n ≥0，n ∈N（N 是全体自然数的集合），k ≥0，k ∈N，Ai ∈（1≤i ≤n），Bj ∈（1≤j ≤k）。推断符号“⊢”左侧的公式序列A1,...,An称作该贯列的贯列前提（the antecedent），“⊢”右侧的公式序列B1,...,Bk称作该贯列的贯列结论（the succedent 或the consequent）。

当贯列前提或贯列结论为空时，相应地在“⊢”的左侧或右侧不写任何记号，如“⊢B1,...,Bk”、“A1,...,An ⊢”、“⊢”都是贯列。“A1,...,An ⊢B1,...,Bk”的直观含义是：“（在系统IMIpw中）以序列A1,...,An为前提可推出序列B1,...,Bk”，改用语义术语即：“若A1,...,An ⊢B1,...,Bk的前提中每一个公式为真，则该贯列的结论中至少一个公式为真”，从而贯列前提中的逗号被看作合取，贯列结论中的逗号被看作析取。本章用α、β（均可加下标）表示任意的贯列，用Γ、∆（均可加下标）表示任意的有限的经典公式序列（可以没有公式）。

系统IMIpw是在语言的基础上，添加结构规则、联结词规则、特殊规则和提问规则构成的。IMIpw采用表列演算的样式来进行推理，其中前三类规则（即结构规则、联结词规则和特殊规则）的直观含义如下：规则的含义是：“若贯列α表示的推断不成立，则贯列β表示的推断也不成立”，规则的含义是：“若贯列α表示的推断不成立，则贯列β1 或β2 表示的推断至少有一个不成立”。“贯列α表示的推断不成立”的含义是：“有可能α的贯列前提都为真且α的贯列结论都为假”。

下面分类列出IMIpw中的变形规则：

1.结构规则分为弱化（weakening）规则、收缩（contraction）规则、交换（per mutation）规则7系统IMIpw 的贯列中，贯列前提和贯列结论都可能含有多个公式，所以每个结构规则分为左右两类：LW（左弱化）、LC（左收缩）、LP（左交换）、RW（右弱化）、RC（右收缩）、RP（右交换）。：

(LW)的直观含义是：由较多前提推不出的东西，由较少前提也推不出；

(RW)的直观含义是：由特定前提若推不出较多可能性中的一个，则也推不出较少可能性中的一个；

两条收缩规则表明，同一公式出现多次和出现一次的效果相同；

交换规则表明，两个公式在序列中的先后位置无关紧要。

2.联结词规则8关于析取和合取的规则参考了[3]，第49 页，关于否定的规则出自[8]，第490 页。

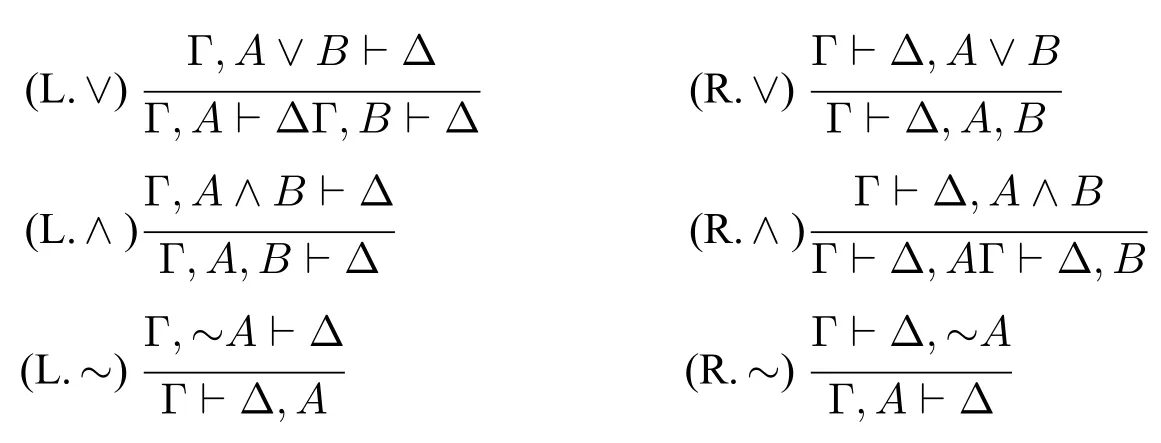
前两类规则构成了经典命题逻辑的一种表列演算系统。

3.特殊规则9辛迪卡构建的IMI 系统中仅将这条规则与规则(R.cont)单独列出，系统IMI 中没有称它们为特殊规则，参见[3]，第52–53 页，系统IMIpw 中用不到规则(R.cont)。

本规则在经典命题逻辑中亦成立。对于IMIpw中的询问步骤而言，此规则必不可少，故将其归类为特殊规则。10该规则在本文的系统IMIpw 的地位与其在辛迪卡的某些IMI 系统中相同，所以在此不再详细讨论，可参见[3]，第40–42 页。

4.提问规则提问规则涉及一个关键概念，即信息库，信息库在探究活动中的角色是配角：仅对探究者的提问做回答。辛迪卡的IMI中一般假定信息库满足四个条件，即：11前三条参见[3]，第48 页，第(iv)条是本文加上的。

(i) 一场探究活动只有一个信息库；

(ii) 信息库所提供的解答集在探究过程中保持不变；

(iii) 信息库所提供的解答都为真，且探究者知道其为真；

(iv) 当某问题有解答在信息库中时，信息库一定要回答该问题。

IMIpw中的信息库也满足上述四点要求，为叙述方便，设IMIpw中信息库能给出的回答构成集合OP，OP是一个由中的经典公式构成的一致集（它可能是无限的，也可能是空集）12即无矛盾的集合，亦即有经典模型的集合。，称其为IMIpw中信息库的解答集（the set of all answers of the oracle），在不致混淆时简称其为（IMIpw的）信息库。在IMIpw中，探究者一定知道信息库的存在，从而在某些情形下会求助于信息库，但探究者预先却不知道信息库解答集的外延（所以有可能信息库无法回答任何问题，但探究者还是会向其提问），正因为如此，询问行为才可能会扩展探究者的知识，询问探究模型中探究者所作的推理才不仅仅是演绎推理。在IMIpw中，探究者既可向信息库提出中的whether 问题，也能提出中的why 问题，所以IMIpw中有两条提问规则，分别表述如下：

whether 提问规则(L.Qwhe)：推导过程中，若whether 问题?{A1,...,An}的预设即A1∨...∨An是某贯列Γ⊢∆的一个前提公式，则探究者可以向信息库提出问题?{A1,...,An}。若信息库给出了回答Ai（1≤i ≤n），则可得出贯列Γ,Ai ⊢∆。

规则(L.Qwhe)的图示是：其中Ai（∈OP）是信息库对问题?{A1,...,An}的回答。

设α=Γ1,A1∨...∨An,Γ2⊢∆，而β=Γ1,A1∨...∨An,Γ2,Ai ⊢∆，规则(L.Qwhe)的直观含义是：在信息库的解答集OP中的元素都为真的前提下，若贯列α表示的推断不成立，则贯列β表示的推断也不成立。

why 提问规则(L.Qwhy)：对于贯列Γ,A ⊢∆，探究者可以向信息库提出why问题?{A}。若信息库给出回答B1,...,Bn,((B1∧...∧Bn)→A)（其中n ≥1 且B1∧...∧Bn不同于A），则探究者可得出贯列Γ,B1,...,Bn,((B1∧...∧Bn)→A)⊢∆。

规则(L.Qwhy)的图示是：其中公式序列B1,...,Bn,((B1∧...∧Bn)→A)（其中每一公式均是OP中的元素且B1∧...∧Bn不同于A）是信息库对why 问题?{A}的回答。

规则(L.Qwhy)的直观含义与规则(L.Qwhe)的直观含义类似，亦即在信息库的解答集OP中的元素都为真的前提下，若规则(L.Qwhy)前提中贯列表示的推断不成立，则结论中贯列表示的推断也不成立。

IMIpw中的推导是一种询问推导，其中不仅允许结构规则、联结词规则和特殊规则所导致的演绎步骤，还允许提问规则所导致的询问步骤，IMIpw中对贯列Γ⊢∆的询问推导可表示为向下生长的树型表列，相关定义如下：

定义3(表列及其分枝13该定义中的有关术语参考了[7]，第5–6 页中的定义1.1.6。).

(i) 由单个贯列“Γ⊢∆”构成的图示称为“一个以Γ⊢∆为根的表列”，这个表列也是其自身唯一的分枝。

(ii) 由贯列“Γ⊢∆”出发，运用IMIpw中的变形规则（结构规则、联结词规则、特殊规则或提问规则）构造的任一推导图示，均是“一个以Γ⊢∆为根的表列”或称“Γ⊢∆的一个表列”或“Γ⊢∆的一个推导”。设贯列序列α1(=Γ⊢∆),α2,...,αn（n ≥2）出现在以Γ⊢∆为根的某个表列T 中，其中每个αi+1（i=1,2,...,n −1）都是由上一个贯列依据IMIpw中的变形规则得到的，且αn的下方没有其他公式，亦即不对αn施加变形规则，则称贯列序列α1(=Γ⊢∆),α2,...,αn（n ≥2）是表列T 的一个分枝，并称任一αi（1≤i ≤n）为该分枝的一个结点。

(iii) 设T 是Γ⊢∆的一个表列，则Γ⊢∆的贯列前提中的公式亦称作T 的初始前提（the initial premise），T 的所有初始前提组成的集合称作T 的初始前提集，Γ⊢∆的贯列结论中的公式亦称作T 的最终结论（the ultimate conclusion）。

Γ⊢∆表示的推理是否成立，将根据能否构造出Γ⊢∆的一个封闭表列来判定，接下去给出封闭表列的定义：14该定义方式参考的是[3]，第50 页。

定义4(封闭表列).一个表列是封闭的，当且仅当该表列的所有分枝是封闭的。其中，表列的一个分枝是封闭的，当且仅当其某个结点为以下三种贯列之一：

(i) 同一公式及其否定均是该结点的贯列前提；

(ii) 同一公式及其否定均是该结点的贯列结论；

(iii) 同一公式既是该结点的贯列前提又是其贯列结论。

如果在表列构造过程中，一个分枝在某个结点实现封闭后，就不再对此结点施加变形规则，换言之，已经封闭的分枝将停止生长，因为上述三种情形都意味着矛盾的出现，前文已指出对IMIpw变形规则中的贯列要按其不成立理解，即“有可能贯列前提都真且贯列结论都假”，情形(i)中，贯列前提不可能都真，情形(ii)中，贯列结论不可能都假，情形(iii)中，贯列前提都真则意味着贯列结论中至少有一个公式为真，三种情形都与该贯列的不成立相矛盾。从而若Γ⊢∆的某个表列的任意分枝都封闭，就意味着Γ⊢∆不成立会导致矛盾，故在系统IMIpw中，Γ⊢∆的一个封闭表列T 就是对Γ⊢∆的一个证明，若IMIpw中存在Γ⊢∆的一个证明，则意味着从Γ 到∆的推导是成立的，这种推导概念的形式定义是：

定义5(IMIpw中的推导).设T={A1,...,An}（n ≥0）是一个由经典公式构成的公式集，C是一个经典公式，M是使得OP中所有元素为真的一个经典模型（即一个经典赋值）。则称“C是在模型M中基于初始前提集T经询问推导得出的”（记作：M:），当且仅当，在IMIpw中能构造出贯列A1,...,An ⊢C的一个封闭表列。并称T 是该询问推导的初始前提集，C是该询问推导的最终结论（ultimate conclusion）。

根据上述定义，IMIpw中的询问推导与辛迪卡的IMI中的询问推导类似，也是一个混合概念，是传统真概念和逻辑后承概念的集成：

(i) 若推导过程中没有提出任何问题，则这种推导是从T到C的经典推导，即贯列A1,...,An ⊢C的封闭表列中未使用提问规则；

(ii) 若T为空集且推导过程中提出的问题（可以没有问题）都得到了解答，这种情形下的询问推导得出了C在M中的真，记作M |=C；

(iii) 若推导的初始前提T非空，且推导过程中用到了信息库给出的解答（即使用了提问规则），则称这种询问推导的最终结论C是借助信息库从前提集T得出的。

下面是IMIpw中的几个推导实例：

例1.

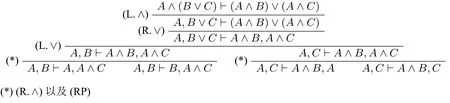
该例没有用到提问规则，从而这种询问推导实质上是经典的演绎推导。

例2.设初始前提集T为空集∅，下面是询问推导M:p ∨q的一个封闭表列，它用到了规则(L.taut)和规则(L.Qwhe)：

(*)根据(L.Qwhe)提出?{q,～q}，并得到回答q。

其中在第二行借助(L.taut) 引入了重言式q ∨～q，这意味着可以提出问题?{q,～q}，第三行中借助(L.Qwhe)得到了解答q，这意味着q ∈OP。这种情形下询问推导的最终结论是靠提问得出的，于是有：M |=q。

下面是一个既用到规则(L.Qwhe)又用到规则(L.Qwhy)的例子：

例3.设A和C ∧D均不同于B，以下是询问推导M:～(～C ∧D)的一个封闭表列：

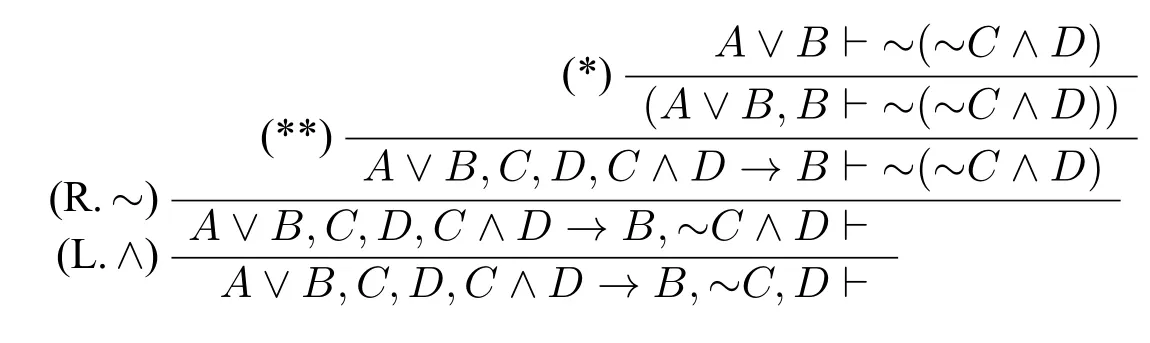
(*) 根据(L.Qwhe)提出?{A,B}并得到回答B

(**) 根据(L.Qwhy)提出?{B}并得到回答C、D和C ∧D →B

在上述表列的的询问步骤中，信息库对whether 问题?{A,B}的回答是B，信息库对why 问题?{B}的回答是C、D和C∧D →B，由此可知，{B,C,D,C∧D →B}⊆OP，于是B、C、D和C ∧D →B都在模型M下为真。

接下去证明几个元定理。IMIpw推导过程中，问题的解答可以作为进一步推演的前提，从而由前提集T出发的询问推导与以OP ∪T为前提的经典演绎推导有某种联系，下面的元定理就反映了这种联系：15该定理的证明参考了辛迪卡对一阶版本IMI 系统的完全性定理的证明，参见[3]，第53–54 页。

定理1(询问推导与经典推导的关系定理).设T={A1,...,An}（n ≥0）为初始前提集，OP为IMIpw中信息库的解答集，M是OP的一个经典模型，则：结论C是在M中基于初始前提集T经过询问推导得出的（即M:C）当且仅当C是可由OP ∪T通过经典演绎推导得出的，即OP ∪T ⊢C。16注意符号“⊢”的三种出现方式：“⊢”的左右两边均是公式序列时，Γ ⊢Δ 表示一个贯列；“⊢”的左边是公式集T，右边是单个公式C 时，T ⊢C 表示存在从T 到C 的经典演绎推导；M :C 则表示系统IMIpw中存在从T 到C 的询问推导。

证明.先证从左到右。设M:C，则此时IMIpw中存在贯列A1,...,An ⊢C的封闭表列T，可对T 分两种情形讨论：

• 情形一，T 中没有使用提问规则，此时T 可直接作为从T到C的一个经典演绎推导，于是有T ⊢C，再根据经典演绎推导的单调性，即得OP ∪T ⊢C。

• 情形二，T 中使用了提问规则(L.Qwhe)或(L.Qwhy)，且整个过程中借助提问规则得到的解答依次是S1,...,Sn，则这一询问推导可转换为一个经典演绎推导{S1,...,Sn}∪T ⊢C：只需删除原询问推导表列中由提问规则得到的贯列并将S1,...,Sn添加到其余的每个贯列的前提中即可。例如，前述例3中的询问推导M:A ∨B～(～C ∧D)中有两次提问，分别得到解答B和C、D、C ∧D →B，删除两个提问规则得到的贯列，并将B，C，D，C ∧D →B添加到其余的每个贯列的前提中，则该询问推导就可转换为经典演绎推导{A ∨B,B,C,D,C ∧D →B}⊢～(～C ∧D)，推导表列如下：

而{S1,...,Sn}⊆OP，根据单调性，即得OP ∪T ⊢C。

再证从右到左。设OP∪T ⊢C，且该演绎推导中用到OP中的元素有S1,...,Sn，则在经典命题逻辑中存在贯列A1,...,An,S1,...,Sn ⊢C的一个封闭表列，这一表列可按下述思路以转换为系统IMIpw中贯列A1,...,An ⊢C的一个询问推导表列：从A1,...,An ⊢C出发，对i=1,...,n，依次使用规则(L.taut)引入Si ∨～Si，再根据提问规则(L.Qwhe)对问题?{Si,～Si}做解答Si。此后再根据弱化规则(LW)删除每个Si ∨～Si并拼接上贯列A1,...,An,S1,...,Sn ⊢C的上述表列即可。例如，设T={A}，{B}⊆OP，C=A ∧B，则有OP ∪A ⊢A ∧B，因为有以下的封闭表列：