如何让通用人工智能系统能够“识数”
2021-10-19徐英瑾
徐英瑾

摘 要: “识数”的字面意思就是说,数字表达式的使用者需要知道这些表达式日常实践中的具体意义,如知道“十公里”算不算“路远”,“十万元”算不算“昂贵”。主流人工智能系统虽然都是数码化的,但却未必真正“识数”,因为它们都无法以一种灵活的方式来理解数字表达式在特定的日常语境中究竟意味着什么,并在这种理解的基础上进行复杂的语用推理。为了使得人工智能系统能够“识数”,工作思路应是在非公理化推时系统的平台上来构建数字表征。训练非公理化推理系统使之“识数”的指导原则,就是先教会它表征那些最不抽象的数学概念,再一步步进展到更抽象的概念。而这一教学步骤的安排,与我们教导儿童识数的路线图是有点相似的。在这个面向机器的数字教学法中,我们将以对“逻辑专名”的教学作为对数字表征教学的重要前导。
关键词: 数感;知觉;通用人工智能;非公理化推理系统;逻辑专名
中图分类号:TP18 文献标识码:A 文章编号:1004-8634(2021)05-0024-(13)
DOI:10.13852/J.CNKI.JSHNU.2021.05.003
一、导言:什么叫“识数”
在人类的知识中,大量的内容都包含了数字表征。例如,在经典的盖梯尔问题中,对于“史密斯知道得到工作的那个人口袋里有十枚硬币”这样的命题,1 就包含了“十枚硬币”这样包含数字的表征。然而,这样的命题所涉及的数字表征(如“十……”)是如何与那些非数字表征(如“……枚硬币”)结合在一起的呢?对于这个问题,西方主流知识论学界并没有投入大量的资源来加以研究。在本文中,笔者将试图从人工智能哲学的角度,阐明通用人工智能系统获得与日常生活相关的数学知识的原理,从而为我们进一步理解数字表征在日常知识中的地位提供一个新的视角。
初看起来,由于我们已经假定了所有的人工智能系统都是数码化的,所以,“人工智能究竟该如何表征数字”这个问题似乎就根本没有被加以单独讨论的必要了。但是,我们这里说的“数字表征”的真正含义却是“识数”,也就是把握一个带有特定单位的数字表征的具体实践意义,比如,知道“十公里”算不算“路远”,“十万元”算不算“昂贵”。这种意义上的“识数”,也可以被理解为对于“数感”(number sense)的把握。 “数感”一词由心理学家丹齐格(Tobias Danzig)首创,2其字面意思就是:数字的使用者在他们的日常实践中对数字的实践意义的领会。根据戴夫林(Keith Devlin)的理论,1数感的获取有赖于两种能力的预先获得:第一,估数(subitizing),亦即比较那些通常在视觉中同时呈现的两批事物的数量的能力;第二,计数 (counting),即通过数数来回忆在时间中相继呈现的对象的数量的能力。而现有的人工智能系统,是否能够在上述意义上“识数”,则颇为成疑。
数感和符号运算之间的关系很复杂。一方面,基于如下两个理由,两者的确彼此不同:第一,数感只能保证主体具有估算数值的能力,而不是处理复杂与精密的符号运算的能力。第二,通常认为,数感的出现有赖于自然演化的历程,因为人类的数感和其他物种如鸟类、2鼠、3狮子4和黑猩猩5的数感具有相同的特征。与之相对比,进行符号运算的能力则毫无疑问与文化有关,因为在动物界中只有人类具有文化,并且只有人类会进行复杂的符号运算。
不过,另一方面,我们也有理由宣称数感和符号运算彼此是有紧密联系的。具体而言,符号运算的能力虽必然由特定文化所滋养,但同时也被人类的基因禀赋所限制,而这些限制的存在,则可以通过下面的例子来加以说明:在不同的文化中,人类均对十进制系统具有特殊的偏爱,而这一点,恰恰与“凡人均有十根手指”这一生物学事实颇有关联。6从这个角度看,与人类的生物禀赋更有关联的数感,其实是为各种文化中的各类数学构造提供了“原材料”——从这个角度看,没有哪类需要计算活动的人类文化的形成是离得开数感的。
上述这些描述必然是基于心理学或者生物学材料的。然而,为何人工智能需要关注这些材料呢?换言之,为什么人工智能系统需要数感?此外,在人工智能系统中实现对于数感的把握机制到底难不难?若是困难,其难点又何在呢?
二、为什么通用人工智能系统需要“识数”
首先,让我们不妨将在人工智能中与人类数感所对应的东西称作“人工数感”。它将从以下两个方面对人工智能提供重大贡献:
其一,“人工数感”会让人工智能体有能力在日常对话中进行适当的数量推理。例如,聊天机器人很有可能与人类一起讨论商品价格等物的数量。若要胜任此类谈话,人工智能体就应能将数字与非数字表征的评价词汇(“很多”“很少”“几乎足够”“太多”“太贵”等)联系起来,如整合为如下判断:“这幢别墅作价五百万美元,这实在太贵了”“让他捐三十元,对他而言已经算很多了”等。显然,判断者要做出这种判断,就必须依据不同的语境给出不同的“数词—评价词”配对模式。由此看来,人工智能体若无恰当的数感(不知道数字在日常实践活动中的意义),就根本无从打通数字、评价词、语境之间的推理通路。
其二,“人工数感”会提升人工智能系统做出数学创新的潜力。笔者所说的“数学创新”是指发现全新的数学知识,而不是再次“发现”已经发现过的东西。从康德7 到布劳威尔,8 在关于数学知识获取方式的认识论研究传统中,一直有学者认为数学创新和数学直觉有关。换言之,在数学中新构造出来的对象,必须能在某些可被直观的心理图像中获取其意义。这种主张也被称为“数学直觉主义”。虽然作为一种关于数学知识合法性的证成性理论(亦即关于数学创新应当是怎样的理论),数学直觉主义的合理性还未得到普遍赞同,但若我们仅仅将其视为一个心理学理论(亦即关于数学创新实际上是怎样的理论),该学说的学术价值则较少有争议。实际上,戴夫林1提到的两种与“数感”相关的能力——估数和计数——也是与数学直觉相关的,因此,此二者分别依赖于空间性的直觉和时间性的直覺。
不过,“直觉”这个术语依然带有人类中心主义的倾向。现在笔者就将它外推到人工智能体上。如何进行这种外推呢?笔者建议把“直觉”变为一个副词,即“在直觉上”。对于任何智能体而言,凡是能够与其可提取的记忆模式(不只是数学模式)构成类比的事项,都可以被说成是“在直觉上”存在的事项。照此,当我们说“A在直觉上是B”的时候,就相当于说“A是B”这一判断成立的情形,与系统的可提取记忆中的某个例子构成了类比关系。至于为何这种意义上的对于“在直觉上”的定义既适用于人类也适用于机器,乃是因为:这个定义中的关键短语(如“类比”“模式”“可提取的记忆”)无论对人类还是人工智能体都是适用的。依此思路,如果人工智能体要通过它所具备的数感或直觉来进行数学创新,它就应该把新的构造视为其经验中可提取模式的类比物,从而保证这些数学构造是富有意义的。
有人或许会问:人工智能体为何一定需要恰当的数学直觉来辅助数学创新呢?这是因为,倘若没有数学直觉的辅助,数学探索的效率将会降低。因为正确的数学直觉可以大幅度缩小数学探索的范围。换句话说,如果被构造的数学对象E与经验中常见的某种成熟的模式构成类比关系,那么,E看起来会比其他备选的有待构造的对象更有希望被构造成功。
不过,目前为止我们仅仅初步勾勒了一些大框架,来讨论如何在通用人工智能系统中实现自主的数学创新,关于这个话题,尚有更多细节方面的空白有待未来的研究加以充实。但是值得注意的是,在通用人工智能系统中实现数学创新,毕竟是一项困难的挑战。与之相比,在通用人工智能系统中实现对于日常对话与数字表征的整合,看上去要容易一些。按照“先易后难”的原则,我们必须将对于后者的实现视为日程表上的首选任务。有鉴于此,在下面的讨论中,笔者会将注意力更多地集中于这项比较容易完成的任务上。
在展开正面的阐述之前,笔者还需要对“目前主流人工智能系统是否能够应对上述两项挑战”这一问题给出评估意见。而笔者的相关评估意见乃是消极的。在笔者看来,为满足特定需要而产生的主流人工智能系统,既不能有效地评估特定数学表达式的实践价值(这属于前文所说的“较为容易的任务”),遑论进行数学创新(这属于前文所说的“较为困难的任务”)。
不过,或许有人会举出例证,反对笔者的上述评断。例如,有人可能会认为“自动数学家系统”(Automated Mathematician,缩写AM)2 构成了笔者论断的一个反例,因为据称该系统可以自动地发现哥德巴赫猜想的内容和一些基本的算数定理。然而,正如勒纳特(Douglass Lenat)与布朗(John Brown)3 所指出的,这个系统之所以能够发现那些数学对象,乃是因为系统中存在着特定的LISP语言短程序;而只要没有系统外的人类研究员用复杂的数学概念来解释这些程序的运行,那么,该系统的上述数学发现就会泡汤。因此,从认识论角度看,AM自身并不真正理解它的“发现”,因为只有当某主体能够运用其自身的内部认知架构来解释某事时,该主体才算得上真正“理解”了这件事。从这个角度看,AM肯定是缺乏数感的,因为数感的存在本身就预设了一种解释数字表达式的能力。无独有偶,在业界颇有名气的“培根系统”(BACON)4 也有同样的毛病。该系统据称能重新发现一些重要的物理学定律(如理想气体定律、开普勒第三定律、库仑定律、欧姆定律、伽利略单摆定律和恒定加速度定律等)。从认识论角度看,培根系统其实也无法真正理解其发现,因为在该系统中出现的数学变量的物理意义恰恰是由人类设计师预先赋予的——至于该系统自身,则不能对这类变量给出任何一种元描述。也因为这一点,培根系统不可能获得数感,因为数感的存在本身就预设了对于数学变量的意义加以解释的能力。
然而,上述对于主流人工智能系统的批评性断言是否犯下了“以偏概全”的谬误呢?在自动数学家系统与培根系统之外,是否还可能存在着别的能够拥有数感的主流人工智能系统呢?而笔者接下来要论证的就是:只要一个人工智能系统不是通用人工智能系统,它在原则上就是“不识数”的。
三、为何主流人工智能系统均是天生“不识数”的
一般而言,主流的商用计算机均是“数码化”的,因为它们的内部语言通常是基于八进制或十六进制的编码来运行的(顺便说一句,八进制或十六进制乃是二进制的某种变种)。对于LISP这样的高级编程语言来说,它们的运行也是基于上述编码的。但是主流计算机的这种“数码化”,是不足以使其产生“数感”的。为何这么说呢?这是因为,一个主体若要有健全的数感,就需要知道在特定语境中一个数字到底算不算“大”,而要做出这种判断,该主体就需要在不同语境中选择不同的“参照物”来决定对象到底算不算“大”。这里的参照物其实并非一个静态的对象,而是对于多项要素综合评估后产生的结果。而这些要素包含了系统的任务截止时间点、剩余时间、剩余电量、知识库内容、硬件条件等异常丰富的内容。我们将这些要素统称为“运行资源”。譬如,对于一个运行资源相对丰富的系统来说,10分钟的任务解决时间限制就会显得很“宽松”,而对于一个运行资源逼仄的系统来说,同样的时间量则会显得“不够用”。很显然,要对系统的运作资源进行整体概观,系统自身就要对其内部运行条件与其周围环境之间的动态关系进行把握。由于这种动态关系是依据语境变化而变化的,所以,相关的把握结果就不能在任何公理化的系统中被预先编码,因为任何一种公理化的知识库整合方式都是缺乏足够的语境灵活性的。
以上述结论为出发点,我们也可以重新理解上一部分对于自动数学家系统与培根系统的评论。这两个系统都是公理化的,因为在这两个系统中,程序员必须预先固定好一些特定数量的结构性要素。而既然这些要素已经被固化,此类设计思路便会使得相关的系统无法灵活应对各种应用语境的变化。例如,自动数学家系统就包括了上百个被称为“概念”的数据结构、上百个“启发式规则”以及一个简单的控制流。然而,若没有人类的干预和解释,该系统是无法自主调整这些要素的。与之类似,就培根系统而言,虽然貌似能够处理大量与特定物理学法则相关的数据,但是关于“哪些数据值得成为备选的物理法则的奠基性证据”这个问题,却是无法进行自主思考的。毋宁说,程序员会预先告诉系统哪些数据是具有“物理学价值”的。但这就等于将科学发现的最重要步骤“分包”给人类完成了。从这个角度看,培根系统只不过就是人类智能的副产品罷了。
那么,公理化进路的人工智能系统就没有别的办法来应对语境灵活性了吗?譬如,设计者能够在系统中设定某些“元公理”,以便预先规定好某些特定的知识模块和某些特定种类的语境之间的联系,这样的系统难道就不能让自己的行为具有语境灵活性了吗?很可惜,对于上述问题的回答乃是否定的,因为再多的“元公理”也不可能穷尽所有的知识模块与语境之间的联系。以古哈(Guha)1的“微理论”为例(微理论乃是为“Cyc系统”而设计的一个辅助性的概念工具):他以微理论为基础,对Cyc系统的知识库加以重新组织和分类,使之成为一些更易处理的知识模块,而每一个微理论则包括几条可以被进一步测试或打磨的公理或规则。那么,此类设计是如何使恰当的知识模块能够在恰当的语境中得到恰当的调用呢?其诀窍便是在诸微理论之上再去设定作为其元公理的“表述规则”,以便预先规定在哪些语境中一个微理论有权调用另一个微理论所导出的结果。不过,即便整个设计方案已然假定了设计者能够预知在每一个工作情境该用何种微理论,但是谁又能有这种神一般的预知力呢?
有人或许会问:上述的诊断意见都是针对“符号主义进路的人工智能系统”的,那么,该诊断是否也适用于联结主义或深度学习进路的人工智能系统呢(顺便说一句,由于深度学习技术只是传统联结主义技术的升级版,下面我们将仅仅提及联结主义进路的人工智能系统)?
笔者认为,对于上述问题的回答乃是肯定的,尽管从表面上看,对于联结主义进路的人工智能系统的构建思路,的确不同于符号主义的人工智能系统。概而言之,构造一个联结主义网络的基本思路便是去构造一个高度简化的神经网络模型。这样的模型通常包括一个输入层、几个隐藏层以及一个输出层,而其中每一层都包含大量的人工神经元节点。在“有监督学习”模式的人工联结主义模型中(这是一种最典型的联结主义构造模式),对于系统的训练是离不开大量学习样本的“喂入”的。 而一个相关的训练样本在被系统处理之后,系统会立即判定实际的处理输出与目标输出之间的差值——如果此差值过大,以至于实际输出必须被视为“误差”,那么,该系统会依据特定的学习规则来调整节点间的联结权重。经过一系列的此番调整,神经网络所产生的输出就会越来越接近目标输出,直至训练达标。
然而,上述技术路径依然不足以让相关的系统产生那種足以灵活地适应多样性语境的“数感”。其原因是:一个系统要有健全的数感,就必须把握评价性词汇(如“大的”“足够的”等)、数字表达式与语境要素三者间的关系,故而,训练一个联结主义网络所用的训练样本,也必须包含所有这三类要素。但这一点是不可能实现的,因为我们根本不可能在训练样本中包含语境要素。这又是为何呢?这是因为:语境要素本身就是一个囊括很多下级要素的高阶概念,而联结主义网络的输入单元层一般只对训练样本的低阶特征敏感。因此,从原则上说,除非我们让语境概念的含义缩水,否则,就无法通过训练一个联结主义网络来让其获得真正的语境灵活性(顺便说一句,某些深度学习系统貌似能够处理一些“语境”,但这种“语境”仅仅指文本的前后文关联,而无法囊括更多的要素,因此,非上文所讨论的“语境”)。
对于主流人工智能系统的批评,就到此为止了。下面,我们将转入对机器“数感”的实现方案的尝试性讨论。
四、如何在纳思中表征数量
在下文中,笔者将依据非公理化推理系统(Non-Axiomatic Reasoning System,缩写NARS,汉译为“纳思”)所提供的技术刻画手段1来讨论“如何实现机器数感”这个问题。纳思是一个通用推理系统,而非针对特定知识领域的专用推理系统。除了通用性之外,它与传统推理系统的不同处还在于:即使没有得到用以完美解决问题所需要的充分知识与充足时间,该系统也有能力从自身的有限经验出发进行学习,并对给定的问题提供某种尚可被接受的解法。研究纳思的目标有两方面:首先,此类研究有助于理解一切智能系统的规范性特点;其次,此类模型能够提供一个计算模型来描述“会思考”的机器,以直接助力通用人工智能系统的研究。目前,纳思研究计划也被视为方兴未艾的 “通用人工智能运动”的一个代表性技术流派。2
那么,我们究竟该如何在一个纳思中实现机器数感呢?在这方面,发展心理学关于孩童如何学习数学过程的研究成果,或许颇有参考价值。3 也就是说,我们要将纳思也视为某种意义上的孩童,就像教育孩童那样去教育这样的人工智能系统。比如,我们首先要教会纳思那些最具体、最基本的数学概念,然后一步步地将我们的教学目标过渡到那些更抽象的概念。那么,什么才是最具体、最基本的数学概念呢?或许不是自然数,而是那些自然语言中的量词(如“有一些”等)。譬如,对于孩童而言,在把握“一”或“二”这些概念之前,或许得先学会说“有一些糖果是红的,而有一些则不是”,这就预设了他们已学会诸如“一些”“大多数”之类的量词。
对于数学哲学中的逻辑主义流派4 较为熟悉的人可能会说,笔者提出的思路无非就是弗雷格或罗素式的逻辑主义思路的翻版,即以量词为基础,将数学还原为逻辑。但上述印象乃是错误的。在弗雷格或罗素式的一阶谓词逻辑中,所谓的“量词”便只有“存在量词”和“全称量词”两种而已,难以有效地涵盖自然语言中那些表述不同程度的量词,如“很少”“一点点”“一些”“大多数”“几乎全部”等。与之相较,笔者提出的纳思式进路,正是要顾及在日常语言中的这些常见量词。
那么,我们该如何对这些量词进行技术刻画呢?
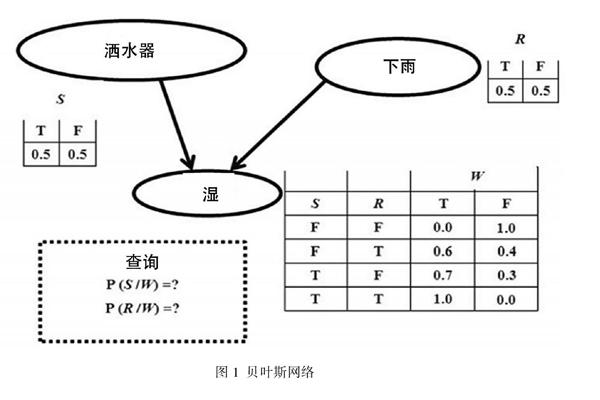
在纳思中,概念节点A与B之间的连接强度,可以被理解为主项的成员从属于谓项的成员的程度,而这样的强度或者程度可以被进一步地表现为A与B之间连线的“宽度”或者“权重”。这一点或许会让人联想起贝叶斯网络(见图1),因为连接贝叶斯中诸节点的那些通路的权重,也能对一个事件引发另一个事件的概率值进行编码。
然而,纳思网络与贝叶斯网络尚有两点重要差异。
差别之一:在纳思最为基础的表征层次上,诸纳思节点所编码的,基本上是像“苹果”或“红”这样的概念,而不是代表事件的命题(如图1所展现的那些事件: “天在下雨”“洒水器开着”“草坪湿了”等)。因此,在图2中,两个纳思节点之间虽然有一个箭头将其联系到了一起,但这并不代表一个事件相对于另一个已被给定的事件的后验概率,而仅仅代表某个主谓判断——如“渡鸦是黑色的”——的强度(不过,更为复杂的纳思构造物,还是可以通过某些纳思节点来编码复合词项和命题的,但不在本文的讨论范围之内)。
差别之二:在贝叶斯网络中,数据的更新规则必须能用标准的概率论规则来解释,而纳思的数据更新规则和标准的概率论规则却有很大不同。依据标准的概率论,证据池中的证据被获取的时间先后关系,与基于此池中证据的相关假设的成真概率并没有本质性联系,因此,一个严格基于标准概率论运作的智能系统是不可能产生“锚定效应”的(即一种特定的心理学效应,以使那些先被获取的证据,比那些后获取的证据,更能影响主体对于相关假设成真概率的判断)。然而,纳思却可以模拟“锚定效应”的产生,1 以便应对某些需要系统急速做出判断的问题处理情景。
下面我们就通过具体的例子,来说明纳思是如何处理数量关系的。
假定该系统观察到了10只渡鸦,其中有9只是黑的,由此形成了一个基本的纳思式判断“渡鸦→黑色的”(意思即“渡鸦是黑的”)。有两个参数可以用以刻画这样一个判断的真值,一个是频率因子(f值),另一个是置信因子(c值)。对于f值而言,其计算公式是:
公式1: f = w + /w
在此,“w”代表系统所获取的用以支持或者反对某假设的证据总数(在上述案例中,该值乃是10,因为系统的确观察到了10只渡鸦),而“w + ”代表其中正面证据的总数(在上述案例中,该值乃是9,因为的确有9只黑渡鸦被观察到了,以便从正面支持“渡鸦是黑色的”这个假设)。但需注意的是,这里的f值并不能通过对于概率的 “频率主义解释”1 来解读,因为根据“频率主义”的假定,一个系统是应当有无穷的时间来收集证据的,而纳思则完全没有采用这个假定。毋宁说,即使纳思搜集证据的时间非常有限——这往往体现为一个很小的w值——该系统也能给出一个f值。
然而,仅仅依赖f值,纳思对于判断的真值的刻画还是很不完整的。这种不完整性,可以通过对下述问题的考虑而得到揭示:现在假定系统已经观察到了100只渡鸦,其中有90只是黑色。根据公式1,现在f值还是0.9。然而,我们的直觉似乎是:该数据要比旧的数据更为可靠,因为它基于一个更大的证据池。如何在纳思中刻画这一区别呢?光有f值恐怕不行,我们还得引入c值:
公式2: c=w/(w + k)
依據公式2,基于100份关于渡鸦的证据的f值(例如0.9),会被赋予一个更高的c值,而基于10份关于渡鸦的证据的f值虽然也可能是0.9,但却会被赋予更低的c值。由此,就形成了两个不同的数对,用以刻画两个不同的纳思判断的真值。很明显,即使f值相同,两个具有不同c值的纳思判断,其各自所导致的推论的强度也会不同:c值越高,从中导出的结论的强度也越高,反之亦然。
对于公式2的观察还能告诉我们:当k取某常数时,w值越大,c值越接近1。不难想见,当w值已经变得很大时,它若变得更大,这一点并不会导致c值被明显地提高。这样一来,对于纳思而言,系统所先得到的证据,在权重方面也会高于其后所得到的证据。这便等于是在纳思中模拟了“锚定效应”。这就使得系统不会陷入不断搜集新证据的怪圈,而在基本证据量大致足够的情况下就产生出足够高的c值。
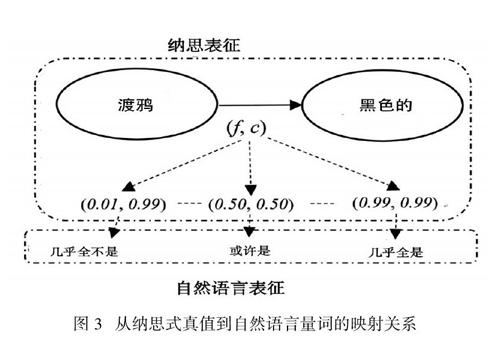
不同的f值和c值所构成的数对,可以被映射到诸如“很少”“一点点”“一些”“大多数”“几乎全部”等自然语言中的量词上(见图3)。但需要注意的是,当这些量词在自然语言中被表征出来的时候,其背后的f值、c值、w值与 w +值均不会直接出现,而只会在系统的后台运作中出现。这就好比说:当一个儿童觉得他所见过的大部分渡鸦都是黑的时,他或许已经遗忘了其所观察过的渡鸦的精确数量。
有了上面的讨论做基础,我们似乎就可以讨论如何在纳思中表征自然数了。但在切入此话题前,我们还有一项预备工作要做。
五、如何让纳思学会“the”(“这个”或“那个”)
很多人或许会想当然地认为,如果我们要让通用人工智能系统学会自然数,那么相关的教学起点就应当是所有的自然数中最小的“一”。然而,这可能不是一个好主意,因为“一”可能还是一个过于抽象的概念。笔者的建议是:从定冠词“the”开始教。
为何要这么做呢?因为用“the”这个英语中的常见定冠词时,说话人一般都会借此表示其背后所跟的对象在谈话语境中的唯一性。比如,说“the old man”(那个老人)时,说话人一般就会预设在谈话语境中仅有一个老人。上述分析其实也适用于汉语。虽然在汉语中没有与“the”严格对应的单个的词,但类似的现象也是有的。“the”一般在汉语中被翻译为“这个”或“那个”,而当我们说“那个老人”的时候,我们往往也预设了语境中被涉及的老人只有一个。当然,笔者也注意到,西方语言哲学界近来有一种研究趋势,即否认“the”之后所跟的对象在语境中是唯一的,1 但为了讨论的简洁计,笔者在此尚且不想处理这一新的学术见解。
那么,为何要让纳思先学会说诸如“The raven is black”(这个渡鸦是黑色的)这样的句子,而不是先让其学会“一”呢?这样做的理由,乃是基于如下的三步论证:
第一步:一个智能系统要具有计数能力,首先就得具备辨别物理对象数量的能力。
第二步:仅仅让系统知道“一”的意义,并不能使相关的智能系统具有上述的识别能力,因为抽象的“一”自身并不和物理对象相关联。
第三步:与之相较,让系统首先领会“the”的意义,则可能让系统更快地掌握识别物理对象数量的能力,因为根据“the”的基本用法,它是必须引导其后面所跟的那些要被计数的物理对象的名称的。
那么,我们究竟该如何在纳思中刻画“the”呢?一些人可能不禁想引用罗素对“the”的处理方案。2 依据该方案,“The raven is black”这句话必须被重述为:
?x[(Rx & ?y(Ry → y=x)) & Bx]
其自然语言翻译是:存在至少一个对象,该对象是渡鸦;如果存在另一个事物也是渡鸦,那么这第二个事物无非就是第一个,而且它是黑色的。
然而,笔者不会采用罗素的上述处理方案。很明显,他的处理方案预设了存在量词和全称量词的基础地位。但正如前文所述,这种预设使我们无法自然地处理自然语言中表示数量多寡不同程度的诸种量词。所以,纳思对于“the”的处理基本上会另辟蹊径。
不过,罗素对“the”的处理也有一个值得赞许的地方,就是他区分了“摹状词”(如“the present French king”,即“当今法王”)和“逻辑专名”(如“this”,即“这个”)。依据罗素的观点,虽然由“the”开头的摹状词与逻辑专名都表明了它们所指的事物的唯一性,然而,二者依然有所分别。具体而言,逻辑专名与其外在对象之间的联系更为直接,因为逻辑专名除了有指涉功能外,其本身不具有任何意义,而摹状词依然具有意义。
从纳思的角度看,罗素的上述说法至少包含了一半的真理,尽管它也包含了一半的谬误。此说的错误之处在于:即使如“这个”(this)这样的逻辑专名,其实也不是完全没有意义的,因为至少它表达了说话者和对象之间的距离。而此说所包含的真理性则在于:逻辑专名“这个”(this)的意义毕竟是非常稀薄的,以至于它大致能被视作为别的意义提供支点的一个“光裸”的载体。也正因為逻辑专名“这个”(this)的意义是贫乏的,它就特别适合成为教授自然数时所用的“教具”,因为在计数活动中人们的意向活动真正瞄向的并不是物理对象的数量,而是物理性质附着于其上的那些载体的数量。
那么,我们又该如何在纳思中表征逻辑专名呢?从句法上说,逻辑专名跟其他纳思词项(或者节点)之间的区别主要在于:逻辑专名的外延里只有一个实例,而后者则有一个以上的实例。什么叫“外延”呢?在纳思中,一个词项的外延,就是作为该词项的主词出现的那些节点。那么,什么叫“主词”呢?在纳思中,对两个变元x和y而言,x是y的主词,当且仅当“x→y”的句法结构出现。有了上面的定义后,逻辑专名本身就可以通过对纳思网络的局部拓扑学结构的识别而得到计算机的自动定位。
另外,从语义学角度看,纳思中所有包含逻辑专名作为其主词的基本断言,其实都表示了一个单称命题。这些命题的f值和c值都必须被设定得较高,以便彰显下述唯名论立场:无论从本体论立场看,还是从认识论角度看,那些关于个别事物的断言都要比关于个别事物之集合或类型的断言来得更为可靠。
基于上述分析,从纳思的观点看,当一个人说“那只渡鸦是黑色的”时,他其实是对如下两个命题有所断言:(1)这是一只渡鸦(该断言与一对较高的f值和c值相结合)。(2)这是黑色(该断言也与一对较高的f值和c值结合)。若用“a“”代表“这个”,则表征(1)和(2)的纳思网络的拓扑学结构便如图4所示:
人们或许会认为,教会纳思“识数”的下一个步骤就该是教会其掌握“一”的概念了。但是笔者接下来就要论证:在教会纳思“一”之前,我们首先要教会它“二”。
六、如何教会纳思“二”与“一”
为什么在教纳思学会“一”之前,要先教会其掌握“二”呢?这是因为,如果一个集合只有一个下属成员的话,那么该集合在成员数量方面的特征会变得过于稀松平常,以至于难以成为吸引注意力的显豁特征。举个例子:如果一名教师向学生展示一个橙子、一个苹果和一把刀的话,学生如何能很快地意识到这三个集合的共性就是它们都只有一个下属成员呢?要让学生尽快注意到一个集合只有一个成员,唯一的办法就是将该集合与拥有更多成员的集合相互比较。比如,将其与一个拥有两个成员的集合相互比较。但这一点就预设了纳思必须先掌握“二”这个概念。
在纳思里引入“二”的步骤如下:
第一步:我们要教会纳思两个句子,即“这只渡鸦是黑色的”和“那只渡鸦是黑色的”。这两个句子中的“这只”与“那只”实际上指称了两个不同的对象,因此我们就必须给它们指派两个不同的逻辑专名,如“a”和“b”(见图5)。
第二步:为了教学目的,假设a和b的指称都很相似,那么,两者之间有着很明显的类比关系(见图6)。
图6 纳思网络中两个同类型的单称判断在主项方面的相互类比关系
第三步:基于上述步骤,纳思会忽略a和b在其他方面的区别,由此将b视为a的另一个例。对于算术的教学而言,这一步是很重要的,因为一个系统要从事计数活动,就必须先忽略被计数的对象之间在物理性质方面的种种区别(见图7)。
图7 对于两个逻辑专名的等同化处理
第四步:现在纳思就得到了一个类似矩阵的网络:它包含两个a,从而每个a就像一个占位符,可以被任意其他符号替换,例如可以被替换成两个点。由此,此类节点的语义内容就被降到了最低,而其在相关推理结构中的拓扑学地位则得到了凸显。由此,我们就不妨引入一个新词来指称这个拓扑学结构。这个新词就是“二”,也就是我们在纳思里引入的第一个数词。一个知道了“二”的用法的纳思,实际上也就知道了:只要在系统的推理路径中观察到类似于图8中上半部分的拓扑学结构,就可以用“二”来替换这个结构;或反过来说,对于出现“二”的判断句,系统也可以进行反向处理,以复原出一个更为复杂的推理路径图。
图8 在纳思中引入“二”
现在总算到了教会纳思掌握“一”的时候了。但是如何从针对“二”的教学过渡到针对“一”的教学?
我们不能通过引入“减法”来从“二”得到“一”,因为“二减一等于一”这个陈述预设了“一”的概念。与之相较,从“二除以二等于一”出发来定义“一”貌似更为可行,因为“二”毕竟是纳思已经学会的一个概念。但是这个做法也预设了纳思已经理解了“除以”的意义。不过,这一预设还是会带来一些麻烦,因为抽象意义上的“除以”是很难被立即学会的。更可行的办法是用“取半法”(也就是分母为“2”的特殊除法)的概念来替代抽象意义上的除法。对于“取半法”这一概念的引入,可以通过下述操作来实现:对于任意集合,求它的两个等式的子集的分布方式。更具体而言,当我们让纳思求概念X之实例的半数时,纳思就会尝试着对原集合的成员进行随机二分,由此得到两个子集,然后一一比较这些子集的大小,直到找到两个等式的子集为止。计算机很容易通过对网络的局部拓扑学结构的检索来完成上述任务,所以,我们没有理由认为纳思无法执行这个“取半任务”。故而,只要纳思能对“二”的概念进行“取半”操作,它立刻就能得到“一”的概念。
现在,纳思已经学会了“二”与“一”这两个概念,由此也就有希望学会所有奇数和偶数。限于篇幅,在此不能详述纳思如何习得更复杂的算术概念。
需要注意的是,由于现代数学的高度复杂性,笔者认为不需要都依赖如此曲折的方式来教会纳思数学概念。如果我们仅仅要设计一个具有低级数学智能的系统的话,那么,我们可以仅仅在纳思中置入一些负责特定类型计算(如针对“对数”或“三角函数”计算)的专用计算模块。对于纳思的其他部分而言,这些模块的内部运行就是一些“黑箱事件”。也就是说,这个系统的其余部分仅仅需要知道:自己应该在什么时候启动这些模块,以及如何理解它们的输出。这就很像一个算术能力有限的人适应社会的方式——只要他知道怎么用便携式计算器,并读懂上面的数字,他就能适应。
从上面的分析来看,即便一个数学智能很低的纳思,也可以在日常对话中很灵活地处理数字表达式。下面就是对于这一点的更为详细的说明。
七、深入讨论(代总结):纳思如何在日常对话中做到“识数”
在本文第三部分,我们已经看到:传统符号人工智能系统无法依据语境的变化而将正确的评价标签(如“大的”“足够多的”“太多的”等)与正确的数字表征相对应。而这些系统之所以做不到这一点,乃是因为这些系统是公理化的。因此,除非程序员提前用某些元公理来锁定评价标签、数字和语境三者的关系,否则,这些系統是无法在不同语境中将同一个评价标签灵活地指派给不同的数字表征的。然而,人类的生活瞬息万变,除非该系统的设计者对人类生活的各个方面能够做到无所不知,否则,就根本不可能在系统中预装针对所有可能语境的知识调用元公理。此外,即便是联结主义或深度学习的系统,也无法解决这个问题。这是因为,要使这些系统学会将特定的评价词与特定的数量表征相互联系,就得预先喂给系统一些特定的“评价词—数量”匹配样本,作为训练的起点。但是,这些匹配样本又从何而来呢?在日常生活中,相同的数量词会在不同的语境中获得不同的评价词(在两个彼此不同的特定语境下,100000元和2元都有可能是“足够”的),这一点就会使深度学习所需要的样本特征变得非常不稳定,最终使此类机器学习根本无法进行。
而与上述传统路径相比较,纳思则可以轻易解决这一难题,因为在一个统一的纳思推理网络中,数字表达式本来就已经与表示物理对象的词项相互结合在一起了。因此,纳思始终知道:“纯粹的”数字只不过是从实际事态中抽象出来的量化刻画,而这些刻画随时可以被复原为与实际物理对象相互关联的原始状态。此外,既然在纳思中代表各类物理对象的节点的推理功能可以随着系统的学习过程做调整,那么,包括数字节点和非数字节点在内的复合节点的推理功能自然也可以随之调整。如果我们以建立诸如“足够”和“不足”之类的评价词与特定数量词之间的推理关系为目标的话,以下便是旨在做出这类调整的一个极简方案:
1.表征出系统所要达成的目标;
2.估算达成该目标所需的资源数量,并将其缩写为RR;
3.估算目前可用的资源数量,并将其缩写为RA(这里需要注意的是,有待评价的数字表达式,通常会采用RA的形式);
4.估算RA和RR的差值,如果由此算出“系统的剩余资源在达成当前目标之后,亦足以用来执行其他任务”,则将“足够”这一标签指派给RA,否则,将“不足”这一标签指派给RA。
显然,要将上述步骤一步步走完,系统就不得不与大量的语境因素打交道,如给定任务的内容、RA的值、RR的值等。因此,只要纳思的运作能随着这些语境因素的变化而变化,那么,纳思就能够以一种富有语境敏感性的方式做到“识数”。
当然,要在工程学的层面上实现上述目标,我们还需要付出很多具体的努力。但本文的概要性论述,已经为在通用人工智能系统中如何实现“人工数感”,勾勒出了一幅大致的路线图。
How Can an Artificial General Intelligence System
Acquire “Number Sense”?
XU Yingjin
Abstract: Number sense literally means some form of awareness of what numbers mean to the users of these numbers in their practical lives. Mainstream AI systems(symbolic AI and connectionism included), being digitalized notwithstanding, do lack number sense in the sense that they all lack the capacities of building pragmatic inferential pathways connecting numerical expressions with non-numerical ones in a context-sensitive manner. The tentative realization of a machine-based number sense will appeal to the Non-Axiomatic Reasoning System(or “NARS”, the adjective form of which is “Narsian”), and it is different from mainstream. AI systems in the sense that it has capacities for learning from its experience, and for delivering its solutions to the given problems even when it is working with insufficient knowledge and limited time budget. The guiding principle for training NARS to acquire number sense is to teach it the least abstract mathematical notions first, then move to more abstract ones step by step, just like how we teach children mathematics. The Narsian representation of the “logical proper names” plays a pivotal role in this machine-oriented pedagogy.
Key words: number sense; intuition; Artificial General Intelligence(AGI); Non-Axiomatic Reasoning System(NARS); logical proper names
(责任编辑:苏建军)
