动态规划在水库优化调度中的应用

公丽

摘 要 随着科学技术的发展，用于解决水库优化调度的数学方法越来越多，如线性规划法、非线性规划法、逐次逼近算法（POA）网络分析法、动态规划法、神经网络模型法、大系统分解法、遗传算法（GA）、免疫粒子群算法（PSO）等，其中应用较多的是线性规划法和动态规划法。动态规划法能适应径流、时间等因素的影响，是解决多阶段决策过程的方法，概念和理论比较简单，方法灵活，常为人们所使用。本文结合实例详细介绍了动态规划模型的建立，以及在水库调度中具体的应用。该方法的应用为水库调度提供了有力的根据，具有重要的价值意义。

关键词 动态规划 优化调度 数学模型

中图分类号：TV697 文献标识码：A 文章编号：1007-0745（2021）07-0060-05

1 优化的概述

在水库调度过程中，如何能兼顾防洪、灌溉、发电等综合效益，是当前面临全球水资源短缺且在一定量的水资源下的重要问题[1]。为了充分发挥水利水电工程的经济效益，需要进行水库优化调度。

1.1 水库优化调度的概念

水库优化调度是一个多阶段决策过程的最优化问题。水库优化调度是运用系统分析的观点和方法来研究水利水电工程的调度，即将一个水库或者水库群视为一个系统，水库来水量作为输入，防洪、发电等综合效益视为输出，库容的大小、水位变幅、机组装机容量等限制就是环境约束，通过建立以水库调度效益为中心的目标函数，拟定相应的约束条件，然后用优化的方法求解目标函数和约束条件组成的系统方程组，使得目标函数取的极值，即获得水利水电工程的最佳效益。

1.2 优化方法的概述

动态规划是最优化技术中一种适用范围很广的基本数学方法，是解决多阶段决策过程中最优化问题的一种数学方法[2]。应用水库是，将径流过程视为是确定的，把水库蓄水量进行离散作为状态变量，把放水量作为决策变量，把发电、防洪和灌溉综合效益作为目标，每一时段的放水量使整个周期内的目标函数值达到最大的决策组成的策略就是最优的调度方案。

2 数学模型及动态规划模型

数学模型是指为了某种目的，用字母、数字及其他数学符号建立起来的等式或者不等式以及图表、图像、框图等描述客观事物的特征以及内在联系的数学结构表达式。为进行水利水电工程优化调度而建立的数学模型，通常是由最优化的目标函数和约束条件两部分组成。

由贝尔曼提出的动态规划方法是按时间或空间将过程分解为若干阶段，是解决多阶段决策过程的一种优化技术。一般将蓄水量作为状态变量，放水量作为决策变量，用水量平衡方程作为状态转移方程，并按时间顺序划分为阶段，根据所求目标及贝尔曼最优原理写出递推方程。这样将具有最大量的变量的复杂问题分解为一系列简单的小问题用地推方法求解。下面介绍在数学模型和动态规划方法中的部分概念。

2.1 最优准则与目标函数

最优准则是衡量水库运行方式是否达到最优的标准。对于单目标或以某一目标为主的水库，最优准则较为简单，如：（1）以发电为主的水库，可以在满足其他部门用水要求的前提下，电力系统的电力支出是最小、系统耗水量最小或者系统发电量最多等。（2）对于以防洪为主的水库，可以是在满足其他综合利用的要求下，削减洪峰后的下泄成灾流量最小或超过安全泄量的加权历时最短的等。（3）对于多目标水库或者复杂的水利系统，则应以综合性指标最优为好，以国民经济效益最大或者国民经济费用最小等。

优化调度的目标函数的具体形式依据所拟定的最优准则而定，就拿以防洪为单一目标的水库来说，为了避免下游地区在洪水来临的时候造成太大的损失，一般都需要进行控制下泄流量，此时目标函数可以由三种形式：最大削峰准则、最短洪水淹没历时准则、最小洪灾损失或最小防洪费用准则。在本次论文的应用实例中，采用了最大削峰为目标函数，在入库洪水、区间洪水、防洪库容、下游允许泄量和溢洪道泄洪能力等均已知的情况下，最大削峰准则就是要在蓄满防洪库容的条件下尽量使下泄流量均匀。数学上已经给出了结论，当使下泄流量均匀的时，即使下泄流量的平方和最小。

2.2 约束条件

水库优化调度中的约束条件，一般包括水库运行中的蓄水位的限制、水库泄水能力的限制、水电站装机容量的限制、水库及下游防洪要求的限制和水量与电量平衡的限制以及调度时必须考虑的边界条件等，通常以数学方程的形式表达，包括等式约束与不等式约束，组合成约束条件组。

水库发电的约束条件一般有以下几个方面：

1.水库蓄水位的限制：各个时段的库容大于相应时段允许的最小库容和最大库容。

2.水电站机组容量的限制：各个时段水电站的出力大于水电站的最小出力和最大出力。

3.下泄流量约束：各个时段的下泄流量大于水电站的最小和最大下泄流量。

4.水量平衡方程：在某个时间段内，入库流量与出库流量之差等于库容的变化。

5.非负条件约束：qi>=0（i=1，2，3，4，.....T）。

2.3 階段变量、状态变量及决策变量

把调解期划分为T个时段，以i（i=1，2，3，......T）表示，其中i-1～i时段为当前面临的时段，将年内的离散时段取为阶段变量。以水库的蓄水位为状态变量，分别以Zi-1、Zi表示第i时段的初、末蓄水位，本阶段末的水库蓄水位即是下阶段初水库蓄水位。决策变量就是模型的目标变量，当以调解期内发电量最大为目标函数时，决策变量就是水电站发电出力，但本次论文是要求各时段的下泄流量，所以把水库各时段的放水量作为决策变量。

2.4 动态规划的递推方程

用动态规划方法解决水库的最优调度问题时，主要是逐阶段使用递推方程择优。递推方程的具体形式与递推顺序和阶段变量的编号有关，若逆序递推且阶段变量的序号与阶段初的序号一致时，水电站水库优化调度问题的递推方程式为：

式中：Ni（V（i-1），qi）为面临第i个时段在时段初状态为V（i-1）和该时段决策变量为qi时所得的出力;f（i+1）（Vi）为余留期最优出力之和;fi（V（i-1））为从第i个时段初库容V（i-1）出发，到第T个时段的最优出力之和。

本题就是用逆序递推法找最优的下泄流量。

3 应用实例

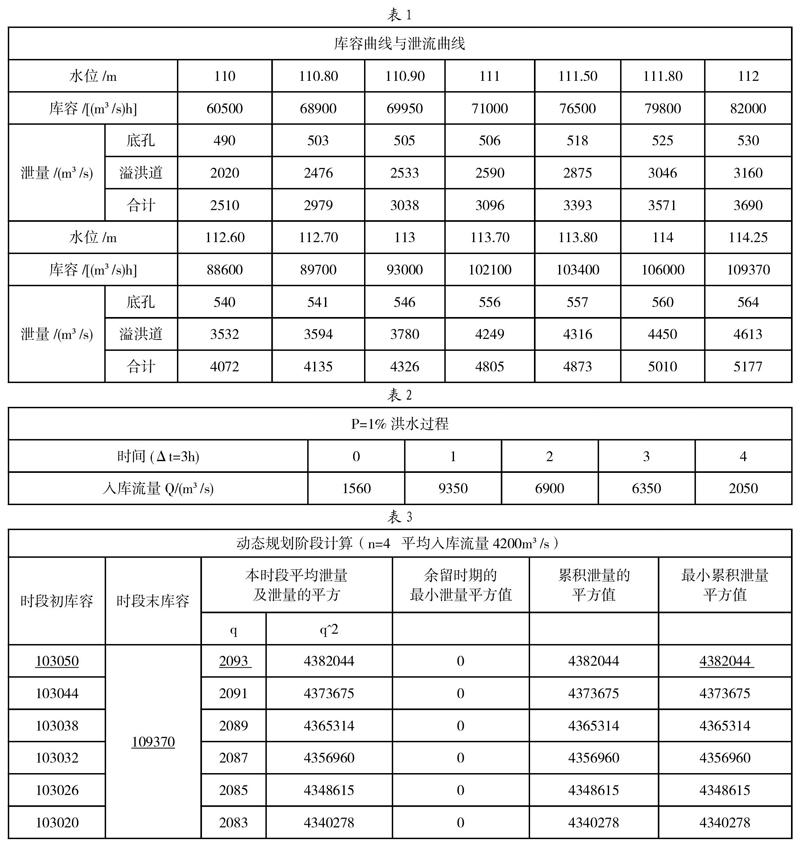
题目：某水库设有泄流底孔和河岸式溢洪道。防洪限制水位110m，设计洪水位115.9m，防洪高水位114.25m，水库库容曲线与泄流曲线见上表1。水库下游标准P=1%，当起调水位为防洪限制水位，遇P=1%洪水时，求以最大削峰准则的最优防洪调度过程（见上表2）。

解：将以上洪水过程划分为n=4个时段，将库水位110～114.25m防洪庫容按6（m3/s）h分格。然后逐时段运用动态规划的逆推方法求解。最大削峰流量的目标函数为下泄流量的平方和最小，可表示为：

式中：qi为第i时段的下泄流量;Qi为对应i时段的入库流量;Vi为第i时段的水库库容。

约束条件：

以上式子中：Qi为第i个时段的区间来水量;qi为第i个时段的下泄流量;V防为水库的防洪库容;Zi为第i时段初始时刻的蓄水位，Bi为第i个时段溢洪道的宽度;q（Zi，Bi）为第i个时段的最大下泄能力;q安为下游安全泄量;q汛限为汛期限制流量;Vi为第i个时段的水库库容。

建立逆时序的递推方程：

运用状态转移方程Vi=V（i-1）+（Qi-qi）Δt，可求得各对应时段末库容的泄量，其中Qi为时段平均入库流量。保留满足诸约束条件的q值，并平方，再与余留期的最小泄量平方值相加，求得相应于某一时段初库水位的下泄流量平方和最小值，即最优子策略。一直到n=1的第一时段，即可得最优防洪调度线。计算期末和计算期初库容是已知的定值（见表3～表6）。

由表6可知，最小累积量平方值min∑qi^2=16610557，对应的第一阶段初库容为60500（m?/s）h，时段末库容为71632（m?/s）h，第一阶段最优泄量为1744，对应的余留时期最小泄流平方值为13569021（m?/s）h，由该值对应到第2阶段可得，相应的时段末库容为90018，第二阶段最优泄量为1996，对应的余留时期最小泄量平方值为9585005，由该值对应到第三阶段可得，相应的时段末库容为103050，第三阶段最优泄量为2281，对应的余留时期最小泄量的平方值为4382044，由该值对应到第四阶段可得，相应的时段末库容为109370，第四阶段的最优泄量为2093，由此逆推得整个防洪优化调度过程。

故min∑qi^2=16610557（m?/s）^2，所得最优调度库容是由防洪限制水位对应的60500（m?/s）、71632（m?/s）、90018（m?/s）、103050（m?/s）至防洪高水位对应的109370（m?/s）。

综上，本例求得的最优调度线是由防洪限制水位110m经111.06m、112.73m、113.77m再到114.25m，各时段最优泄量分别为1744（m?/s）、1996（m?/s）、2281（m?/s）、2093（m?/s）。

4 结语

动态规划基本原理简单明了，容易理解，方法比较灵活，结果精度较高，被广泛的应用于各个领域。

参考文献：

[1] 杨峰，黄怀礼，张强.用动态规划法对水库进行优化调度[A].河南科学，2005，23（01）：17-19.

[2] 许新发，黄俊民.动态规划[J].江西水利科技，1995，21 （04）：234-238.