NOBEL:一种基于拓扑信息与监督学习的蛋白质复合物识别方法
2021-10-19王晓旭刘晓霞
王晓旭,刘晓霞
(大连海事大学 信息科学技术学院,辽宁 大连 116026)
0 引言
蛋白质作为生命的物质基础,在细胞的生命活动中发挥着关键作用。由于蛋白质并不是单独作用,而是与其他蛋白质一起形成复合物。因此,识别蛋白质复合物对全面了解细胞组成和生命过程具有重要意义。虽然蛋白质复合物的识别方法有很多,如串联亲和纯化(TAP)和质谱法可以直接识别蛋白质复合物,但这种实验方法要耗费大量的人力资源,因此如何快速、高效地从蛋白质相互作用网络中识别蛋白质复合物成为了关键性问题。
近年来,随着高通量技术的快速发展,产生了大量的蛋白质-蛋白质相互作用(PPI)数据[1]。这使得利用计算方法从蛋白质关系网络中识别蛋白质复合物成为可能。到目前为止,研究者提出了许多识别蛋白质复合物的计算方法。我们可以将这些方法分为无监督学习算法和监督学习算法。无监督学习算法是基于预先定义的规则来预测蛋白质复合物的方法。大多数的无监督学习方法都是利用PPI网络的拓扑信息识别蛋白质复合物,然而PPI网络中存在大量的假阴性和假阳性数据,使其不能获得令人满意的结果。监督学习算法是充分利用已知复合物进行训练并预测蛋白质复合物的方法。虽然现在的蛋白质复合物研究中存在大量的已知复合物,但仍有许多蛋白质复合物未被发现,如何从有限的已知复合物中获取充足的信息是监督学习算法的关键问题。
本文提出了基于已知蛋白质复合物拓扑信息和监督学习的蛋白质复合物识别算法(Protein Complex by Supervised Learning,NOBEL)。我们利用GO注释和拓扑信息对PPI网络加权,并从加权网络和未加权网络中提取已知蛋白质复合物丰富的拓扑信息作为特征。通过这些特征来训练模型,然后将训练后的模型应用于完全子图的过滤、扩张和候选复合物的合并,得到最终预测的蛋白质复合物。实验结果表明,与现有蛋白质复合物识别方法相比,我们的方法能有效提高蛋白质复合物识别的性能。
本文组织结构如下:第1节介绍国内外研究现状以及和本文研究相关的工作;第2节对本文提出的蛋白质复合物识别算法NOBEL进行详细说明;第3节是实验验证和实验结果分析;第4节是论文总结和下一步工作展望。
1 相关工作
蛋白质相互作用网络通常被描述为一个无向图,其中,节点表示蛋白质,边表示为蛋白质间的相互作用。而蛋白质复合物通常对应于PPI网络中的稠密子图,这使得研究人员可以运用PPI网络的拓扑特性识别蛋白质复合物。MCODE[2]是被提出最早的蛋白质复合物识别算法之一。其首先为节点加权,并选择权重最高的节点作为种子节点;然后,迭代的选择其邻居节点来扩张种子节点,形成候选复合物。ClusterONE[3]是一种新的衡量子图的内聚性的计算方法,它选择度较高的节点作为种子节点,然后使用贪婪算法扩展种子节点,使子图获得更高的内聚性,直到没有种子节点。SE-DMTG[4]通过公共邻居和GO注释为节点加权并排序,然后选择权重最高的节点为种子节点,并应用迭代贪婪搜索扩展种子节点生成蛋白质复合物。HGCA[5]根据聚类系数和节点度提出了一种新的节点度量方法来量化节点的重要性,然后选择权重最高的节点为种子节点,并通过聚类模型扩张种子节点,形成最终复合物。
CMC[6]是基于最大子图的蛋白质复合物识别算法。它首先为PPI网络加权,然后从加权网络中搜索最大子图,并计算子图加权密度,合并高重合的子图形成蛋白质复合物。COACH[7]是一种经典的核心节点—附着结构的蛋白质复合物识别算法。它首先识别小的密集子图,再通过合并这些密集子图生成核心节点,然后将附着蛋白连接到核心。Meng等人提出了DPC-HCNE[8]算法,它首先通过启发式的分层压缩将PPI网络压缩成更小的PPI网络。然后应用网络嵌入算法DeepWalk构建加权PPI网络,最后采用核连接聚类方法识别蛋白质复合物。Xu等人提出了CPredictor2.0[9]算法,它首先将功能相似的蛋白质分组,然后利用马尔可夫聚类算法对各组进行聚类分析,并合并重叠的蛋白质复合物。Wang等人提出了EWCA[10]算法,它利用节点与其邻域的结构相似性来确定核心。另外,它提出了一种新的识别附着蛋白的方法,将附着蛋白加入相应的核心形成蛋白质复合物。GANE[11]算法利用团挖掘方法生成候选核心,然后从候选核心中选出种子核心。如果蛋白质与种子核心的连接程度超过阈值,则把该蛋白质作为附着蛋白加入核心得到蛋白质复合物。
在现今的蛋白质复合物研究中,已经存在了大量的已知蛋白质复合物。监督学习方法可以利用已知蛋白质复合物的信息识别新的蛋白质复合物。Yu等人提出了SLPC[12]方法,该方法首先由加权和未加权网络得到蛋白质复合物的特征并训练逻辑回归模型;然后从PPI网络中发现最大子图作为核心,并使用模型为核心添加附属节点得到蛋白质复合物。Zhu[13]等人提出了一种半监督的网络嵌入模型,它首先选择关键邻域节点为顶点属性并得到顶点的一阶近似,然后它设计三层GCN计算顶点的二阶近似,最后优化一阶近似和二阶近似得到模型并利用模型识别蛋白质复合物。Liu[14]等人提出了一种基于网络嵌入的监督学习方法,它首先从PPI网络中获得节点嵌入并构建加权PPI网络,然后采用监督学习方法识别蛋白质复合物,最后利用随机森林模型筛选候选复合物。Xu等人提出了XGBP[15]方法,它首先提取蛋白质复合物的拓扑信息作为特征并训练XGBoost模型,然后从PPI网络中选取种子节点,并运用贪心算法扩展种子节点得到候选蛋白质复合物,最后应用XGBoost[16]模型对候选蛋白质复合物分类。Faridoon[17]等人将支持向量机与ECOC算法结合,以氨基酸的物理性质和各种拓扑信息作为特征,从PPI网络中识别蛋白质复合物。
2 算法详述
本节将详细介绍我们提出的蛋白质复合物识别算法NOBEL。NOBEL包含四个部分:①网络加权; ②复合物特征; ③训练模型; ④蛋白质复合物识别。
2.1 网络加权
本文结合蛋白质的生物信息和PPI网络的拓扑信息,来衡量蛋白质间的可信程度,进而构建带权重的PPI网络。为了计算蛋白质间的拓扑相似性,我们引入了Wang[10]等人提出的基于Jaccard相似系数的相似性度量HOCN。两个相邻蛋白质v和u的Jaccard相似系数定义如式(1)所示。
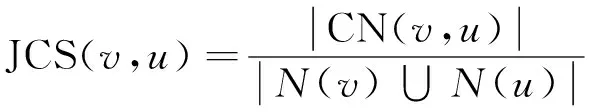
(1)
其中,N(v)和N(u)分别表示v和u的邻接点集合,N(v)∪N(u)表示v和u的邻接点的并集,CN(v,u)表示v和u的公共邻接点集合,即N(v)∩N(u)。|N(v)∩N(u)|表示v和u的公共邻接点的个数,|N(v)∪N(u)|表示v和u邻接点并集的个数。
HOCN的定义如式(2)所示。
HOCN(v,u)
(2)
蛋白质v和蛋白质u的拓扑相似性还与它们公共邻域与边(v,u)的连接程度有关。公共邻域与边(v,u)的连接程度定义为CNS,如式(3)、式(4)所示。
JCS*=JCS(v,w)*JCS(w,u)
(3)
(4)
基因本体GO包含描述基因和蛋白质的生物学术语。GO中最基本的概念是术语(Term),本文根据GO术语的数量和GO术语注释蛋白质的个数计算蛋白质间的生物相似性。蛋白质v和u的生物相似性sim(v,u),如式(5)所示。
(5)
其中,C(v,u)表示蛋白质v和u被相同的GO术语标注的GO术语集合。Si(v,u)(1≪i≪n)表示在蛋白质v和u共同拥有的GO术语中,每个GO术语标注的蛋白质的集合。Smax表示在所有的GO术语中,一个GO术语标注的蛋白质个数的最大值。
我们结合蛋白质间的拓扑相似性与生物相似性计算蛋白质v和u的相似性,其定义如式(6)、式(7)所示。
2.2 复合物特征
如何从蛋白质复合物中提取关键的特征是我们研究中的关键问题。到目前为止,研究者们在这方面已经做了很多相关研究。本文根据加权和未加权网络中提取蛋白质复合物的16个特征。特征的详细描述如下所示。
(1)密度:对于无权图,设G=(V,E)有|E|条边,则密度定义为|E|除以图中理论上最大可能的边数|E|max,|E|max=|V|×(|V|-1)/2。对于加权图,设G=(V,E,W),边(v,u)的权重为w(v,u),其密度定义如式(8)所示。
(8)
(2)度统计:对于无权图,节点度定义为节点的邻居节点数;对于加权图,节点度定义为节点与其相连节点间权重之和。本文选择加权图和未加权图中节点度的最大值、平均值和中位数作为子图特征。
(3)边权重统计:边权重是加权图的重要特征。本文中我们选择子图中所有边权重的平均值和方差作为子图的特征。
(4)度相关属性:度相关属性可以测试子图中节点与其邻居节点的连通性。对于每个节点,其定义为该节点最近邻居节点的平均连接数目,即平均度。我们选择子图中节点度相关属性的平均值和方差作为子图的特征。
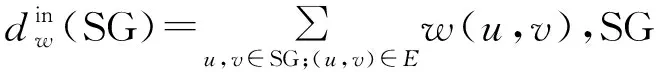
(9)
(6)聚类系数:对于无权图来说,节点v的聚类系数是通过它的三角形个数与可能形成的三角形个数比,其定义如式(10)所示。
(10)
其中,T(v)表示经过节点v的三角形个数。我们选择无权图中聚类系数的方差作为其聚类系数特征。加权图中聚类系数定义如式(11)所示。
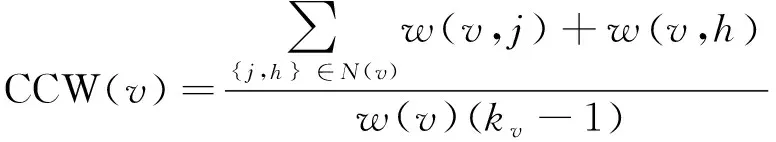
(11)
w(v)=∑j∈N(v)w(v,j)
(12)
其中,kv表示节点v的邻节点数目,w(v,j)表示节点v和j之间边的权重。w(v)表示节点v与所有相邻节点之间边的权重和。我们选择加权图聚类系数的平均值和最大值作为聚类系数特征。
2.3 训练模型
监督学习方法有回归和分类两种类型,而蛋白质复合物识别属于分类问题。我们应用监督学习方法判断一个蛋白质子图是否为真实蛋白质复合物。本文经过实验分析应用SVC[18]方法来评估子图是蛋白质复合物的可能性。SVC是支持向量机算法的一种,主要用于解决分类问题。相比其他分类方法,SVC需要的样本数据相对较少,并且由于SVC引入了核函数,对于高维或非线性的数据样本SVC也能轻松应对。
本文分别从正例和负例中提取相应的特征,并结合正负例特征得到数据集D。我们把数据集D分为训练集和测试集,其中,训练集占70%,测试集占30%。构造完训练集后,我们将训练集作为输入数据训练SVC模型。本文中使用的模型参数设置如表1所示。

表1 模型参数设置
2.4 蛋白质复合物识别
在本节中,我们应用上述训练的模型识别蛋白质复合物,该方法可以分为三部分:子图选择、子图扩展和复合物过滤。
(1)子图选择我们使用Clique[19]算法搜索PPI网络中的最大子图,并选择蛋白质个数大于等于3的子图作为初始子图。由于初始子图之间可能会产生重叠,故需要对初始子图进行过滤处理。我们使用训练后的模型判断每个子图是真复合物的概率,并按概率降序排列。对于任意子图Ci,计算其与概率低于它的子图Ck间的重叠蛋白质个数,若重叠蛋白质个数高于给定的阈值α,则过滤子图Ci。重复上述过程,形成最终的初始子图集合,通过实验验证,阈值α设置为2。
(2)子图扩展对于任意子图Ci,其邻接点集合为N(Ci),选择N(Ci)中的任意一个节点v加入子图Ci。然后,使用训练后的模型判断{Ci∪v}是真复合物的概率,选择概率提升最高的节点v加入到子图Ci中。重复上述过程,直到N(Ci)中没有节点加入Ci。至此,子图Ci扩张完毕,形成候选复合物。
(3)复合物过滤候选复合物之间可能也会发生重叠,故需要对候选复合物做过滤处理。我们使用训练后的模型判断候选复合物是真复合物的概率,并按概率降序排列。对于任意候选复合物Ci,计算它与概率低于它的候选复合物Ck间的重叠率overlap(Ci,Ck),其定义如式(13)所示。

(13)
如果重叠率大于设定的重叠阈值β,则合并两个候选复合物并判断合并后的候选复合物{Ci∪Ck}是真复合物的概率。如果概率提升则两个候选复合物合并,否则过滤掉候选复合物Ck。重复上述过程,得到最终预测的蛋白质复合物。通过实验验证,重叠阈值β设置为0.8。
3 实验与分析
3.1 数据集
本文分别在四个大规模酵母PPI数据集上进行了实验,这四个PPI数据集分别是Gavin[20]、DIP[21]、WI-PHI_core[22]和WI-PHI_extend[22]。这四个PPI数据集的基本信息如表2所示。我们使用的标准蛋白质复合物数据集是CYC2008[23],并且删除了其中蛋白质个数小于3的蛋白质复合物,最后CYC2008含有236种蛋白质复合物。

表2 四个PPI数据集的基本信息
我们的训练数据包含正例和负例两部分,其中,正例是由MIPS[24]、SGD[25]、TAP60[20]、Aloy[26]四种常见的蛋白质标准复合物数据集合并组成。由于从PPI网络中识别的蛋白质复合物不包含PPI网络中不存在的蛋白质分子。因此,在不同的PPI网络上实验时,要过滤掉正例中不属于该PPI网络的蛋白质分子。同时,我们还过滤掉了正例中与CYC2008重叠的蛋白质复合物。我们的负例是从PPI网络中随机选取节点生成的,其大小与正例保持一致。正例和负例中蛋白质复合物包含的蛋白质分子个数都是大于等于3的。在四个PPI数据集上使用的正例和负例的基本信息如表3所示。

表3 四个PPI数据集上正例和负例的基本信息
3.2 评价指标
本文使用了两组性能评价指标,分别是:①F值(F-Measure)、准确率(Precision)和召回率(Recall); ②阳性预测值(PPV)、精确率(ACC)和敏感值(Sn)。
3.2.1F值、准确率和召回率
假设B={b1,b2,…,bm}和P={p1,p2,…,pn}分别表示标准蛋白质复合物集合和预测蛋白质复合物集合,选择一个真实蛋白质复合物b∈B和一个预测的蛋白质复合物p∈P,我们可以计算它们的邻域亲和度得分NA,其计算定义如式(14)所示。
(14)
其中,Vb和Vp分别表示复合物b和p中蛋白质分子集合,|Vb∩Vp|表示两个蛋白质复合物中共有蛋白质的数量。
一般来说,如果NA(b,p)>0.25,则认为两个蛋白质复合物是匹配的。我们设Ncb表示至少匹配了一个预测蛋白质复合物的标准蛋白质复合物的数量,Ncp表示至少匹配了一个标准蛋白质复合物的预测蛋白质复合物的数量。则准确率和召回率的定义如式(15)所示。
(15)
F值被定义为准确率和召回率的调和平均值,其定义如式(16)所示。
(16)
3.2.2 阳性预测值、敏感值和精确率
敏感值(Sn)和阳性预测值(PPV)的定义如式(17)、式(18)所示。
(17)

(18)
其中,n是标准蛋白质复合物的数量,m是预测蛋白质复合物的数量,Tij表示第i个标准蛋白质复合物和第j个预测蛋白质复合物共有蛋白质的个数。Ni表示每个标准蛋白质复合物中蛋白质的数量。精准率(ACC)是敏感值(Sn)和阳性预测值(PPV)的几何平均值,其定义如式(19)所示。
(19)
3.3 结果分析
3.3.1 与其他模型的比较
本文选择训练SVC模型用于蛋白质复合物识别。为了验证SVC模型的有效性,本文也选择训练其他监督学习模型识别蛋白质复合物。我们选择训练XGBoost、朴素贝叶斯(Bayes)、逻辑回归(Logistic)这三种监督学习模型并将它们的实验结果与SVC模型进行比较。SVC模型与其他监督学习模型比较的结果如表4所示。由表4可以看到,SVC模型与其他监督模型相比在Gavin、WI-PHI_core和WI-PHI_extend这3个数据集上都取得了最优的性能,且在F-measure指标上均优于其他模型。在DIP数据集上,逻辑回归模型取得了最优的性能,不过SVC模型也取得了良好的性能,并且仍远优于其他两种模型。综合考虑下来,SVC模型能够有效提升蛋白质复合物识别算法的性能。
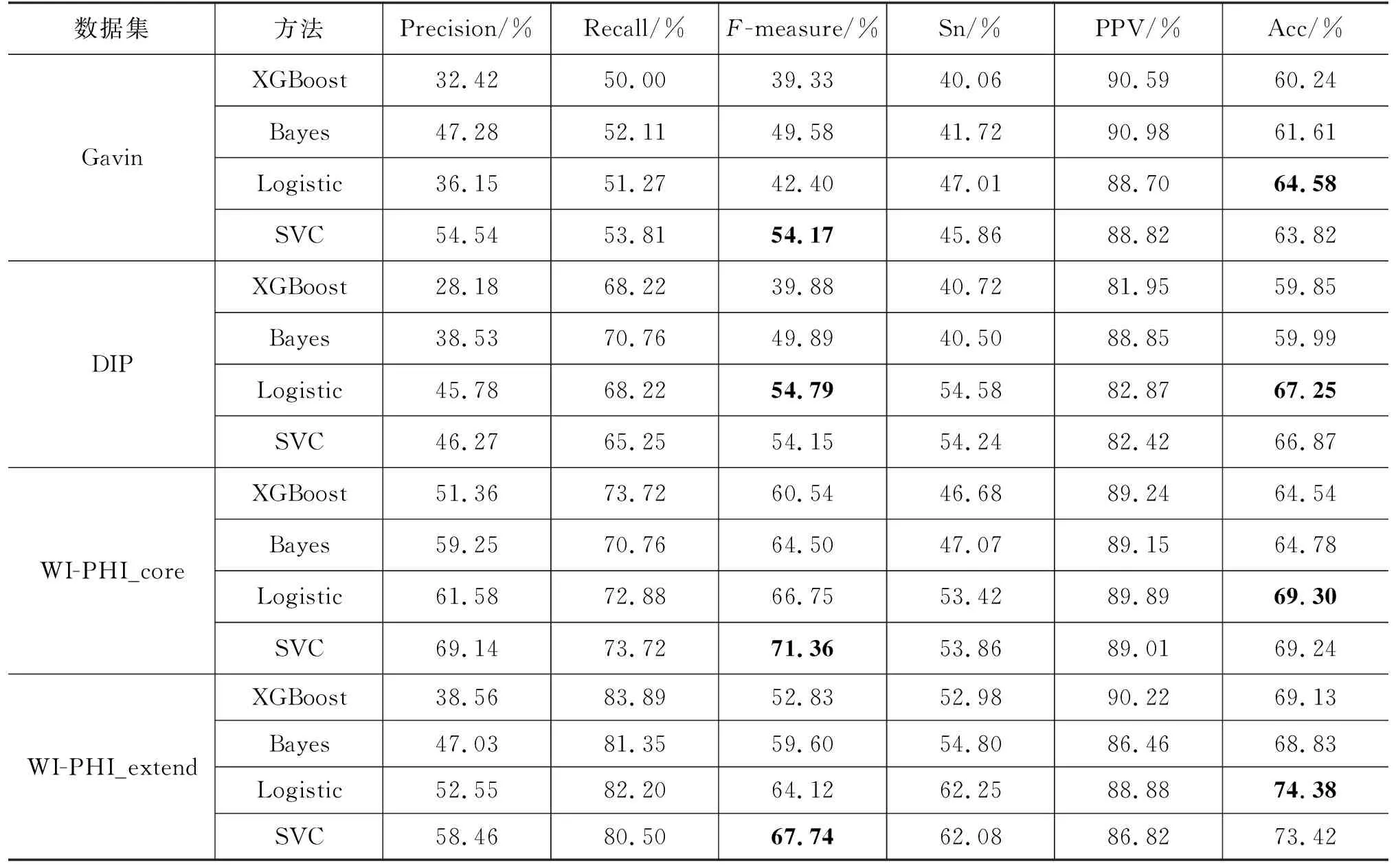
表4 SVC模型与其他监督学习模型的性能对比
3.3.2 与其他方法的比较
为了评估NOBEL方法在蛋白质复合物识别方面的有效性,我们将NOBEL方法在四个不同的PPI网络上与几种蛋白质复合物识别方法进行比较。其中,包括经典的无监督方法MCODE[2]、ClusterONE[3]、COACH[7]、CMC[6]和近几年出现的无监督方法CPredictor 2.0[9]、GANE[11],以及监督学习方法SLPC[12]。其中,MCODE和ClusterOne方法是使用Cytoscape[27]运行得到的,参数设置为默认设置,其他几个方法的参数按照它们作者的建议进行设置。NOBEL与其他蛋白质复合物识别方法比较的实验结果如表5所示。

表5 基于CYC2008与其他方法的性能对比
在Gavin数据集上,NOBEL方法在评价指标F-measure上取得了最高的性能为0.541 7,要远高于无监督方法,同时也比监督学习方法SLPC高4.39%。在DIP数据集上,NOBEL取得了最高的F-measure(54.15%)以及最高的Acc值(66.87%)。在WI-PHI_core和WI-PHI_extend两个数据集上,NOBEL同样取得了最高的F-measure,分别为71.36%和67.74%。NOBEL在四种PPI网络上都取得了最高的F-measure,而监督学习方法SLPC在所有网络上都取得了第二高的F-measure。综上所述,NOBEL方法在四个数据集上都取得了良好的性能。与现有的蛋白质复合物识别方法相比,NOBEL方法具有优越性。
3.4 讨论
3.4.1 不同参数对性能的影响
在NOBEL方法中,本文使用了SVC模型来判断子图是真实复合物的概率。在训练SVC模型时,改变SVC模型的参数会返回不同的模型。为了验证SVC模型的最佳参数,我们选用了不同的参数训练模型。图1表示不同参数的SVC模型在WI-PHI_core数据集上用F-measure测量性能的比较结果。图中C表示惩罚参数,degree表示多项式ploy函数的维度。当C=3,degree=4时,SVC模型达到了71.36%的最高F-measure。在其他三个PPI网络上,SVC模型在C=3,degree=4时也取得了优异的性能。因此,在我们的实验中选择C=3,degree=4为SVC模型的默认参数。
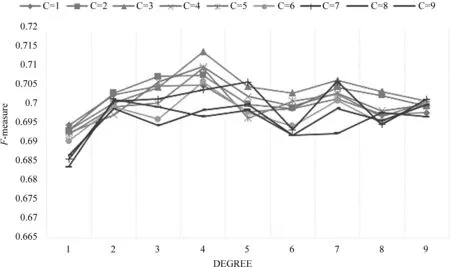
图1 在WI-PHI_core网络上应用不同参数SVC模型的性能比较
3.4.2 不同特征对性能的影响
每个特征对实验的影响是不同的,为了评价特征对实验性能的贡献,我们使用了三种不同的特征集进行试验,三种特征集分别为7个未加权特征、9个加权特征和全部的特征。表6显示了三种特征集的实验结果,从表中可以看出,加权特征集的实验结果要比无权网络特征集的实验结果好得多。另外,加权特征集的实验结果与全部特征集的实验结果相比也相差不多,这表明由加权网络提取的特征对提高实验的性能十分有效。这主要是因为我们对网络加权时,不仅结合了网络的拓扑特性,还结合了蛋白质的GO信息,这使得由加权网络提取的特征包含了蛋白质的拓扑信息和生物信息。
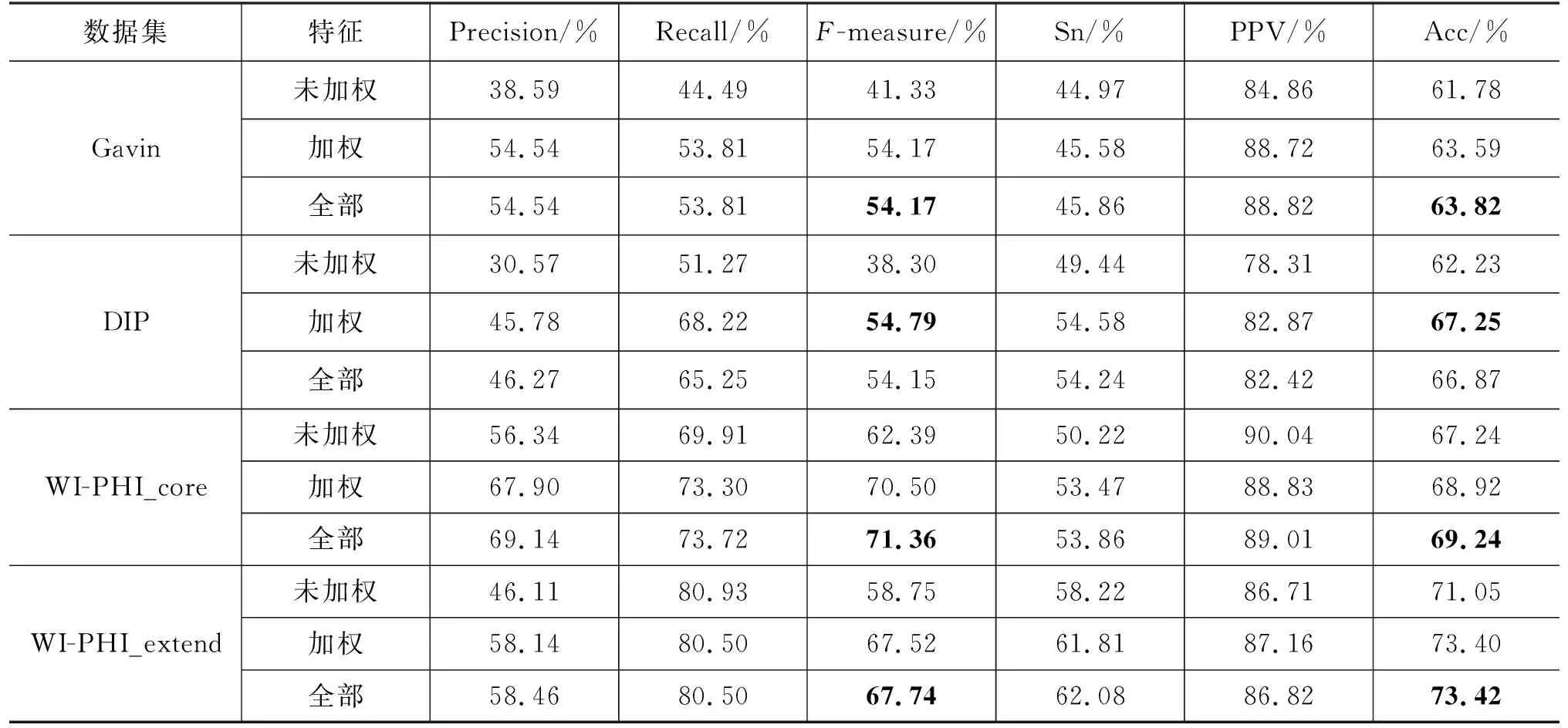
表6 不同特征集实验的性能对比
本文中,为了衡量每个特征对实验的贡献,我们用Shap[28]值来计算SVC模型中每个特征的重要性。由于训练集由正例和负例两类数据构成,Shap值计算时会同时输出两组矩阵,分别对应正例和负例两个标签,两个矩阵内的值互为相反数,结果如图2所示,其中,Class0表示正例,Calss1表示负例,x轴表示Shap值的绝对平均值,y轴表示不同的特征。Shap值也可以选择单独输出某一个标签对应的矩阵,我们选择输出正例标签对应的矩阵(图3)。从图2和图3可以看出,每个特征按重要性降序排列,而加权特征的重要性要远高于无权特征。为了验证这一想法,我们去除权重网络特征后,再次训练SVC模型并计算各个特征的Shap值(图4、图5)。由图中可以看出,去除加权特征后,无权特征在模型训练过程中也能发挥重要作用。由此可以看出,加权特征和无权特征对实验性能的提升都有贡献,只是相比无权特征,加权特征更加重要,能更加有效地提升实验性能。

图2 各个特征在SVC模型中的重要性(两标签)

图3 各个特征在SVC模型中的重要性(正例标签)

图4 去除权重特征后各个特征在SVC模型中的重要性(两标签)

图5 去除权重特征后各个特征在SVC模型中的重要性(正例标签)
4 总结
蛋白质复合物参与多种生物进程,因此蛋白质复合物识别对我们理解细胞组织和功能具有重要意义。近年来,随着技术的进步,PPI网络的规模正在快速增长,研究者提出了许多的蛋白质复合物识别算法。然而,现有的算法大多都是只基于PPI网络的拓扑信息或者利用已知蛋白质复合物信息的方法,它们都具有一定的局限性。
本文提出了一种结合已知蛋白质复合物拓扑信息和监督学习的蛋白质复合物识别算法NOBEL。首先,我们通过蛋白质的生物信息和拓扑信息对PPI网络进行加权处理;然后,我们根据加权后的PPI网络和未加权的PPI网络提取蛋白质复合物的拓扑信息作为它的特征;其次,依据丰富的特征构造训练集并训练SVC模型;最后,我们运用Clique算法搜索PPI网络中的子图作为初始子图,再通过SVC模型判断子图是真实复合物的概率来对子图进行过滤、扩张和合并操作。实验结果表明,与现有的蛋白质复合物识别方法相比,NOBEL方法拥有更优的性能。在未来工作中,我们希望能从蛋白质复合物中自动获取具有复合物信息的特征,例如,通过网络表示学习方法得到复合物的特征。
