基于K-means算法的轨迹数据热点挖掘算法

徐文进,管克航,马 越,黄海广

(1.青岛科技大学信息科学技术学院,山东 青岛 266061; 2.中国海洋大学信息科学与工程学院,山东 青岛 266100;3.温州大学计算机与人工智能学院,浙江 温州 325000)

0 引 言

海上船舶通过船舶自动识别系统(Automatic Identification System, AIS)终端和卫星终端将海量的船舶定位数据通过AIS基站、卫星通讯等方式传输至数据中心[1]。虽然中心根据数据可以简单地查找出渔船的信息，如位置、船舶的状态等，但是对于轨迹数据热点的寻找是非常欠缺的。文献[2-3]论述了渔船数据的收集和系统的开发，但是缺少了对数据的挖掘。现阶段通过渔船轨迹数据追寻捕鱼热点面临着3个迫切需要解决的重要问题。首先，海量的数据无法处理，对于渔船数据来说，每个小时的数据记录量已经达到了十几万条，这对于数据的实时处理是非常重要的；其次，选取部分数据作为研究对象缺乏依据，比如选取哪些数据可以代表一批次的渔船活动的轨迹等，数据的选取完全是人工选定，缺乏客观性；最后是热点追踪技术的研究，一般是使用热力图的方式查看热点的区域，当数据量达到几百万、几千万时，热力图的计算开销非常大，难以实现热点的定位。文献[4-5]开展了一种基于时空数据场与复杂网络的城市热点提取的研究，主要是把轨迹点与现实中的道路和区域相符合然后根据行政区域之间的时空演变来进行热点的挖掘；文献[6]开展了一种行为识别与时空分布的研究，分析了交接班事件的时空分布特征；由于渔船在海洋中行驶，并没有线路、站点、区域的划分，所以在渔船轨迹中以上的热点挖掘算法是无法实现的。回归到热点挖掘的本质，其实就是对经常活动的区域做出聚类操作。本文尝试使用K-means这种经典算法进行对渔船轨迹热点的挖掘。K-means作为一种经典的聚类算法，它是给定K值，然后随机地初始化K个中心点，计算其他点到各个中心点的距离，把该点划分到该类之下；然后进行中心点迭代。虽然随着研究的深入，对于K-means算法本身在初始化中心点以及确认K值策略上有了很大的进步，如文献[7]为了降低K-means算法对于初始化中心点的依赖性，选择K个相互距离较远的样本点作为中心点进行聚类；文献[8]运用密度指针的方式进行聚类的初始化；文献[9]提出了一种基于最近邻接距离的方式确认K值等方法。综上，改进的算法只是在小样本的数据中表现很好，对于上万条或百万条数据而言，一般的改进聚类算法都是无法满足需求。以上的改进K-means算法根据给出的数据完成聚类的操作，无法实现对数据进行处理，比如按照一定的规则选出信息价值较高的数据，然后进行聚类。对于渔船轨迹数据而言主要的问题是，数据量较大、数据具有时间维度特性，一般的改进聚类无法完成相应的聚类操作。

本文提出的热点挖掘算法，利用文献[4]中的时间序列的思想，来查看在时间间隔T下的轨迹的变化。设置置信水平系数，作为选取数据的依据，并引入KL散度作为评判数据是否具有合法性的判断，最后通过K-means聚类方法进行数据的聚类。对于原始K-means算法需要输入K值的问题，文献[9]提出了一种聚类有效性度量的方法。本文参考其处理的办法，从而整体上实现了热点定位。

1 K-means算法概述

类算法在1975年于《Clustering Algorithms》著作中论述到，它是Hartigan编写的首个关于类算法的书籍。在后来的发展中，学术界又进行了积极的探讨和挖掘，聚类分析延伸出了多种基于不同原则的聚类算法，在这其中就包含了以层级法及划分法为代表具有较好聚类效果的算法[7]。同时人们在不断的探索下，为了弥补聚类算法的缺点，提升聚类的效果，使用了其他的方法与之结合，促进了聚类算法在其他领域中的应用，比如免疫算法、遗传算法等。

K-means算法作为一种常用的聚类算法，它有聚类方法简单、效率高的特点。该算法目的是：把所有的样本分为K个不同的组，K值的确定是人工选定的。其过程是，算法根据人工设定的K值，随机初始化K个中心点。通过公式(1)，计算剩余点距离各个中心点的距离。把该样本点划分给距离最近的核心点，直至划分完所有的点。

I(i)=‖x(i)-x(j)‖2

(1)

对比查出最小的I值，将点划分到距离最小的那簇类，直至完成所有的数据点，最后运用公式(2)计算新的中心点，直到中心点不再改变时结束[9]：

(2)

K-means算法的步骤如下：

步骤1 初始化并设置K值，初始化一个S簇，其中S簇包含了所有的样本。

步骤2 在所有的样本中随机选择K个不同的值，作为算法的初始中心点。

步骤3 根据公式(1)计算剩下样本点与各个簇中心点的距离。

步骤4 遍历所有的样本，利用公式(2)更新各个簇的中心点。

步骤5 查看此次的中心点是否发生了变化，如果是则重复执行步骤3～步骤5，否则执行步骤6。

步骤6 算法结束。

根据算法的整体描述，可以看出，K-means在处理数据时，只是给出了聚类的方式[10]，不会对数据进行任何处理，而且K值需要人工设定，在渔船轨迹数据进行聚类时，发现由于轨迹数据具有时间序列性以及数据量大的特点，原始的K-menas算法无法进行有效聚类以及热点定位。本文以此为切入点，提出一种基于K-means的渔船轨迹数据热点挖掘算法。

2 基于K-means的渔船轨迹数据热点挖掘算法

在研究渔船轨迹热点捕捉的过程中，K-means算法虽然在聚类方面表现优异，但处理渔船数据这种具有时间序列性、数量大的数据时无法准确进行热点聚类。所以本文利用时间维度、KL散度和聚类有效性度量的方法来改进K-means算法,使其具有可以处理渔船轨迹数据的能力。

2.1 时间维度处理轨迹数据

为了解决渔船轨迹数据具有时序性、数据量大的问题，本文提出时间维度处理渔船轨迹数据的方法。在介绍时间维度获取数据之前，需要简述置信度、置信区间以及KL散度的概念。

在统计学中，置信度(可靠度)与置信系数多被用来判定样本选用是否合理的依据。本文简略地介绍一下关于统计值、参数值的一般概念。对于样本来说，其统计值与参数值是不同的，对于统计值来说，它是描述关于样本在某一方面特征的信息，具体而言，统计值是关于样本的某一个具体属性的均值的概念。对于参数值来说，它是对样本整体的一个具体属性真实的描述。置信度是指全体样本的参数值落到所选样本统计值区间([1-a,1+a],其中a一般取0.5)中的概率是多少。置信度是评价样本选择是否合理的重要参数值，置信区间是描述样本与整体样本之间的差异值是多少，是评价样本对于整体样本来说是否是精确的指标。KL散度是用来衡量2种数据分布之间的相似性的指标，KL计算的值越接近0，说明2种数据的分布越相似。

时间维度处理轨迹数据的思想，借用了置信度与分布相似性的思想。按照时间间隔T把具有时间序列化的数据进行切片，按照时间顺序排列数据块，依次取出数据块，与该块前面的数据作对比，取出数据块交集的部分，直到计算交集部分数据满足设定的置信度和局部最小值KL值。具体操作如图1所示。

如图1所示，渔船数据的初始化操作，首先A单元中装有所有的已经按照时间顺序排列的轨迹数据，按照时间间隔T进行切片。在初始化阶段，B单元中没有数据，如图1(b)所示，数据块直接放入B中。

如图2所示，渔船数据对比取数据操作，当初始化完成后，再从A中取出一个T间隔的数据块，与B中所有的数据作对比，交集的数据放入C中，然后将数据块Ti装入B中，直到C中的数据满足置信度与KL散度条件为止。对于渔船轨迹数据置信度的计算如下：

图2的C单元中的数据为{A1,…,Ak}，每个数据包括经度值xk和纬度值yk。则置信区间(把图2的C单元中每个数据看成图2的B单元中总体数据的参数值，根据显著水平参数设置置信区间)包括k个置信区间，分别为：

第1个置信区间为[(x1(1-α),y1(1-α))，(x1(1+α),y1(1+α))]。

…

第k个置信区间为[(xk(1-α),yk(1-α))，(xk(1+α),yk(1+α))]。

统计图2的B单元中落入置信区间的个数，其过程为：从图2的B单元中拿出数据，判断是否在图2的C单元数据的置信区间内，遍历图2的B单元中的所有数据，找出能够落入以上置信区间的数据的个数n(如果图2的B单元中的数据可以落入多个图2的C单元中的置信区间，该数据只统计一次)。

(3)

其中，N为图2的B单元中的个数，n为落入图2的C单元的置信区间内的个数，a为设置的显著水平参数。

当满足了公式(3)后，需要再满足KL散度到达局部的最小值，取数据操作才完成。其中KL的散度计算过程如下：

河谷平原孔隙潜水与地表水水力联系密切，径流条件良好，枯季多为地下水补给地表水，汛期是地表水补给地下水，上游地下径流在下游多以地表径流出现。

计算KL散度需要确定图2的C单元中数据的分布情况，利用公式(4)计算图2的C单元每个数据的分布情况：

(4)

同理计算图2的B单元中的数据分布情况为计算图2的B单元里与图2的C单元重合的那部分数据的分布情况，实际上就是交集单元的数据在并集单元里的分布情况，其公式为：

(5)

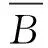
分布散度计算公式为：

D(P‖Q)=H′ (j)-H(j)

(6)

其中，D(P‖Q)代表分布散度。求出所选出的数据，分析在图2的C单元和图2的B单元中的分布情况是否相同，当数据越小时，说明B、C单元中的数据分布越相同。

通过时间维度获取数据的方法，当满足KL散度和置信度条件的时刻下，该时刻的全部数据可由其部分重要的数据代替表示。可以认为，对这一部分数据操作可以代表对全部的数据的操作。

2.2 聚类有效性度量

簇类内的距离之和值Sin的计算公式为:

(7)

簇类间的值Sout的计算公式为：

(8)

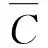
把G定义为判定聚类效果优劣程度的标准，计算公式为：

(9)

当G越小时说明聚类效果越好。使用聚类有效性度量的技术，可以实现算法自动地寻找K值，不需要人工设置，使得本文的算法更加便于使用。

2.3 本文算法流程

本文提出的基于K-means的渔船轨迹热点挖掘算法实现的具体步骤如下：

步骤1 输入总的轨迹数据，设置参数T和a，其中，T为取数据的时间间隔，a为显著水平参数，G=0、K=1。

步骤2 总的轨迹数据中每隔时间间隔T的数据构成一个数据块Si，其中，S1代表第1个时间间隔T的数据块，S2代表第2个时间间隔T的数据块，以此类推；将S1和S2这2个数据块取交集，即S1∩S2，获得交集数据存入交集单元；将S1和S2这2个数据块取并集，即S1∪S2，获得并集数据存入并集单元。

步骤3 利用交集单元中的数据获取置信区间，获取并集单元中落入置信区间的数据个数n，并集单元中总数据个数为N，判断n/N是否大于等于1-a，若不满足则执行步骤4；若满足则计算交集单元里的数据分布情况和并集单元里的数据分布情况，再计算分布散度；判断分布散度是否接近0，若满足则执行步骤5，若不满足则执行步骤4。

步骤4 取下一个时间间隔T的数据块，将下一个时间间隔T的数据块与并集单元取交集，更新交集单元；将下一个时间间隔T的数据块与并集单元取并集，更新并集单元；返回步骤3。

步骤5 将获得的交集单元中的数据作为样本点，进行K-means聚类，计算聚类有效性度量，是否小于G：如果是执行步骤6；否则执行步骤7。

步骤6 将G赋予聚类有效性度量，K=K+1,执行步骤5。

步骤7k=k-1,进行K-means聚类输出。

以上步骤是本文热点挖掘算法的整个流程，步骤1～步骤4的操作是为了从大量的数据中选出部分信息量比较高的数据。步骤5～步骤7是为了对选出来的数据进行聚类，确定热点的分类。本文算法数据流程如图3所示。

3 试验仿真

本文的数据来源于浙江省海洋与渔业局，浙江省海洋与渔业局的数据中心可以双向访问北斗卫星、海事卫星运营商并且汇集浙江省所有的AIS基站的数据[3]。本文实验首先进行数据的预处理，通过检验数据的合法性与合理性2个方面进行数据的预处理，即数据是否有缺失情况，以及经纬度是否出现很大的偏差。具体的数据格式如表1所示。

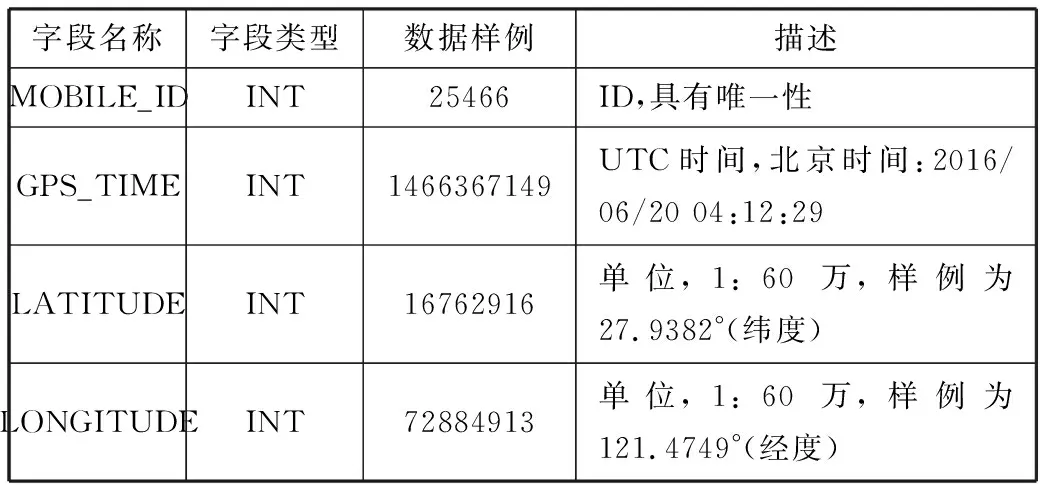
表1 数据格式

图4展示了某一天的浙江舟山渔船轨迹数据，随机选取一个经纬度的数据块作为本文算法的实验数据，本文选取了第14个区域的数据，如图4(b)所示，数据范围为经度:[124°，126°]，纬度:[30°,31°]。

实验通过与原始K-means算法的对比显示本文算法的优越性；由于热力图以特殊高亮的形式显示出访问的热点区域，所以采用热力图做参照实验来显示本文算法的正确性。

表2 本文算法设定的参数与结果表

表2为本文算法所设置的时间间隔和显著水平值以及在该设置下所达到的置信度和KL散度值。

图5所示为在00:00—03:10时段，此时渔船轨迹数据为8696条，图5(a)使用原始的K-means算法进行的聚类操作，无法聚类出热点区域。图5(b)使用热力图进行数据的展示，其中高亮的部分为渔船热点访问区域，也是捕鱼热点区域。

(a) 数据A栈的初始化 (b) 数据B栈的初始化

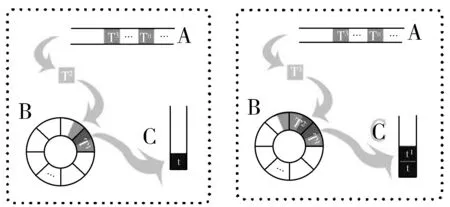
(a) 数据对比图 (b) 数据对比完成后的操作

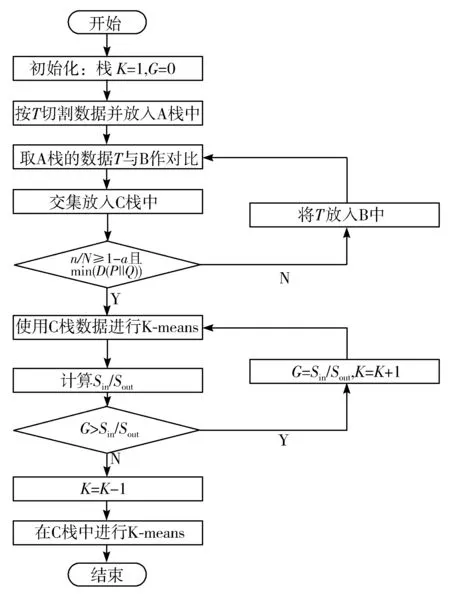
图3 本文算法流程图

(a) 渔船轨迹的可视化展示 (b) 第14区域的轨迹数据展示

(a) 原始的K-means数据进行聚类 (b) 数据的热点位置

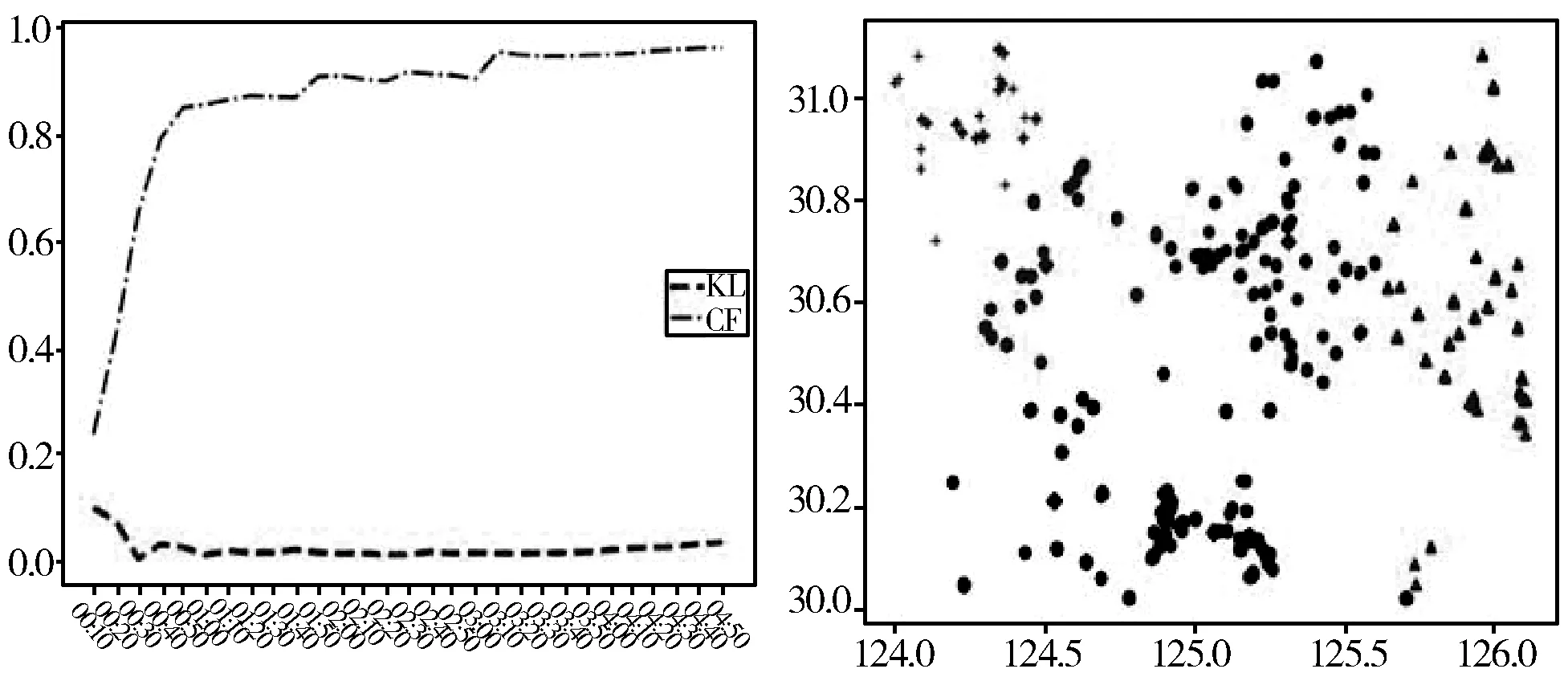
(a) 计算出的置信度与KL散度值 (b) 本文算法进行聚类

图6(a)展示了本文算法在设置参数a与T后，每个时间段下的KL值与置信度的变化，图6(b)是在03：10时，数据满足设置条件时的算法进行聚类的结果图，该图是从8696个原始数据中选出837个重要数据进行了聚类操作。通过图5(a)与图6(b)进行对比可以看出，本文算法可以有效地处理具有时序性的渔船轨迹数据；通过图5(b)与图6(b)参照实验可以看出，本文算法找出的热点形态基本符合热力图热点部分。

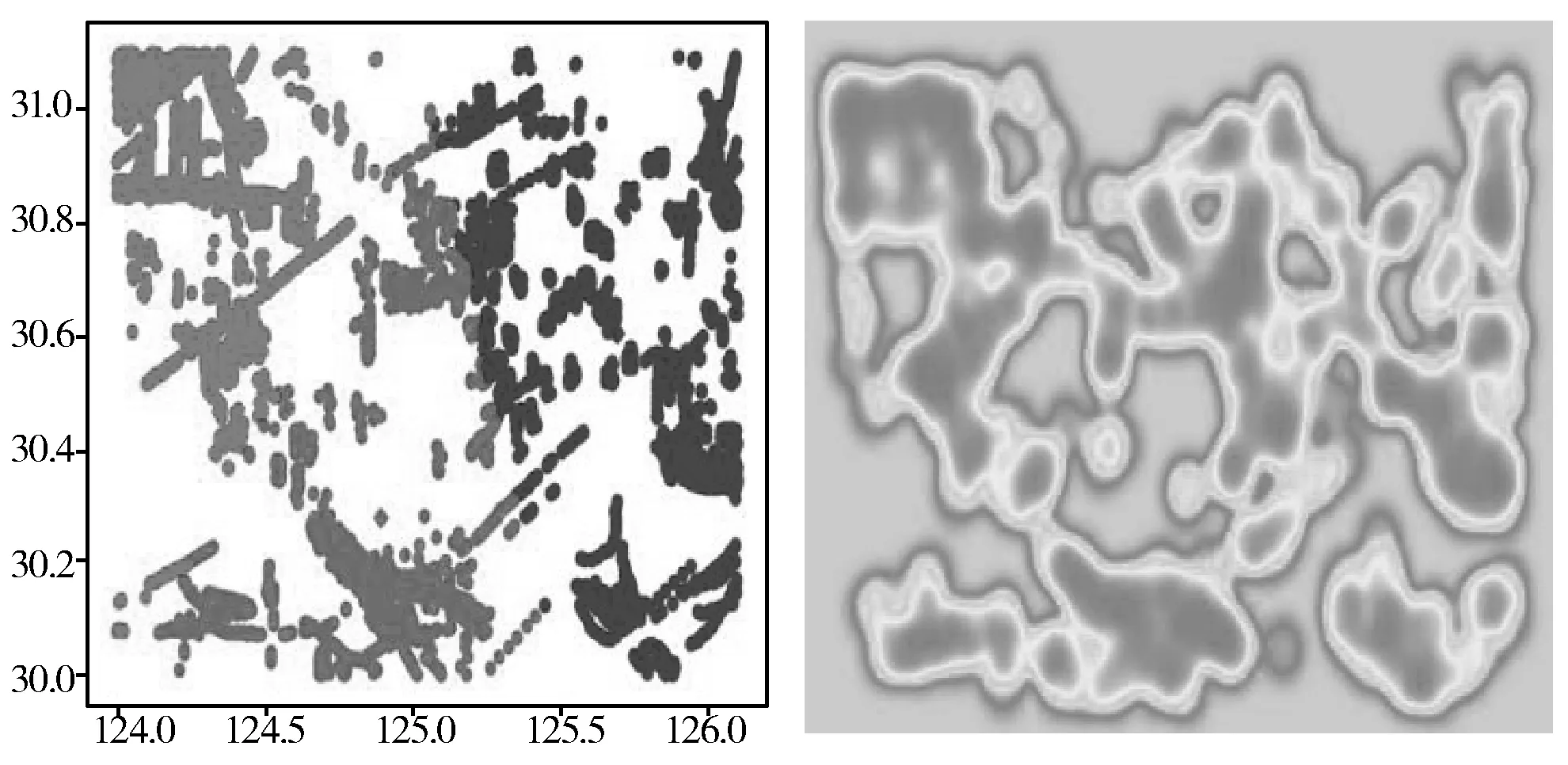
(a) 原始的K-means数据进行聚类 (b) 数据的热点位置

图7为04:00—08:40时间段下在渔船轨迹数据量为10184条时的聚类效果图，其中原始K-means算法的聚类效果如图7(a)所示，由于轨迹数据杂乱无序，无法看出该时间段的渔船轨迹热点活动区域。在图7(b)中显示了热点区域的形态。

(a) 计算出的置信度与KL散度值 (b) 本文算法进行聚类

图8(a)是本文算法[13-14]在每个时间段下的KL值与置信度的数值。当置信度满足的前提下，从出现KL第一最小值时到08:40时为止算法进行取数据操作，然后把选取的数据进行聚类操作。通过本文算法自动找寻K值发现，聚类个数为6时，聚类效果最好，如图8(b)所示。通过图7(a)与图8(b)对比可知本文算法有效地去除了无用数据，并且很好地完成了聚类操作。通过图7(b)与图8(b)参照可知，本文算法在一定程度上保证了正确性，可以很好地找出热力图中热点的位置。

表3为原始K-means算法与本文提出的算法进行对比。如表3所示，K-means算法是静态的聚类，并未对数据进行任何操作。而本文提出的算法，可以选出原始数据中信息量比较高的数据，并能根据簇内与簇间的差异值寻找合适的K值，从而完成渔船轨迹热点的挖掘工作。

表3 原始K-means与本文算法对比结果表

4 结束语

本文立足于普通的聚类算法无法满足渔船轨迹数据热点捕捉的情况下[15]，提出了一种热点挖掘算法，来自主挖掘渔船活动轨迹中的热点凸显的位置。其主要的思想是[16-18]：以置信度和KL散度为衡量标准，使用时间维度处理数据的方法，从大量杂乱的渔船轨迹数据中找出信息量比较高的数据，然后利用聚类有效性度量的方式改进K-means算法K值需要手动输入的情况[19-23]，从而实现整个轨迹数据热点捕捉。通过与原始算法的对比实验看出本文算法在处理渔船轨迹数据上的优越性，并通过与热力图参照实验说明算法在一定程度上的正确性。