弧形闸门支臂结构空间有限元分析原则研究
2021-10-19张雪才陈丽晔姚宏超王正中
张雪才,陈丽晔,姚宏超,周 伟,王正中
(1.黄河勘测规划设计研究院有限公司博士后科研工作站,河南 郑州 450003;2.黄河勘测规划设计研究院有限公司,河南 郑州 450003;3.西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100)
0 引 言
为更好地解决我国水资源的供需矛盾和水旱灾害问题,开发蕴藏的水能资源,实现变革能源产业结构,建设美丽中国的中国梦,推动我国生态文明建设,高坝大库的建设势在必行。作为高坝大库泄水建筑物调节咽喉的闸门起至关重要的作用,在水工建筑物总造价中一般占10%~30%,在江河治理工程中可达到50%以上[1],其作用是封闭水工建筑物的孔口,并能按需全部或局部开启,以调节上下游水位、泄放流量、电站运行、通航及其他控制功能。只有通过闸门的灵活启闭,才能对水库进行实时调节,满足防洪、发电和水资源调配的需要,保证水利水电工程发挥其应有的经济效益和社会效益。
随着“一带一路”沿线国家水利水电事业的发展、高坝大库的兴建和金属结构制造水平的提高,大中型和新型闸门不断涌现,其结构尺寸及承受的荷载愈来愈大,如最大孔口尺寸63 m×17.5 m的布里亚水电站弧门,最大自重720 t的白鹤滩泄洪洞弧形闸门,最高水头181 m的英古里弧形闸门,最大跨度360 m的鹿特丹新水道挡潮闸门[2]。另一方面闸门在风光水电互补和调水调沙中启闭愈加频繁,运行工况更为复杂。我国现行SL 74—2019《水利水电工程钢闸门设计规范》[3]和NB 35055—2015《水电工程钢闸门设计规范》[4]在结构选型及构件截面初选时,采用平面体系法虽具有力学概念明确、计算简便的优点,但不能完全反映真实的工作状态,有些主要构件偏于安全而有些主要构件则偏于危险[5]。因此,对这种闸门结构的分析再按平面体系法和线性理论,显得不太完善,不能充分满足闸门发展的需要。闸门在实际工作中是一个完整的空间结构体系,各构件相互协调,作用在其结构上的外力和荷载由全部组成构件共同承担,在外力作用下空间效应较强,从而使各主要构件受力复杂,这些构件不仅承受弯矩,而且还承受较大的扭矩,对抗扭刚度较小的开口或闭口的薄壁构件,由于弯矩和扭矩的作用,不仅产生弯曲应力和扭转应力,而且还因弧形闸门整体结构为高次超静定结构,从而使其承受翘曲应力,导致应力分布更加复杂。闸门结构按空间体系来分析是在前苏联符拉索夫开口薄壁杆件理论提出后才正式开始使用的,空间有限元法的快速发展使闸门结构完全按空间体系分析计算成为了现实,运用空间有限元法分析闸门结构,能充分体现闸门的空间效应,并能准确计算出各构件的应力及变形,不仅可节省材料、减轻闸门自重,同时也可提高闸门的整体安全度,空间有限元法还可作为平面体系法的一种验证方法,采用空间有限元法进行闸门结构的静力特性和动力特性分析已是基本趋势[6]。
1 闸门的有限元分析
1.1 应用现状
随着科技进步、有限元理论及相应计算软件的不断成熟与完善,诸多规范对其应用进行了明确规定。如美国《水工钢结构设计》(2014)[7]、《溢洪道弧形闸门设计》(2000)[8]和《平面闸门设计》(1997)[9]规定对闸门结构具体尺寸的确定和连接构件的分析可采用空间有限元法;我国SL 386—2007《水利水电工程边坡设计规范》[10]和DL/T 5353—2006《水电水利工程边坡设计规范》[11]规定可采用有限元进行边坡变形稳定分析及验算;SL 319—2018《混凝土重力坝设计规范》[12]和SL 282—2018《混凝土拱坝设计规范》[13]指出对于高坝和情况复杂的坝宜采用有限元进行线性和非线性分析;GB 50017—2017《钢结构设计规范》[14]规定可采用有限元法对构件、节点等进行设计;GB 50011—2010《建筑抗震设计规范》[15]规定使用时程分析法进行多遇地震下的补充计算;美国AISC 360-16《钢结构建筑规范》[16]指出采用有限元对结构进行线性和非线性分析;欧洲EN 1993-1-1《钢结构设计规范》[17]指出应采用有限元整体分析法对钢结构平面外屈曲和扭转屈曲进行分析,还有其他相关规范也都进行了明确说明。
空间有限元法在结构分析中具有完善的理论基础,实践中有迫切的需求,更容易在主观上认可和接受。从精确结构计算和安全验算来讲,采用空间有限元法进行闸门结构的静力数值分析是非常必要的,况且我国绝大多数设计单位和高校从20世纪70年代已将空间有限元法应用于闸门分析,近五十年来采用空间有限元法对闸门结构静力特性进行分析越来越普遍[18-25]。另外GB/T 33582—2017《机械产品结构有限元分析通用规则》[26]的颁布实施,商业化软件的完善与成熟,已完全具备用有限元法进行结构计算的条件,并且相对于采用传统的材料力学受力分析计算方法来说,有限元分析法可得到更加精确的结果,能解决一些采用传统力学分析时不得不做出极大简化和假设或根本计算不出来的复杂问题,如闸门动力稳定、焊缝的模拟、止水的模拟等。
1.2 分析原则的提出
尽管已有众多学者和设计人员采用各种有限元软件对不同闸门结构进行了分析,但由于不同设计人员掌握的专业知识、软件操作能力及对实际工程的理解程度不同,往往在模型简化、网格划分、边界条件、荷载施加等方面具有较大的随意性,导致即便是针对同一工程,不同设计人员会得到不同的结果,进而引起闸门设计工程师的质疑。最新出版的SL 74—2019《水利水电工程钢闸门设计规范》[3]总则中规定对于大孔口、高水头闸门宜采用有限元方法进行复核,条文说明中指出在闸门设计中,鉴于有限元分析计算过程及成果还无相关准则和判定标准,目前可作为闸门设计的重要辅助手段。NB 35055—2015《水电工程钢闸门设计规范》[4]总则中明确说明关于闸门计算体系,除了水工闸门专用的(如定轮等)作出规定外,其他一律不作硬性规定,凡未明确规定的计算方法(有限元法等),只要能准确、可靠、简便地解决结构及零部件受力问题,计算方法可酌情选择,但都没有给出明确说明及具体的使用原则,如采用何种单元、网格如何划分等。
在诸多闸门结构中,弧形闸门(见图1)以其优良特性应用最广,以往研究与事故案例[27-28]均表明失事弧形闸门中绝大多数都是由于支臂失稳导致,所以提高弧形闸门整体稳定性的关键在于对支臂结构进行精准的稳定性设计。支臂是支撑门叶结构并将其承受的荷载通过支铰传给闸墩的主要结构,屈曲问题经常发生,鉴于闸门空间有限元分析原则内容丰富、但限于篇幅,先从弧形闸门支臂结构的稳定性分析入手,对支臂结构的空间有限元分析原则进行系统探究。囿于线性有限元分析的不足,特采用结构稳定分析的双重非线性有限元法对支臂结构的稳定性进行分析,确定出支臂结构稳定设计的综合初始缺陷因数,进而为弧形闸门结构精准有限元分析奠定技术基础。
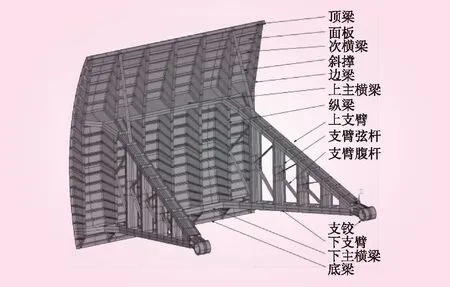
图1 弧形闸门结构
为使有限元法能在闸门支臂结构设计中有具体的规则可依据且科学高效的应用,从几何建模、网格划分、边界条件、荷载施加、分析计算、结果评价等过程进行探究,以期得到规范性的操作原则,推动有限元法在闸门支臂结构设计中安全可靠应用。制定闸门支臂结构有限元分析原则的初衷就是保证不同人员对同一闸门结构采用相同软件进行分析时具有相近或相同的结果,原则所约定的未必是最优的,但其计算结果是能保证可重复的,而能重复和追溯的结果才是可靠的。制定有限元分析原则有助于推动我国闸门设计规范颁布实施有限元分析的具体标准,提高闸门设计质量和效率,为全国乃至世界闸门结构的有限元分析评价提供安全高效的计算规则,为闸门安全运行及健康诊断修复提供理论依据,为闸门数字化设计提供有限元的技术支持,对已建闸门进行安全校核和合理评价,发现运行闸门的潜在问题,查找失事闸门事故原因等,进而保证闸门安全及整个水利枢纽和下游人民生命财产安全。所以,建立闸门有限元分析原则很必要也很迫切,应用前景广阔,经济效益巨大。
2 有限元相关理论
特征值屈曲分析的对象是理想无几何缺陷的弹性结构或构件,目的是获得结构或构件的弹性特征值屈曲荷载和屈曲模态,全面了解结构或构件的平衡分支失稳机理和弹性稳定性能。获得弹性特征值屈曲分析的意义在于,可得到考虑初始缺陷、几何和材料非线性等影响因素后实际构件临界荷载的理论上限值[29-30],对全面研究其弹塑性稳定极限承载力和工程设计具有指导意义。
实际工程中的结构总是存在几何和材料初始缺陷,且材料也不是理想弹性的,因此要确定结构或构件的弹塑性稳定性能,需要通过求解大挠度弹塑性非线性平衡方程来全过程跟踪结构效应与荷载之间的平衡路径,这一过程就是弹塑性稳定极限承载力分析。在对结构或构件进行特征值屈曲分析基础上,引入初始缺陷及几何和材料非线性,进而对结构或构件进行弹塑性稳定极限承载力分析。
3 支臂结构有限元分析原则
支臂是弧形闸门框架结构中最易发生失稳的结构。采用有限元法对其进行分析时,当单元类型和边界条件确定后,网格数成为分析结果是否准确的关键,网格数越多,数值近似解将收敛于精确解,通过增加网格数,计算精度一般会增加,但盲目增加网格数,会成倍增加网格划分及求解时间,甚至会因计算累积误差反而降低计算精度,即并不是网格数越多越好。所以,在支臂结构分析中,如何划分网格才能保证计算结果具有较高的精度,又不使计算量大幅增大,是困扰工程设计人员的难点。支臂结构分析中应根据分析目的、计算规模、效率、硬件承受能力等综合因素,确定合理的网格数,网格控制的一般原则:①网格划分应保留结构几何轮廓线,且能真实反映结构基本几何形状特征;②对结构变化大、曲率变化大、荷载变化大或不同材料连接部位应进行细化;③单元尺寸要平滑过渡,疏密网格间应有足够的单元进行过渡,避免相邻单元的质量和刚度差别过大。最后为保证计算结果的可靠性及准确性,还必须进行网格无关性验证,评估或排除模拟中网格离散误差,其基本原则是逐渐加密网格,直到再增加后计算结果不再变化。
3.1 边界条件对网格数的影响
采用有限元法对支臂结构进行分析时必须将几何模型生成有限元模型,而生成有限元模型的方法就是对几何模型进行网格划分。网格数对计算结果的影响很大,如采用一个单元时可能产生100%的误差或出现错误,采用两个单元时产生40%~60%的误差,因没有固定的网格数可以参考,一般通过网格无关性验证对有限元计算结果评价来确定合理网格数,以保证计算的经济性和准确性,所以对支臂结构进行屈曲分析时,确定合理网格数既可保证计算准确性,又可提高计算效率。
为确定边界条件对网格数的影响,选用最常用的梁单元[18-25]模拟支臂结构,对支臂截面形状(工字型、箱型和圆型)见图2、常用支臂长度(10.0~30.0 m)进行分析,并与理论计算结果对比。分析中用到的工字型、箱型和圆管截面柱均满足现行钢结构设计标准[14]的局部稳定性要求。因实际工程中支臂两端的约束情况介于固接和铰接之间,分别对两端铰接、两端固接和一端固接一端铰接的工字型截面柱进行分析。
两端铰接工字型截面柱的网格数,两端铰接情况下的截面特性及其对应的临界荷载见表1。采用有限元法对表1中的11组工字形截面柱进行稳定分析,建立的有限元模型见图2a,采用Beam 188单元进行模拟。其中两端铰接时柱长分别为10.0、12.0、14.0、16.0、18.0 m和20.0 m的临界荷载及其相应的误差与网格数之间的关系见表2。
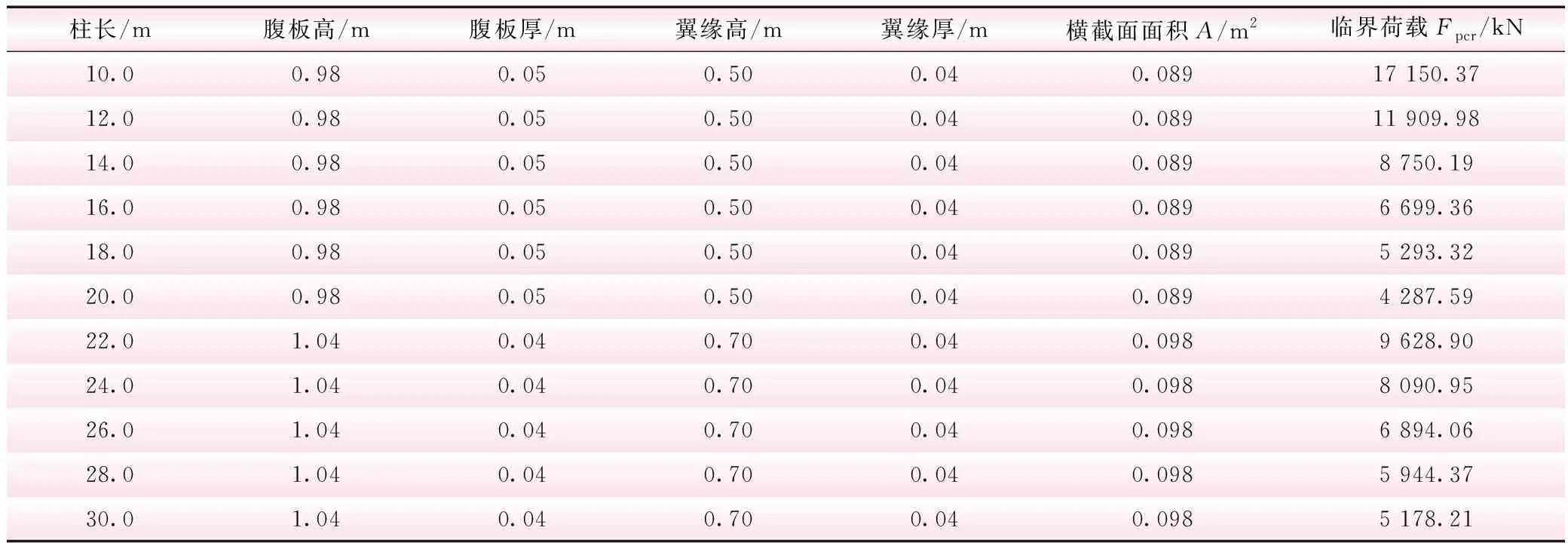
表1 两端铰接工字型截面特性及稳定临界荷载

图2 支臂截面
由表2得两端铰接工字型截面柱临界荷载误差与网格数的关系见图3。由表2和图3可知,采用有限元法对两端铰接工字型截面柱计算时,计算结果受网格数影响较大。当网格数小于4时,误差可达10%到45%;大于10时,误差仅为1%左右。综合考虑计算精度、计算经济性和实际工程的安全性,对于两端铰接工字型截面柱进行数值计算时,网格数可在10到40之间选择。分别对柱长为22.0、24.0、26.0、28.0 m和30.0 m两端铰接工字型截面柱合理网格数进行验证,网格数分别为10、20、30和40时,计算结果见表3。

表2 两端铰接工字型截面柱临界荷载与网格数
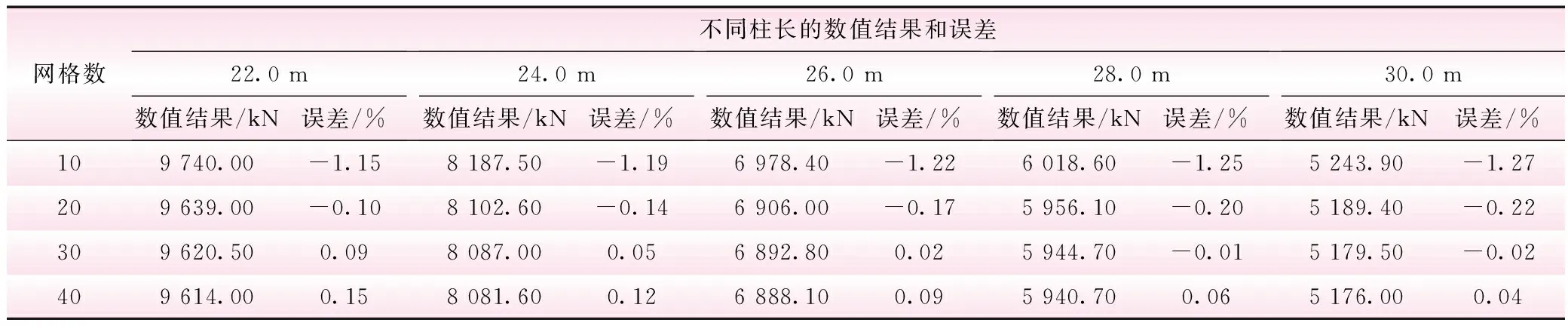
表3 两端铰接工字型截面不同柱长时临界荷载与网格数
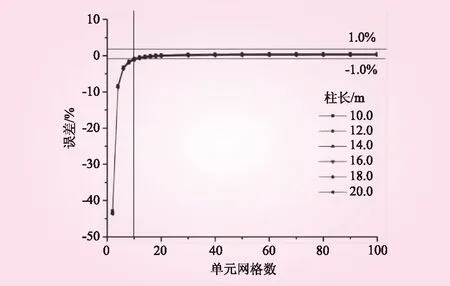
图3 两端铰接工字型截面柱临界荷载误差与网格数
由表3知,两端铰接工字型截面柱横截面尺寸和长度改变时,网格数在10到40范围,都能满足计算精度、计算效率和结构安全等要求。故对工字型的弧形闸门支臂进行数值分析时,建议网格数为10到40。同理对两端固接、一端固接一端铰接工字型截面柱进行分析,其中两端固接、一端固接一端铰接工字型截面柱截面特性及对应的临界荷载关系分别见表4和表5。
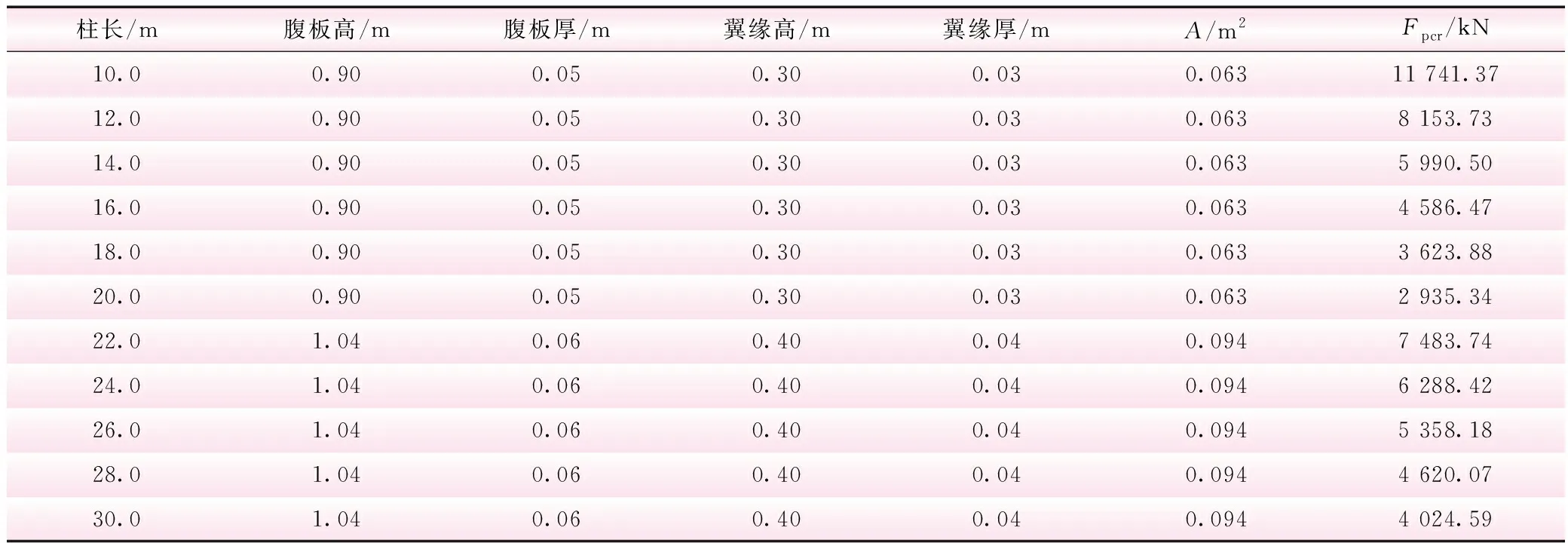
表4 两端固接工字型截面特性及临界荷载
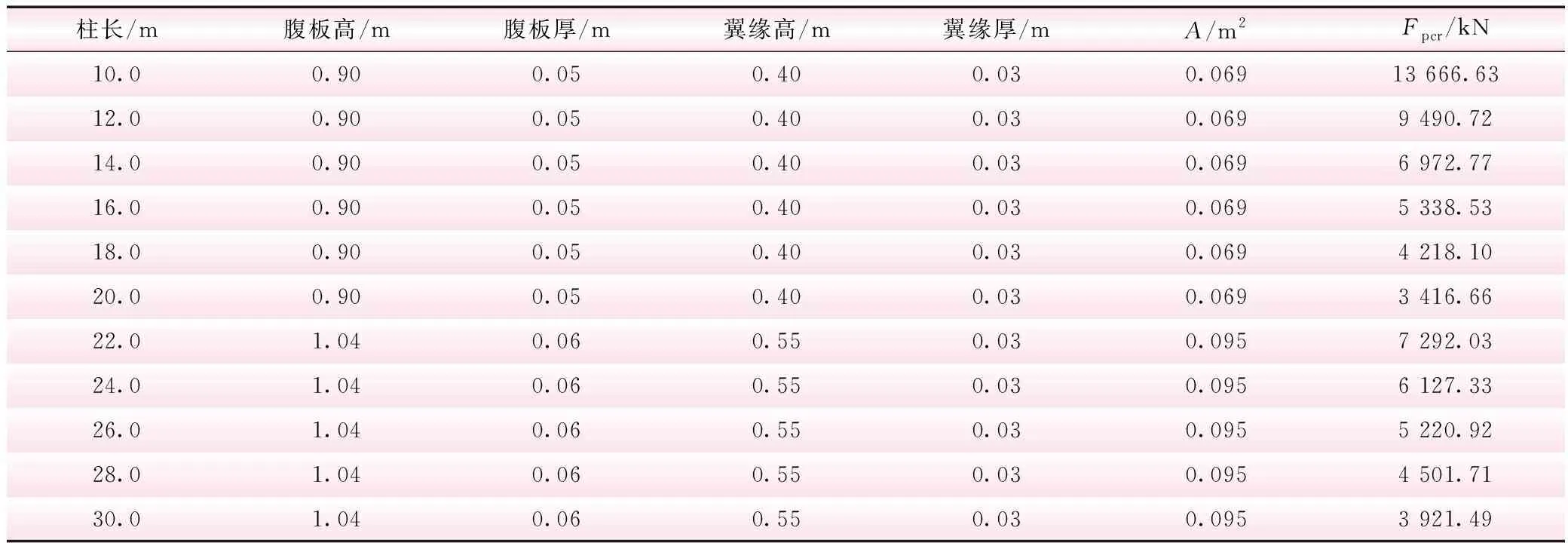
表5 一端固接一端铰接工字型截面特性及临界荷载
两端固接、一端固接一端铰接柱长分别为10.0、12.0、14.0、16.0、18.0 m和20.0 m的临界荷载及其相应的误差与网格数间的关系见表6和表7。
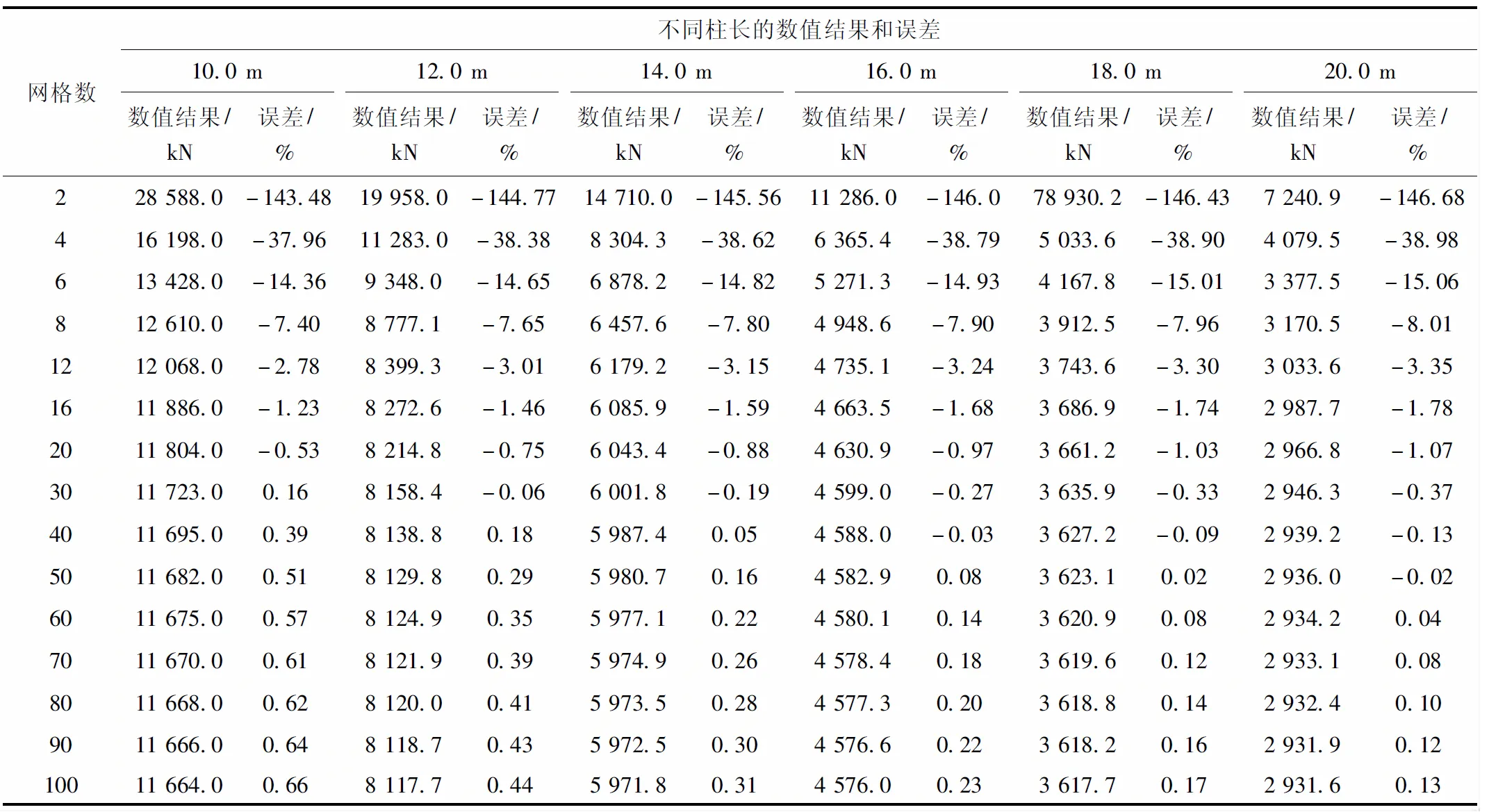
表6 两端固接工字型截面柱临界荷载与网格数
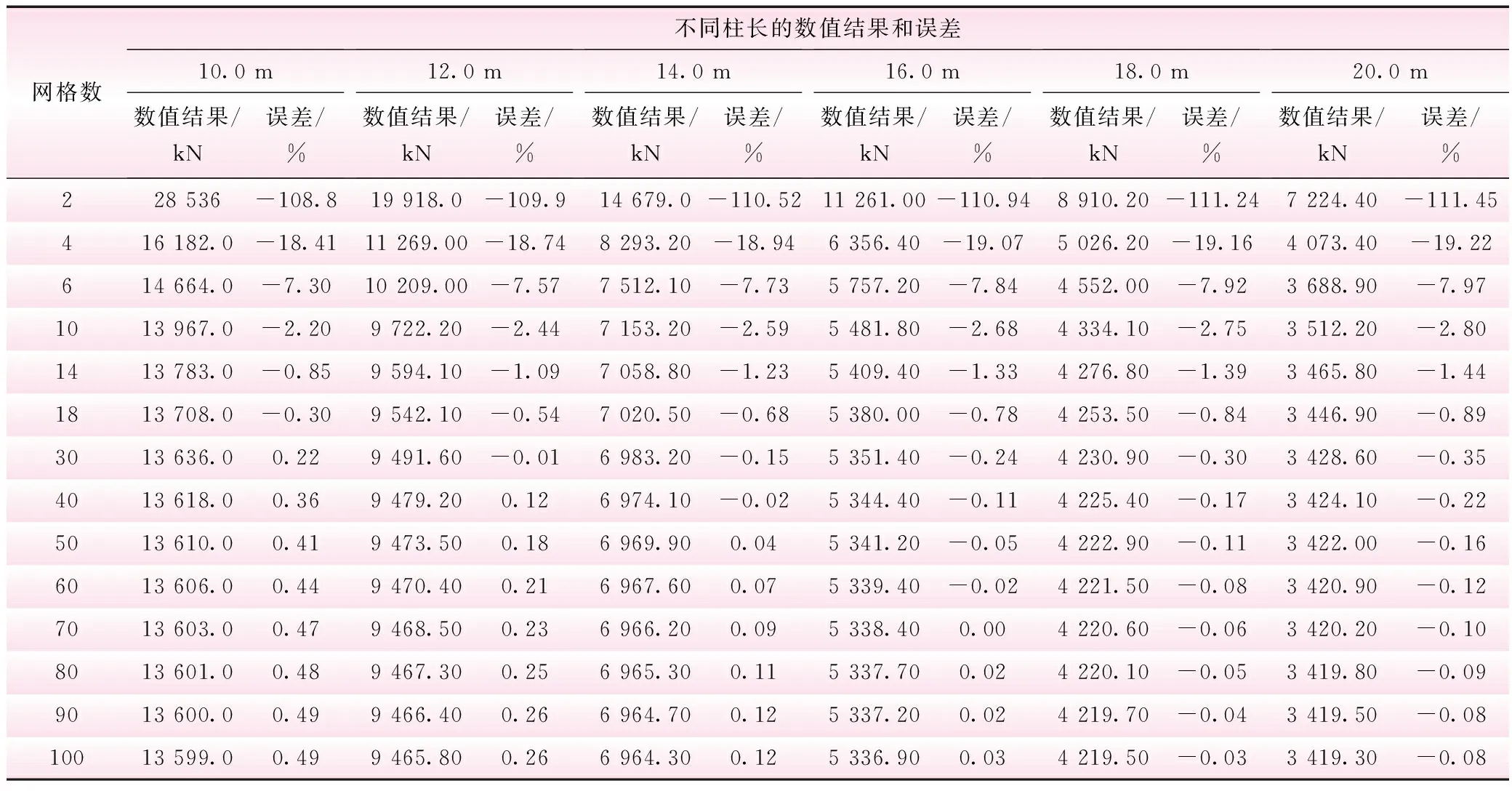
表7 一端固接一端铰接不同柱长临界荷载与网格数
由表6和表7可得到两端固接、一端固接一端铰接工字型截面柱稳定临界荷载误差与网格数的关系分别见图4和图5。

图4 两端固接时工字型截面柱临界荷载误差与网格数
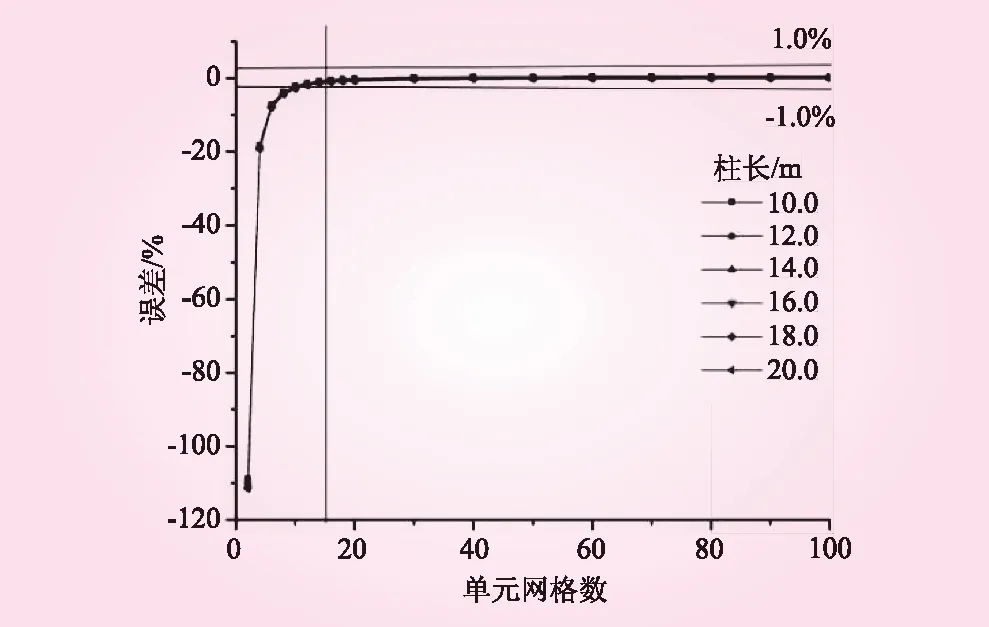
图5 一端固接一端铰接时工字型截面柱临界荷载误差与网格数
由表6和图4知,当网格数小于4时,误差可达40%到150%;大于20时,误差仅为1%。故对两端固接工字型截面柱进行数值计算时,单元网格数为20到50。分别对柱长为22.0、24.0、26.0、28.0 m和30.0 m两端固接工字型截面柱的合理单元网格数进行验证,网格数分别为20、30、40和50时,计算结果见表8。
由表8知,两端固接工字型截面柱横截面尺寸和长度改变时,网格数在20到50范围时,能满足计算精度、计算效率和结构安全等要求。故对横截面为工字型的弧形闸门支臂进行数值分析时,建议网格数为20到50。
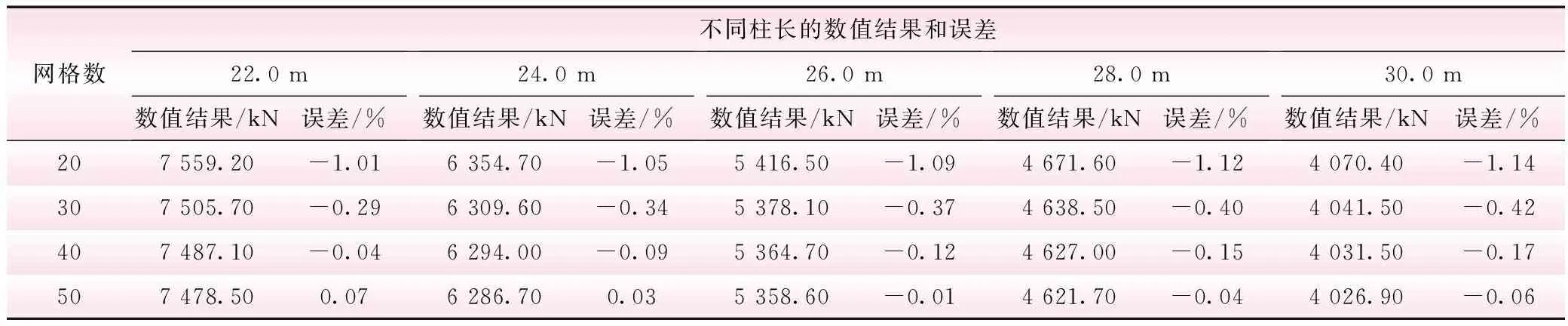
表8 两端固接不同柱长时临界荷载与网格数
由表7和图5知,当网格数小于4时,误差可达20%到110%;大于10时,误差为2%。故对一端固接一端铰接工字型截面柱进行数值计算时,网格数为16到40。分别对柱长为22.0、24.0、26.0、28.0 m和30.0 m一端固接一端铰接工字型截面柱的合理网格数进行结果验证,网格数分别为16、20、30和40,计算结果见表9。
由表9知,一端固接一端铰接工字型截面柱横截面尺寸和长度改变时,网格数为16到40时,能满足计算精度、计算效率和结构安全等要求。故对工字型支臂结构进行有限元分析时,建议网格数为16到40。
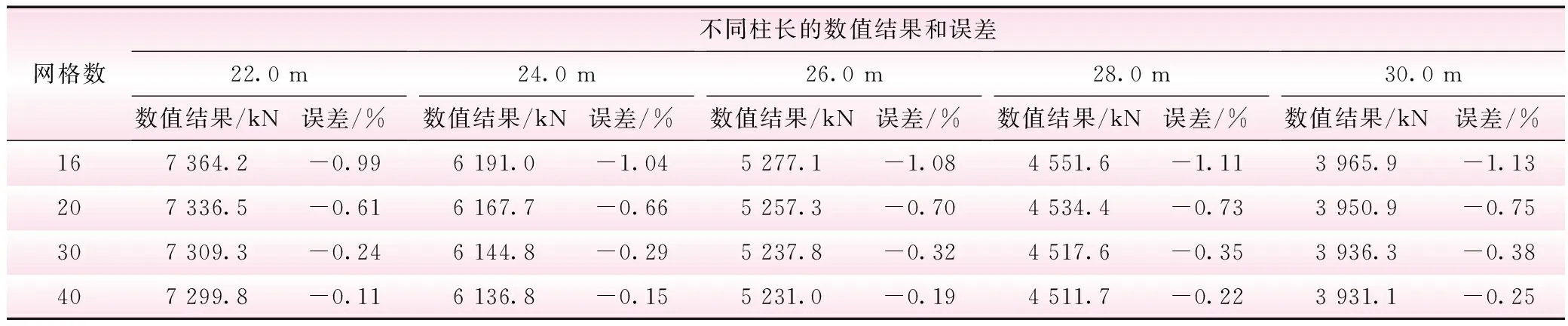
表9 一端固接一端铰接不同柱长时临界荷载与网格数
3.2 截面形状对网格数的影响
同理分别对两端铰接、两端固接、一端固接一端铰接的箱型和圆管型柱的合理网格数进行探究,具体过程同上,分析结果见表10。
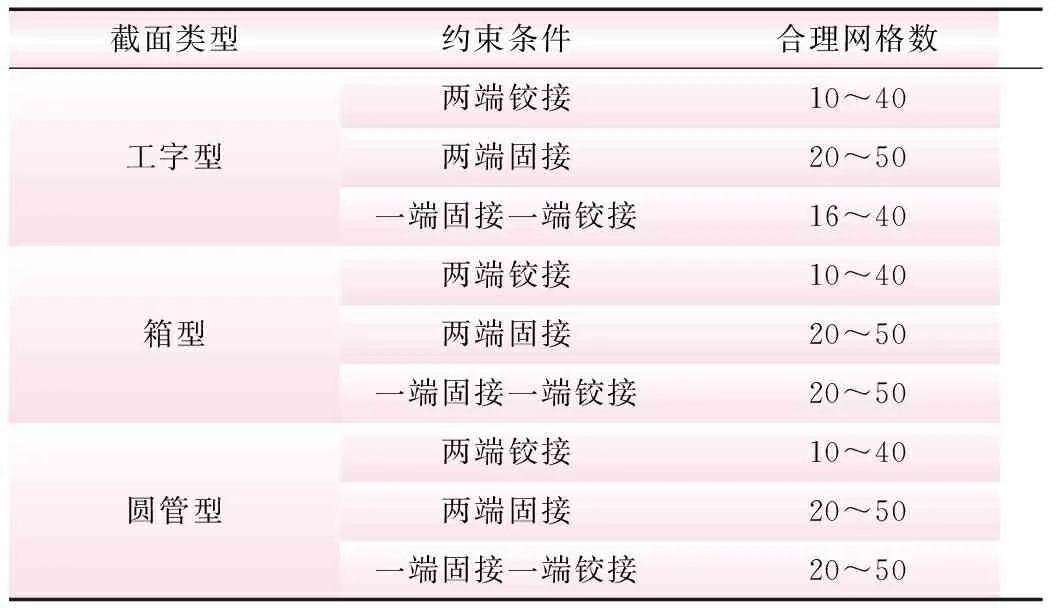
表10 合理网格数汇总
由表10可知:①对于工字型截面柱,当柱端约束不同时,合理网格数不尽相同,并且合理网格数随柱端约束的增强有增加的趋势;②对于箱型和圆管型截面柱,当柱端为铰接时,合理网格数较小,而当柱端有固接情况时,合理网格数有所增加。③当截面柱两端约束情况不同(即一端固接一端铰接)时,工字型截面柱的合理网格数较圆管型截面柱有所差别,但差别不大。
分别按现行钢结构设计规范[14]的方法和有限元法对实腹截面柱进行了对比分析,通过对实腹截面柱的不同截面型式、不同约束条件和不同柱长的对比分析发现,采用有限元法对受压或弯压构件进行分析时,采用合理的网格数,不仅可以提高计算精度,还可以提高计算效率。
4 支臂结构的稳定性计算
受压柱稳定承载力计算方法通常有现行规范法[14]和有限元法,有限元法又有线性分析和非线性分析2种。为综合对比3种计算方法的适用条件,现以等截面圆管截面柱为例进行分析,计算过程中保持圆管截面的外径D和壁厚t保持不变,仅改变柱的长度Lzb。由前文分析可知,两端铰接圆管截面柱的合理网格数为10到40,采用有限元法计算时网格数保证在10~40,圆管截面柱的特性及3种方式计算结果见表11。
表11中Fpcr-线性、Fpcr-非线性、Fpcr-规范分别表示采用线性方法、双重非线性方法和钢结构设计方法计算得到的稳定承载力,ω非线性和ω线性分别表示为Fpcr-规范和Fpcr-非线性性的误差,Fpcr-规范和Fpcr-线性的误差,由表11得柱的稳定承载力与其长细比λ的关系见图6。
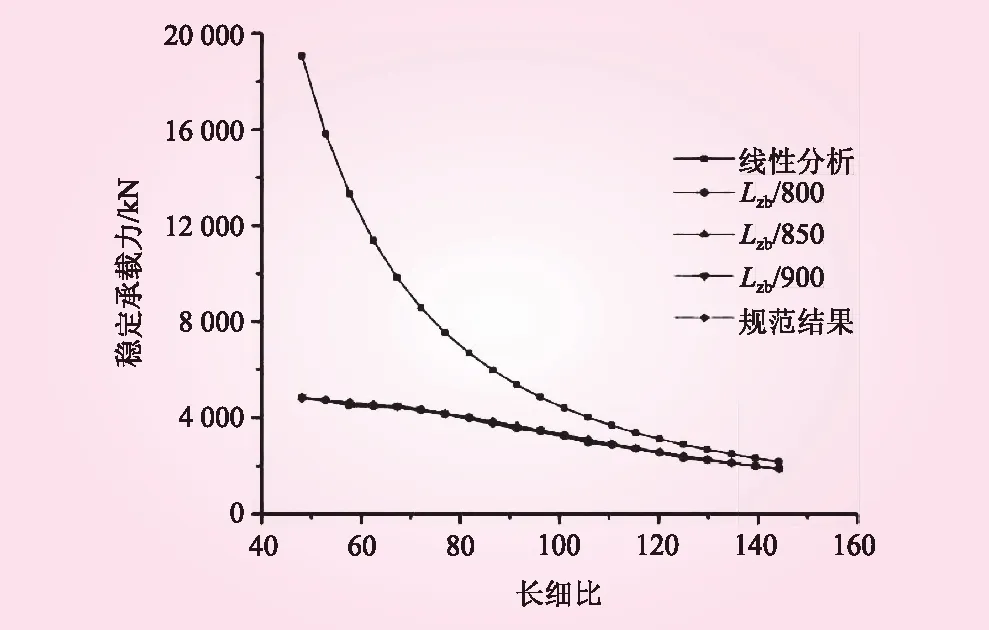
图6 稳定承载力与长细比的关系
由表11和图6知,①柱的稳定承载力随其长细比的增大而减小。②尽管线性分析和非线性分析都可以计算稳定承载力,但线性分析得到的结果都大于非线性分析结果和现行规范计算结果。③对于长细比小于101,也即中短柱,线性分析结果与现行规范计算结果的最大误差达到297.29%,当长细比大于101,也即细长柱,线性分析结果与现行规范计算结果的最大误差不超过30%。④不论中短柱亦或细长柱,非线性分析结果与规范计算结果的最大误差均不到5%,可见可采用双重非线性分析方法对其稳定承载力进行求解,且计算结果稳定可靠。⑤此外,采用非线性分析还可以对截面、约束较为复杂的情况进行高效计算,能弥补现行规范计算的局限性。⑥考虑几何与材料非线性后,构件的稳定承载力会不同程度的降低,与线性计算结果相比最大减小三倍,可知线性分析误差较大,所以对支臂进行稳定分析时要考虑其几何和材料非线性,才能确保计算结果准确可靠。
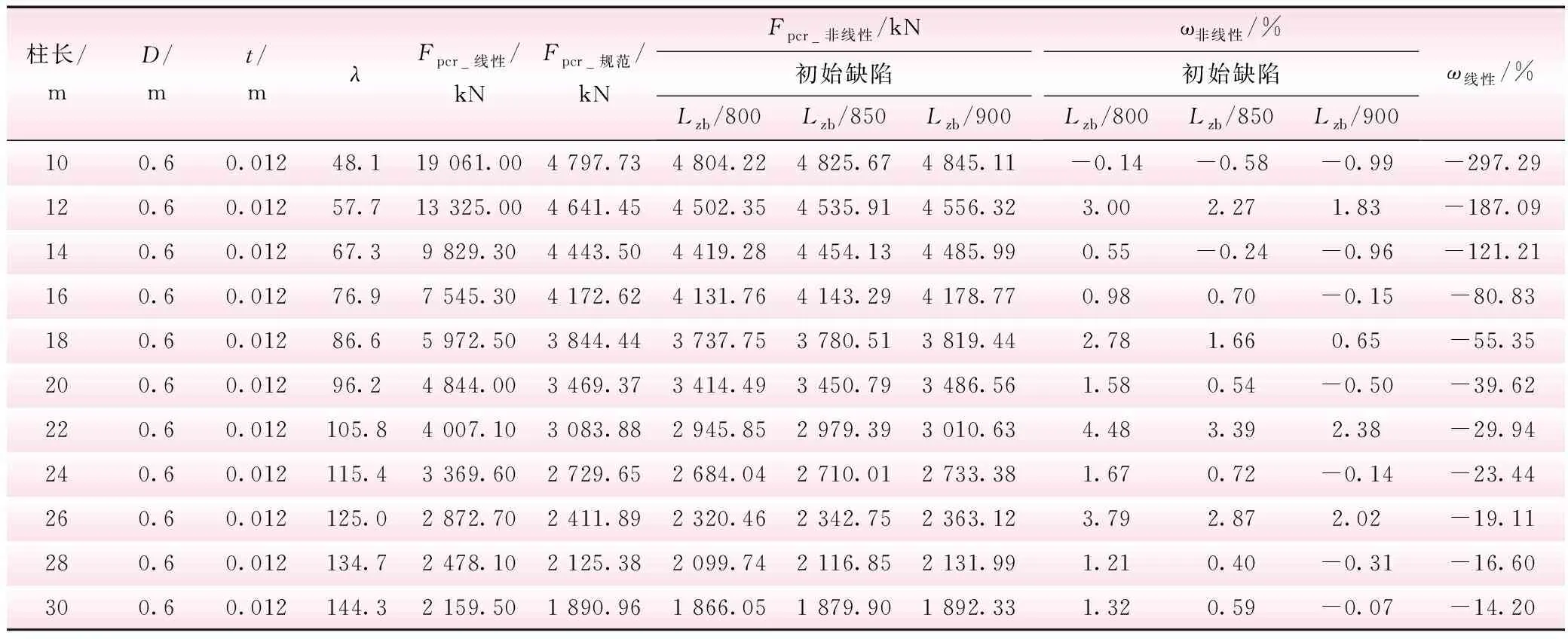
表11 截面特性及稳定承载力
5 结 论
通过对支臂结构空间有限元分析原则的系统研究,指出网格数对其计算结果至关重要,而科学合理选取网格数可保证计算经济性和精确性的统一。分析了边界条件、截面形状、网格数对支臂结构稳定性的影响,给出了支臂结构空间有限元分析的相关原则和其稳定设计的计算方法,为支臂结构精准数值分析奠定了技术基础。主要结论为:
(1)采用有限元分析时,支臂结构的截面形状、边界条件和长度等对其合理网格数影响不大,也即对支臂结构进行有限元分析时,当网格数为20到40,可满足计算精度和效率的统一。
(2)采用结构稳定分析的双重非线性有限元法对支臂分析时,对工字型等开口截面施加1/950柱长的初始缺陷,对箱型和圆管型等闭口截面施加1/850柱长的初始缺陷,得到与现行钢结构设计规范计算一致的结果,可直接对支臂结构进行稳定设计。
(3)采用结构稳定分析的双重非线性有限元法可对任意长细比的受压或弯压构件进行分析,并且得到的结果准确可靠,而线性有限元法仅能对细长杆进行分析,且分析结果偏大。
