混凝土结构动力模型破坏试验相似关系的新概念

陆 路，左春愿，孙新国，刘久涵，闫 垒

(1.淮阴工学院管理工程学院，江苏 淮安 223003；2.江苏智能工厂工程研究中心，江苏 淮安 223000；3.大连理工大学海岸和近海工程国家重点实验室，辽宁 大连 116024)

1 研究背景

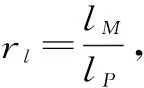
在已有的试验中可分为2种情况：一种情况是模型混凝土的抗拉强度远大于要求值，文献[6]中rl=1/350，若取(σf)P=2.0 MPa，则要求值(σf)M=2.0/350=0.005 7 MPa，但使用模型材料的(σf)M=0.30→0.70 MPa，是要求值的52.6～122.8倍，这样模型必然在较大的荷载下出现断裂，从而换算出较大的原型破坏荷载，给出偏于不安全的预报；另一种情况是模型材料的(σf)M达到要求值，如文献[7]中rl=1/300，31个模型材料的试件实测结果为0.006 MPa≤(σf)M≤0.02 MPa，结果基本满足相似要求，但由于这种极低抗拉强度模型材料的力学性能稳定性较差，在模型浇筑、风干、安装等工程中，稍有不慎，可能出现极微小的开裂，这样会导致模型试验结果的可重复性较差。文献[10]中rl=1/150， (σf)M=0.2 MPa，此时(σf)M已经是比较高的。但是2个模型试验的破坏状态有一定的差异，无论初始断裂位置，还是初始断裂的初始扩展方向都不一样。本文建议放弃rl=rσf，补充rpf=rσf的相似关系，其中，pf为初始断裂外荷载强度。

2 建议的相似关系

2.1 时间比尺rt

按弹性体运动微分方程

(1)

(2)

式中，u、v、w分别为与坐标轴X、Y、Z相应的位移；E、G、μ、ρ分别为弹性体的杨氏弹性模量、剪切弹性模量、波桑比、密度；λ称为拉梅系数；∇2为拉普拉斯算子。

根据相似理论，对于相似的运动系统，应该用相同的运动方程来描述运动状态。由于式(1)中的3个方程类同性，以下只用一个方程来代表运动微分方程，诱导相似条件。于是，描述原型和模型运动状态的微分方程分别是

(3)

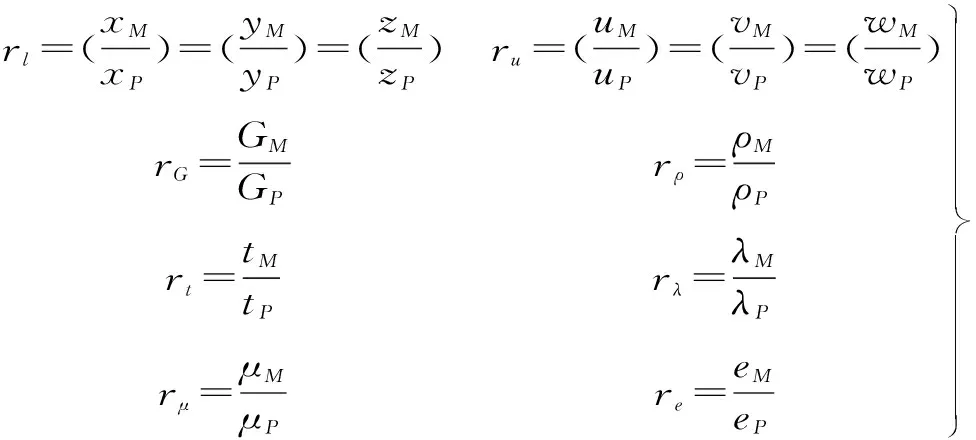
(4)

把式(4)代入式(3)第2式，则得到

(5)

假如两系统运动相似，那么方程(5)和方程(3)的第一式应该相同，即应该成为一个方程，这只有在下面2个条件成立时才有可能，即

rλ=rG

(6)

(7)

由于rλ=rG，所以rμ=1，式(6)、(7)可改写为

(8)

式(8)的第1个条件说明，为了使2个系统的运动严格相似，原型与模型材料的泊松比必须相等，这是先决的物理条件。一般以水泥为基本材料的模型材料的泊松比变化不是很大，在这变化范围内对试验结果不会有显著影响[11]。

2.2 破坏荷载p比尺

还没有精确的方程描述混凝土结构破坏后的运动过程，因此只能作简单说明。设有2柱见图1，材料分别为钢柱和混凝土柱，断面积分别为AS和AC，若在钢柱顶部作用荷载pS，混凝土柱顶部作用荷载FC，则当FS=FC，AS=AC时，两柱的应力σS=σC，和弹性模量无关。

图1 钢柱与混凝土断面应力示意

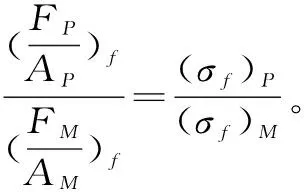
rpf=rσf

(9)

由以上叙述知，本文建议的相似关系为

(10)

进行试验时，rl、rρ、rG可以依据试验条件在一定范围内选择，rσf根据实验动力设备的功能，选择尽可能大的值。必须说明：①rt是在弹性条件下得到的，而rpf是在初始断裂条件下得到的。②初始断裂点一般为三向应力状态，因此可能出现拉裂、剪裂和压裂三种断裂状态，因此模型材料应该近似符合(rσf)Tensile=(rσf)Shear=(rσf)compressive。

3 应用算例

3.1 强冲击引起的混凝土高坝损伤试验

文献[5]对水下冲击波对混凝土重力坝损伤进行过试验研究，目的是通过模型试验预报原型防护设计的参数。假定爆心距较大，水下冲击波抵达坝址时已接近平面波，上游坝面直立，可近似认为冲击波压强在上游坝面为均匀分布。文献[5]用落锤冲击坝面(坝面与落锤不直接接触，两者之间有一水垫)，产生等效水下冲击波，当坝体出现断裂时，同时测定模型坝面的冲击压强(pf)M，从而换算得到

(11)

假设按传统的方式考虑，把rfC≠rl当作是模型制作误差，那么由试验结果换得的(pf)P为

(12)

3.2 强地震引起的混凝土高坝断裂试验

强震下混凝土高坝的断裂试验通常在振动台上进行，目的是通过试验预报高坝在多大的底面加速度时出现断裂。因此，试验时的最主要参数是振动台台面峰值加速度，关键问题是建立模型坝出现断裂时的台面加速度(af)M与原型坝体出现断裂时的地面加速度(af)P之间的关系，即确定raf。为此，作如下考虑，图2a与2b分别表示一根柱的原形和模型。

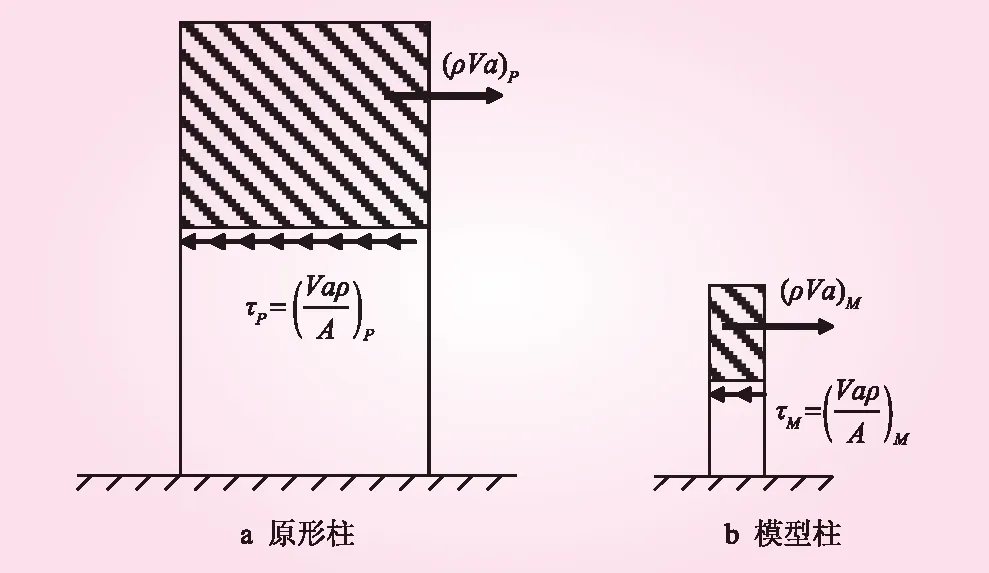
图2 原型与模型柱示意

显然，当τP=(σf)P，τM=(σf)M时，分别断裂，从而有

(13)

式中，V为阴影部分的体积；A为相应的断面积。从而有

(14)

把式(14)代入式(13)，整理得

(15)

若rσf=rl,rρ=1,那么raf=1，这就是以往常用的关系式。假设rσf≠rl，那么(aP)f≠(aM)f，若rσfrl那么raf1，即模型破坏时台面加速度(aM)f大于原型坝体断裂时的地面加速度(aP)f。但以往大多数是把rσf≠rl当作模型制造误差，这是不安全的。

4 结 论

本文建议了放弃rσf=rl的相似关系，在一定范围内自由选择(σf)M，这样便于选择模型材料、制作模型，也可以提高模型试验结果的可重复性。首次提出了破坏荷载强度比尺的概念，说明了破坏荷载强度比尺rpf=rσf。对不同的试验可取不同的破坏荷载强度，对体外爆炸引起的断裂，可取坝体表面的冲击波压强为破坏荷载强度；对于地震作用，可取地面加速度峰值作为破坏荷载强度。当rσf≠rl时，如果仍按传统关系换算原型与模型的破坏荷载强度，则会带来误差。