求解非线性方程的一类改进型牛顿迭代法
2021-10-19高寿兰
陈 伟,蔡 静,高寿兰
(湖州师范学院 理学院, 浙江 湖州 313000)
0 引 言
牛顿迭代法是求解非线性方程f(x)=0最常用的数值方法之一.牛顿迭代法的几何意义鲜明、形式简单,并在单根附近具有二阶收敛速度.但牛顿迭代法的计算过程需要调用导数值,这对函数的可导性要求很高,同时需要较大的计算量,且其局部收敛性还要求迭代的初值与精确根很靠近,这极大地限制了它的应用范围.
近年来,很多文献对牛顿迭代法做了进一步的修改与推广.文献[1]给出了经典牛顿迭代法的两种修正形式,并证明它们具有三阶收敛速度.文献[2]和[3]利用先用牛顿迭代法预估后校正的方法对牛顿迭代法进行改进,并证明其在一定条件下至少具有三阶收敛速度.文献[4]利用动力系统的李雅普诺夫方法,克服了f(x)的单调性和特殊情况f′(x)=0.文献[5]通过差商和局部指数逼近类似,构造了一类不需要计算导数值的超线性收敛指数下降迭代法.文献[6]提出一种新的二阶收敛迭代法,解决了非线性方程f(x)=0在某区间的求根和某些常微分方程的初值问题.文献[7]将Liapunov方法与指数逼近法结合,构造了一种新的二阶收敛指数迭代法.文献[8]利用割线代替切线的方法,得到了不带导数项的具有线性收敛的单点割线法和具有超线性收敛的双点割线法.文献[9]给出一种以割线代替导数,从而避免导数运算的二阶收敛迭代公式.文献[10]利用微分中值定理的渐进性和线性插值构造了一个四阶的迭代公式.文献[11]利用差商构建了一种避免导数运算的二阶收敛牛顿迭代法.文献[12]基于切比雪夫正交多项式零点插值误差的极小化性质,构造了非线性方程求根的一类迭代算法,其具有超线性收敛速度.
本文通过添加两个参数,同时对牛顿迭代法进行先预估再矫正,构造一种具有双参数的改进型牛顿迭代法.通过调整两个参数的值可以有效提高迭代法的收敛速度,且在一般情况下比牛顿迭代法具有更快的收敛速度.
1 算法构造
参照文献[4]和[8],引入一个动力系统:
(1)
其中,U(x*)为x*的某领域,μ为参数.显然,方程f(x)=0的根x*是动力系统(1)的平衡点,反之相同.
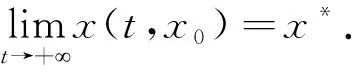
由此可见,动力系统(1)给求解方程f(x)=0提供了各种各样的可能性,采用不一样的数值方程求解动力系统(1)就能得到不一样的求解方程f(x)=0的迭代方法.
由泰勒公式(麦克劳林公式)可对函数进行如下展开:
本文将用到此公式k=-1的形式:
若利用Euler法,则可得:
xn+1=xn-hnf(xn)/[μf(xn)+f′(xn)].
(2)
在式(2)中,如果取hn=1,则可得到迭代公式:
xn+1=φ(xn),φ(x)=x-f(x)/[μf(x)+f′(x)].
(3)
当f(x)在U(x*)内有二阶连续导数时,容易得到φ(x*)=0,φ′(x*)≠0,则迭代公式(3)是平方收敛的.
在式(3)中,如果取μ=0,则可得到经典的牛顿迭代法:
(4)
文献[11]对式(4)进行了修改,构造了一种避免导数运算的迭代法:
(5)
参考上述文献的构造思想,本文对牛顿迭代法进行如下改进:
首先,利用式(3)进行预估:
最后,得到如下具有双参数的改进牛顿迭代法:
(6)
2 收敛性分析
由Euler法和传统牛顿迭代法的一些相关结论,不难证明根据式(6)改进的迭代公式在一定条件下是收敛的.因此,下面只需对迭代公式进行收敛阶的证明.

定理2设f(x):I→R在开区间I内充分光滑.如果a∈I是f(x)=0的单根,且x0充分靠近a,则由式(6)构造的具有参数的改进牛顿迭代法至少具有二阶收敛速度.
证明令
en=xn-a,ck=f(k)(a)/[k!f′(a)],k=2,3,4.
将f(x)在a处进行泰勒展开,得:
(7)
(8)
将式(7)和式(8)代入式(6),得:
整理后得:
(9)
利用泰勒公式对式(9)进行展开,只需展开到第4项,得:
即

则
(10)
由式(8)得:


(11)
将式(7)和式(11)代入式(6),得:
a+

(12)
利用泰勒公式对式(12)进行展开,只需展开到第3项,得:
即

3 数值实验
下面通过求解非线性方程f(x)=0在区间[a,b]的解,将迭代公式(3)、牛顿迭代法(4)、迭代公式(5)与本文迭代公式(6)进行比较.
例1求f(x)=4x7+x6-5x5+3x4+x3-7x2+7x-2=0在区间[0,1]内的根.
初始值取x0=0.5,终止条件为|xn+1-xn|<10-6.迭代公式(3)取μ=-1,迭代公式(5)取A=1,B=0,迭代公式(6)取λ=0.5,μ=-1.例1中4类迭代法的收敛速度比较见表1.

表1 例1中4类迭代法的收敛速度比较
例2求f(x)=2cosx-3x+3=0在区间[1,2]内的根.
初始值取x0=1.5,迭代公式(3)取μ=-1,迭代公式(5)取A=1,B=0,迭代公式(6)取λ=0.5,μ=-1,终止条件为|xn+1-xn|<10-6.例2中4类迭代法的收敛速度比较见表2.

表2 例2中4类迭代法的收敛速度比较
从例1和例2的数值结果可以看出,本文给出的迭代公式(6)的迭代结果精度明显优于其他各类修正的牛顿迭代法,且收敛速度更快.
