可变形翼导弹动态气动特性的仿真研究

丛歆雨，吴 杰

(南京航空航天大学空气动力学系，南京 210016)

0 引言

目前，飞行器对机动性、稳定性、飞行效率等提出了越来越高的要求。但是，传统固定外形飞行器的气动性能难以满足不同飞行环境和作战任务需求。从地面到临近空间，空域跨度非常大，气压、温度变化巨大，同时飞行马赫数从低速到超声速，甚至到高超声速。不同环境条件对飞行器的外形要求差异巨大，固定外形飞行器难以满足要求。在此背景下，提出了可变翼的概念。早在1903年，莱特兄弟就把可变翼的概念应用在控制飞机，那是人类对可变翼的第一次尝试。从那时开始，可变翼的研究就从未停止过。一般来说，可变翼指的是飞行器的翼面形状或其剖面形状可受控变化。可变翼一般分为翼面刚性变形和柔性变形。刚性变形如变后掠翼、伸缩翼等，可以实现机翼的大变形，已经在工程应用实践上取得较好的效果。而机翼柔性变形实现机翼的小变形，尚且存在较大的难度，距离应用还有较远的距离。对于可变翼变形的研究大多集中在飞机上，并且取得了成功的应用，如美国的F-14和俄罗斯的Tu-160，这代表了变后掠翼飞机的发展，但可变翼在战术导弹上的应用较少。

雷神(Raytheon)公司曾提出可变翼巡航导弹的方案，使其能根据飞行条件进行机翼的伸缩。Mcdaniel等研究了旋转弹翼对气动性能的影响，在不同速度下可以显著减小阻力。Bae等研究可变翼巡航导弹的气动特性，发现翼展反对称变化产生的滚转力矩可以增强横滚控制。王江华等研究了伸缩翼对巡航导弹的影响，结果显示可变翼能有效减少燃料的消耗。魏东辉等分析了变后掠翼与变展长翼对导弹气动特性的影响，揭示了导弹的变形机理。可变翼战术导弹有3方面优势：1)机动性强，可用过载大；2)作战空域广，最大射程远；3)控制品质好，容错能力强。正是上述原因，可变翼导弹具有广阔的应用前景。

可变翼在风洞实验中难以实现连续变形，因此大多是测量不同形态下的静态气动特性。为了更好地研究导弹弹翼变形过程中的性能变化，本文采用动网格技术，通过对导弹可变形收缩弹翼进行动态仿真，得到其弹翼变形过程中的连续气动性能，为后续导弹可变翼研究提供一定的参考。

1 物理模型和方程

设定导弹飞行高度为20 000 m，来流气压为5 529 Pa，来流温度为216 K，导弹简化三维模型如图1所示。导弹尾部带有6片弹翼，可以实现伸缩、变后掠等变形动作。

图1 导弹三维模型Fig.1 Three dimensional model of missile

为了保证计算网格的质量，附面层区域使用结构网格，其他区域使用非结构网格，壁面附近网格满足

y

=1，如图2所示。

图2 网格划分Fig.2 Meshing

2 控制方程

流体力学控制方程是以质量守恒、动量守恒和能量守恒为基础建立的，其中质量守恒方程为

(1)

式中，

ρ

为流体密度，

u

为

j

方向上的流体速度。在湍流情况下，动量方程为

(2)

式中，

p

为压力，

k

为湍动能，

δ

为克罗列克函数，

τ

为剪应力张量。能量方程为

(3)

式中，

E

为每个控制体内的总能量，

q

为

j

方向上的热通量，右边最后一项为由于分子扩散导致的热量传递。

上述控制方程可以使用有限体积法进行求解，它从积分守恒形式出发，对控制单元进行离散，形成间断解的黎曼问题。有限体积法既能适应复杂几何求解域，也能直接和充分利用有限差分的许多格式和概念。其次，有限体积法在每个控制体内满足守恒原理，对于整个计算域同样满足。

为了精确地模拟湍流流动，采用了SST

k

-

ω

湍流模型。SST

k

-

ω

两方程湍流模型是由标准

k

-

ε

模型和标准

k

-

ω

模型通过混合函数结合得到的。它不仅继承了两者的优点，也摒弃了两者所具有的缺陷，在近壁区和自由剪切层表现了优良的数值特性；通过改进湍流黏性系数，SST

k

-

ω

模型对高逆压梯度的流动区域具有更好的模拟能力。本文采用Ansys Fluent 19.0实现数值模拟。

3 正确性验证

采用HB-2模型(Hypervelocity Ballistic model 2)对数值模拟方法进行准确性验证，模型如图3所示。图4给出了不同马赫数(

Ma

)、不同攻角(

α

)下的轴向力、法向力和俯仰力矩系数的数值模拟结果。由图可知，本文的计算结果与实验结果符合良好，验证了数值仿真方法的正确性。

图3 HB-2模型示意图Fig.3 Schematic diagram of HB-2 model

图4 数值模拟结果与实验结果对比Fig.4 The numerical simulation results compared with experimental results

4 计算结果及分析

为了研究展弦比变化对导弹气动性能的影响规律，本文选取典型的导弹以固定攻角10°、马赫数1.5状态飞行。首先计算固定外形气动性能，此时弹翼展弦比为2.5，保持弹翼弦长不变，弹翼收缩，改变的是弹翼的展长;然后计算不同收缩速率下气动性能变化。这里定义参数

C

来描述收缩速度

(4)

式中,Δ

λ

为展弦比变化量，

t

为时间。计算

C

=3

.

75，2

.

5和1

.

25 这3种情况，分别为快速、中速和慢速3种状态。弹翼的展弦比从最开始的2.5收缩至最终的展弦比分别为1，1.5和2。展弦比随时间变化如图5所示，在0～0.4 s内，弹翼展弦比随时间线性减小；在0.4～0.6 s内，弹翼展弦比保持不变。

图5 展弦比随时间变化图Fig.5 Aspect ratio versus time

定义升力系数

C

、阻力系数

C

和力矩系数

C

为

(5)

(6)

(7)

式中，

L

，

D

，

M

分别为升力、阻力和俯仰力矩，

ρ

为来流密度，

v

为来流速度，

S

为参考面积，一般选取弹体的横截面积，

l

为参考长度，一般选取弹体的半径。在之后

C

，

C

，

C

的计算过程中，

ρ

，

v

，

S

和

l

保持不变。

图6和图7为不同飞行状态下导弹弹翼收缩过程中的阻力系数和升力系数随时间的变化曲线。可以看出，阻力系数和升力系数在弹翼收缩过程中随时间是线性变化的，它们随着展弦比的减小而减小。不同收缩速率下升力和阻力系数减小的速率也不一样，具体表现为弹翼收缩速率越快，升力和阻力系数减小地越快。当弹翼停止收缩后，阻力系数和升力系数也几乎保持不变，处于稳定状态。

图6 阻力系数Fig.6 Drag coefficient

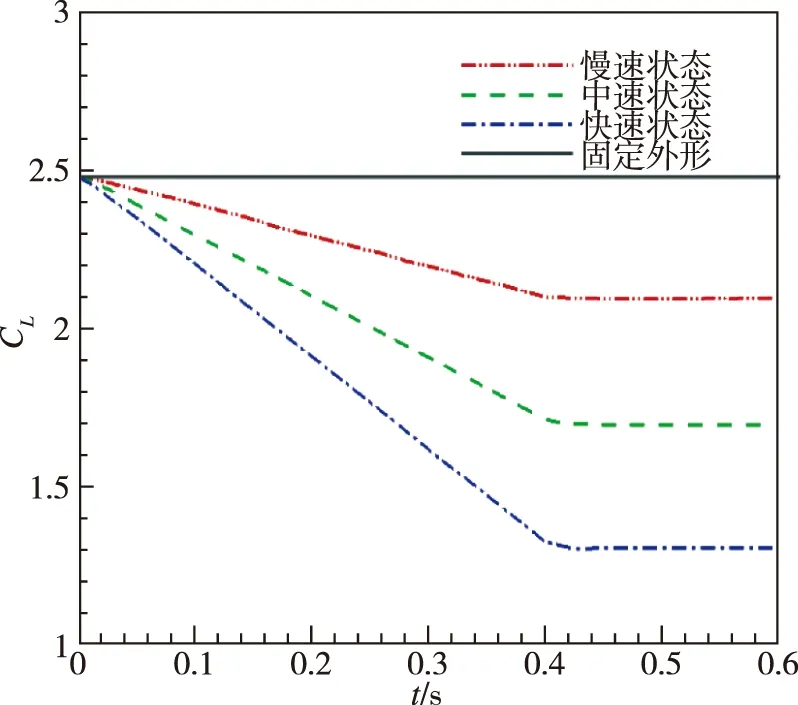
图7 升力系数Fig.7 Lift coefficient

和主要由摩擦阻力影响的亚声速阻力不同，超声速阻力主要由激波阻力决定。由图8和9可知，在弹头和弹尾弹翼部分形成了两道激波，这是导弹产生阻力的主要原因。减小展弦比则是减小激波阻力的方法之一。阻力系数随展弦比的减小而减小，对于阻力系数的减小，从图8和9的压强云图可以看出，主要是由于翼面的阻力减小，变形前后弹翼前后压强影响的区域面积减小，前后总压差减小，使得整体的阻力减小。如图10所示，慢速状态下翼面的升力系数

C

和阻力系数

C

变形前(

t

=0 s)分别为1.475和1.488，变形后(

t

=0.4 s)分别为1.106和1.158。3种模式下，展弦比从2.5到2,1.5和1，整体的阻力分别下降了13%，26%和38%。

图8 变形前压强云图Fig.8 Pressure contours before deformation

图9 变形后压强云图Fig.9 Pressure contours after deformation

图10 慢速状态下翼面变形过程中升阻力系数变化曲线Fig.10 Lift and drag coefficient during wing deformation in slow mode

弹翼在收缩过程中，对应的升力会减小。主要由两个原因引起，一是弹翼展弦比的减小，二是弹翼有效面积的减小。3种模式下升力降低了16%，32%和47%。图11和12分别为变形前压力云图和变形后弹尾的压强云图。可以看出，变形前后导弹尾部上下方压强影响区域减小，使得尾部上下总压差减小，升力减小，这是导弹在变形过程中升力逐渐减小的原因。但在超声速状态下，阻力的减小显然比升力更加重要，这也是为什么大多数超声速飞行器都采用小展弦比和大后掠角的原因。

图11 变形前弹尾压强云图Fig.11 Pressure contour around missile tail before deformation

图12 变形后弹尾压强云图Fig.12 Pressure contour around missile tail after deformation

此外，由图13可以看出，与固定的弹翼相比，力矩系数在弹翼收缩的过程中持续不断地变化，但变化量都比较小。弹翼缩减速度对力矩系数影响并不是很明显。

图13 力矩系数Fig.13 Moment coefficient

图14和15为变形前后的马赫数云图。由图可知，弹头区域的流速基本保持不变，流速主要是在弹翼前后的区域发生了变化。图中红色部分代表流速较大的区域，主要出现在导弹头部与弹身连接处、弹翼后方局部区域。这是由于在这些区域内，导弹的外形存在扩张角，气体沿流向经历膨胀，从而产生了膨胀波。由可压缩流动理论可知，膨胀波之后气流的压强、温度、密度减小，流速增加。同时，蓝色部分代表流速较小的区域，主要出现在导弹弹头的前方、导弹弹翼的前方和尾流区。弹头和弹翼前方区域流速降低是因为气流通过激波，压强、温度和密度增加，而流速降低。超声速流动在弹体底部后面发生分离，在底部形成回流区，流动在此急剧转向，形成低压区和强膨胀波。在弹体尾部拐角处，流动急速膨胀，由于尾部处位于膨胀波的影响区域内，其压力较低，这种压差是形成尾部阻力的根源。此处的低压区和周围的高压区相互作用，气流在此处由于压差的原因发生旋转，产生分离涡。如图8和9所示，由于导弹有攻角，尾部产生的分离涡是不对称的。

图14 变形前马赫数云图Fig.14 Mach contour before deformation

图15 变形后马赫数云图Fig.15 Mach contour after deformation

由上述分析可知，在低马赫数时采用大展弦比弹翼、高马赫数时采用小展弦比弹翼，可以明显地减小阻力、增加射程。导弹在弹翼变形前后周围流场的压强、速度和温度也随弹翼展弦比的变化而发生变化。不同弹翼缩减速率对阻力系数和升力系数的影响也不同。

5 结论

可变翼导弹相比固定外形导弹更适用于不同的飞行环境和作战任务，具有广阔的应用前景。伸缩翼改变了翼面面积和展弦比，弹翼伸长时具有高升阻比，弹翼收缩可以减小高马赫数飞行时产生的激波阻力。本文通过数值模拟，给出了非定常状态下弹翼不同缩减速率对阻力系数、升力系数和力矩系数的影响规律，分析了变形前后压强、速度和温度的变化，揭示了升力系数和阻力系数随弹翼缩减速率线性变化的规律,为后续的可变翼导弹深入研究提供一定的参考。