一种非线性闭环多约束最优末制导律研究

王 智, 王 鹏, 宋剑爽, 熊 伟, 洪 蓓

( 北京宇航系统工程研究所,北京 100076)

0 引言

在进行飞行器末制导律设计时，不但要保证飞行器具有较小的脱靶量，同时还需要满足一定的落角要求。在现代精确制导理念中，单纯考虑落点和落角等终端约束是不够的，还应该进一步考虑过程约束控制条件，如飞行过载、导引头视场角等条件。因此,研究复杂环境多约束条件下便于应用的末制导律具有重要的现实意义。

纯比例导引律由于结构简单，需要的制导参数少，得到了广泛应用，但是它无法很好地处理带落角约束的末制导问题。虽然偏置比例导引律能够处理带落角约束的末制导问题，但是它没有考虑动力学问题，对多约束条件下的末制导问题也很难处理。基于最优控制理论的导引律能够考虑飞行器的动力学问题，并可以考虑制导过程起点和终点的约束条件或者其他约束条件，并根据给出的性能指标寻求最优制导律。

明宝印等设计了一种最优和比例导引复合制导律，飞行末端落角接近-90°，但落角不能实现任意设定。花文华等基于零和微分对策原理设计了一种带落角约束的线性二次型微分对策制导律，其形式不受目标机动能力和形式的限制，但需要对目标的机动能力进行假设。尹永鑫等设计了滑模变结构制导律，对姿态角有较强的约束能力，能有效满足落角约束，但参数设定较难。本文基于最优控制理论，在考虑落点位置及落角等终端约束和飞行过载及视场角等过程约束的条件下，得到了便于应用的最优制导律。在建立飞行过载和导引头视角解析表达式的基础上，设计了同时考虑过程约束和终端约束的制导参数策略。

1 约束最优末制导方法建模

1.1 制导律建模

针对多约束末制导问题，基于如下假设建立制导模型：

1)飞行器和目标均按质点运动模型考虑，且均在纵向平面内运动；

2)飞行器制导系统无动力学滞后。

末制导段弹目相对运动关系如图1所示。

X

OY

为惯性坐标系，

θ

为速度倾角，

q

为弹目视线角，

R

为弹目距，

V

为飞行器速度，

V

为飞行器与目标间的相对速度，

q

为飞行器末端期望落角，

a

为飞行器法向过载指令，

ε

为初始速度指向误差角。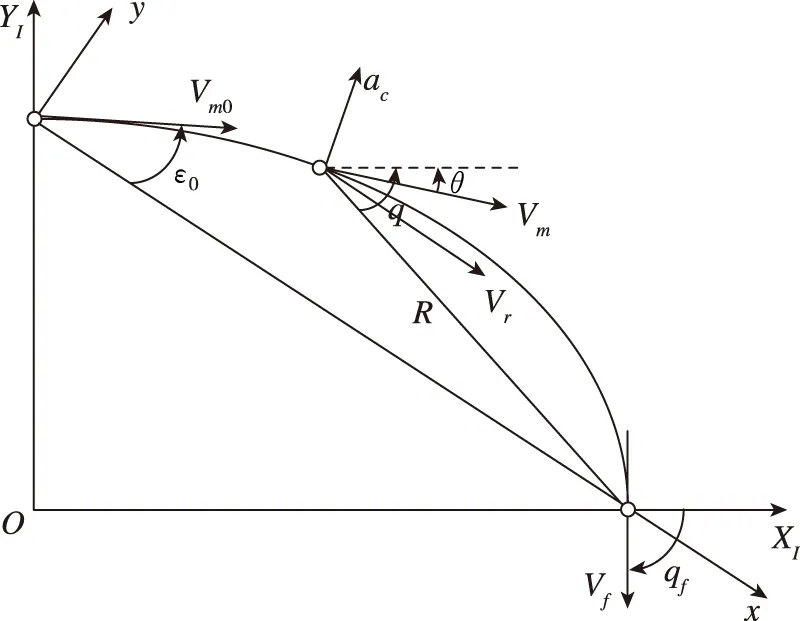

图1 弹目相对运动关系Fig.1 The relative motion relationship between flight vehicle and target

为简化制导律推导，认为

V

在初始弹目视线方向上的投影

V

为常值，则飞行器末制导段的制导问题可简化为初始弹目线坐标系下的线性制导问题。该制导问题的飞行器状态空间方程为

(1)

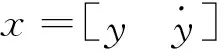
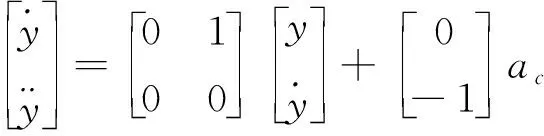
(2)

(3)

当飞行器处于飞行末端时，期望过载指令趋近于零，从而间接保证飞行器末端攻角为零。基于上述考虑，引入新的控制权矩阵(

t

)，其为剩余飞行时间

t

的函数，即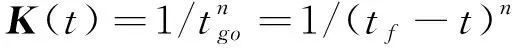

(4)

式中，

n

为制导阶次,

t

为末制导时间,

t

为当前飞行时间。

性能函数为

(5)

式中，为罚函数矩阵，为

(6)

根据性能函数可得目标函数为

(7)

要使得目标函数为最小，即要求

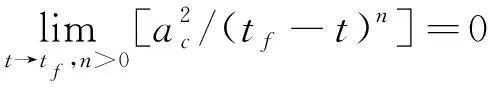
(8)

根据最优控制理论，以飞行器末制导初始时刻为起点，上述状态空间方程在终端时刻的状态量可表达为

(9)

定义函数

(10)

同时考虑终端位置和法向速度约束，式(9)可简化为

(11)

引入中间变量

η

，并应用Schwartz不等式定理可得

(12)

进一步简化可得

(13)

要使式(13)成立，则目标函数的最小值为

(14)

(15)

根据Schwartz不等式定理，过载指令为

a

(

λ

)=

I

[

h

-

ηh

](

t

-

λ

)

(16)

式中，

I

为不确定参数，期望存在最优

η

使得

Γ

最小，故d

Γ/

d

η

=0。根据式(14)，则有

(17)

将式(16)代入式(14)，则有

(18)

进一步可得飞行器过载指令表达式为

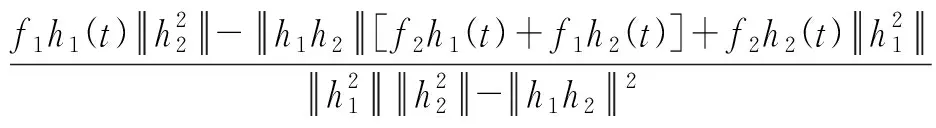
(19)

在不同时刻

t

，存在

(20)

将式(20)代入式(14)，有飞行器过载指令为

(21)

1.2 制导律简化

式(21)给出的多约束最优末制导律包含飞行器法向位移和法向速度等状态量，而上述状态量在飞行过程中很难直接测量，因此需要对制导律进行相应简化，以得到便于应用的表达式。

弹目视线角

q

(

t

)可由导引头测量得到，当

q

(

t

)为一小量时，有

q

(

t

)=tan

q

(

t

)=-

y

(

t

)

/R

=-

y

(

t

)

/

(

t

V

)

(22)

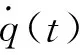
(23)

由式(22)和式(23)可得

(24)

将式(24)代入式(21)有

(25)

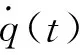
2 考虑飞行过载和导引头视角约束的制导参数设计

多约束最优末制导律作为闭环制导律可直接满足飞行器终端位置、终端落角约束，但飞行过程中的过载、导引头视角等约束无法直接进行控制。因此,研究飞行过载、导引头视角与多约束最优末制导律制导参数之间的解析特性，通过制导参数的设计，可在满足终端位置、落角等约束的同时，满足飞行过载和导引头视角等过程约束。

2.1 飞行过载解析表达式

在小角度假设下，有

(26)

在末制导初始时刻，据式(10)有

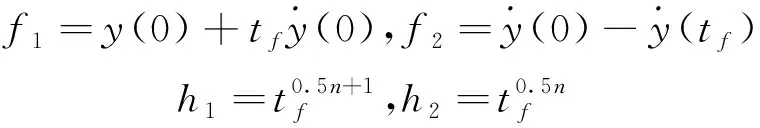
(27)

进一步由式(15)可得

(28)

将式(28)代入式(19)中有

a

(

t

)=

A

ε

+

B

q

(29)

其中

(30)

由式(29)可见，多约束最优末制导律由两部分组成，由

ε

引起的需用过载和

q

引起的需用过载。定义角度比例因子

k

为

k

=

ε

/q

(31)

将式(31)代入式(29)有

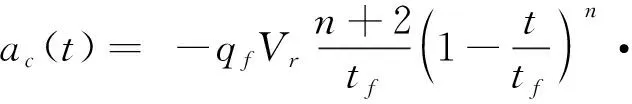
(32)

式(32)即为末制导过程中飞行过载的解析表达式。当已知

ε

,

q

,

n

和

t

时，便可求得任意时刻的飞行过载大小。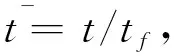

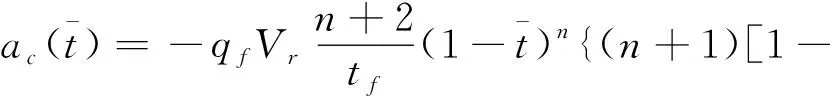
(33)

对式(33)两端求导，并令其为零，可得过载指令在极值点对应的时间为

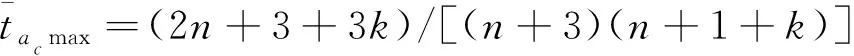
(34)

将式(34)代入式(33)，可得末制导过程中的极大需用过载为

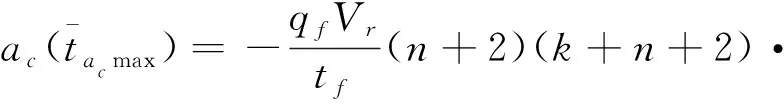
(35)

根据式(33)，末制导初始时刻和终端时刻的过载指令为

a

(0)=-

q

V

(

n

+2)(2

k

+

n

+1)

/t

(36)

a

(

t

)=0 (

n

>0)

(37)

由式(35)～式(37)可知，末制导过程中最大过载指令出现在末制导初始时刻或制导过程中。

末制导过程中的最大需用过载由

k

，

V

,

q

，

t

和

n

共同确定。当

k

，

V

,

q

,

t

确定时，可通过设计合理的制导阶次

n

来控制末制导过程中的最大过载指令。

2.2 导引头视角解析表达式

当终端落角较大时，容易引起目标跳出视场进而造成目标丢失，因此末制导过程中导引头视角应小于导引头视场角约束。

定义飞行器弹轴与弹目连线之间的夹角为导引头视角

φ

。为简化分析，假设制导过程攻角为一小量，则

φ

可近似表达为

φ

=

θ

-

q

(38)

飞行器与目标之间的相对运动关系为

(39)

联合式(38)和式(39)，导引头视角的变化率可表示为

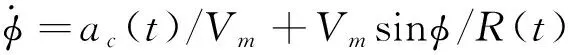
(40)

可见，在任意时刻当过载指令

a

(

t

)、弹目距

R

(

t

)已知时，可求得当前时刻的导引头视角。

R

(

t

)可表示为

R

(

t

)=

V

(

t

-

t

)

(41)

根据小角度假设，sin

φ

≐

φ

，将式(41)和式(29)代入式(40)，并考虑末制导初始时刻

φ

(0)=

ε

，则有

φ

(

t

)=

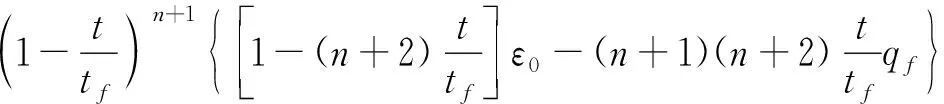
(42)

式(42)即为末制导过程中导引头视角的解析表达式。当已知

ε

,

q

,

n

和

t

，即可求得任意时刻的导引头视角大小。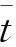

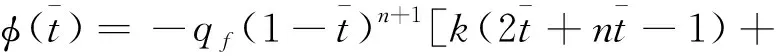
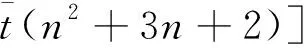
(43)

对式(43)两端求导，有

(44)

其中

(45)

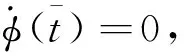
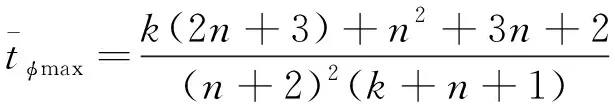
(46)

k

>

E

,

E

=-(

n

+3

n

+2)

/

(2

n

+3)

(47)

当

k

满足式(47)，将式(46)代入式(43)，可求得最大导引头视角为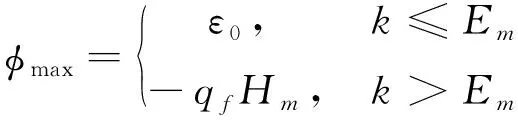

(48)

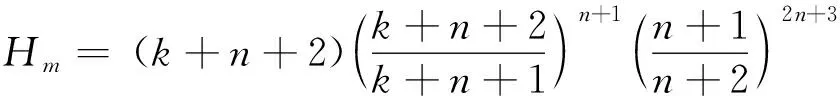
(49)

由式(48)可知，最大导引头视角由

k

,

q

,

n

共同确定。

H

在不同

n

时随

k

的变化趋势如图2所示。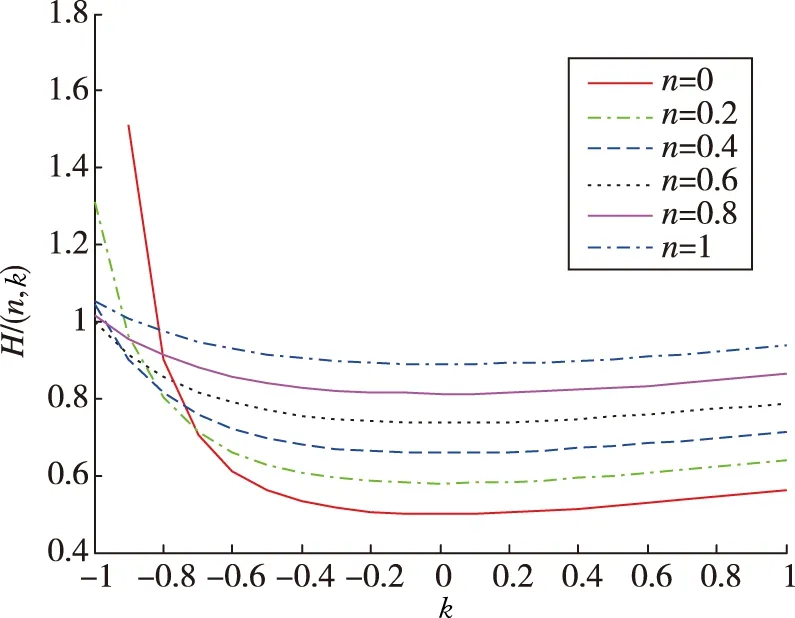

图2 H在不同制导阶次n时随 k变化曲线Fig.2 The relationship between H and k under different n

由图2可见，当

k

固定时，

n

越大，

H

越大；当

n

固定时，

k

绝对值越大，

H

越大，并且当

k

=0，

H

最小，即末制导初始速度方向指向弹目连线时，此时制导过程中的导引头最大视角为最小值。当

k

=

n

=0时，

H

=0

.

5，此时(

φ

)=-0

.

5

q

。

综上所述，可得出以下结论：

1)采用多约束最优末制导时，无论

k

,

q

,

n

如何取值，要保证末制导过程中目标始终处于视场内，导引头固有视场应大于落角的一半；2)在固有视场满足上述条件时，通过设计

n

来保证末制导过程中的最大视角满足导引头视场约束。

2.3 制导参数设计策略

满足飞行过载和导引头视角约束的制导参数设计原则为：分别以最大飞行过载和导引头最大视角作为设计约束来获取最优末制导律，同时在制导阶次可设计范围内选取较大值来保证终端过载指令归零。

满足飞行过载和导引头视角约束的制导参数设计流程如图3所示。

图3 满足飞行过载和导引头视角约束的制导参数设计流程Fig.3 Guidance parameter design process meeting flight overload and seeker angle constraints

2.3.1 满足飞行过载约束的制导参数设计

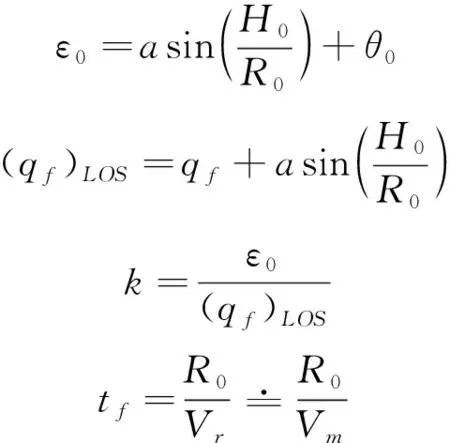
(50)

2)根据多约束最优末制导律最大过载

a

max解析表达式，令

n

取不同值时，求得当前初始条件下最大过载指令的最小值(

a

max)；

(51)

为保证终端过载指令归零，

n

需满足

n

>0。综上，考虑飞行过载约束的制导阶次

n

的取值范围为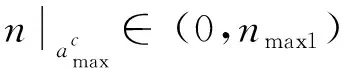

(52)

2.3.2 满足导引头视角约束的制导参数设计

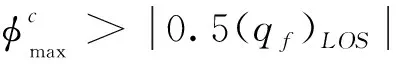
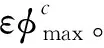
(53)

为保证终端过载指令归零，

n

需满足

n

>0。综上，满足导引头视角约束的制导阶次取值范围为

(54)

2.3.3 同时满足飞行过载及导引头视角约束的制导阶次

n

∈(0,

n

)∩(0,

n

)

(55)

3 仿真验证

在建立满足飞行过载、导引头视角等过程约束和满足落点位置、落角等终端约束的最优末制导律时，采用了小角度假设。下面通过仿真计算验证所得方法在非线性大角度条件下对机动目标的制导性能。

图4～图8给出了制导阶次

n

取0.8时，飞行轨迹、飞行过载、导引头视角、视线角和弹目距随目标不同初始速度倾角ThetaT的变化曲线。其中,图4中紫色虚线为目标在不同初始速度倾角时的飞行轨迹。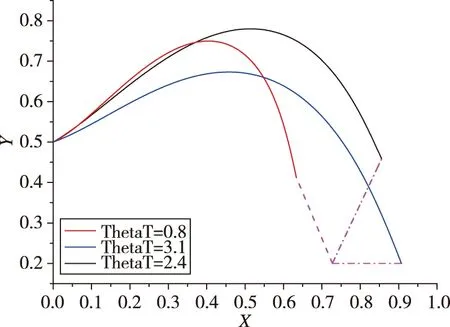

图4 飞行轨迹曲线Fig.4 Flight trajectory curve with different target initial velocity obliquity

图5 飞行过载变化曲线Fig.5 Flight overload curve with different target initial velocity obliquity

图6 导引头视角变化曲线Fig.6 Seeker angle of view curve with different target initial velocity obliquity

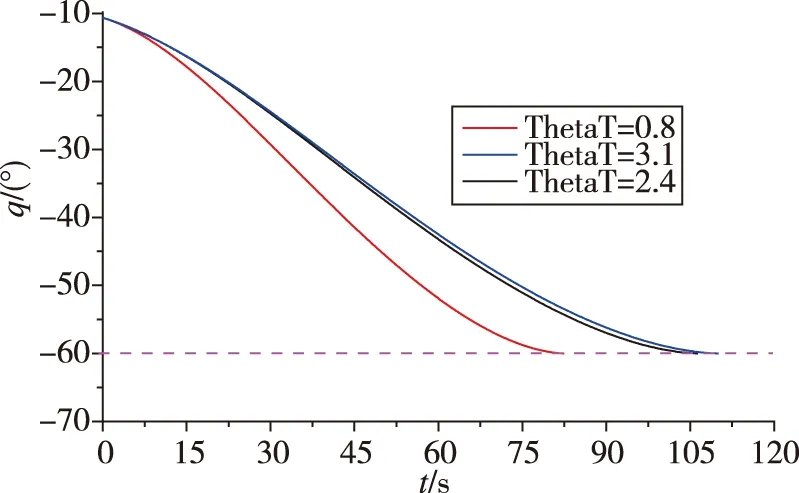
图7 视线角变化曲线Fig.7 Line of sight angle curve with ddifferent target initial velocity obliquity

图8 弹目距离变化曲线Fig.8 Distance between flight vehicle and target with different target initial velocity obliquity

通过仿真结果可见，多约束最优末制导律在非线性大角度条件下对机动目标具有较好的制导性能，能够满足终端位置和落角等终端约束以及飞行过载和导引头视角等过程约束。制导参数设计策略可解算出最优制导阶次取值范围，在取值范围内选取较大值，得到的最优制导律能保证飞行过程约束，并且可以使终端过载为一小值。

4 结论

针对复杂环境多约束条件下的飞行器末制导问题，本文设计了便于应用的满足落点位置和落角等终端约束以及满足飞行过载和导引头视角等过程约束的多约束最优末制导律，通过制导参数策略设计、制导律特性分析及仿真计算，验证了方法的有效性和正确性。