低速巡飞弹非匹配干扰观测控制器设计

卢庆立，孙瑞胜，王 娜,2，文 永

(1.南京理工大学能源与动力工程学院，南京 210094；2.北京航天无人机系统工程研究所，北京 100094)

0 引言

低速巡飞弹是一种小尺寸、低成本，集侦察、定位、评估、攻击等多种作战任务为一体的新概念武器。相比于无人机，巡飞弹可像常规弹药一样，采用多种武器平台发射，快速接近作战区域，有效规避敌军火力拦截，隐身突防能力强。相比于制导弹药，它又多出一个巡飞弹道，滞空时间长，作战范围大，可侦察并攻击隐藏的时间敏感目标。

巡飞弹多采用大展弦比、高升阻比的面对称气动外形和倾斜转弯(Bank-to-turn, BTT)控制方式。然而，巡飞弹BTT机动过程中，由于滚转通道的高速运动，使得俯仰和偏航两个通道存在严重的动力学耦合。此外，巡飞弹尺寸小、飞行速度低，周围气体流动特性复杂，受到风等外界干扰影响很大，动力学模型存在较大的非线性和不确定性。

针对上述问题，后德龙等和童春霞等分析通道之间的相互影响，对每个通道进行独立解耦设计。Mattei等则采用反演法直接对一个多输入、多输出系统进行控制律设计，解决了通道之间的耦合问题。魏铃等利用滑模变结构克服参数摄动和外界干扰造成的不确定性，却忽略了通道之间的耦合作用。上述研究都只考虑了不确定性或者耦合一个方面，而王昭磊等针对这两个问题采用反演控制和自适应控制相结合的控制方法，取得了一定的效果，但加入复合干扰后，系统出现抖振现象。方群等则采用神经网络估计不确定项，同时利用反演法克服了通道之间的耦合，获得很好的效果。对于不确定项的估计，杜立夫等和马建伟等则采用扩张状态观测器的方法，将不确定项扩张成一个状态，实时估计补偿。

干扰观测器同样可对非线性系统的不确定项进行估计，并且由于物理意义明确，工程实现简单，且能够在不改变原控制系统结构的基础上提高控制精度，应用广泛。李雯雯等和陈阳等在利用一种非线性干扰观测器对系统干扰进行估计的前提下设计控制律，获得良好的控制效果，但是均假定外界干扰变化缓慢，近似于常值，实际上这种约束在工程实践中很难满足。Chen等则不再要求干扰接近常值，指出对于变化率有界的干扰，此种观测器的估计误差有界，以此设计的控制系统状态稳定，但是存在误差。卢昊等针对包含多源干扰的非线性导弹系统，通过此类非线性干扰观测器估计复合干扰，并将估计结果代入反演法的控制律中，提高系统的抗干扰性能;但是并没有考虑干扰观测器的估计误差对控制性能的影响。于靖等则采用改进的边界层自适应滑模控制抵消干扰观测器估计误差的影响，获得了非常好的控制效果。

本文提出了一种基于干扰观测器的自适应反演控制方法。在反演控制的基础上，利用干扰观测器估计动力学模型中的不确定项，抵消不确定项对控制系统的影响。此外，采用自适应方法进一步克服因为干扰观测器存在估计误差带来的系统不确定性，提高控制系统的鲁棒性。与其他研究相比不同之处在于：1)以具有不确定性、强耦合特性的低速巡飞弹BTT控制系统模型作为研究对象；2)将一种用来估计常值干扰的非线性干扰观测器应用在变化率有界的时变干扰的估计中，推导出估计误差的有界性，推广了这类非线性干扰观测器的应用范围；3)反演控制的虚拟指令中加入抵消非匹配干扰的部分，提高了控制系统的抗干扰能力；4)为抵消干扰观测器存在的有界干扰误差设计了自适应调节律，保证了系统在李雅普诺夫意义下的稳定性要求。该方法直接对多输入多输出控制系统进行反演控制律设计，解决了控制系统的各状态量耦合问题，抵消了系统干扰和不确定性带来的影响，系统不仅具有较强的鲁棒性能，同时也具备较好的瞬态响应性能。研究成果可为低速巡飞弹控制系统设计研究提供参考依据。

1 动力学建模

考虑以下3个因素：1)低速巡飞弹，受周围复杂的气体流动特性影响，气动参数存在不确定性，导致动力学系数摄动较大；2)巡飞弹体积小、质量小，飞行过程中受风等外界干扰的影响较大；3)舵机作为控制系统的执行机构，并非理想环节，对控制量指令的响应有一定的偏差。为此，参考王娜等和王广山等研究成果，可将具有不确定项的巡飞弹动力学模型描述为

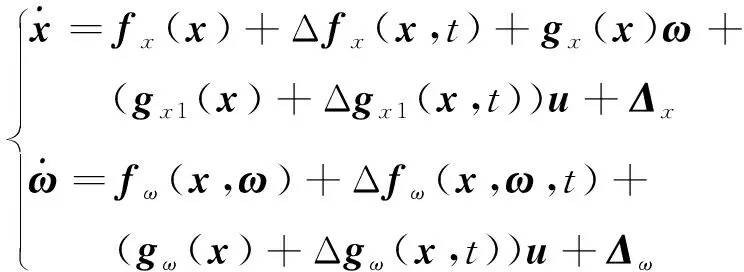
(1)

其中

(2)

(3)

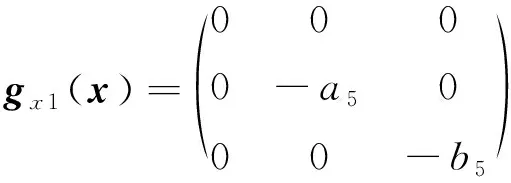
(4)

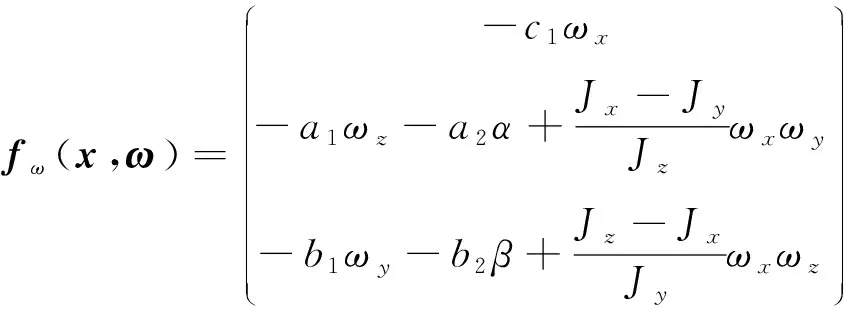
(5)

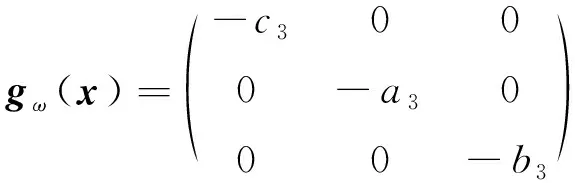
(6)

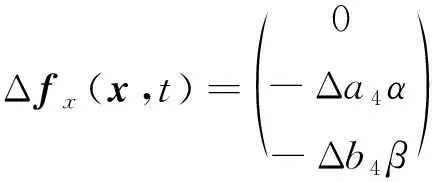
(7)

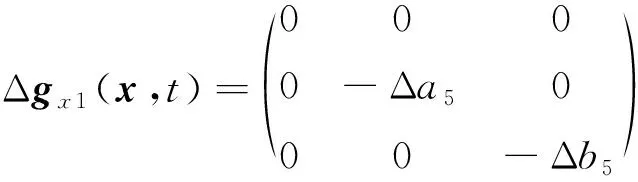
(8)

(9)

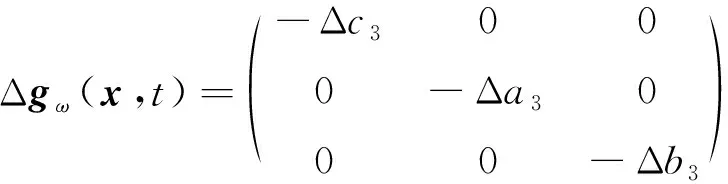
(10)

(11)

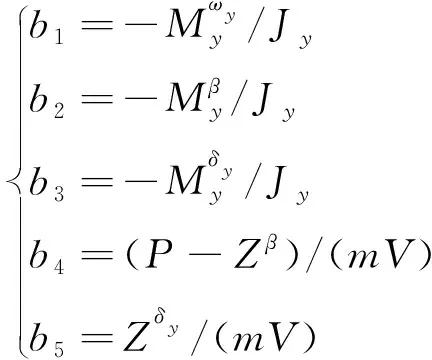
(12)

(13)

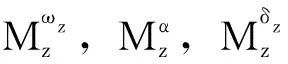
(14)

式中，=(,,

t

)+(,

t

)+,=(,

t

)+(1()+Δ1(,

t

))+。

2 控制器设计

本节对非线性控制系统设计基于干扰观测器的自适应反演控制器，使得控制系统在满足稳定性和鲁棒性的前提下，能够快速准确跟踪指令信号，具有良好的瞬态响应性能。

2.1 非线性干扰观测器设计

由上述分析可知，巡飞弹系统存在很大的由参数摄动和外界干扰组合而成的复合干扰，并且这种干扰是时变的。如果不对系统的复合干扰进行实时估计补偿，单纯在反演控制中加入自适应控制律，会导致系统发生抖振，跟踪精度达不到工程实际要求。针对巡飞弹BTT控制系统这种外界有时变干扰、参数有很大不确定性的非线性耦合系统，复合干扰的估计是必要的。本文设计的非线性干扰观测器允许复合干扰存在有界的变化率，只需根据系统标称模型，实时获得系统的可量测状态量就可以对干扰进行估计，估计误差在短时间内收敛，具有实现简单、运算快速的优点。

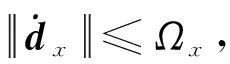
(15)

(++)

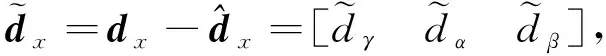
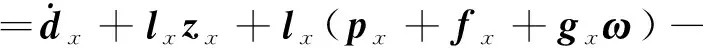
(16)

将上式写成标量的形式，即

(17)

(18)

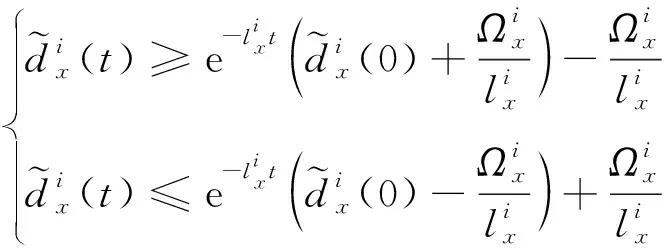
(19)

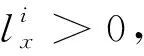
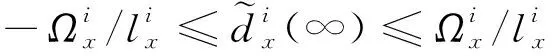
(20)

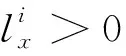
2.2 自适应反演控制律设计

基于反演控制的思想，将设计的干扰观测器估计的匹配干扰和非匹配干扰代入到反演控制的每一步中，并为干扰观测器存在的估计误差设计相应的自适应控制律，抵消其对控制系统的影响，以提高巡飞弹控制系统的鲁棒性。

对于加入干扰观测器的巡飞弹控制系统可进一步表示为

(21)

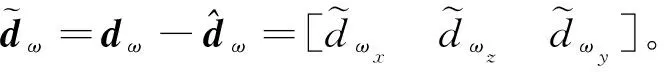
利用反演控制思想，对这样一个严格反馈两级非线性系统设计控制律来抵消非匹配项干扰和匹配项干扰，具体包括以下两个步骤：

第1步：非匹配项干扰的抵消

针对非匹配项干扰，在控制量中加入上节介绍的干扰观测器估计值和对估计误差设计的自适应律予以抵消。

考虑角跟踪误差微分方程

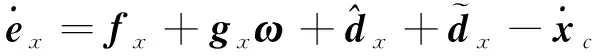
(22)

式中，=[

γ

α

β

]为角参考指令，=-为角跟踪误差。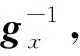

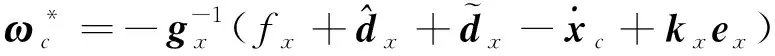
(23)

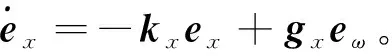
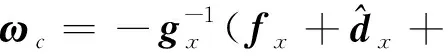
(24)

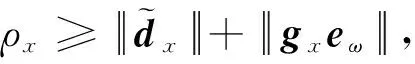
(25)

将式(24)和(25)代入式(22)可得

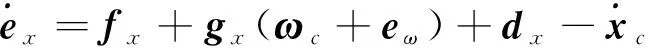
(26)

考虑李雅普诺夫函数

V

(27)

对

V

求导可得

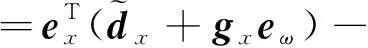
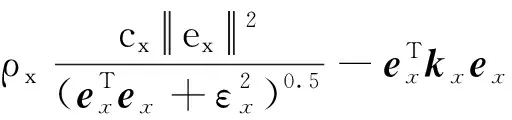
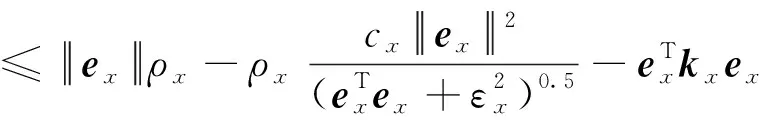
(28)

第2步：匹配项干扰的抵消

针对匹配项干扰，利用同非匹配项干扰一样的方法予以抵消。

考虑角速度跟踪误差微分方程

(29)

(30)

=

(31)

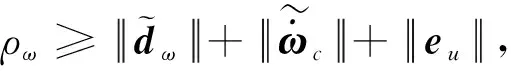
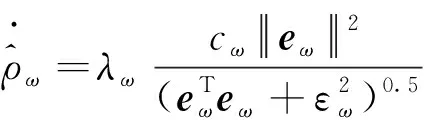
(32)

式中，

λ

,

c

,

ε

为待设计的正的参数。

将式(31)和(32)代入式(29)可得

(33)

考虑李雅普诺夫函数

V

(34)

对

V

求导可得

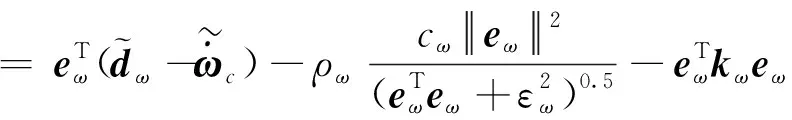
(35)

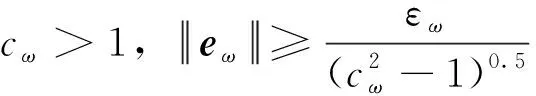
综上，对于式(1)这个包含不确定项的非线性系统，将动力学系数摄动和外界干扰看作复合干扰，采用式(15)所示的非线性干扰观测器估计等效干扰，同时为其存在的估计误差设计相应自适应控制律。将干扰观测器的估计结果和为抵消干扰观测器估计误差而设计的自适应控制律一起代入如式(24)和(31)所示的反演控制律中，自适应调节律分别选择式(25)和(32)的形式，以此来抵消系统不确定项的影响，保证闭环系统的渐进稳定。

3 数值仿真

3.1 仿真方案

为验证本文所研究的基于干扰观测器的自适应反演控制方法的正确性与有效性，将上述控制律用于低速巡飞弹倾斜转弯控制的数值仿真，并将仿真结果与没有干扰观测器的自适应反演控制仿真结果进行对比研究。

仿真条件如下：巡飞弹飞行速度为40 m/s，飞行高度为300 m；转动惯量

J

=0

.

64 kg·m，

J

=0

.

79 kg·m，

J

=0

.

64 kg·m；动力学系数均向上摄动20%，外界环境干扰为Δ=[0

.

7sinπ

t

动力学系数如表1所示。

表1 动力学系数仿真参数表

舵机作为控制系统的执行机构，其对控制系统的影响至关重要，故而在仿真中加入舵机模型

(36)

式中,

c

(

t

)是舵机系统输出量，

r

(

t

)是舵机系统输入量。

3.2 阶跃信号输入仿真结果

阶跃信号是控制系统最严格的输入条件，图1～5给出了输入为阶跃信号的仿真结果对比曲线，分析仿真结果可以得到以下几点结论：

1)从图1可以看出，非线性干扰观测器估计误差在短时间内收敛到一个很小的范围内，但是在收敛之前估计误差相对较大，估计误差的存在对控制系统瞬态响应性能和鲁棒性都有影响；

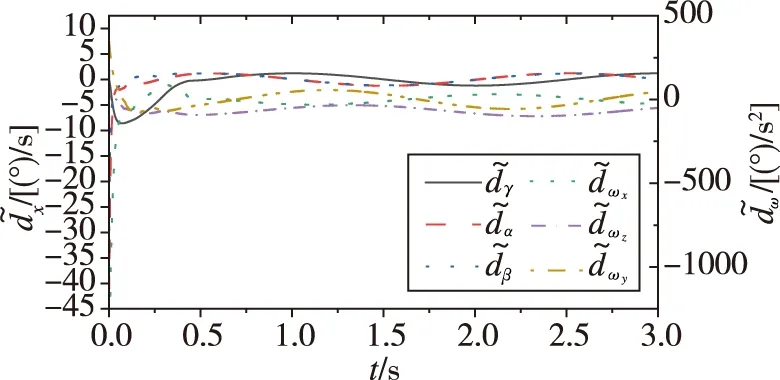
图1 干扰估计误差Fig.1 Angle disturbance estimation error

2)从图2～3可以看出,有干扰观测器的自适应反演控制系统具有跟踪精度高，系统响应抖振极小，调节时间短等优点，而没有干扰观测器的自适应反演控制系统响应抖振剧烈，始终不能稳定在期望终值，跟踪精度达不到工程实践的要求；

图2 滚转角跟踪对比Fig.2 Roll angle tracking contrast

3)从图4可以看出，两种控制方法侧滑角均在3°以内，这说明利用多输入多输出的反演法能够解决巡飞弹倾斜转弯带来的耦合问题，并且有干扰观测器的自适应反演控制系统能够快速将侧滑角控制在0°，为其他两个通道响应制导指令，实现巡飞弹BTT控制提供了有利条件；

图3 攻角跟踪对比Fig.3 Attack angle tracking contrast

图4 侧滑角跟踪对比Fig.4 Sideslip angle tracking contrast

4)从图5可以看出，两种控制方法舵偏角的变化范围及变化速率均在允许范围内，无剧烈振颤，不会突破舵机执行的物理限制，便于舵机执行。

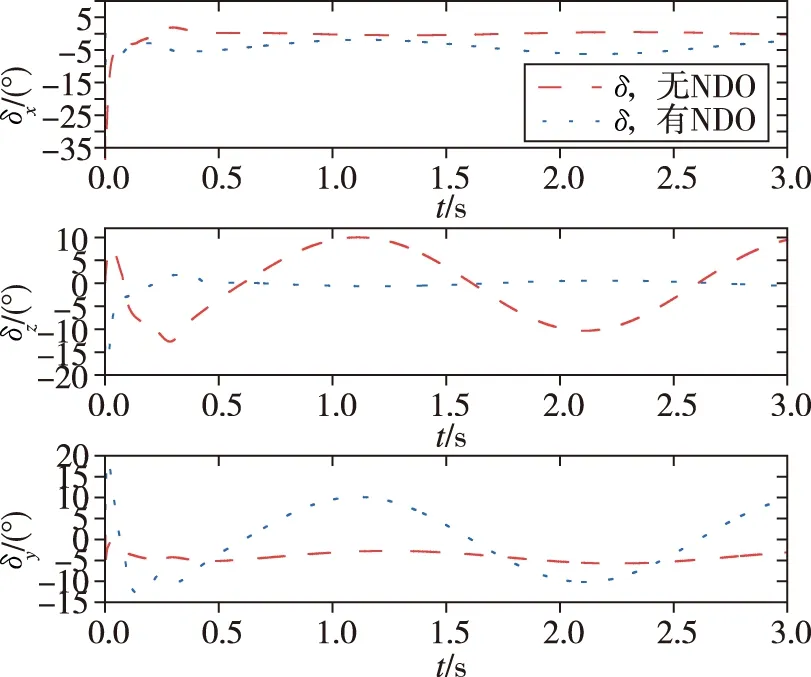
图5 舵偏角对比Fig.5 Rudder angle contrast

3.3 正弦信号输入仿真结果

正弦输入信号可以考察控制系统对于变化的输入指令的响应能力，图6～10给出了输入为正弦信号的仿真结果对比曲线，分析仿真结果可以得到以下几点结论：

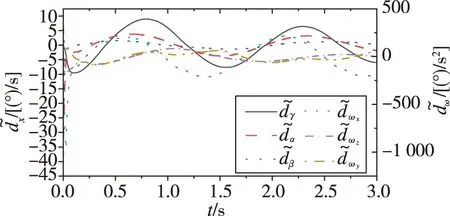
图6 角度干扰估计误差Fig.6 Angle disturbance estimation error

1)从图7～8可以看出,有干扰观测器的自适应反演控制系统比没有干扰观测器的自适应反演控制系统相位滞后要小;同时可以看出,没有干扰观测器的自适应反演控制系统对信号幅值的放大作用明显，跟踪精度较差；

图7 滚转角跟踪对比Fig.7 Roll angle tracking contrast

2)从图9可以看出，虽然滚转角和攻角随指令周期性变化，但是两种控制方法的侧滑角仍然在3°以内，这更能说明利用反演法能够解决俯仰和滚转角速度对侧滑角和侧滑角速度的耦合问题。只是有干扰观测器的自适应反演控制系统能够快速准确地将侧滑角控制在0°，表现出更好的控制性能；

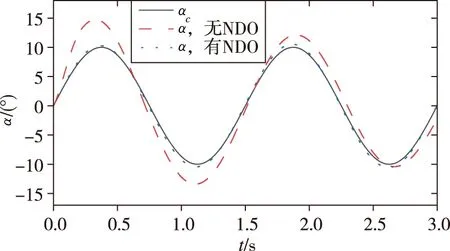
图8 攻角跟踪对比Fig.8 Attack angle tracking contrast

图9 侧滑角跟踪对比Fig.9 Sideslip angle tracking contrast

3)从图10可以看出，两种控制方法舵偏角的变化范围及变化速率均在允许范围内，无剧烈振颤，不会突破舵机执行的物理限制，便于舵机执行。

图10 舵偏角对比Fig.10 Rudder angle contrast

4 结论

本文针对低速巡飞弹倾斜转弯时控制系统存在耦合与不确定项的问题，研究了一类基于干扰观测器的自适应反演控制方法。非线性干扰观测器不需对系统的诸多干扰进行准确建模，能够快速准确地估计出匹配干扰和非匹配干扰，为反演控制提供了前提条件，同时能够避免传统鲁棒控制由于无法获知干扰全部信息而工作在非最优状态下导致的稳态误差过大现象。与系统实际干扰相比，干扰观测器的估计误差是个小量，而利用自适应调节律抵消这部分的影响，不会出现如前所述的稳态误差较大现象。仿真结果表明，基于干扰观测器的自适应反演控制方法相比于传统的自适应控制，能够更加快速准确跟踪角参考指令，控制系统具有强鲁棒性。