一种卷积神经网络的模型压缩算法

包志强，程 萍，黄琼丹，吕少卿

(西安邮电大学通信与信息工程学院，陕西 西安 710121)

0 引 言

近年来，卷积神经网络[1-3](Convolutional Neural Network, CNN)在目标检测[4-5]、图像分类[6-7]等领域取得诸多重大的研究成果。这很大程度上要归功于对网络架构的创新，虽然各种网络结构存在差异，但这些任务使用的是相似的优化技术[8]。这些技术将每个权重视为单独的个体并独立更新，在CNN的训练方面取得了有限的进展。而事实上，网络权重之间有很大的联系，卷积核在提取特征时总是存在着不必要的重叠[9-12]。

目前深度网络模型压缩与加速方法研究主要有以下几个方向：

1)设计更精细的网络结构，直接提出新的卷积计算方式，从而减少参数，达到压缩模型的效果，如SqueezeNet[13-14],以及修改网络结构ERFNet[15]。轻量级网络ShuffleNet[16]，这种新的CNN架构利用逐点群卷积和通道混洗操作使计算量大大降低。重新构建新型网络虽然可以降低模型大小，但对于网络结构的选择，模型不同设计思路也不同，且其自身的模型压缩也是一个难题。

2)核的稀疏化，是在训练过程中对权重更新以正则项进行诱导，使卷积核更加稀疏，稀疏化后，裁剪更加容易。Jin等人[17]通过训练一个稀疏度较高的网络降低网络模型的计算量。Lebedev等人[18]对参数矩阵进行稀疏化正则约束，在损失函数中添加正则项，使训练中的矩阵参数值逐渐趋于零。Wen等人[19]提出结构化稀疏学习方法，通过对卷积核、卷积核形状和网络层数等学习一个稀疏结构来降低计算能耗。稀疏化方法不需要预训练网络，实现过程简单，但模型性能对稀疏正则化系数较为敏感，故设置最优的正则化系数比较困难。

3)模型裁剪,是目前模型压缩中使用最多的方法，对于已训练好的网络模型寻找一种有效的评价手段，剔除不重要的卷积核减少冗余。2015年，Han等人[20]将网络裁剪的思想应用到卷积神经网络上，在不损失网络精度的前提下使网络模型可移植到嵌入式设备上。Sun等人[21]提出一种基于神经元激活相关性的重要性判别方法，由此来降低模型的复杂度，且在人脸识别任务上的效果很好。Yang等人[22]采用一种基于能量消耗的裁剪方式，对每层消耗的能量排序，优先裁剪能耗大的层。

模型剪枝技术能够较方便地对预训练模型选择合适的评价标准，以寻找网络中的冗余参数，且可以省去重新训练的成本。因此为了解决卷积层权重冗余问题，本文采用一种针对卷积层的模型剪枝压缩方法，裁剪冗余参数，压缩网络，并且不会影响网络的性能；同时，提出参数正交正则，促进卷积核之间的正交化，提高训练的稳定性。

1 卷积核相关性分析

1.1 卷积核性能评估

本文构造一个含有3层卷积、2层全连接的CNN，其中卷积核参数设置见表1。为了评估每个卷积核对模型性能的重要性，分别计算第1、第3层卷积层删除卷积核后测试集精度的下降量。绘制下降精度的分布结果如图1与图2所示。从图中可观察到，第3层大部分卷积核的重要性不到1%，而第1层分布范围较广，有些卷积核的重要性达到4.5%，近一半的卷积核的重要性约为1%。这表明即使是简单的网络也可以剪枝卷积核而不显著影响性能。

图1 第1层卷积核性能评估

图2 第3层卷积核性能评估

表1 卷积核参数

1.2 卷积核相关性

实验使用皮尔逊相关系数判断同一层不同卷积核之间的相关性，皮尔逊相关系数可以度量2个量之间的线性相关程度。某一层的卷积核K∈Rk×k×Cin×Cout,k为卷积核大小，Cin、Cout分别为卷积核输入与输出的通道数，则该层卷积核数为Cin×Cout。在计算相关系数时，将每个二维卷积核拉伸成一维，则每个卷积核的参数量为k2。其计算方法如式(1)，ρKi,Kj的值介于-1与1之间。

(1)

(2)

(3)

(4)

2 训练策略

2.1 训练算法

网络进行一定数量的标准训练后，计算同一层不同卷积核参数间的皮尔逊相关系数，设置一定的相关系数阈值，删除相关度较高的冗余参数，同时采用局部-全局微调策略，再循环以上操作继续训练，直到网络收敛到理想位置。训练策略的算法流程如图3所示。

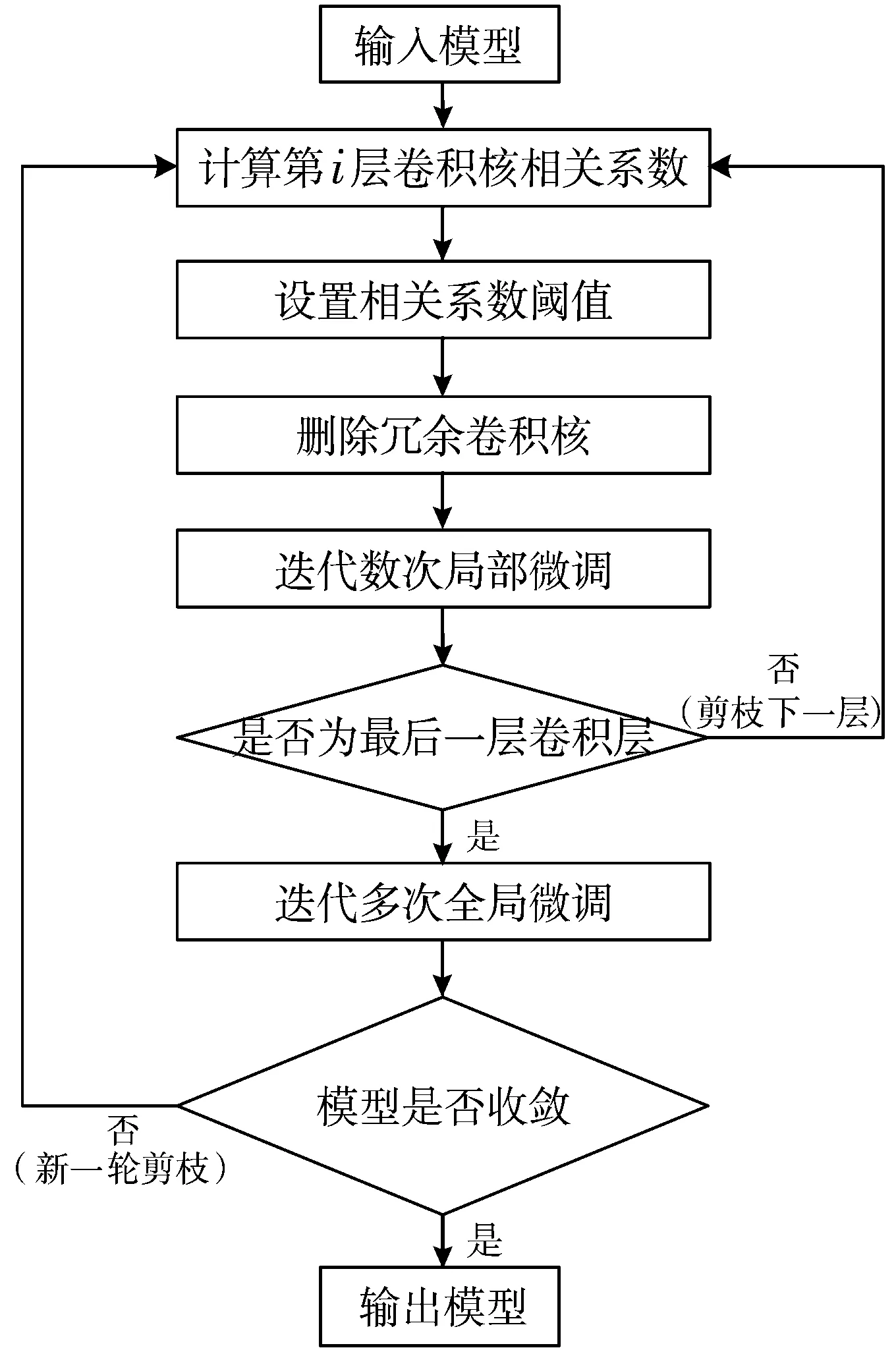
图3 算法流程图

具体的剪枝操作过程，以第1层卷积层为例，卷积核个数为32，即K1,K2,…,K32。在该层第1轮剪枝中，首先分别计算K1与K2,…,K32的皮尔逊相关系数，若该值大于设定阈值，则剪枝K2,…,K32中与K1相关度高的卷积核，且剪枝的卷积核不参与该层接下来的相关系数计算过程。同样地，对上述剪枝操作的结果，再次分别计算K2与剪枝后的卷积核K3,…,K32的皮尔逊相关系数，根据阈值剪枝与K2相关度较高的卷积核，以此类推，直到完成该层第1轮剪枝，微调后，再对余下的卷积层进行相同的剪枝操作。

2.2 局部-全局微调

为了平衡训练速度与测试精度，本文采用一种局部-全局微调的训练策略。当每一层卷积核剪枝后，网络通过少数迭代局部微调，以稍微恢复其性能。只有在最后一层被剪枝后，才通过较多的迭代全局微调，以恢复整体的性能。使用这种微调策略，可以大大减少整个网络的训练时间，同时，也可以避免微调后的网络在早期学习阶段进入局部最优。

2.3 参数正交正则

训练过程中，为了诱导同层之间的卷积核保持正交，使卷积核之间的重叠信息保持最少，在模型原有的交叉熵损失函数基础上，提出参数正交正则，替代L2正则化，增强参数的非相关性，约束过拟合，对权重更新进行诱导，促进核的稀疏化，更易于参数的裁剪。

在神经网络中，网络的输入与输出的关系为y=WTx，当W为实正交矩阵时，WWT=I，则存在‖y‖=‖x‖，这种线性变换称为范数不变性，推导如式(5)，该式成立的条件为当且仅当WWT=I。

(5)

则可推导出每层卷积核的参数正交正则如式(6)：

(6)

其中，λ为正则化系数，Wi为某层卷积核的二维参数矩阵，Wi每一行表示每个卷积核的权重展开，I为单位矩阵，‖·‖F为矩阵的F范数。且当WiWiT=I时，Wi为正交矩阵。

此时损失函数为交叉熵损失cross_entropy与参数正交正则损失之和，如式(7)。对于式中正则化系数λ值的确定，首先给定一个初始值1.0，根据验证集的准确率，调整合适的λ数量级，经过多次实验对比，λ的值最终确定为0.0001。

(7)

3 实验结果及分析

3.1 运行环境

实验运行的硬件环境为台式计算机，配有主频4.8 GHz的6核CPU、8 GB内存、RTX3070显卡。软件环境为Python 3.5，深度学习框架为TensorFlow。

3.2 参数量及FLOPs

参数量以参数个数为度量标准，卷积核K∈Rk×k×Cin×Cout,k为卷积核大小，Cin、Cout分别为卷积核输入与输出的通道数，在不考虑偏置的情况下，卷积层的总参数量为k×k×Cin×Cout。经过一定数量标准训练后，设置不同相关系数阈值可计算每个卷积层的冗余参数量。

卷积层的浮点操作计算量(Floating Point Operations, FLOPs)用来衡量卷积操作的复杂程度，即完成卷积操作需要执行乘法和加法的次数。假设卷积核大小为kH×kW，输出特征图为Hout×Wout，Cin、Cout分别为卷积核输入与输出的通道数。一张输出特征图的计算量为Cin×kH×kW次乘法操作及Cin×kH×kW-1次加法操作，输出通道数相当于输出Cout个特征图，在不考虑偏置的情况下，卷积层的FLOPs为(2×Cin×kH×kW-1)×Cout×Hout×Wout。

3.3 实验结果

实验采用基于Python的TensorFlow[23]开源框架实现卷积层压缩算法。构造一个有3层卷积、2层全连接的CNN，利用该算法剪枝网络模型，具体某一卷积层剪枝后的效果如图4所示，图中符号*表示卷积操作。

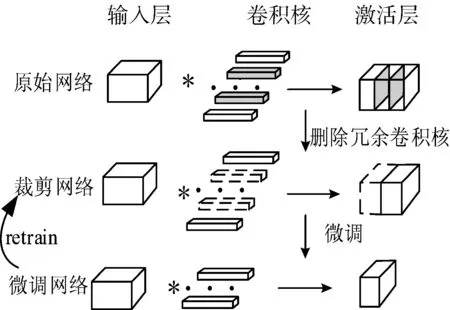
图4 某一卷积层剪枝网络图

实验中的批样本数batch_size为100，学习率为0.01。为防止学习率过大，使得模型在收敛过程中来回摆荡，故设置学习率衰减指数为0.99，使学习率随着训练轮数不断下降。表2中的实验结果以选取相关系数阈值0.7为例，列举了卷积层参数量及浮点操作计算量FLOPs的压缩率。在计算参数量及FLOPs时，偏置的量忽略不计。从表2中压缩率数值可知，随着网络深度的加深，卷积核之间的相关性越高，第3层卷积层参数压缩率为68.5%，FLOPs压缩率为47.6%，总体卷积层的压缩率为39.1%, FLOPs可以减少19.8%。表3为原始网络与每轮剪枝微调后网络精度对比结果，图5为网络压缩前后的损失值对比图，可以发现经过5轮裁剪后的网络精度略高于原始网络，且压缩后的网络可以使模型收敛到较小的误差。

图5 原始网络与压缩后的损失对比

表2 3层卷积层网络的参数量及FLOPs压缩率

表3 原始网络与压缩后的网络精度对比

为了验证该训练策略的通用性，实验选取有5个卷积层的AlexNet[24]网络训练MNIST数据集。表4分别列举了AlexNet使用参数稀疏策略后卷积层参数量及FLOPs的压缩情况。从表中数据可以看出，AlexNet卷积层的参数量压缩率为53.2%，FLOPs的压缩率为42.8%。AlexNet卷积层压缩量达到一半以上，表明该训练策略同样适用于复杂的网络。

表4 5层卷积层网络的参数量及FLOPs压缩率

从以上实验结果可以看出，训练良好的网络模型易于裁剪而不降低精度，表明卷积核在提取特征时存在着大量不必要重叠。该训练策略不仅减少了学习特征过程中的重叠，减少卷积层计算成本，而且使模型的泛化能力进一步提高。

4 结束语

本文观察到大部分卷积核对网络性能的贡献度较小，且同一层卷积核之间存在联系，提出一种针对卷积层的模型压缩训练策略，改善卷积神经网络参数计算量大的现状。根据皮尔逊相关系数剪枝参数，并采用局部-全局的微调方法调整网络性能，同时在损失函数中添加参数正交正则，增强卷积核之间的非相关性，使卷积层提取的特征重叠信息保持最少。实验结果显示，在MNIST数据集上，使用该训练策略分别对具有3层卷积层的网络及AlexNet网络进行训练，卷积核参数量及FLOPs在很大程度上得到了压缩。同时改进后的模型可以达到原网络同样高的精度，损失函数也可以收敛到理想的位置。

由于设备的限制，接下来的研究会进一步补充实验，将该压缩算法应用于更加复杂的网络来验证其性能。同时，寻求更加优化的评判卷积核重要性的方法。