基于深度学习的SuperDARN雷达极区电离层跨极盖电场模型构建

李可 刘二小

(杭州电子科技大学通信工程学院,浙江 杭州 310018)

提要 通过超级双子极光雷达网(SuperDARN)获得的跨极盖电势计算了极区电离层对流电场。利用2014年的极区电离层对流电场数据为基础,引入对流电场的历史数据,分别基于多元线性回归算法和后向传播神经网络算法构建电离层电场模型。利用独立的数据集,验证了两种模型的准确性和稳定性。结果表明,模型值与测量值的均方根误差在2.0～3.5 mV·m-1之间,平均绝对误差范围为1.5～3.0 mV·m-1,线性相关系数均大于0.6,最高可达0.9。引入前20 分钟的历史数据作为模型的输入,后向传播神经网络模型比多元线性回归模型具有更好的预测性能。

0 引言

极区电离层作为极区高空大气的重要组成部分,电离层对流电场的研究有助于我们理解和把握电离层电动力学过程。电场模型的构建是其中有效的方法之一。本文的跨极盖电场由跨极盖电势(Cross Polar Cap Potential,CPCP)推导而来,而跨极盖电势是表征电离层对流强度的参数,对于空间天气变化也有很强的指示作用,有关跨极盖电势的研究已经在磁层-电离层耦合领域持续了多年,并且在空间天气现报和预报中起着越来越重要的作用[1-2]。深度学习中的人工神经网络技术在过去几年中广泛应用于空间天气模型的构建和预报,并被证明是一种有效的工具[3]。

超级双子极光雷达网络(Super Dual Auroral Radar Network,SuperDARN)是一个国际性的雷达网络。目前,SuperDARN 由全球35 部雷达组成,基本覆盖电离层的高纬地区以及部分中纬度地区。SuperDARN 在研究磁层、电离层、热层以及中间层方面取得了很大的成功[4-5],已经逐渐成为监测高纬电离层对流的最强有力的工具[6]。Cousins和Shepherd[7]基于SuperDARN 雷达测量数据建立电离层等离子体对流对各种参数的依赖关系,如行星际磁场(Interplanetary Magnetic Field,IMF)、太阳风速度和地磁活动指数。Thomas 和Shepherd[8]推导出了由太阳风、行星际磁场和磁倾角组成的更完整的气候模型。Wilder 等[9]基于美国国防气象卫星(Defense Meteorological Satellite Program,DMSP)和SuperDARN 雷达研究了CPCP 模型随各类太阳风-行星际磁场参数的非线性关系。研究结果表明,通过线性拟合得到的CPCP 模型预测值与太阳风的阿尔芬马赫数存在显著的相关性,而与太阳风动压的相关性并不明显[9]。沈长寿等[10]发现受太阳风控制的磁层对流电场增强,在初期能直接从极光区穿透到中低纬电离层。Pozo 等[11]发现大规模对流电场是太阳风与地球外磁层之间的相互作用产生的,并且受到极光和极光下区域电离层与磁层之间的耦合的调制,为建立大规模对流电场自洽模型,推导出了改进的可变相位Stern-Volland 模型。Bristow 等[12]提出极区电离层对流不仅取决于太阳风和IMF 参数的瞬时值,还取决于它们的历史值,因此,本文通过引入对流电场的历史数据作为模型的输入来构建极区电离层电场模型。

Kan-Lee 重联电场是表征电离层对流的重要因子[13],最初是Kan 和Lee[14]提出的,其表达式为:

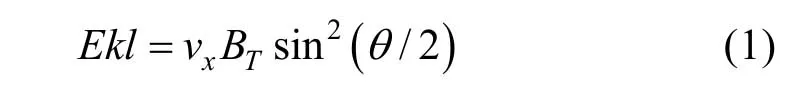
其中,Ekl为Kan-Lee 重联电场,xv为太阳风速,TB是横向IMF,θ是IMF 时钟角θ=arctan（BY/BZ）。

Shepherd 等[13]利用Kan-Lee 电场分析了电离层对流以及CPCP 的太阳风驱动因子,说明了太阳风和IMF 的值不足以描述CPCP 的瞬时值。Koustov 等[15]基于SuperDARN 雷达数据研究了跨极盖电势随行星际电场(Interplanetary Electric Field,IEF)、Kan-Lee 重联电场、北半球极盖指数(Polar Cap North,PCN)以及太阳风磁层耦合函数的关系。

前人的研究结果表明,电离层等离子对流受多种因素的影响,比如太阳风参数、行星际磁场IMF 分量、地磁指数等,因此构建电离层电势模型以及电场模型需综合考虑这些参数。同时由于电势不仅取决于太阳风/IMF 参数的瞬时值,而且还取决于它们的历史,故本文将电场的历史数据考虑进来,并分析了历史数据对电场模型的影响,从而寻找最佳时长的历史数据。

本文首先通过SuperDARN 雷达探测的极区电离层跨极盖电势数据,推导出了电离层跨极盖电场参量,然后分析了该电场与Kan-Lee 重联电场Ekl、极光电集流指数(Auroral Electrojet index,AE)、太阳风电场(Esw)、IMFBz分量等参数的相关性。在此基础上选取与极区电离层电场相关性较高的参数以及电场的历史数据,基于多元线性回归算法(Multivariate Linear Regression,MLR)和后向传播神经网络(Back Propagation Neural Network,BPNN)算法构建了电离层电场模型,并对模型进行了误差分析和评估。

1 数据处理

1.1 电离层电场数据

本文所使用的数据集是2014年SuperDARN雷达观测到的北极电离层电势和电场数据,时间分辨率为2 分钟。其中,1—6月份电离层电场数据作为训练数据集,7—12月份的数据作为测试数据集,用于对模型进行验证和评估。

在构建模型的过程中,由于数据中存在9.99、99.99、999.99 类似的无效数据,不利于训练模型,故将测量数据中的该类无效样本删除。同时,对雷达扇面内数据回波点达到一定数值的对流图像进行选择,数据回波点的选择同样对研究电离层对流电场有重要影响,Koustov 等[16]选择使用回波点数＞300 的数据,比Grocott 等[17]使用的回波点数＞200 的数据更为严格,所以在本文中同样挑选雷达测量回波矢量数＞300 的数据,重新整理后形成新的矩阵。图1 为SuperDARN 观测的全域对流图,图中红线表示跨极盖电势的最大电势点CPmax与最小电势点CPmin之间的距离d,利用跨极盖电势差CPCP=CPmax-CPmin和距离d计算可以得到跨极盖电场(Ef),表达式为Ef=CPCP/d。图2 表示了训练数据集与测试数据集观测电场值的直方图。由图可知,训练集和测试集的电场值绝大部分10～35 mV·m-1之间,而且二者的分布相似,因此本文可以忽略测试与训练之间数据的不平衡引入的误差[18]。

1.2 相关性分析

为了探究不同潜在的输入参数与对流电场之间的相关性,本文计算他们的线性相关系数(Linear Correlation Coefficient),公式如下:

其中,x为不同的输入参数,y为输出参数对流电场。

图1 SuperDARN 雷达在2014年2月6日13:32—13:34 UT 时刻观测的对流图 Fig.1.A typical SuperDARN convection map for 13:32—13:34 UT on 6 February 2014.

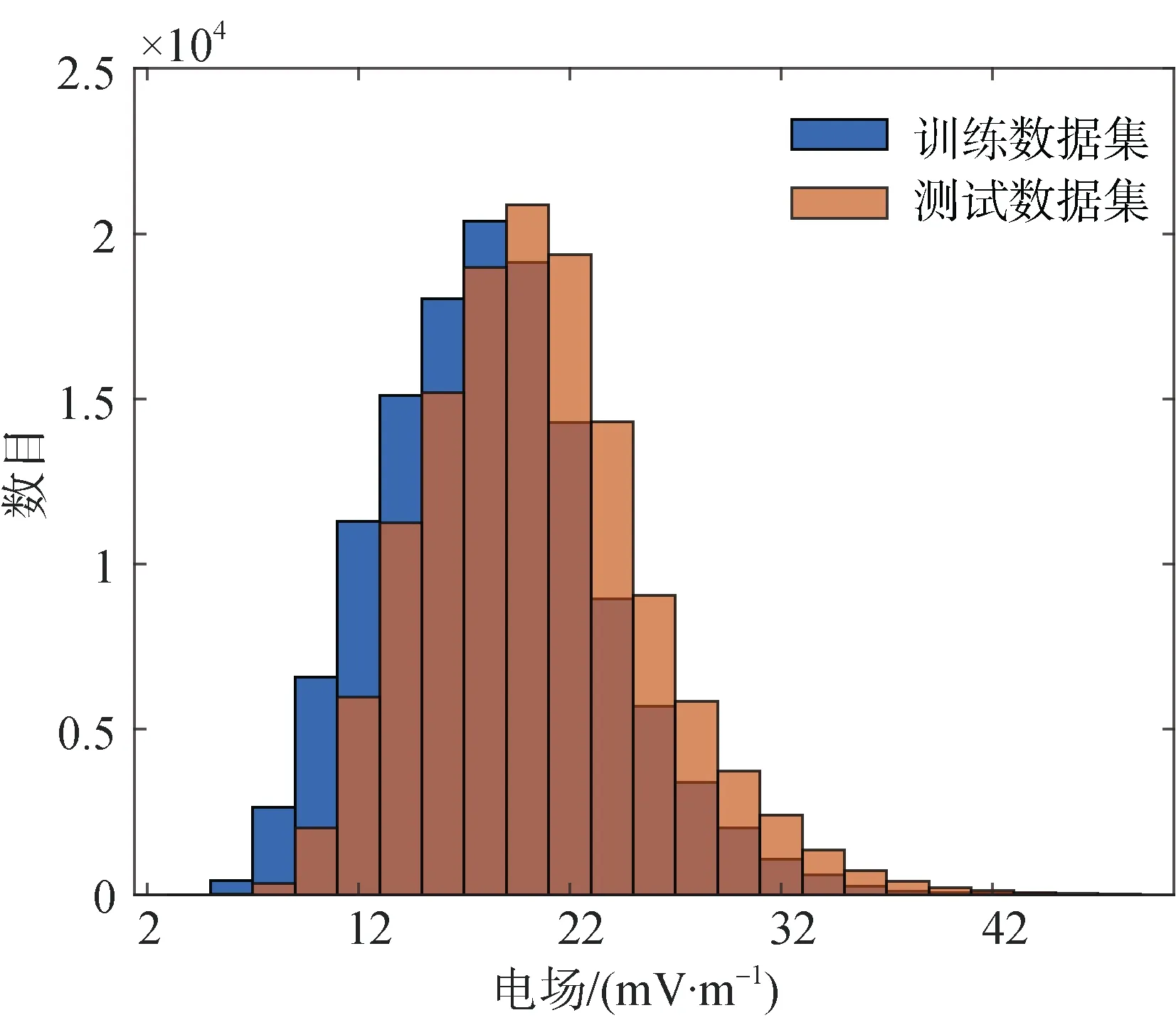
图2 训练数据集和测试数据集的对流电场值的直方图(蓝色部分为训练数据集,浅棕色部分为测试数据集,深棕色部分为两者分布的重叠部分)Fig.2.Histogram distribution of Convective electric field for train and test dataset.The blue part is the training data set,the light brown part is the test data set,and the dark brown part is the overlapping part of the two distribution.

本文引入了对流电场的历史数据,计算对 流电场不同时延时的自相关系数,结果如图 3所示。随着时延的增加,相关系数在不断减小,说明了不同时长的历史数据对对流电场瞬时值存在的影响也不同。对于日地空间参数的选择,本文从太阳风和IMF 参数中选取12 个参数来研究对流电场依赖关系,分别是行星际磁场 IMFBx、By、Bz分量、太阳风速Vsw、Vx、等离子体质子密度(Proton Density,PD)、流量压力(Flow pressure,Fp)、太阳风电场Esw、阿尔芬马赫数(Alfven Mach number,AM)、AE 指数、PCN 和Kan-Lee 重联电场,这些参数是影响电离层对流电场变化的潜在因素。图4 表示了对流电场与上述参数之间的相关系数的绝对值。可以看出IMFBz分量、太阳风电场Esw、AE 指数、Kan-Lee 重联电场Ekl与对流电场密切相关,相关系数在0.4 以上或很接近0.4。IMFBy分量和阿尔芬马赫数与对流电场呈中度相关,相关系数在0.1～0.3 之间。太阳风速Vsw、Vx、PD、Fp和PCN 与对流电场的相关系数均小于0.1,与对流电场的相关性较弱,甚至没有相关性。

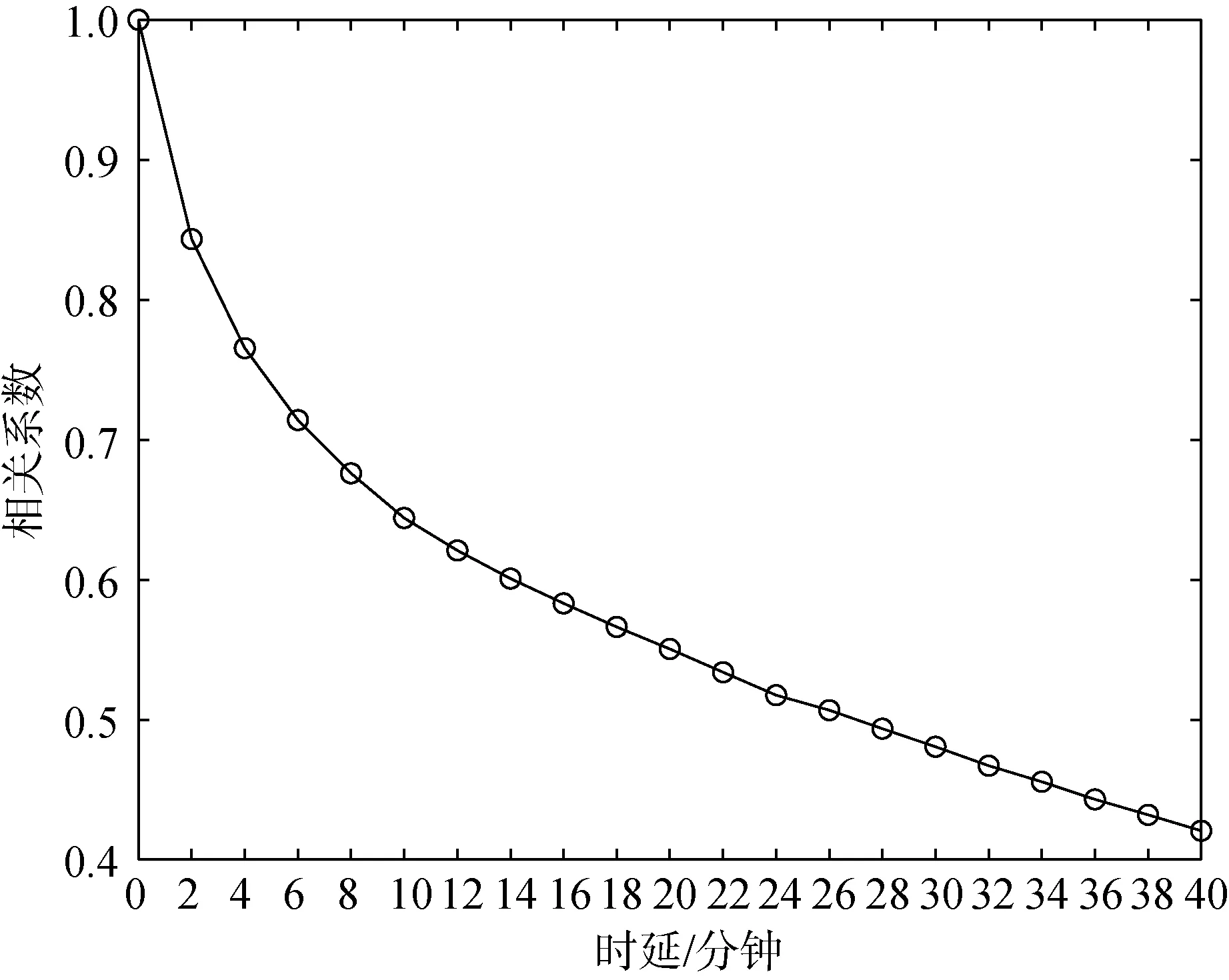
图3 不同时延的对流电场的自相关系数Fig.3.Autocorrelation coefficient of convective electric field with different time delays

图4 不同参数与对流电场的相关系数绝对值Fig.4.The absolute values of linear correlation coefficients between different parameters and convective electric field

基于相关系数,本文选取行星际磁场IMFBz分量、太阳风电场Esw、AE 指数、Kan-Lee 重联电场Ekl作为输入,同时将历史电场值Efh也作为输入构建电场模型。

2 算法

2.1 多元线性回归(MLR)模型

本文中,回归模型输入为行星际磁场IMFBz分量、太阳风电场Esw、AE 指数、Kan-Lee 重联电场Ekl以及对流电场的历史数据,分别记作为自变量,输出为电离层对流电场值记作y,为因变量,则多元线性回归模型为:

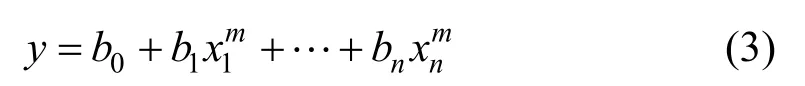
其中,m为样本个数,b0为常数项,b0,b1,…,bn为回归系数。

2.2 误差后向传播神经网络(BPNN)模型

1986年,Rumelhart 等[19]提出了后向传播网络模型(BP 神经网络模型),解决了单层感知器网络模型不能解决的问题。本文所使用的深度学习BP 算法基于Hinton 等人[20]在2006年开发的具有多隐藏层的深层神经网络,该网络具有很好的特征学习能力,通过无监督学习的方法训练每一个隐层,并将上一层训练的数据传递给下一层再训练,最后通过有监督学习的方法(BP 神经网络算法)调整训练好的整个网络[21]。同时,本文基于输出变量和输入变量之间的相关性分析,选取具有较高相关性的参量作为网络输入,极大地降低了深度神经网络的计算量。总体而言,基于深度学习的BP 神经网络算法改进了BP 神经网络算法存在的梯度越来越稀疏、从顶层越往下误差校正信号越小和容易陷入局部极小值的问题。

BP 神经网络算法是一种误差后向传播算法的多层前馈神经网络,是目前应用最广泛的人工神经网络。该算法具有结构简单、易于实现的优点,在故障诊断、模式识别等方面得到了广泛的应用[22]。从结构上讲,BP 神经网络具有输入层、隐含层和输出层; 从本质上讲,BP 神经网络算法就是以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值[23]。本文所使用的BPNN 模型架构如图5 所示。其中,每个圆形节点代表一个人工神经元,每个箭头代表从一个神经元的输出到另一个神经元的输入的连接。蓝色、黄色和紫色圆圈分别用于输入层、隐含层和输出层。输入层包含5 个用于输入特征参数的节点,分别为行星际磁场IMFBz分量、Esw、AE 指数、Kan-Lee 重联电场Ekl以及历史电场值Efh,而输出层只有一个节点为对流电场值。

图5 BP 神经网络结构Fig.5.Back Propagation Neural Network architecture

在建模过程中,输入样本向量为xm=测量值向量为zm=输入层到隐含层的连接权值为隐含层至输出层的连接权值为隐含层各单元的输出阈值为θj（1≤j≤K）,输出层各单元的输出阈值为γt（1≤t≤L）,g（x）和 f（x）分别为隐含层和输出层的传递函数。

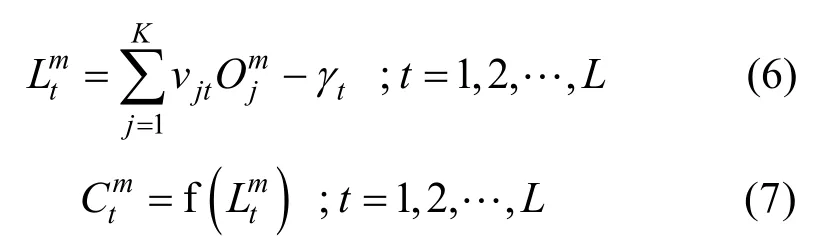
对于BP 神经网络算法,通常选择以Sigmoid型函数作为输出层和隐含层的传递函数,即:

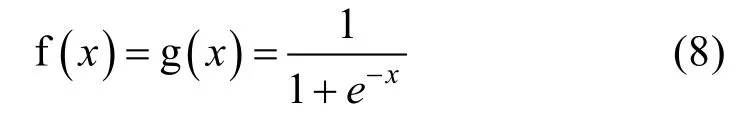
式中,-∞＜x＜∞。

3 模型评估

本文以2014年7—12月SuperDARN 雷达观测到的电离层电场数据为测试数据集,对模型进行评估。通过计算绝对误差(Absolute Deviation,AD)和相对误差(Relative Deviation,RD)得到模型值偏离测量值的实际大小,表达式为:

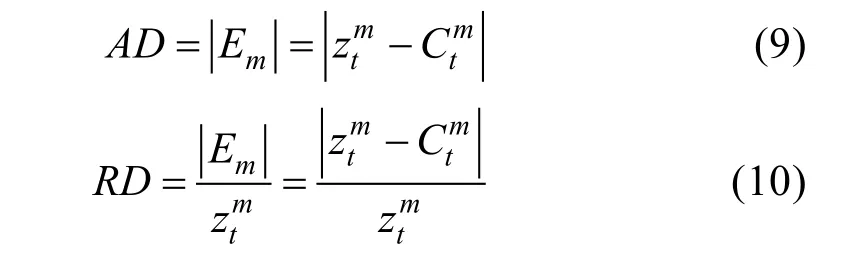
其中,模型值表示为,测量值表示为,m表示样本个数且1≤m≤P,P表示全部样本个数,t表示向量为输出参数,同时表示输出参数的个数,在本文中,t=1。

为了比较不同时延的历史数据对模型的影响,本文计算不同时延下两个模型的评估参数,包括RMSE、MAE 以及LC,结果如图6 所示。由图可知,随着时延的增加,多元线性回归模型的RMSE和MAE 与BP 神经网络模型的RMSE 和MAE 都在增加,多元线性回归模型的LC 与BP 神经网络模型的LC 在不断减小,这是由于随着时延的增加,历史数据与对流电场的相关性在减弱,说明随着时延的增加,两种模型的性能在变差。对比两个模型不同时延的多元线性回归模型和BP 神经网络模型的RMSE、MAE 和LC 的大小,可以看到多元线性回归模型在时延较小时性能比BP 神经网络模型的性能略好,但是随着时延的增加,两个模型的RMSE 和MAE 趋于相等,而二者的线性相关系数差距拉大,表明BP 神经网络模型的性能随着时延的增大逐渐优于多元线性回归模型。

图6 不同时延下SuperDARN 测量值与多元线性回归模型预测值(蓝色)和BP 神经网络模型预测值(棕色)的均方根误差RMSE(a)、平均绝对误差MAE(b)和线性相关系数LC(c)Fig.6.a) The root mean square error (RMSE),b) the mean absolute error (MAE) and c) the linear correlation coefficient (LC) of SuperDARN measured values and predicted values of multivariate linear regression model (blue) and predicted values of BP neural network model (brown) at different time delays

随时延的增加,直到约20 分钟,模型的预测性能基本不再变化,这与太阳风能量耦合到电离层所需时间为几十分钟的量级基本一致。由于磁层-电离层对太阳风能量的响应有几十分钟到几个小时的滞后[24],Bargatzed 等[25]使用线性预报滤波技术分析了太阳风资料和极光地磁活动指数AL 的相关关系,发现磁层-电离层对太阳风响应的滞后相关曲线有两个高峰,一个为20 分钟,一个为60 分钟。而在时延20分钟之后的RMSE 和MAE 基本不再变化,逐渐趋于稳定,故在此选择时延为20 分钟的历史数据构建电场模型。

图7a 显示了不同模型预测的对流电场随时间的变化情况,其中SD 代表SuperDARN 的测量值,MLR 和BPNN 分别代表多元线性回归模型和BP 神经网络模型计算结果。图7b 和7c 分别给出了不同模型预测的对流电场与SuperDARN 测量值之间的绝对误差和相对误差 随时间的变化情况。正误差表示模型预测的是较小的值,而负误差表示模型预测的是较大的值。总体而言,多元线性回归模型和后向传播神经网络预测的对流电场与 SuperDARN 测量的对流电场变化总体趋势很接近,所以这些曲线重合地方较多。绝对误差主要在-5～+5 mV·m-1范围内,相对误差主要在-20%～20%之间。在个别处存在一些较大的误差。

图7 不同模型预测情况及模型误差分析.a)SuperDARN 测量(绿色曲线)、多元线性回归模型预测(红色曲线)和BP 神经网络模型预测(蓝色曲线)的电场随时间的变化; b)电场的绝对误差变化,红色曲线表示SuperDARN 测量与多元线性回归模型之间的误差,蓝色曲线表示SuperDARN 测量与BP 神经网络模型之间的误差; c)电场的相对误差变化,曲线含义同b)Fig.7.The prediction results of different models and their error analysis.a) variations of the electric field with time for SuperDARN measurement (the green curve),the predicted values of multivariate linear regression model (the red curve) and the predicted values of BP neural network model (the blue curve).b) the absolute error variations of electric field.The red curve represents the errors between SuperDARN measurement and the predicted values of multivariate linear regression model.The blue curve represents the errors between SuperDARN measurement and the predicted values of BP neural network model.c) the relative error variations of electric field.The meanings of curves are the same as those in b)

绝对误差和相对误差直方图分布以及高斯拟合图像如图8 所示。图8a 表示多元线性回归模型的计算值和测量值的绝对误差的直方图用高斯函数拟合的结果,均值μ=-0.098,方差σ=2.579。如图8b 所示,相对误差分布也非常接近高斯分布,μ=0.007,σ=0.152。图8c 表示BP 神经网络模型的计算值和测量值的绝对误差的直方图,及用高斯函数拟合的结果,μ=0.394,σ=2.534。如图8d 所示,相对误差分布同样非常接近高斯分布,μ=0.035,σ=0.146。将两个模型绝对误差和相对误差的μ和σ进行对比,BP 神经网络模型的绝对误差和相对误差的σ较小。此外,BP 神经网络模型的误差分布更窄,同时峰值也略大于多元线性回归模型,表明BP 神经网络算法对于电离层电场模型的构建具有明显的优势。

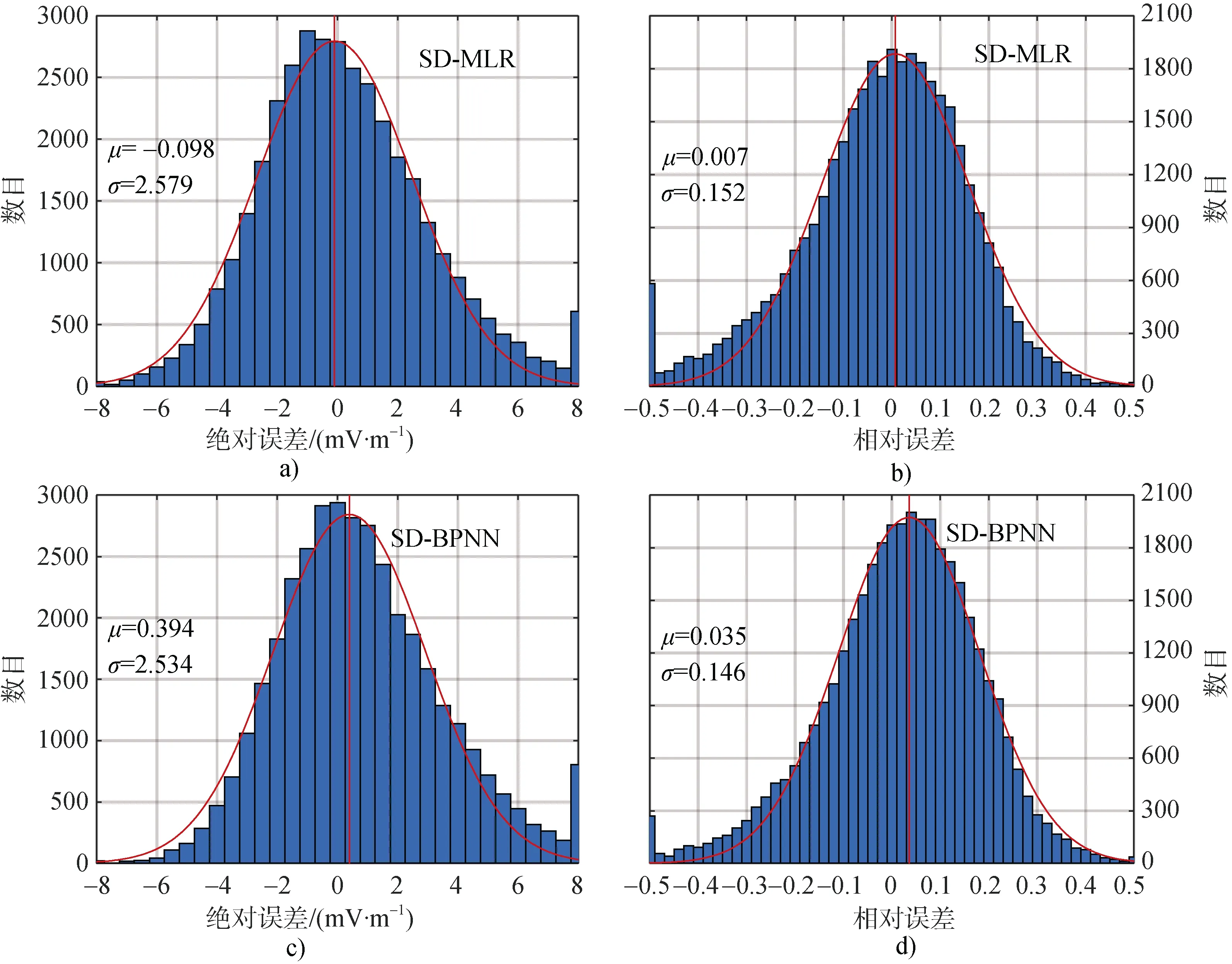
图8 SuperDARN 测量与多元线性回归模型和BP 神经网络模型预测的电场值的绝对误差和相对误差直方图分布.SuperDARN 与多元线性回归模型的绝对误差(a)和相对误差(b); SuperDARN 模型与BP 神经网络模型的绝对误差(c)和相对误差(d)。红色曲线为高斯拟合,红色垂直直线为拟合的平均值Fig.8.The absolute and relative error histogram distributions of the electric field between the SuperDARN measurements and the predicted values of multivariate linear regression model and BP neural network model.The absolute errors (a) and relative errors (b) between SuperDARN datasets and multivariate linear regression model.The absolute errors (c) and relative errors (d) between SuperDARN datasets and BP neural network model.The red curves are Gaussian fitting,and the red vertical straight lines are the mean values of the fitting.

本文从RMSE、MAE 和LC 三个参数定量分析评估两个模型。其中,RMSE 和MAE 主要用于衡量误差的大小,而LC 则是对预测值和测量值之间的拟合程度进行评估。根据图9a 所示,对于多元线性回归模型,RMSE、MAE 和LC 的性能指标分别为 3.15 mV·m-1、2.39 mV·m-1和0.7 2。根据图 9b,对于 BP 神经网络模型,RMSE、MAE 和LC 的性能指标分别为3.31 mV·m-1、2.47 mV·m-1和 0.77 。图9c描绘了来自SuperDARN 测量和模型预测的对流电场的分布。显然,BP 神经网络模型预测结果与SuperDARN 测量结果分布相近,对于较小的值预测比较准确,对于较大的值预测的结果偏小,而多元线性回归模型对于较大和较小的值预测结果都偏小。

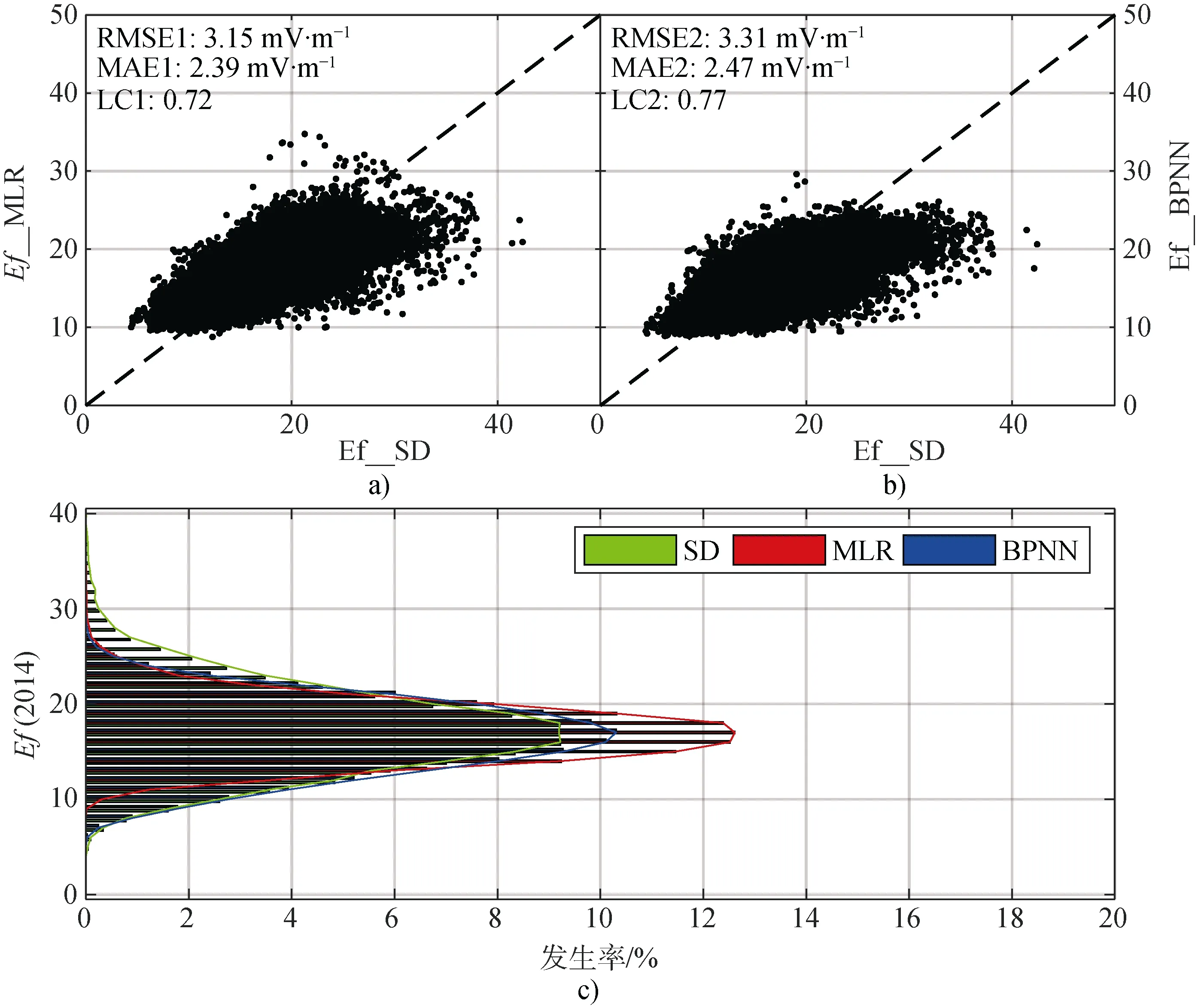
图9 a)SuperDARN 测量值与多元线性回归模型预测值; b)BP 神经网络模型预测值的均方根误差、平均绝对误差和线性相关系数; c)SuperDARN 测量(绿色)、多元线性回归模型(红色)和BP 神经网络模型(蓝色)输出的对流电场的分布Fig.9.The root mean square error RMSE,the mean absolute error MAE and the linear correlation coefficient LC of the electric field between SuperDARN and models using multivariate linear regression analysis (a) and BP neural network algorithm (b); c) the occurrence distributions of the electric field obtained from SuperDARN measurements (green),multivariate linear regression model (red) and BP neural network model (blue).

综合判断,BP 神经网络的线性相关度高,预测结果同SuperDARN 测量结果更加相近。因此,该结果证明了深度学习算法在极区电离层对流电场模型构建和预测中的有效性。

4 讨论与结论

由于极区电离层对流受到太阳风-磁层-电离层中的电动力学过程的影响,电离层对流电场的变化规律和太阳风和IMF 以及地磁活动均有着密切的关系。Thomas 等[26]验证了对流电场与风暴增强密度(SED)的中纬度羽流形成的舌状电离层(TOI)的关系,证明了对流电场在中纬度SED 产生TOI 中的控制作用。Xu 等[27]统计比较了DMSP速度矢量和SuperDARN 对流矢量,结果表明由于两种仪器时空分辨率的差异以及SuperDARN雷达后期数据处理方法的不同导致SuperDARN测量的速度在对流较强时明显低于DMSP 卫星观测速度。对于跨极盖电势的研究,Bristow 等[12]构建了基于太阳风速度、行星际磁场以及时钟角组成的 CPCP 模型,其形式为CPCP=42.956+ 9.08VBsin3(θ/2),其中V表示太阳风速度,B表示行星际磁场IMF,θ是IMF 时钟角,该模型引入的均方根误差为13.45 kV,线性相关系数为0.61。 Koustov 等[15]分析了CPCP 随着Ekl的变化关系,提出了CPCP 与三者的指数关系形式为CPCP(x)=P-S×exp(-(x/T)),其中x代表不同的输入参数,包括行星际电场,Ekl以及PCN 指数。P,S,T分别为不同输入时进行最佳拟合得到的系数。该模型引入的误差最小为11.87 kV。在本研究中,利用数据集中的最大电势点与最小电势点的经纬度计算得到距离d,与模型输出的对流电场的预测值反推跨极盖电势差CPCP 后,与CPCP 测量值进行了对比。本文所使用的多元线性回归模型和BP神经网络模型其误差RMSE 分别为10.33 kV 和9.94 kV,LC 分别为0.61 和0.66,与已有模型相比模型质量均有所提升。所以综合RMSE 和LC 两个参数,本文使用的BP 神经网络模型的预测性能最好,而前人的几个基于统计算法引入的模型,误差均较大。该结果也证明了BP 神经网络算法在对流电场的非线性建模及预测中的有效性和准确性。

本文中,基于SuperDARN 电离层对流数据,得到了跨极盖电势差CPCP 和跨极盖电场值Ef,通过深度学习算法构建了电场模型并对其进行了评估。结果显示了深度学习算法在非线性模型构建中的优势,对于空间天气模型的构建具有一定的借鉴作用,具有广泛的应用前景。

但是,在电离层对流电场的模型化过程中,如何选取合适的近地空间参量是一个较为复杂的工程,而且,深度学习算法中输入参数的数目应与日地系统中发生的物理过程相对应,并应受到足够的限制,以避免网络过载,从而能够适应大数据量的训练并尽量缩短训练时间。在未来在利用深度学习构建电离层对流及对流电场模型时,还应综合考虑其他参数,如地磁指数Kp、太阳风参数的优化组合、时钟角、关联度较高的函数阶数等参数[28]。

基于2014年的SuperDARN 的测量数据,本文研究了对流电场与电离层等离子体对流的各种参数的关系,得出了以下结论:

(1)结果表明IMFBz分量、太阳风电场Esw、AE 指数和Kan-Lee 重联电场Ekl与对流电场密切相关。

(2)引入历史数据使得构建的电场模型更加精确,并通过不同时延下模型的RMSE、MAE 和LC 的比较,得到时延20 分钟是最佳历史电场数据,并使用该时延的历史数据构建模型。

(3)结合四个强相关参数以及历史数据,提出了基于BP 神经网络的深度学习模型和多元线性回归模型。通过对两个模型的验证和测试,结果表明SuperDARN 测量值和两个模型的结果的误差均在合理范围内。对于多元线性回归模型,RMSE、MAE 和LC 的性能指标分别为3.15 mV·m-1、2.39 mV·m-1和0.72; 对于BP 神经网络模型,RMSE、MAE 和LC 的性能指标分别为3.31 mV·m-1、2.47 mV·m-1和0.77。SuperDARN 测量和BP 神经网络模型预测的对流电场的分布近似,同时BP 神经网络的线性相关度高。

从误差、相关度和预测结果分布三个方面来看,BPNN 模型具有良好的非线性建模、分析和预测能力。因此,该结果证明了深度学习算法在极区电离层对流电场模型构建和预测中的有效性。

致谢本文感谢弗吉尼亚理工学院暨州立大学提供的 SuperDARN 数据,该数据从SuperDARN 官方网站(http://vt.superdarn.org/)免费获得。SuperDARN 是由澳大利亚、加拿大、中国、法国、意大利、日本、挪威、南非、英国和美国的国家科学基金机构资助的雷达集合。同时感谢NASA/GSFC 提供的OMNIWeb 服务和OMNI 数据。非常感谢编辑和审稿人的建议和意见。