近断层地震作用下拉索模数伸缩缝对斜交桥地震响应的影响研究

劳天鹏，高贵，党新志，练强，张鹏辉，袁万城

(1.同济大学 桥梁工程系，上海200092；2.武九铁路客运专线湖北有限责任公司，湖北 武汉430200)

我国的高等级公路上，斜交桥的数量一般可以达到整条线路桥梁总数的40%～50%[1]。斜桥由于在地震中容易发生产生平面内旋转，导致主梁锐角处发生较大的位移，并且可能引起支座脱落[2]。近断层脉冲型地震动在长周期段较非脉冲地震具有更大的反应谱值，对桥梁结构具有更高的抗震需求[3]。1994年Northridge后的震害调查发现，斜桥的斜度越大，绕竖轴产生的转动越大，越容易落梁，在近断层区域该效应尤其显著[2]。MAN‐GALATHU等[4]利用易损性曲线研究得出，桥点距离断层越近，斜度越大，斜交桥危险性也就越大，并对此提出了风险修正系数。王军文等[5]研究发现横向挡块能够降低梁端纵向最大位移、主梁峰值转角。WEI等[6−7]编程计算对摩擦减隔震装置的性能做了详细的讨论，分析地震特性对滚动摩擦系统的位移响应的影响。本文提出采用拉索模数伸缩缝改善斜交桥在近断层地震作用下的抗震性能，介绍了拉索模数伸缩缝的力学本构关系以及其控制斜交桥旋转的机理，并以一座3 m×30 m的连续斜交梁桥为例建立有限元模型，输入实测的脉冲型近断层地震动记录，比较不同地震动输入角度、斜度下斜交桥的抗震性能，研究拉索模数伸缩缝对斜交桥抗震性能的影响。

1 拉索模数伸缩缝

1.1 工作原理

拉索模数伸缩缝是在传统的模数伸缩缝上，用贯穿的拉索组件将两端的支撑箱体与支撑横梁连在一起，图1为拉索模数伸缩缝示意图。拉索具有一定的自由程，两端的梁体或桥台相对位移小于自由程，拉索不发挥作用，满足正常的温度变化、车辆冲击的变形要求。若其相对位移大于拉索的自由程，当两端的梁体或桥台相互靠近时，拉索将限制其进一步的靠近，避免碰撞；当两端的梁体或桥台相互远离时，拉索限制两端位移进一步扩大，避免落梁[14]。

图1 拉索模数伸缩缝构造及本构关系Fig.1 Structure of cable-module expansion joints

拉索模数伸缩缝的本构关系如图2所示，其力与位移关系为：

图2 拉索模数伸缩缝本构模型Fig.2 Constitutive model of cable-module expansion joints

其中，Δ为拉索模数伸缩缝两端发生的相对位移；F为拉索模数伸缩缝的回复力；Kc为拉索模数伸缩缝刚度；D为拉索模数伸缩缝自由程。

1.2 斜交桥旋转机理

斜交桥由于主梁与桥台的碰撞导致主梁的旋转[12]，如图3(a)所示，当碰撞产生时，由于桥台对主梁碰撞力的合力方向与主梁的刚度中心不在同一直线上，会导致主梁平面内的旋转，这种旋转将引起锐角边出现过大的位移，最终导致落梁。

拉索模数伸缩缝改变了水平方向主梁梁端与桥台的无约束状态，通过设置合适的拉索模数伸缩缝自由程，使拉索在主梁与桥台发生碰撞之前受力，对主梁产生约束作用，如图3(b)所示。在主梁与桥台靠近端，拉索模数伸缩缝限制其靠近，产生推力；在主梁与桥台远离端，拉索模数伸缩缝限制两端位移扩大，产生拉力。推力与拉力是相同的，其合力方向与主梁的刚度中心在同一直线上，有效地避免了主梁的旋转。当地震输入方向不与桥轴线平行时，主梁横向运动与桥台碰撞会产生旋转，由于主梁旋转过后各角点与桥台的相对位移不同，拉索将产生不同大小的力，如图3(c)所示，在锐角点处，拉索模数伸缩缝产生拉力，限制其进一步地远离，拉索模数伸缩缝产生与旋转方向相反的扭矩，使主梁旋转得到控制。

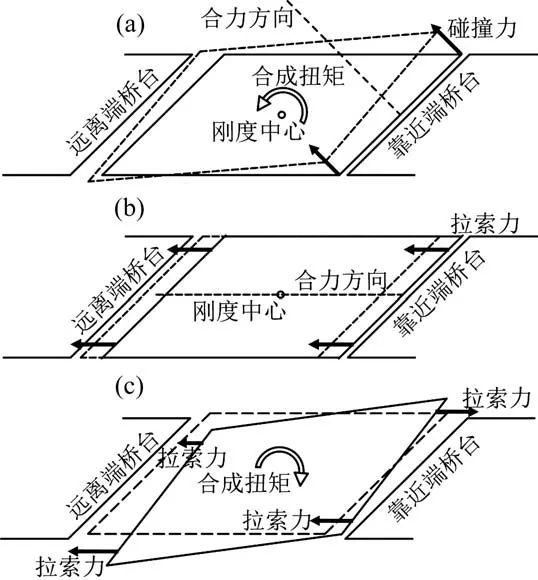
图3 斜交桥的碰撞效应Fig.3 Pounding effect of skew bridge

2 有限元模型

2.1 模型概况

本文以一座跨度为3 m×30 m的钢筋混凝土斜交连续梁桥为例建立有限元模型。主梁为4片C50混凝土预制小箱梁，梁高1.6 m，单个箱梁宽3.5 m，箱梁之间采用湿接缝拼接；桥墩处支座采用板式橡胶支座，桥台处支座为滑板式橡胶支座，支座布置如图，板式橡胶支座与混凝土之间的摩擦因数取0.2，滑板式橡胶支座摩擦因数取0.06[9]；桥墩为C40混凝土双柱框架墩，墩高10 m，墩柱为1.6 m×1.6 m的实心截面；两侧桥台均为桩柱式桥台，桥台高2.8 m，宽15 m。

使用SAP2000程序建立全桥有限元模型(如图4)。与精细化有限单元模型相比，简化的单梁模型既能保证较好的计算准确性，又能减少计算量[10]。由于地震过程中主梁基本保持弹性，故采用弹性梁柱单元模拟。支座采用PlasticWen单元模拟，考虑支座的滑动，支座其最大剪力为摩擦力，因此桥墩在地震作用下一直保持弹性，故桥墩采用弹性梁柱单元模拟。考虑桩土相互作用影响，采用M法计算群桩基础6个方向的刚度，并分别赋予土弹簧的6个方向。桥台为重力式桥台，在有限元模型中固结于地面。

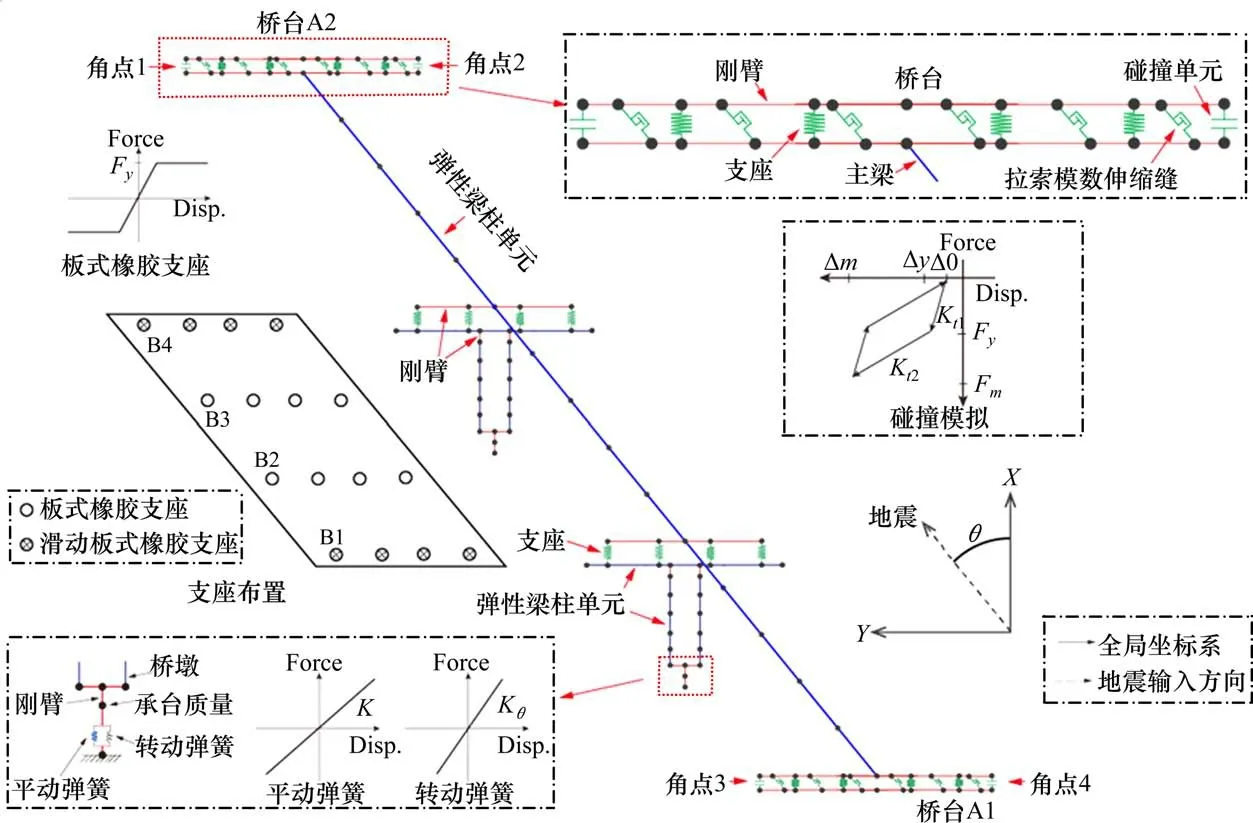
图4 有限元计算模型Fig.4 Finite element calculation model

在梁截面的最外缘各设置一个碰撞单元模拟斜交桥的碰撞效应[11]，桥台碰撞单元采用何健等[12]的计算方法，碰撞单元刚度取为梁体轴向刚度的1/10，在梁截面的最外缘各设置一个，方向垂直于梁端截面，碰撞单元初始缝隙根据桥台处伸缩缝缝宽取10 cm。拉索模数伸缩缝的拉索布置间距1.2 m，梁端各布置12根拉索，拉索刚度由拉索弹性模量、拉索直径等决定，自由程也可以根据实际需要调整[14]，本文刚度Kc取10 000 kN/m，拉索自由程D取0.06 m。为简化建模计算，模型中将相邻2个拉索模数伸缩缝单元合并为一个，因此模型梁端各设置6个拉索模数伸缩缝单元，方向平行于主梁单元。

2.2 近断层地震动时程选取

本文从美国太平洋地震工程研究中心(PEER)的数据库选取了实际地震中记录下的3条近断层地震波。为了便于比较，本文将地震动的峰值加速度(PGA)统一调整为0.2g。调整后的地震波加速度反应谱如图5。近断层地震的脉冲特性主要由断层破裂过程中的破裂前方向效应和滑冲效应造成，在反应谱中表现为长周期段的较非脉冲地震有更大的谱值[3,15]。表1列出了地震动的详细参数，脉冲持时为BAKER[13]利用小波分析处理地震动记录，分解出脉冲得到的定量指标。

表1 选用的地震波Table 1 Selected seismic waves

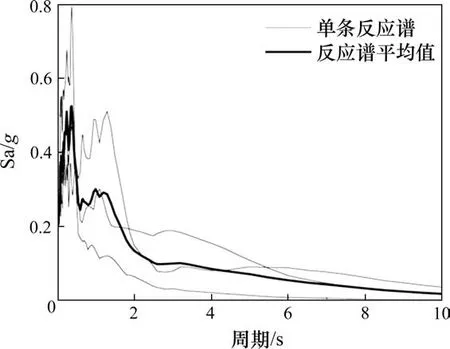
图5 选用的地震动加速度反应谱Fig.5 Selected seismic response spectrum

3 地震响应分析

3.1 地震动输入角度的影响

对于不同的激励方向，斜交桥的地震响应有较大差异，需要考虑最不利地震动输入方向问题。本文比较了地震动输入方向对结构地震响应的影响，桥梁斜度30°，地震动输入角度按全局坐标轴X方向(垂直于桥台方向)为起始方向逆时针旋转，每隔10°输入计算一次，对3条近地震动的结果取平均值。

主梁旋转导致落梁是近断层地震斜交桥震害的典型特征[2]，图6显示了主梁在不同地震动输入角度下的最大旋转角，图中“-N”表示没有采用拉索模数伸缩缝，“-Y”表示采用了拉索模数伸缩缝，在本文图表中均按此方法标注。没有拉索模数伸缩缝时，斜交桥最大转角位0.21°，出现在地震沿20°方向输入的时候。随着地震输入角度增加，主梁转角减少，在Y轴方向(平行于桥台方向)，转角接近于0，也就是没有发生转动。这是因为平面转动振型的振型参与系数Y方向分量很小，所以Y方向激励时，不能激励起转动的振型，同时主梁沿着Y轴平动，也不能发生碰撞，引发旋转；当地震输入角度超过90°，继续增加时，主梁转角又重新增加。结构响应随地震输入角度的变化规律有对称性，地震沿着θ°输入时结构的响应和地震沿着θ+180°输入时大小相等，方向相反，后面的计算都是类似的情况。有拉索模数伸缩缝时，最大转角的数值减小为0.047°，在地震沿着150°方向输入时发生。拉索模数伸缩缝存在时，能使得主梁转角减少78%以上，这表明拉索模数伸缩缝能有效的减少主梁的旋转。

图6 主梁最大转角和近断层地震输入角度的关系Fig.6 Relationship between the maximum angle of main beam and the incident angel of near-fault earthquake

图7 和图8显示了斜交桥B1，B2，B3和B4支座(支座位置见图4)在不同地震动输入角度下纵桥向位移(X轴方向)和横桥向(Y轴方向)位移。B1，B2，B3和B4支座沿着主梁从钝角一端排列到锐角端，支座的纵向和横向位移逐渐增大，说明地震作用下主梁绕着钝角转动。在不同地震动输入角度作用下，拉索模数伸缩缝均能减小支座位移。对于中间墩B2和B3支座，拉索模数伸缩缝能有效减小纵向位移；对于桥台的B1和B4支座，拉索模数伸缩缝能有效减小支座纵桥向和横桥向的位移；在地震沿着X方向输入时，拉索模数伸缩缝对支座横位移的限制作用尤其明显；这表明近断层作用下，拉索模数伸缩缝能很好的预防防止落梁发生。

图7 支座纵向位移和近断层地震动输入角度的关系Fig.7 Relationship between the longitudinal displacement of bearing and the incident angel of near-fault earthquake

图8 支座横向位移和近断层地震动输入角度的关系Fig.8 Relationship between the lateral displacement of bearing and the incident angel of near-fault earthquake

桥墩在地震作用下受到的作用力主要有自身的惯性力和上部结构通过支座传递到墩顶的摩擦力，有无模数伸缩缝不改变桥墩自身的惯性力，由以上讨论可以得知模数伸缩缝存在时减小了支座位移和内力，也就减小了上部结构传递到桥墩的内力。因此，模数伸缩缝存在时，桥墩的地震内力反应也会减小。

3.2 斜度对地震响应的影响

斜度是影响斜交桥地震响应的主要参数[2,7]。本文先利用软件SAP2000建立了不同斜度斜交桥的有限元模型，斜度分别为0°(直桥)，15°，30°，45°和60°，保持跨径(主梁长度)不变，比较其振动特性。

表2 为不同斜度的斜桥的第一阶振型和平面旋转振型对应的周期和振型质量参与系数。不同斜度的斜交桥第一阶振型都是主梁沿着Y轴平动，这是因为主梁质量没有改变，横向刚度主要由支座决定，而支座刚度也没有改变。主梁的平面转动都是第3阶振型。对不同斜度的斜交桥，沿各个方向输入近断层地震动，最大转角随着近断层地震输入角度变化的规律如图9所示。

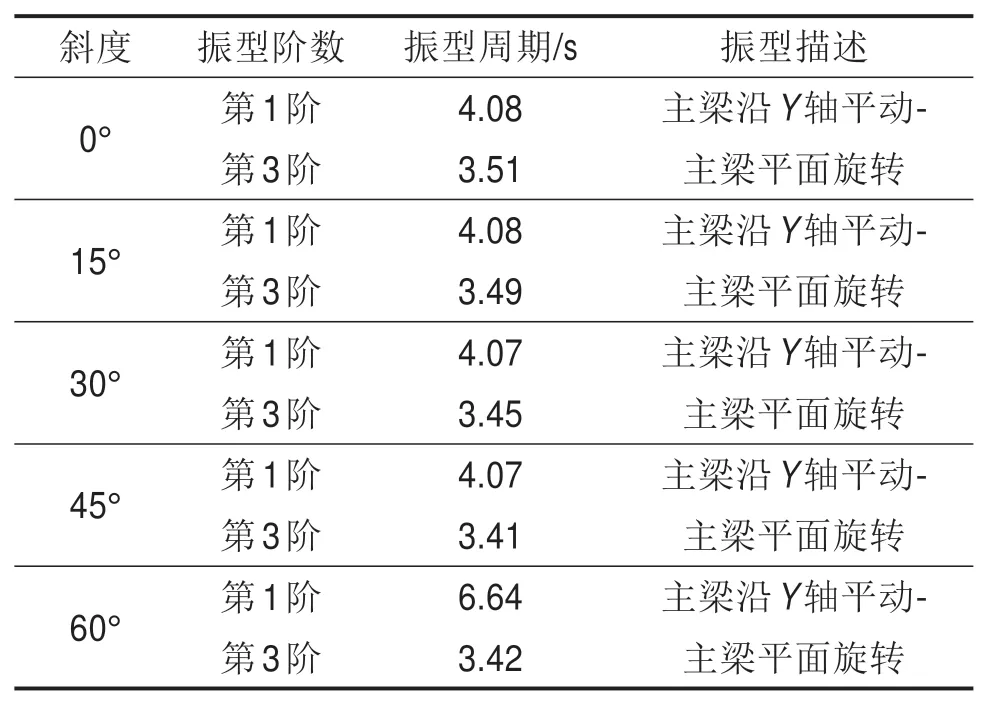
表2 不同斜度斜交桥振型及周期Table 2 Modal shape and period of skew bridges with different skewness

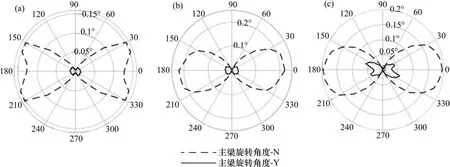
图9 不同斜度的斜交桥主梁最大转角和近断层地震输入角度的关系Fig.9 Relationship between the maximum angle of main beam and the incident angel of near-fault earthquake for skew bridges with different skewness

计算结果表明：不同斜度的斜交桥在近断层地震作用下，主梁最大转角随地震输入角度变化规律类似，地震在纵桥向及附近30°范围内输入时，主梁转角最大。地震在横桥向输入时，主梁转角最小，接近于0，说明主梁在横向地震作用下主要发生平动；对于不同斜度的斜交桥，不同的地震输入角度，拉索模数伸缩缝存在时，主梁平面转动都明显减少。

4 结论

1)在近断层地震不同的输入角度下，拉索模数伸缩缝均能有效减小主梁的平面旋转角度，进而限制主梁位移和支座位移，有效防止近断层地震作用下落梁发生。

2)对于中间墩的支座，拉索模数伸缩缝能有效减小纵桥向位移；对于桥台的支座，拉索模数伸缩缝能有效减小纵桥向位移和横桥向位移。

3)不同斜度的斜交桥在近断层地震作用下，主梁最大转角随地震输入角度变化的规律基本一致，在纵桥向附近输入时转角最大，在横桥向输入时转角接近于0。

4)对于不同斜度的斜交桥，拉索模数伸缩缝均能有效发挥限位作用，减小主梁平面转动，防止落梁发生。