高速铁路高架桥区段接触网避雷线架设高度研究

王思华，王宇，李萍，陈天宇

(1.兰州交通大学 自动化与电气工程学院，甘肃 兰州730070；2.甘肃省轨道交通电气自动化工程实验室(兰州交通大学)，甘肃 兰州730070)

接触网是高速列车运行的电力来源，然而裸露在自然环境中的接触网没有后备，一旦出现故障，将会影响高速铁路的安全运行，造成重大经济损失。雷击引起的接触网跳闸事故占到总跳闸事故的30%以上。由于地形因素，我国高速铁路接触网多数路段架设在高架桥上，相对普铁增加了对地高度，更容易遭受雷击[1]。而大部分接触网仅在关键部位设置了避雷器来限制雷电过电压[2]。国内外针对接触网防雷做出了大量研究，AOD‐SUP等[3]对避雷线的位置进行了优化，找到了理想的屏蔽角。周利军等[4]分析了现有高速铁路防雷体系的缺陷，并利用电气几何模型和实测数据分析无避雷线时高速铁路牵引供电系统的雷击特性。卢泽军等[5]基于电气几何模型，计算了高架桥接触网引雷范围。边凯等[6]提出在接触网绝缘子旁并联安装带间隙避雷器，沈海滨等[7]采用实验模拟的方法研究工频电弧灼烧绝缘子，论证了接触网复合绝缘子的防雷特性。XIANG等[8]分析影响牵引供电系统雷击风险的组成因素,基于解耦法建立了高速铁路高架桥雷电电磁暂态模型。此外，HAYAS‐HIYA等[9]提出了一种利用广角镜评估接触网系统防雷状况的新方法。我国高速铁路在雷电活动频繁的地区采用架设专用避雷线的方法保护接触网，避雷线的高度设计至关重要[10−11]。高速铁路多用高架桥敷设，当前对高架桥区段的接触网架设避雷线高度与高架桥高度之间的关系研究较少。专家学者们重点对避雷线的架设方式及耐雷性能进行了研究，很少详细分析避雷线的高度。本文从电气几何模型和滚球法2种计算方法来求得两者的联系，并得出相应高架桥高度下合适的避雷线架设高度。

1 高架桥区段接触网的结构参数

我国高速铁路以AT供电方式为主，AT供电方式主要有供电能力强，供电距离远，电能损耗小等优点。图1为某高速铁路高架桥区段接触网的结构示意图，一般的桥面离地面的距离为10 m或12 m甚至更高。图中主要包括朝向田野侧的馈线F和朝向轨道内侧的承力索及下方的接触线T。雷电入侵时主要对F线和T线造成损害，由于承力索与T线之间存在吊弦视为联合导线。

图1 高速铁路高架桥区段接触网结构Fig.1 Catenary structure of high-speed railway viaduct section

2 接触网避雷线架设高度计算方法

2.1 电气几何模型

电气几何模型(EGM)[12−13]是能够预测雷电与大地、导线之间击距关系的经典模型，常用于输电线路上计算导线受雷击情况。高速铁路接触网导线与输电线路架设方式不同，但是也可以用电气几何模型分析雷击接触网。高架桥增加了导线对地高度，避雷线架设的高度也会受到影响，需要根据桥的高度结合电气几何模型对避雷线的架设高度进行计算。以下分别为单线和复线铁路2种情况下的避雷线架设高度计算方法。

2.1.1 单线情况

如图2所示，高架桥区段的接触网架设避雷线后的保护范围为弧AB，弧AB完全屏蔽F线和T线受雷击时即为避雷线架设的最佳高度。按照图2对避雷线的高度进行求解，分别求出完全屏蔽T线和F线的避雷线高度，取两者最大值为最佳避雷线高度。根据经典电气几何模型的击距公式，可知Rs，Rc和Rg为：

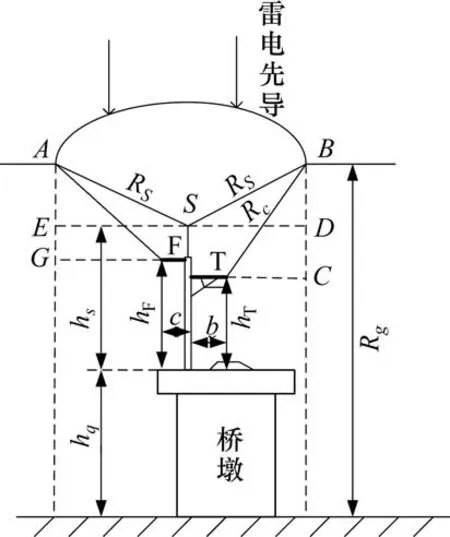
图2 单线情况的接触网避雷线架设高度(电气几何模型)Fig.2 Erection height of catenary lightning protection wire in single line(EGM)

对于T线，在三角形BDS和BCT中，

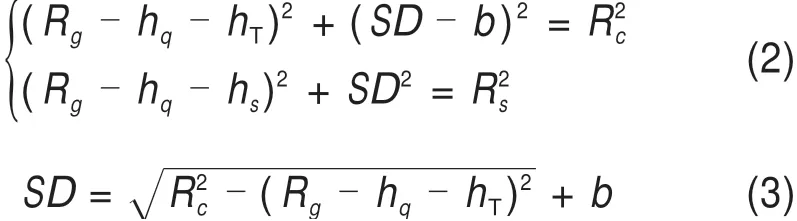
由以上公式可得，对于T线，接触网避雷线架设高度计算公式为：

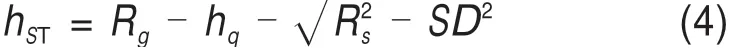
同理可得，对于F线，接触网避雷线架设高度计算公式为：

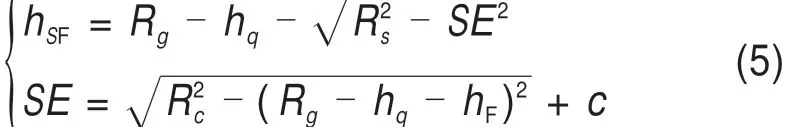
式中：Rs，Rc和Rg分别为避雷线、导线、大地的击距；I为雷电流幅值；hq为高架桥高度；hT，hF分别为T线和F线离桥面的高度；b，c分别为T线和F线到支柱的水平距离。

2.1.2 复线情况

高架桥区段复线运行时接触网架设避雷线后的保护范围如图3所示，两边支柱架设避雷线后屏蔽范围关于AG中心对称，只需要对图3左边的接触网避雷线高度计算即可。T线距离中心线AG的横向距离为a，由三角形ACS和ADT得：

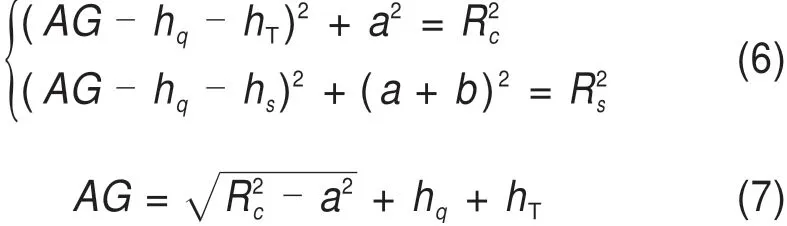
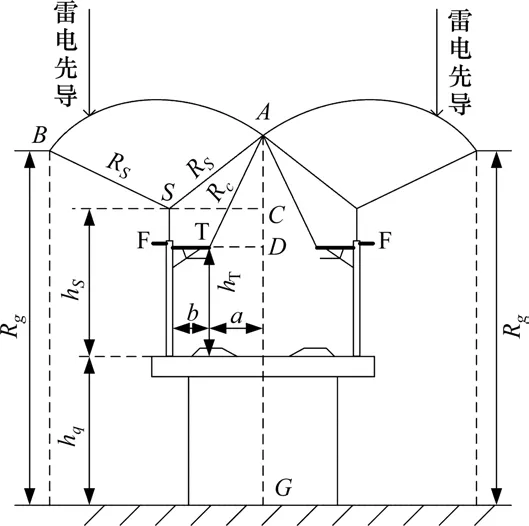
图3 复线情况的接触网避雷线架设高度(电气几何模型)Fig.3 Erection height of catenary lightning protection wire in double line(EGM)

计算得屏蔽T线的避雷线高度为：

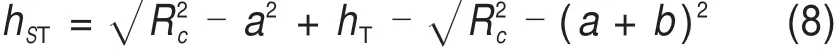
由式(8)可知，只考虑T线时避雷线架设高度与高架桥高度hq并无关联。分析图3发现，考虑F线时，计算方法同单线情况一致，计算公式同式(5)。

2.2 滚球法

滚球法的原理是以某一规定半径的球体做滚动，某些建筑物上装有接闪器，当滚动时遇到接闪器无法触碰到一些范围，这些范围就是接闪器能够保护到的范围[14−15]。滚球法是国际电工委员会(IEC)推荐的接闪器保护范围计算方法之一，具有计算方法简单，计算量小等优点，对于高架桥区段避雷线的保护范围计算同样适用。下面对单线和复线铁路的高架桥接触网避雷线架设高度计算方法分别进行分析。

2.2.1单线情况

如图4所示，以R为半径的球体从左边远方地面运动，避雷线保护范围使得此球体刚好触碰到F线，即为F线在避雷线的保护范围内，此时可以计算出保护F线的避雷线最低高度h1；同理，计算出保护T线的避雷线最低高度h2。取两者的最大值确保F线和T线都能受到避雷线的保护。由三角形O1AS和O1BF得：

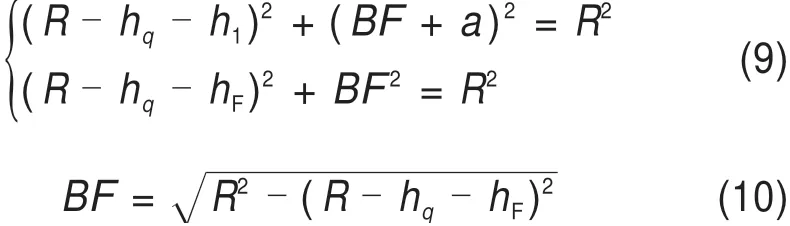
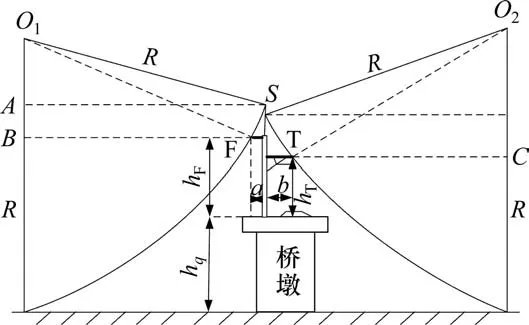
图4 单线情况的接触网避雷线架设高度(滚球法)Fig.4 Erection height of catenary lightning protection wire in single line(Rolling ball method)

由式(9)得：

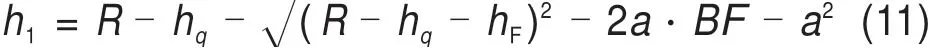
同理得：

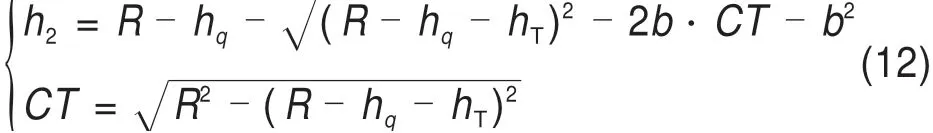
2.2.2 复线情况

采用滚球法按照圆心O1，O3和O2滚动，保护范围如图5所示。轨道内侧的T线已完全受到避雷线的保护，此时只需要对F线进行保护。由于两侧的接触网及保护状态关于O3G中心对称，针对F线计算一侧的避雷线架设高度即可。同理可得复线情况下的避雷线高度为：

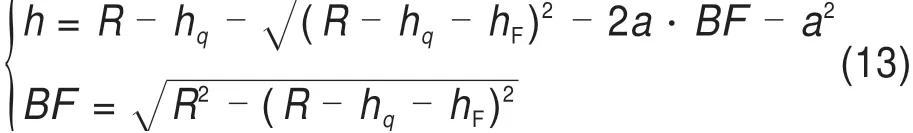
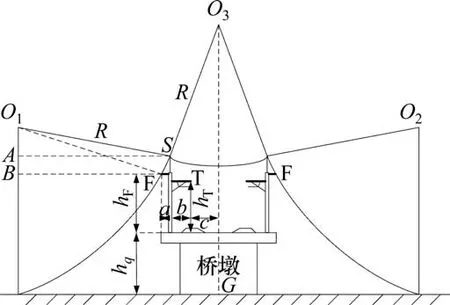
图5 复线情况的接触网避雷线架设高度(滚球法)Fig.5 Erection height of catenary lightning protection wire in double line(Rolling ball method)

3 2种方法的计算结果

3.1 采用电气几何模型的计算结果

根据相关文献的防雷要求，要避免10 kA以上的雷电直击接触网和承力索[16]。因此可以按10 kA的雷电流对避雷线的高度进行计算。将雷电流幅值及相关的参数代入公式中，计算的单线线路避雷线架设高度如表1所示。

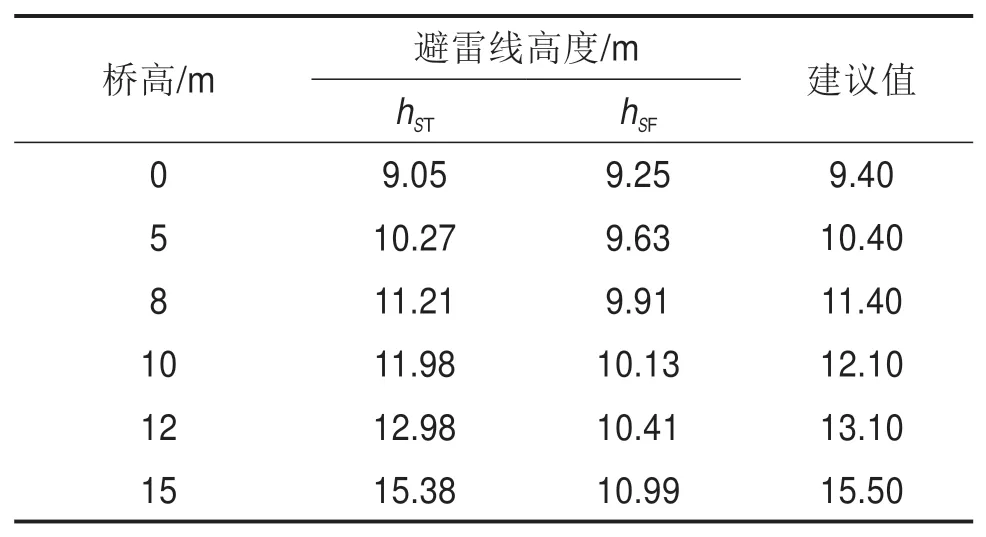
表1 单线线路避雷线高度(电气几何模型)Table 1 Lightning wire height of single-track lines(EGM)

复线线路依照上述计算方法，式(8)已经得到了T线完全受保护时的避雷线高度，重点对F线进行分析即可。计算得到的避雷线高度如表2。

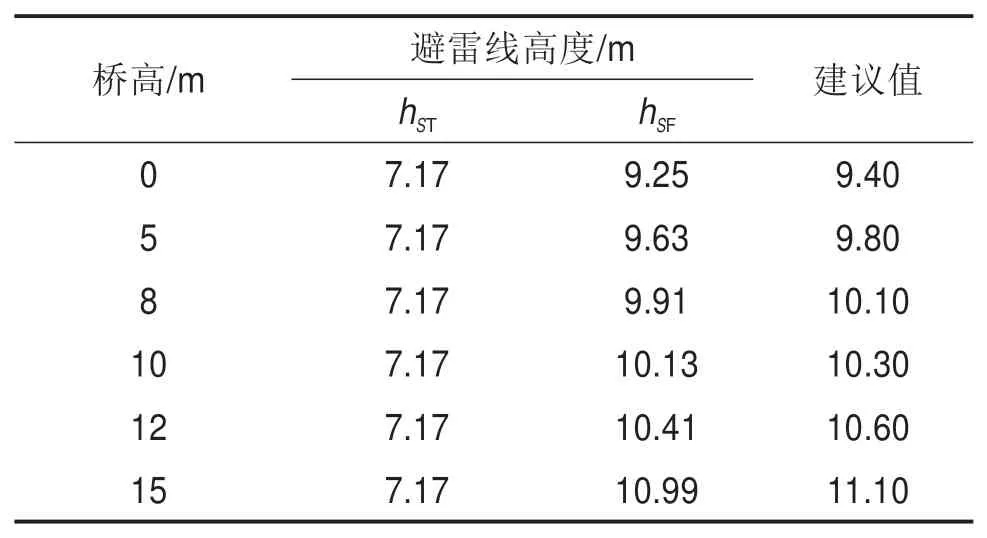
表2 复线线路避雷线高度(电气几何模型)Table 2 Lightning wire height of double-track lines(EGM)

3.2 采用滚球法的计算结果

按《建筑物防雷设计规范》GB50057—2010的规定，建筑物应根据其重要性、使用性质、发生雷电事故的可能性和后果，按防雷要求分为3类，此3类的滚球半径分别为R1=30 m，R2=45 m，R3=60 m。高速铁路接触网属于重要设备，选用滚球半径为45 m计算避雷线的高度。由于复线时只需要考虑保护F线，依据滚球法将计算的单线和复线避雷线高度见表3。

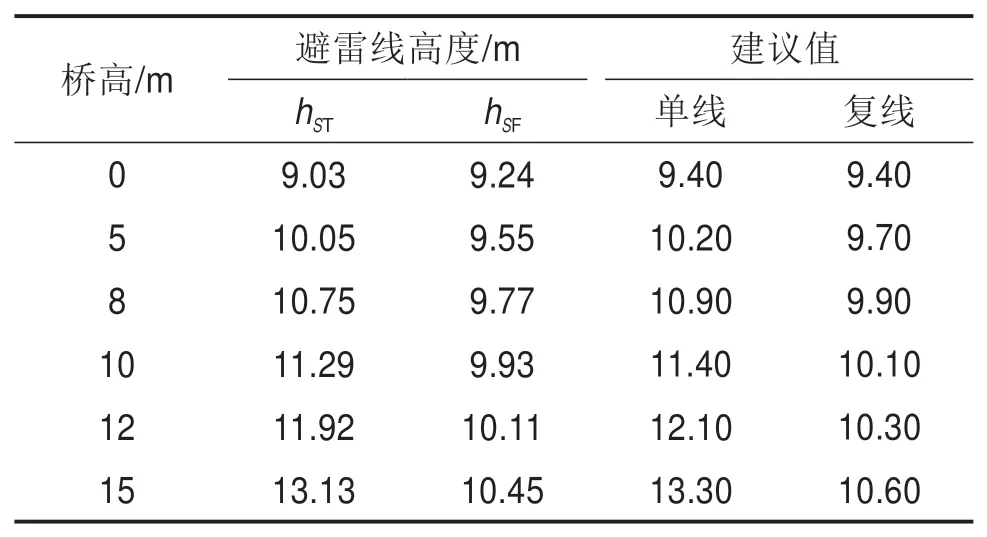
表3 接触网架设避雷线高度(滚球法)Table 3 Height of lightning protection wire for catenary(rolling ball method)

表1 ～表3中，高速铁路高架桥桥高为0时，基于电气几何模型的避雷线架设的计算高度为9.25 m，滚球法计算结果为9.24 m。两者结果相差不大，且滚球法的结果与文献[17]中的计算结果一致，说明章节2计算方法的正确性，也证明了电气几何模型同样适用于避雷线高度计算。

4 避雷线架设高度与高架桥高度的关系

4.1 避雷线高度与高架桥高度

将2种计算方法的结果绘制在图6中，发现采用电气几何模型计算的结果误差更大，滚球法计算的避雷线高度更为精准。从上述计算方法来看，电气几何模型需要考虑各导线之间的位置关系，情况更为复杂；而滚球法只需要考虑滚球半径，计算方法上更为简捷。整体来看，无论是基于电气几何模型还是滚球法，单线线路下计算的避雷线架设高度总是高于复线线路。是由于单线线路的避雷线架设高度计算既要考虑保护到馈线F，又要考虑到接触线T；而复线线路只计算保护馈线F时避雷线的高度。

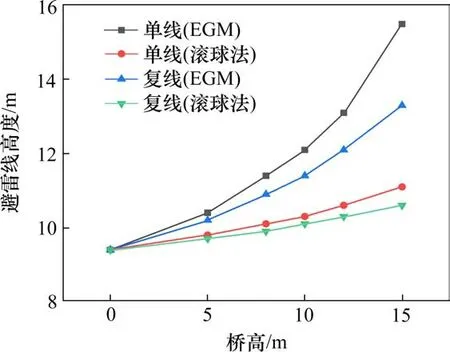
图6 避雷线架设高度与桥高的关系Fig.6 Relationship between the erection height of lightning wire and bridge height

2种方法计算的避雷线高度均随高架桥高度的增高而增大，由于滚球法的结果更为精确，下面重点分析滚球法的计算结果。从表3中可以看出，单线线路高架桥高度为0时，根据馈线F算出的避雷线高度较大，此时重点防护馈线；高架桥高度增加后，保护接触线T线的避雷线较高，防护重点应转移至接触线。复线线路只需要依据馈线F设计。

我国高速铁路大量采用了高架桥敷设，高架桥使得接触网对地高度增加，直击雷引雷宽度变大。电力部门根据模拟实验和运行经验对直击雷范围进行划分，认为一般高度的线路等值受直击雷面的宽度为4H+M(H为避雷线的平均高度，M为两避雷线之间的距离)。由于高架桥的增高使得引雷宽度增大，相应的避雷线的高度也随之增高。依据滚球法的计算，图中2种线路设计避雷线的高度随高架桥高度近似成线性增长，符合上述的过程分析。

4.2 避雷线高度与滚球半径

选择高架桥的高度为10 m，选用不同的滚球半径，对避雷线的设计高度进行计算，绘制图7。图中可以看出馈线F和接触线T均受到滚球半径的影响，滚球半径越大，计算的避雷线高度越小，且T线受到滚球半径的影响更大。选择合适的滚球半径对设计避雷线高度也十分重要。

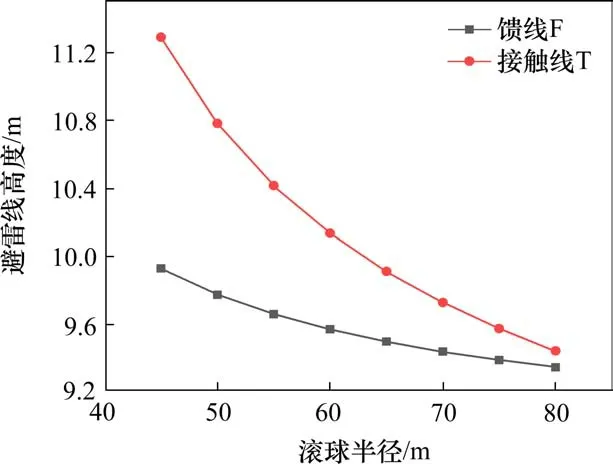
图7 避雷线高度与滚球半径Fig.7 Lightning wire height and rolling ball radius

5 实例分析

自从京广、京沪、广深港等南方地区高铁开通以来，深受雷击影响，暴露了防雷方面存在的缺陷，如接触网未设置架空避雷线，某些重点处所未设置避雷器等。以京广高铁为例，全线多数路段采用高架桥敷设，桥梁对地高度在8～16 m甚至更高。京广高铁直线段中间柱单腕臂结构参数：承力索对桥面垂直距离为6.9 m，AF线对桥面距离为8.5 m，两线路中心距离为5.0 m，侧面界限距离即接触线到支柱的水平距离为3.0 m，馈线到支柱的水平距离为1 m。桥高离地面距离选为10 m，代入公式(13)得避雷线的高度为9.93 m，实际工程中避雷线高度按10 m。改进措施的实施情况[18]：2013年6月完成了京广高铁广州北站—广州南站区间上下行增设架空避雷线改造，支柱高度按9.5 m计，避雷线在支柱顶0.5 m架设，具体杆号为下行：165号(广州北站)-1557号，上行：170号(广州北站)-1556号，计72.26 km。

从2013年6月完成试点改造并实施后，到2014年6月底的整年运行实际数据对比看，防雷效果改善显著，雷击跳闸明显减少。如表4所示2013年6月完成京广高铁广州北—广州南2个供电臂区间增设架空避雷线后，此后一年只发生8件雷击跳闸，比此前2013年上半年改造前半年平均跳闸13件减少9件。

表4 架设避雷线前后效果对比Table 4 Comparison of effects before and after erection of lightning protection wire

6 结论

1)基于电气几何模型和滚球法的原理，提出了高架桥区段接触网避雷线架设高度的计算方法，并详细推导了单线及复线铁路的避雷线高度计算公式，计算过程简捷，可为工程应用提供帮助。

2)经比较2种计算方法，电气几何模型和滚球法均适用于高架桥区段接触网避雷线的高度计算，但是滚球法的计算结果更精准，过程更简单。电气几何模型在导线的位置关系分析上具有更大的优越性，接触网的结构复杂导致计算结果误差较大。

3)单线铁路计算下的避雷线架设高度大于复线铁路，计算方法表明单线情况需要保护馈线F和接触线T，而复线只需要考虑馈线F。随高速铁路高架桥的增高，计算的避雷线架设高度也增加，近似成线性增长。

4)采用滚球法时，避雷线的高度与滚球半径密切相关。滚球半径增大，计算的避雷线高度相应降低。根据不同地区的雷暴活动，高架桥区段避雷线高度设计选择合适的滚球半径至关重要。