频率域2.5维广域电磁法正反演研究

周峰，张志勇，汤井田，李勇

(1.东华理工大学放射性地质与勘探技术国防重点学科实验室，江西南昌，330013；2.中南大学有色金属成矿预测与地质环境监测教育部重点实验室，湖南长沙，410083；3.中国地质科学院地球物理地球化学勘查研究所自然资源部地球物理电磁法探测技术重点实验室，河北廊坊，065000)

广域电磁法(WFEM)是一种人工源频率域电磁勘探方法，通过单分量测量并用其来定义具有全区特性的视电阻率，其特点是采用较小的收发距来获取较大的勘探深度[1−2]。该方法与可控源音频大地电磁法(CSAMT)[3]相比，摒弃了CSAMT 法在远区测量的限制、扩大了频率域有源电磁法观测区范围。目前，该方法已经被广泛应用于页岩气勘察、矿产勘探、地热以及水文、工程勘查等领域[4−5]。

当前，广域电磁法数据处理与解释仍然以一维模型为主，而实际的野外地电条件和观测形式通常不能视为一维，从而影响该方法资料解译的准确性。为此，人们针对2.5维问题有源电磁法开展了大量的研究工作。正演方面，为了处理场源奇异性，LEE 等[6−8]开展了基于二次场算法有源电磁法正演模拟研究，提高了2.5维有源电磁问题正演求解精度，但存在不能处理带地形复杂地电模型的不足。伪狄拉克函数的引入，成功解决了带地形的2.5 维可控源正演计算问题[9]；另外，海洋可控源电磁法2.5维正演计算中出现了一种差分算法，有助于场源奇异性问题的解决[10]。总体上，场源奇异性是制约2.5维可控源电磁法正演求解精度的关键因素之一，该因素同样会影响2.5维广域电磁法正演计算。反演方面，UNSWORTH 等[11]提出一种子空间反演算法并成功应用2.5维可控源电磁数据反演，该算法能够有效提高线性方程组的求解效率。另外，灵敏度矩阵的快速求解也是反演问题的关键，基于快速松弛算法的灵敏度矩阵快速近似求解策略被成功应用于2.5维可控源电磁法反演，有效提高了反演的效率[12]，该反演算法成功应用于实际数据的处理，取得了明显的效果；此后，底青云[13]采用类似的灵敏度矩阵计算开展了复杂介质2.5 维的CSAMT 反演研究。为了进一步提高该问题反演准确性和稳定性，雷达[14]结合OCCAM 反演算法实现了起伏地形条件下的2.5 维问题CSAMT 反演研究，分析了起伏地形的影响；另外，戴世坤等[15]提出了基于场分量的可控源电磁法2.5维问题共轭梯度反演算法。综上所述，虽已存在可控源电磁法2.5维正演与反演方面的研究成果，但基于场分量来定义广域视电阻率并以此为视参数来进行反演研究较少，因此，开展广域电磁法2.5维反演研究对提高其资料解释精度及推动该方法发展具有重要的研究意义。

本文作者首先从总场算法出发，推导2.5维广域电磁法满足的微分方程；然后，采用伪Delta 函数来降低源带来的奇异性，开展起伏地形频率域广域电磁法2.5 维正演模拟研究。在正演的基础上，构建广域视电阻率的正则化反演目标函数，采用非线性共轭梯度算法实现反演目标函数最优化求解，以有效避免显示、存储灵敏度矩阵，提高反演的求解效率。最后，设计层状介质模型验证本文开发的2.5维算法的正确性；并以正演为基础，分析广域视电阻率和Cagniard视电阻率的静态效应影响问题；然后，开展带地形与不带地形的低阻异常体以及组合异常体的地电模型的反演。

1 广域电磁法2.5维问题

1.1 基本理论

时间因子为eiωt，在准静态条件下，频率域有源的Maxwell电磁满足方程[16]为：

式中：E为电场强度；Η为磁场强度；Ms为外部磁流源；Js为外部电流源；=iωu，为阻抗率；ω为角频率；u为磁导率；=σ-iωε，为导纳率；σ为介质的电导率；ε为介质的介电常数。

假设地质体走向为y方向，对2.5维问题来说，对构造方向y方向进行一维傅里叶变换[17]，变换公式为

式中：ky为波数；F(x,y,z,ω) 为空间域场；(x,ky,z,ω)为通过构造方向y方向进行一维傅里叶变换得到的波数域场值。F(x,y,z,ω)可以表示为电场或磁场，通过式(3)，式(1)和式(2)可简化为：

化简式(7)和式(9)，可得：

将式(10)和式(11)代入式(12)和式(13)，可得：

将式(12)和式(13)代入式(10)和式(11)，可化简为：

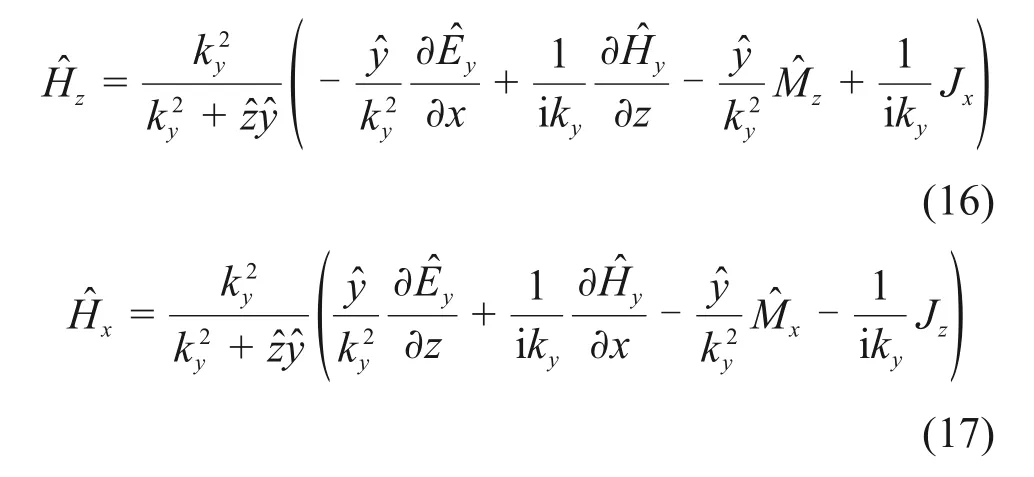
然后，将式(16)和式(17)代入式(5)，可得

同理，可得

式中：k2e=k2y+。式(18)和式(19)为频率域2.5维问题满足的耦合方程。

1.2 有限元矩阵合成

本文采用前期开发的收缩二叉树网格剖分技术[18−19]对求解区域进行离散，采用Galerkin 加权余量法将式(18)和式(19)满足的微分方程推导为有限元方程，具体公式为

运用Galerkin加权余量法对式(20)处理，得

式中：Nei为第i单元De上的插值函数；N为单元总数。将式(20)代入式(21)，可得同理，式(19)可简化为

式(22)和式(23)分别为沿走向电场分量和磁场分量满足的有限元方程，上述方程通过单元分析和刚度矩阵的合成得到一组稀疏复线性方程组：

式中：SE和SH分别为电流和磁流密度的场源积分值，分别为式(24)和式(25)的右端项；KE和KH为电场得到的刚度矩阵；KECH和KHCE均为电场Hy得到的刚度矩阵。通过分析可知，KECH=-KHCE，为了利用矩阵的对称性，则将式(24)和式(25)组合成为

式(26)右端源项利用伪Delta 函数进行场源加载，最后采用PARDISO 直接求解器[20]进行方程组求解，最后获取需要的波数域的电磁场各场分量值。

1.3 源项处理

对于有源场的计算，当采用总场算法时场源点是一个畸变点，在场源点附近电磁场变化很大，在有限的结点数量条件下通过线性、二次插值很难正确表示场源区附近的场值的变化。MITSUHATA[9]将pseudo-deta 函数引入电磁计算问题：

式中：τ为伪狄拉克函数的步长。

在二维条件下，三维场源在走向方向采用狄拉克函数，其他2个方向采用伪狄拉克函数，则场源可以表示为

除此之外，波束的选择在2.5维正演计算中是关键问题之一，需要效定波束的取值区间与波束的数量。在最有效的区间内，取合适的波束数量，可以在保证计算精度的条件下最大程地度提高计算效率。波束的选择与网格剖分相关，对式(18)，假设在均匀半空间条件下，只考虑走向y方向存在电流源且则有

MITSUHATA[9]在其采用四边形网格二次插值的CSEM 2.5 维正演计算中认为ky<1/Δ的有限元计算结果是满足精度要求。在经过大量试算后，在区间(1.0/xmax,1/Δ)中对数等距选择ky，其中xmax为计算模型横向最大尺度。

在此基础之上，为了得到获取广域视电阻率，采用迭代公式进行求解。

1)选取广域视电阻率初值ρ(0)，一般可取对应分量的波区视电阻率。

2)将ρ(0)代入视电阻率迭代计算公式(31)，求得第一次迭代后的视电阻率ρ(1)。

3)终止条件判断。若(ρ(1)-ρ(0))/ρ(0)≤η或者达到最大迭代次数(式中η为给定计算精度)成立，则停止迭代，否则ρ(0)=ρ(1)，令返回步骤2)，直到判断条件成立为止。

均匀半空间x方向水平电偶极子Ex分量表达式为

式中：FE-Ex(ikr)=1-3 sin2φ+e-ikr(1+ikr)。测量收发距观测点与偶极距正向的夹角φ，同时，记录供电电流I和供电偶极的长度。

2 正则化反演基本理论

反演是电磁法资料解释的关键环节，而正则化因子的选择与目标函数的优化又是正则化反演的2个重要过程[21]，本文研究采用“L-curve”曲线方法[22]，实现了正则化因子求解；另外，采用非线性共轭梯度算法实现平滑约束稳定因子的反演目标函数求解，提高反演过程的稳定性与计算效率。

采用正则化最小化目标函数：

式中：m为模型参数；dobs为观测数据；μ为正则化因子；φd(m,dobs)为数据拟合函数；为数据权重；G为正演算子；φm(m)为模型约束函数；Wm为模型权重矩阵；mapr为先验模型函数；φ(m,dobs)为反演目标函数。

反问题就是对目标函数求极值。本文采用非线性共轭梯度法利用迭代过程来实现目标函数极值点求取。需要对目标函数(32)求一阶梯度，其表达式为

将式(32)扩展为

1)令i=1，选择初始模型mi，同时求解目标函数的梯度gi=-∇φ(mi,dobs)。

2)令ui=M-1i gi.

3)选择1个αi，使得φm(m+αi gi)极小。

4)选择下一次更新模型mi+1=mi+αi gi以及目标函数的梯度gi+1=-∇φm(mi+1,dobs)。

5)当|gi+1|的值做够小或者达到设定的参数，即停止执行；否则执行步骤6)。

6)令βi+1=

7)令ui+1=M-1i+1gi+1+βi+1ui，同时，令i=i+1后返回步骤3)。

从以上计算过程可以知道，非线性共轭梯度算法只需要计算目标函数以及其梯度，不需要过多的矩阵的分解等运算，只需几个存储有限向量，因此，该算法适用于大规模问题的求解。

3 广域电磁2.5维正演算例分析

3.1 算法验证

为了验证2.5维广域电磁法程序的正确性，设计了如图1所示的地电模型，具体参数描述为：2层地电模型电阻率分别为100 Ω·m 与10 Ω·m，第一层厚度为512 m，在坐标原点(0，0，0)m处设置1 个沿y轴正方向激发源，源的长度为1 km，沿着x方向设置3个观测点，观测点的坐标分别为Site-A(1 020，0，0) m，Site-B(2 020，0，0) m，Site-C(5 020，0，0)m。分别计算3 个观测点的Cagniard电阻率及Ey，Hx和Hz这3 个分量广域视电阻率，计算结果分别如图2～4所示。从图2～4可知：2.5D视电阻率曲线与1D 结果曲线形态吻合[24]，Site-A曲线中的大部分频点位于近区与过渡带，而Cagniard视电阻率曲线在低频呈现连续上升；广域视电阻率曲线呈现出D 型曲线特征，与实际模型吻合。Site-B广域视电阻率表现出明显的D型曲线特征，Cagniard 视电阻率在4 Hz 左右出现过渡带低阻；Site-C 总体表现出远区曲线特征。观测点Site-A和Site-B的Hx分量的视电阻率曲线在低频差别较大，原因是Hx分量在近区与过渡区含有的地下介质电阻率信息少，在求取广域视电阻率过程中，求解非线性方程小的误差将引起较大的视电阻率差异。以上结果分析表明，本文开发的2.5维正演程序正确且有效。

图1 2层介质模型Fig.1 Two layer media model

图2 Site-A观测点2.5D与1D计算结果对比Fig.2 Comparison of 2.5D and 1D calculation results at observation point Site-A

图3 Site-B 观测点2.5D与D计算结果对比Fig.3 Comparison of 2.5D and 1D calculation results at observation point Site-B

图4 Site-C 观测点2.5D与1D计算结果Fig.4 Comparison of 2.5D and 1D calculation results at observation point Site-C

3.2 静态效应分析

为了模拟地表不均匀体对广域视电阻率的影响，设计如图5所示的地电模型，其中在均匀大地的电阻率为100 Ω·m 中放置了6 个矩形块状异常体，其中4个上顶埋深为16 m，电阻率从左到右分别为10，1 000，10 和1 000 Ω·m；此外，在地下存在2个规模较大的块状异常体，块状异常体的顶部距离地表埋深为128 m，电导率为10 Ω·m。分别计算x与y方向的电性场源激励下的Cagniard 电阻率及电场分量定义的广域视电阻率响应，计算结果如图6所示。

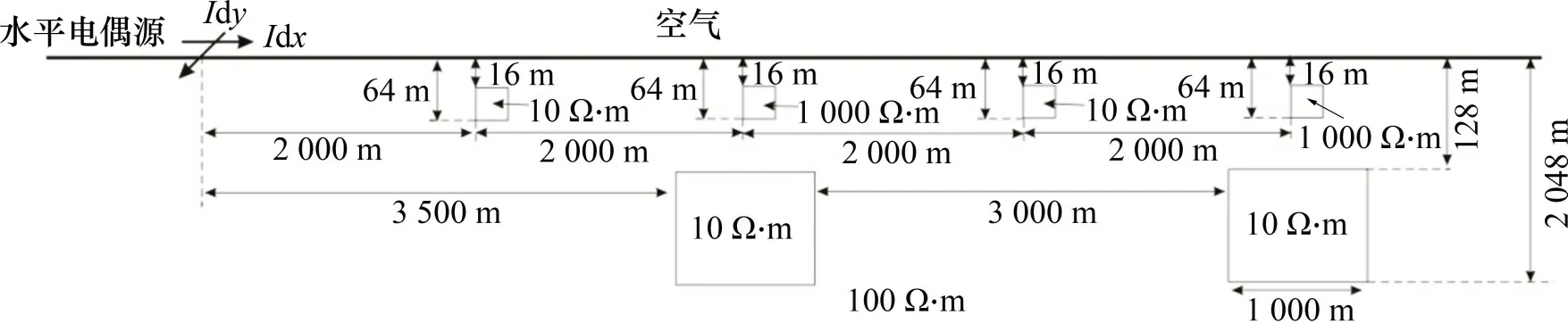
图5 静态效应地电模型Fig.5 Geoelectric model of static effect

图6 静态效应地电模型计算结果Fig.6 Calculation results of static effect geoelectric model

由图6可知：在垂直走向方向Idx场源激励下，浅部异常体呈现出条带状，对视电阻率剖面影响较大；而沿走向方向Idy场源激励下，浅部异常体产生的静态效应比垂直走向方向激励源产生的静态效应小，在沿走向方向场源激励下，浅部异常体呈现出局部圈闭的异常现象；在与背景电导率存在10 倍差异的条件下，低阻的异常现象比高阻的明显；浅部异常体产生的静态效应对Cagniard电阻率影响远比单分量定义的广域电阻率的影响大，尤其是当场源方向垂直走向方向时，较深的异常体严重畸变。

3.3 广域电磁法地形影响

地形能够使电磁法数据产生严重畸变。为了进一步分析广域电磁法和传统可控源电磁法在视参数定义受地形影响程度，设计均匀半空间存在地形的模型进行试算研究，模型参数如图7所示，在均匀大地(100 Ω·m)上存在1 个截面为梯形的地表地形，分别计算2个方向场源激励下Cagniard电阻及电场分量定义广域视电阻率地形响应，计算结果分别如图8和图9所示。

图7 地形模型Fig.7 Terrain model

图8 x方向场源的计算结果Fig.8 Calculation results of x direction horizental electric dipole source

由图8和图9可见：地形对x方向场源的激励明显比对y方向场源的激励大，且对Cagniard电阻的影响比对广域电阻率的影响大，近区与过渡带数据畸变大。

图9 y方向场源的计算计算结果Fig.9 Calculation results of y direction horizental electric dipole source

3.4 广域电磁2.5维反演算例

3.4.1 单个异常体反演算例

建立如图10所示模型，分别开展不带地形、带地形(图10中虚线)条件下存在单个异常体的反演。将正演计算视电阻率加入1%随机噪声作为反演输入数据。

图10 单个异常体反演模型示意图Fig.10 Schematic diagram of a single anomaly body inversion model

图11所示为单个异常体x方向电偶源的Ex分量定义广域视电阻率经12 次反演迭代得到的计算结果。由图11可知：带地形与不带地形条件下均能够给出异常体大致位置，异常体的边界平滑过渡，反演结果准确。图12所示为采用Cagniard 视电阻率作为反演数据得到的反演结果，同样显示了较高的准确度。以上结果表明，无论是广域视电阻率的反演还是Cagniard电阻率的反演，深部电阻率的收敛都较慢，低阻体向深部且偏向场源方向延伸。

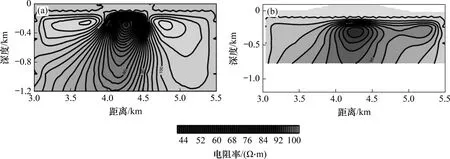
图11 单个异常体x方向电偶源Ex分量定义广域视电阻率反演结果Fig.11 Inversion results of Ex component of wide field apparent resistivity for single anomaly body in x-directional horizontal electric dipole source

图12 单个异常体x方向电偶源Cagniard分量定义视电阻率反演结果Fig.12 Inversion results of Cagniard apparent resistivity for single anomaly body in x-directional horizontal electric dipole source

3.4.2 组合异常体反演算例

建立如图13所示模型，分别开展不带地形、带地形(图13中虚线)条件下存2 个异常体的反演。将反演数据加入1%随机噪声以正演计算视电阻率。平滑模型约束下，应用非线性共轭梯度求解的反演结果如图14所示。组合异常体反演结果表明，x方向电偶源Ex分量定义广域视电阻率反演得到的低阻异常体拟合程度明显比高阻的高，高阻反演得到的电阻率差异明显。同样地，无论是广域视电阻率反演还是Cagniard电阻率反演，深部电阻率的收敛速率都较慢，表现为低阻体向深部且偏向场源方向延伸。

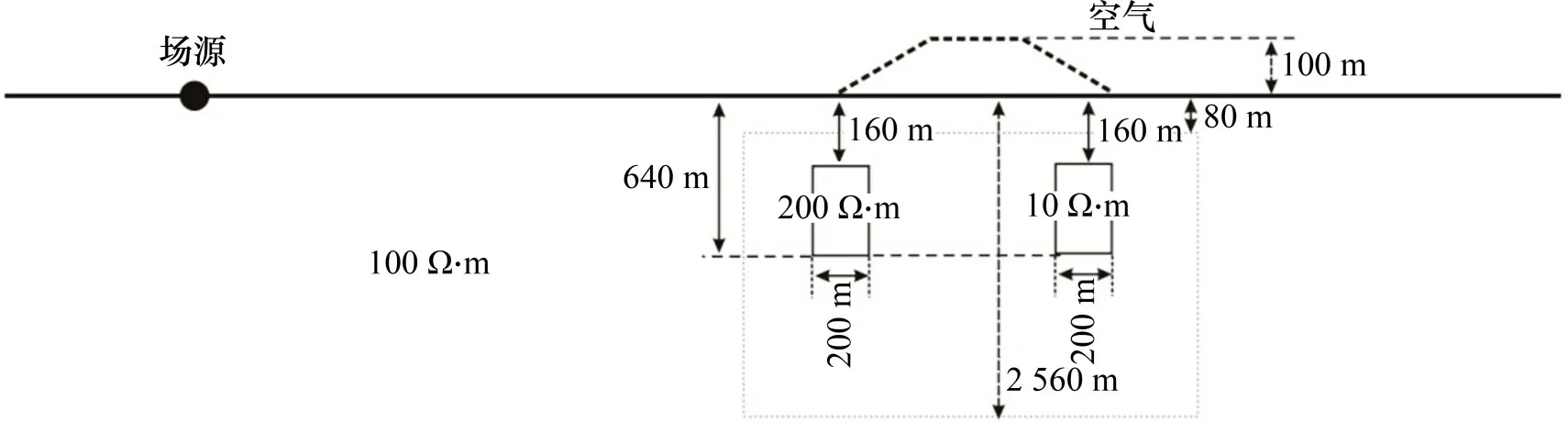
图13 组合异常体反演模型示意图Fig.13 Schematic diagram of a combination anomaly body inversion model

图14 2个异常体x方向电偶源Ex分量广域视电阻率反演结果Fig.14 Inversion results of Ex component of wide field apparent resistivity for combination anomaly body in x-directional horizontal electric dipole source

4 结论

1)在二维地电条件下，浅部异常体引起广域电磁的静态效应。总体而言，Ex形式定义的广域电阻率受静态效应影响比Cagniard 电阻率的影响小，且赤道装置得到的广域视电阻率受静态效应的影响比轴向装置得到的广域视电阻率所受的影响小。另外，地形对x方向场源激励明显比y方向场源激励大，且对Cagniard电阻影响比广域电阻率的影响大，近区与过渡带数据畸变大。

2)本文开发的广域电磁法2.5维反演结果能够很好地反映异常所在的位置，反演结果总体准确，不足之处在于底部边界收敛速率较慢。

3)为了进一步测试本文算法的可靠性，下一步将开展实际数据测试，以便对本文开发的算法提出相应的改进措施，完善算法。