不确定需求下生鲜农产品物流配送路径优化研究
2021-10-18李钰峰郭盼雨
李钰峰 李 攀 郭盼雨
(山东理工大学管理学院,山东 淄博 255012)
1 概述
为了及时满足消费者的需求,冷链物流逐渐向多批次、小批次的发展方向转变以满足消费者的不同需求,但是我国的冷链配送生鲜农产品相应体系构建并不完善,这就造成某些生鲜农产品减少了其经济价值和营养价值,企业的利润也会受到很大的影响,在保证其质量等方面满足消费者,这就使得企业在生鲜农产品配送过程有着更加严格的要求。为了能够将产品更加高效快速的送到消费者手中,选择更加合理的配送路径就变得尤为重要。
生鲜农产品的配送问题一直是学者们对物流进行研究时的重点问题。崔岩(2017)等在对生鲜农产品的路径优化进行研究时,对不确定需求下的生鲜电商进行路径优化问题,建立生鲜电商的路径优化模型,用累积前景理论对问题进行分析,并用改进粒子群算法对模型进行求解[1]。陈久梅(2018)等在对生鲜农产品的物流配送路径研究时,针对消费者的不确定需求,采用多隔室车辆配送方法,以配送成本最小为目标,运用粒子群算法对建立的路径优化模型求解,在解决问题的基础上发现该算法的收敛性良好[2]。
将不确定需求下生鲜农产品物流配送路径优化问题的总成本进行思考,结合生鲜农产品物流配送的特征,将配送过程中产生的运输、货损等成本进行思考,同时考虑在实际的配送过程中客户可能会存在需求不确定的情况,当不能满足客户要求时会产生缺货成本。在满足客户时间要求的情况下,以总成本最小为目标,对配送路径进行合理优化,对生鲜农产品物流的发展起到一定的促进作用。
2 不确定需求下生鲜农产品物流配送路径优化研究
2.1 问题描述
本研究是以一个企业的配送中心为多个客户提供物流配送服务为前提进行建模,将客户需求量等作为研究要素,以配送总成本最小为目标进行如下假设:
(1)配送车辆型号相同,载重相同。
(2)运输车辆在完成配送服务后要返回配送中心。
(3)客户位置已知,配送时间已知。
(4)每个客户只能有一辆车一次性完成配送。
(5)不存在中途再指派车辆的情况
(6)允许配送车辆和配送中心产生缺货的情况,但产生缺货成本。
(7)客户需求量未知但服从一定的随机分布。
2.2 配送成本分析
2.2.1 车辆固定成本
车辆的固定成本是指配送车辆在提供服务过程中所产生的费用,一般包括在运输过程中所产生的损耗、司机的报酬等,该成本一般为常数,不受车辆所载货物重量的影响。固定成本表示为:

式中,C1为运输车辆总固定成本;fk为每辆车的固定成本;K 为配送车辆的数量,k 表示车辆序号(1…k)。
2.2.2 运输成本
车辆对客户进行服务时所产生的各种费用被称为车辆的运输成本。通常包括车辆的燃油费、维修费等。一般情况下车辆的运输成本与运输距离成正相关,距离越远,车辆的运输成本越高。所以运输成本用公式表示为:

上式中,C2表示为车辆总的运输成本α 为单位距离的运输成本;dij表示客户点i 到客户点j 的路程;xij为相应的决策变量,当第k 辆车从客户点i 到客户点j 时,xij=1,反之为0。
2.2.3 货损成本
本文的主要研究对象生鲜农产品,企业在配送过程中,货物会因为不同的因素而受到损坏。因为本为研究路径优化,故只考虑在配送过程中的货损情况。因为运输车辆为冷藏车,所以货物在运输过程中处在一个比较稳定的环境中,所以货损程度与服务时间长短有关。本文货损成本是指车辆服务时间的积累引起的货物损失。货物的腐败速率我们认为是指数型的变化。货损函数公式表示为:Qt=e-βt,Qt表示生鲜农产品的质量,β表示生鲜农产品对时间敏感系数Qt与生鲜农产品对时间敏感系数和配送时间有关。配送过程中货损成本为:

2.2.4 能耗成本
为了使生鲜农产品保持新鲜,在运输过程中必须消耗许多能源来维持,以至于在到达客户点这个过程中产品处于低温环境,这个过程会产生一部分的制冷成本,而且在对客户进行服务时,冷藏车内部气体会与外界进行热交换,导致车厢内部温度升高,为了维持相对稳定的冷藏环境,需要消耗更多的能源来维持车厢内部得低温环境,假设运输过程中能耗成本与客户数量和配送时间有关,则能耗成本为:
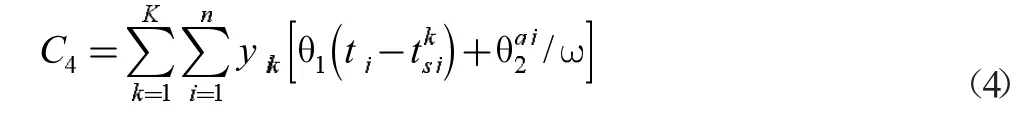
式中C4表示总的能耗成本;θ1表示配送过程中单位时间内生鲜农产品能耗;θ2表示在卸货过程中单位时间内生鲜农产品能耗;tj表示车辆到达客户j 的时间;tksj表示第k 辆车到达客户j 的时间;ω 对客户进行服务时装卸效率。
2.2.5 惩罚成本
生鲜农产品因为具有易腐烂的特点,所以客户会对生鲜农产品送货时间进行一定的约束,若配送车辆没有在顾客要求时间段内送达,则会产生一定的惩罚成本,通常情况下对配送时间的要求一般采取软时间窗,产生的惩罚成本表示为:

式中C5表示i 点的惩罚成本;M是一个无穷大数;λ2提前到达后的惩罚系数;λ3延时到达后的惩罚系数;ti产品到达i 客户点的时间;eti表示客户可以接受的最早服务时间lti表示客户可接受的最晚到达时间;[ETi,LTi] 表示客户可接受最佳服务时间。如果在最佳服务时间段内对客户进行服务,则惩罚成本为0,如果是在可接受范围内而不是在最佳服务时间段对客户进行服务,则会产生一定的惩罚成本。
2.2.6 缺货成本
由于物流行业的不断发展,客户需求量会随着季节、个人口味、产品质量等因素的影响而产生变化,现在大多数路径优化问题中,为了建立模型和求解都变得更加简单,客户需求量一般都是确定的数值,但在现实的配送过程中,客户会因为一些因素导致对生鲜农产品需求量变得不确定。在这种情况下,客户的不确定需求会影响总成本以及配送路径的规划,在本文中,把客户需求量作为随机变量,但会服从一定的随机分布。
在配送路径优化过程中,如果配送车辆在某个客户点没有满足客户需求,就会在配送过程中产生缺货成本,表示为:

式中C6表示总的缺货成本;γ 表示单位生鲜农产品的缺货成本;dk表示车辆k 对客户进行服务时客户的实际需求量;wk表示车辆k 的实际运输量。
2.3 模型建立
对于不确定需求下生鲜农产品物流配送路径优化问题,将配送过程中总成本最小作为主要目标,建立如下路径优化模型:
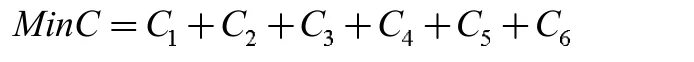
3 算法设计
路径优化问题很明显是一个NP-hard 问题,因此在解决问题过程中要理论与实践相结合。蚁群算法是一种受到自然界中蚁群觅食的启发而产生的一种算法,因其具有好的鲁棒性以及搜索最满意解的能力,所以本文选择用蚁群算法来对模型进行求解。
4 算例分析
4.1 算里描述
一个配送中心,该配送中心有多辆冷藏车,需要为20 个客户提供配送服务,将配送中心和客户点从0 到20 进行编号,其中配送中心编号为0,假设客户点需求服从正态分布,算例的基本数据如表1。
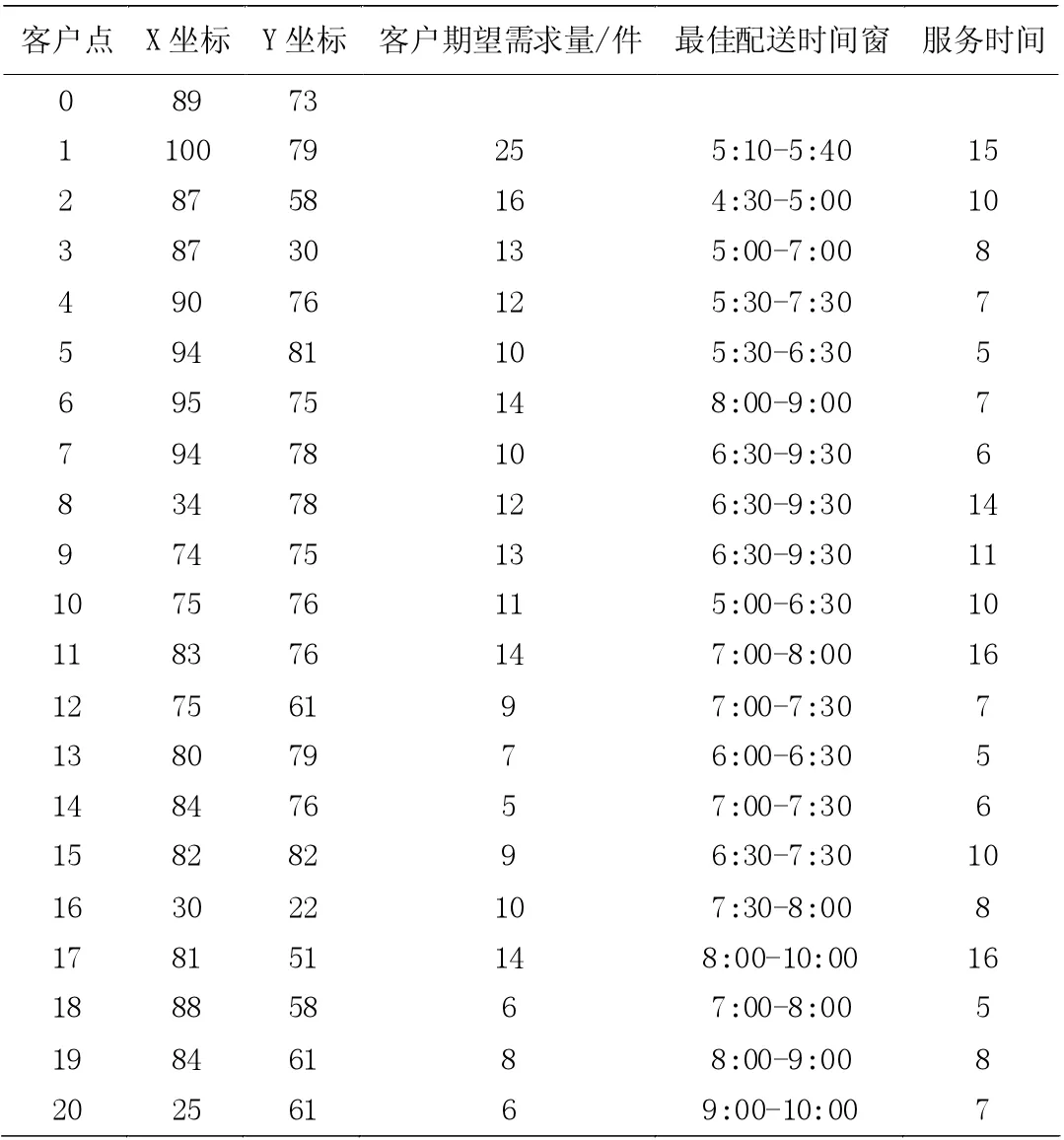
表1 客户点信息
车辆固定成本fk为300 元/辆;单位距离成本α 为2 元/千米;生鲜农产品对时间敏感系数β 为0.005%;生鲜农产品单价P 为30 元/件;配送过程中单位时间内生鲜农产品能耗θ1为1.2 元;卸货过程中单位时间内生鲜农产品能耗θ2为1.5元;为客户服务是的装卸效率ω 为2 件/分;运输过程中生鲜农产品常数λ1为0.8;提前到达客户点惩罚系数λ2为70/h;拖后到达客户点惩罚系数λ3为85/h;生鲜农产品缺货成本γ 为8 元/件。
4.2 运行结果
为了研究客户需求量的变化对配送路径优化产生的影响,首先把客户期望需求量作为客户实际需求量,把表1 中的客户期望需求量作为客户实际需求量来研究确定模型下的生鲜农产品物流配送路径优化;第二种是研究客户需求不确定情况下的生鲜农产品路径优化,假设当方差为1,2,3 时,客户需求量满足率为98%,而且服从X~N(μ,σ2)。首先客户需求量确定的情况下,对配送车辆进行路径优化并求取各项成本,然后在随机模型下对不同方差时的各项成本进行比较。
4.2.1 需求量确定情况下模型求解
将相关参数和初始数值导入到MatlabR2013a 软件中求解,经过50 随机测试后获取最优结果,最优状态下配送总成本为3478.9 元。
蚁群算法运算后得到的最优路径如图1 所示,我们可以看到在正常情况下配送中心需要6 辆车对客户点进行服务。
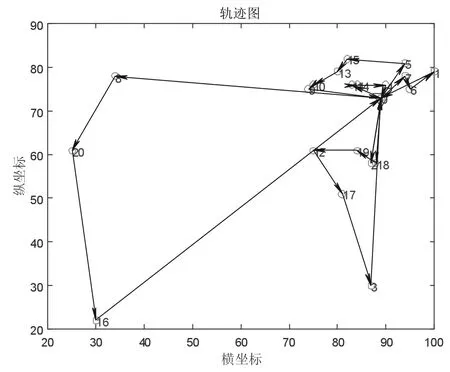
图1 配送路线图
根据软件计算我们得到相关配送的成本明细如表2 所示。其中虽然配送车辆2 车和6 车有惩罚成本,但都在客户可接受时间范围内完成了配送,而配送车辆1 车、3 车、4 车和5 车都在客户要求的最佳时间段内完成了配送,故惩罚成本为0。

表2 车辆配送成本
4.2.2 需求量不确定情况下模型求解
在需求量不确定情况下,设配送中心对各客户点满足率为90%,且客户点需求量服从正态分布X~N(μ,σ2),根据所学相关知识,当x=μ+z*σ 时,z 为1.29,得到各客户点在服从正态分布情况下需求量的变化,使用matlab 软件对以上数据进行物流配送路径优化,对在σ 不同的情况下进行随机测试50 次,如表3,取路径优化的最优结果并对配送成本进行分析。

表3 需求确定和不确定情况下成本汇总
通过表3 的数据我们可以看到,固定成本的高低只与配送车辆数量有关,需求确定情况下固定成本只需要1800 元,而在需求不确定情况下时,固定成本最高达到2400 元。运输成本、货损成本、能耗成本和惩罚成本在两种不同情况下差别不大,总成本存在一定差距的主要原因是因为缺货成本出现较大波动,而且随着方差越来越大,缺货成本变动加剧。
5 结论
相比较于常温配送,生鲜农产品对配送环境的要求更加苛刻,需要考虑更多的因素,各项配送成本也会随之增加,所以企业为了使成本降低需要对生鲜农产品物流配送进行合理的路径优化。在现实情况中面对客户点需求量不确定情况下,企业要提前做好调研防止因为缺货而对总成本产生影响。本文以配送总成本最小为目标,在需求量不确定情况下,运用蚁群算法进行求解,使得既能总成本最小又能满足客户需求。
