含对数的积分之求解方法研究

李庆娟

(大连财经学院 管理学院，辽宁 大连 116622)

在一元微积分中,含对数的积分是一类常见的积分求解问题,有些题目甚至较难,求解方法往往具有较强的灵活性和技巧性,一般地,我们要根据题目中被积函数的特点采用不同的求解方法和技巧,典型的计算方法可总结为换元法、分部积分法、累次积分法、特定结论法。

1 换元法

1.1 凑微分换元法

凑微分法是计算积分的主要方法之一,又称第一类换元法,主要是根据被积函数的特点进行相应的凑微分,进而换元求解,如果熟练的话,可省略中间的换元过程直接求出积分。

解 先观察被积函数特点,注意到分子lnx+1=(xlnx)′,将整个分子凑微分再求解,

解 此题不具备直接可凑微分的项,但可以利用添项法,将分子分母同乘以lnx,这时会有(xln2x)′=ln2x+2lnx,故将分子凑微分即可

=ln|xln2x|-ln|1+xln2x|+C。

1.2 第二类换元法

第二类换元法与凑微分换元法思路不同,前者是直接采用变元进行换元,后者是先凑分再进行换元,第二类换元法中常用的换元方法主要有直接代换法、根式代换法、倒代换法、三角代换法等,它是求解积分非常重要的方法。

1.2.1 直接换元法

解 令t=lnx,则x=et,dx=etdt

即将不定积分分成两个积分,选择第一项用分部积分法求解

1.2.2 根式代换法

=2tln(1+t2)-4t+4arctant+C

1.2.3 三角代换法

解 令x=tant,则dx=sec2tdt,

=-costln(tant)+ln|csct-cott|+C

1.2.4 倒代换法

1.2.5 灵活代换法

对于含有对数和三角函数的定积分求解时,可根据被积函数和积分区间所给形式灵活采用相应的代换形式。

2 分部积分法

解 根据选择标准选幂函数凑进去作为v

=xsin(lnx)-xcos(lnx)-I

3 累次积分法

所谓累次积分法就是根据所求的定积分的形式先将其先转化为一个二重积分,再通过改变积分次序求解对应的累次积分。

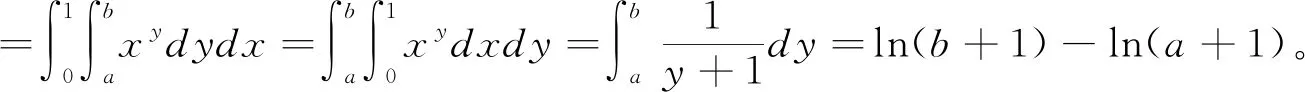
4 特定结论法

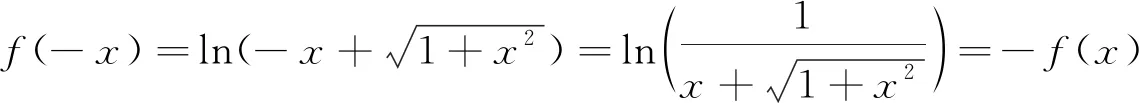
5 结束语

综上,我们通过实例分析给出了含对数积分的几种重要求解方法,一般地,被积函数形式不同采用的方法就有所不同,在学习积分的过程中,我们要善于思考、研究、总结和归纳,这样再遇到此类积分时,思路将更开阔,问题会轻松解决。