TDLAS气体检测系统仿真与影响因素分析

王国水， 郭 奥， 刘晓楠， 丰 雷， 常鹏浩， 张李明， 刘 龙， 杨晓涛*

1. 哈尔滨工程大学动力与能源工程学院， 黑龙江 哈尔滨 150000 2. 哈尔滨工程大学物理与光电工程学院， 黑龙江 哈尔滨 150000

引 言

船舶运输在我国运输行业中占据重要地位， 为我国的经济发展做出了巨大贡献[1]。 但与此同时， 船用内燃机排放物也带来了严重的环境问题， 其中尤以氮氧化物(NOX)污染较为严重， 但我国对于船舶大气污染物排放的评价、 管理以及限制标准、 政策还不够完善[2]。 开展对船舶污染物排放的量化研究和特征分析， 对于船用柴油机燃烧过程的优化研究、 减少废气排放、 切实提高环境空气质量、 保障公众健康以及对排放限制标准的制定都有着重要意义。

自可调谐激光器用于污染物检测开始[3]， TDLAS技术就在不断进步。 如今在调制信号产生、 信号检测、 降噪以提高信噪比等等各方面都进行了改进[4]， 并在增加检测气体的种类、 提高检测精度等方面有了长足的进步， 检测方式和可以检测的参数越来越多样化[5-6]， 并对于环境因素产生的影响提出了补偿方法[8]。 相比于传统测量方法， TDLAS技术具有抗干扰性好、 精确度高、 响应时间短、 能够实现实时动态测量等优点， 前景广阔。 而TDLAS的广泛应用也对其研究提出了更高的要求， 因此利用数学软件对检测过程进行模拟具有很重要的意义， 通过模拟对检测过程进行研究， 可以为其后的实际测量奠定基础。

对于目前实际存在的船舶排放问题， 赵嫦欣[9]以NO为目标气体， 利用二次谐波信号进行了浓度反演， 通过三段式温度划分进行配分函数拟合， 探究了温度、 压力对吸收系数和谱线峰值的影响， 用福依特线型不断计算温度、 压力以进行修正。 构建了气体浓度检测模型， 用二次谐波比一次谐波作为检测信号以消除激光器和放大器的影响， 对气体浓度进行了反演并计算误差。 采用4次多项式进行配分函数拟合。 除温度、 压力外， 还重点探究了波长调制法的波形设置参数、 调制系数等对信号的影响， 通过引入参考气室的方法消除温度、 压力波动为测试结果带来的误差， 直接得到待测参数， 不再进行不同环境条件下的浓度-信号幅值曲线拟合。

1 TDLAS检测系统基本原理

1.1 比尔-朗伯定律

当一定频率的激光照射气体时， 其与气体分子内部的电子、 原子核等相互作用， 气体分子吸收辐射的能量ΔE， 从低能级的基态跃迁到高能级的激发态， 从而产生吸收光谱。

假设入射光强I0, 穿透光强为It， 则根据比尔朗伯定律

It(ν)=I0(ν)exp[-S(T)Nφ(ν)cL]

(1)

式(1)中，S(T)[cm·mol-1]是气体吸收特征谱线的强度；L[cm]是有效光程长；φ(ν)[cm]是谱线的线型函数；N[mol·cm-3]为气体分子密度；c为气体的浓度， 用体积浓度表示。

1.2 波长调制光谱技术

由于直接吸收技术存在一些不足， 因此在直接吸收技术的基础上， 发展出了波长调制光谱技术(WMS)和频率调制技术(FMS)[7-8]。 波长调制技术的主要工作原理： 在低频扫描信号的基础上叠加高频调制信号对激光器的注入电流进行调谐， 激光器的输出频率可以表示为

(2)

I(ν)=I0[1+icos(ωmt)]exp[(-α(ν)cL]

(3)

式(3)中，I0和α(ν)分别为入射光强和气体吸收系数，i为强度调制系数。 对α(ν)进行傅里叶级数展开后， 得到

(4)

式(4)中，ν0为谱线中心频率， 则可得到Hn

(5)

若定义An=HnS(T)NcL， 则透射光强的二次谐波、 一次谐波可分别表示为式(6)和式(7)

(6)

(7)

式中，G为探测系统光电放大系数。 在中心频率处阶数n为奇数时An=0， 而A0和A2相对1很小， 可以将其忽略， 因此得到

(8)

从式(8)中可以看出，S2f/1f在一定环境条件下与浓度具有线性关系， 且与激光器光强和放大倍数无关。

2 TDLAS检测系统仿真及浓度反演

2.1 检测系统仿真

使用波长调制法进行浓度检测时， 激光器经过电流调谐后， 发出的激光传输到气室， 激光经过气室后被光电探测器接收， 光电探测器将光信号转化为电信号， 然后经过前置放大器放大滤波再经锁相放大器调解得到各阶谐波信号， 通过谐波信号可以将气体的参数信息反演出来。 TDLAS检测系统仿真主要由以下几个部分组成： 光源调制、 线型函数拟合、 模拟气体吸收、 线强函数S(T)拟合、 锁相放大器各部分。

本工作利用软件对波长调制的测量过程进行模拟。

首先对光源调制部分进行仿真， 对激光器进行调谐， 用来调谐的电流信号由低频锯齿波和高频正弦波叠加而成， 低频锯齿信号用以调制激光使其波长来回扫描选定的NO气体的吸收中心波数。 所选的中心波数为1 900.076 cm-1。 调制后的激光波数如图1所示。

图1 调制激光波数变化

对于吸收谱线， 采用洛伦兹线型函数来描述。 其所需数值都可以从HITRAN数库中查到。 经过调制的激光在透射过吸收气室后， 光强明显降低， 光电探测器接收后生成电信号， 经过气室吸收后的光强如图2所示。

图2 经气室吸收后的光强

光电探测器将接收到的信号输入锁相放大器， 由锁相放大器从中提取各次谐波。 研究中采用正交型锁相放大器， 采用两个频率相同， 相位相差π/2的正弦信号作为参考信号。 输入信号与参考信号分别相乘， 得到混频信号， 混频信号经过低通滤波， 得到谐波信号的X和Y分量[9]， 其中一倍频和二倍频的X和Y分量分别如图3(a,b)所示。

图3(a) 一倍频X和Y滤波分量

图3(b) 二倍频X和Y滤波分量

谐波信号R见式(9)

(9)

选择的浓度反演方案为峰值拟合法， 采用S2f/1f信号在中心频率处的峰值与浓度的关系来反演浓度， 仿真中得到的S2f/1f如图4所示。

图4 S2f/1f信号

对于线强函数S(T)的拟合， 其中的配分函数Q(T)用多项式拟合的方法得到近似值

Q(T)=a+bT+cT2+dT3+eT4

(10)

式(10)中， 系数a，b，c，d，e均值与待测气物质的参数有关。 由于在选定的中心频率附近有多个吸收， 所以吸收线强是多个效果的叠加， 从HITRAN数据库查询的数据如表1。

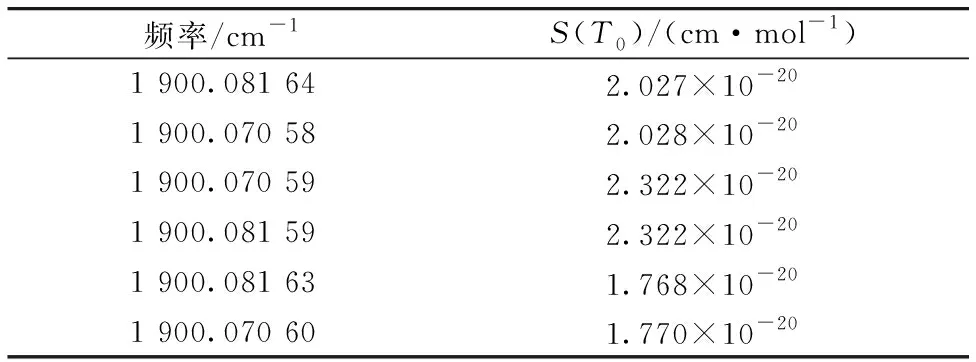
表1 选取的吸收线强数据

在1 900.076 cm-1的中心频率附近， 选取吸收较强频率的线强来计算总的线强。

2.2 气体浓度反演

最终从锁相放大器得到信号S2f/1f， 应用峰值点法， 在一定的温度、 压力条件下， 气体浓度与信号S2f/1f的峰值正相关。 在设定的条件下进行浓度的拟合： 设定温度为300 K， 压力为1 atm， 光程20 cm， 利用模型测定不同浓度下的信号峰值。 浓度与信号峰值关系如表2所示。

表2 不同浓度(体积分数)对应的信号峰值

设已知NO气体浓度为A， 对应浓度测定的峰值为B， 采用最小二乘法， 得到拟合公式：B=1.51×10-3A+0.016 95， 绘制散点图和拟合曲线， 如图5所示。

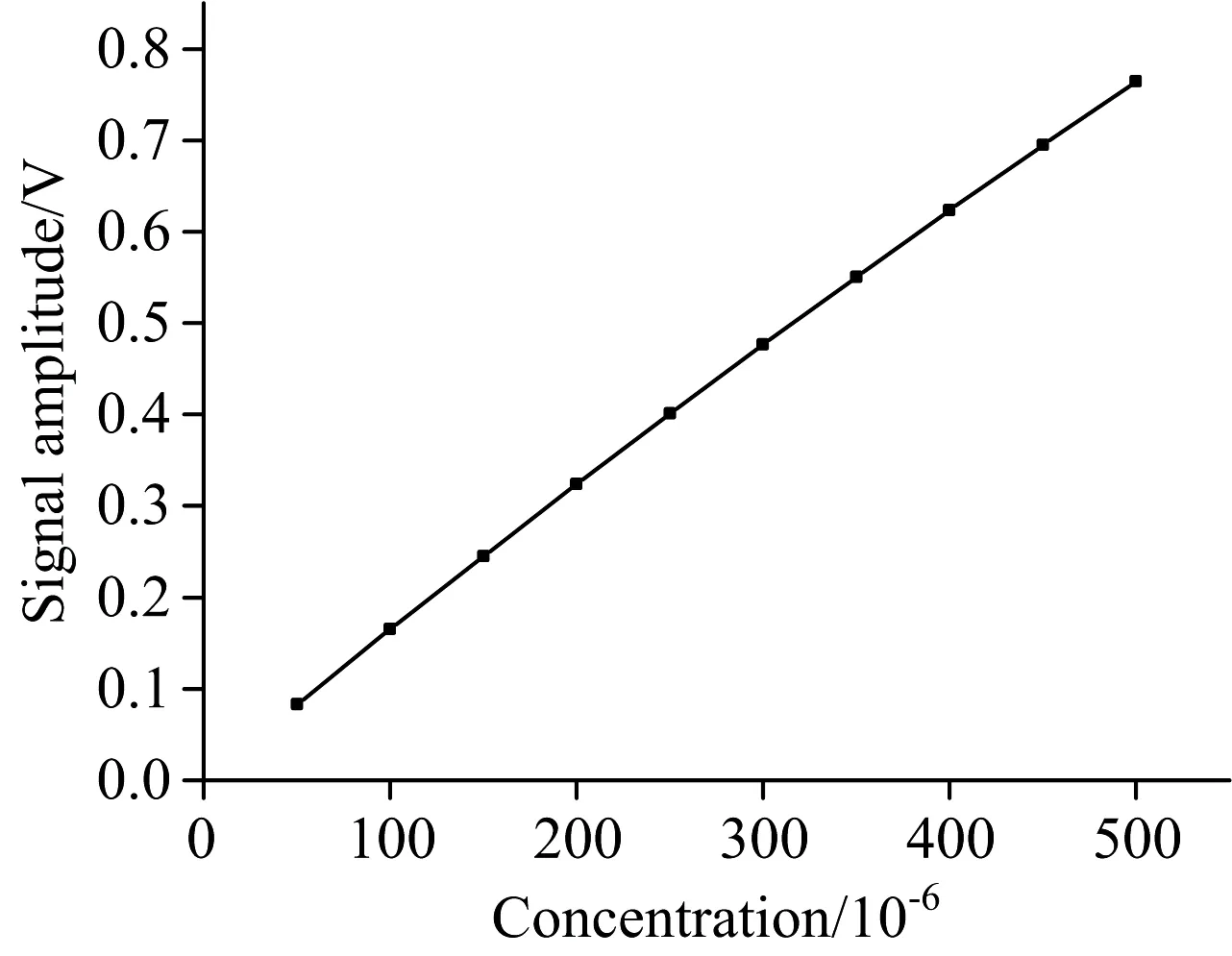
图5 浓度-信号峰值拟合曲线

可以利用拟合曲线来检测未知浓度， 一般采用插值法来检测未知浓度。 设定的气体浓度及反演结果如表3。

表3 反演气体浓度(体积分数)及误差

当设定的浓度比较低时， 拟合反演所得到的结果误差比较大， 说明依照这种方法不能检测过低的浓度。 而在几十到几百ppm的范围内， 反演的误差相对小一些， 说明在这个浓度范围是比较合适的拟合范围。 降低误差的方法主要有两种， 一是采用更多的标定点得到拟合曲线， 二是选取更多的信号峰值点并取平均值， 以得到更加贴切的拟合曲线。

3 参数对波形影响的分析

利用谐波信号来对气体进行检测， 信号幅值决定了结果的精确性。 而气体吸收谱线中的一些参数会随环境变化而变动， 因此谐波信号的幅值会受到环境因素影响。 需要分析环境因素对测量结果产生的影响并对其做出修正。

3.1 压力对谱线的影响

气体介质的压强是对谐波波形产生影响的因素之一， 气体线宽和分子密度会随着压强增大而增大， 同时， 只有在一定的温度、 压强、 调制系数的条件下，S2f/1f信号峰值与浓度成正比关系。 因此， 设定在温度300 K时， 改变气压值， 观察气压对波形的影响。 设定的气压值为0.6， 0.8， 1， 1.2和1.4 atm， 所得二次谐波波形如图6。

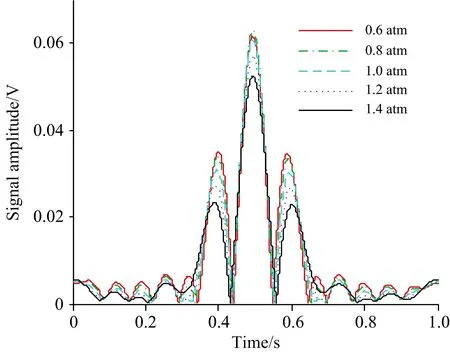
图6 不同气压下的二次谐波

从图6可以看出， 在设定的范围内谐波信号峰值随压强增加先增大而后减小。 若将An表示为式(11)

(11)

谐波信号与An成正比，An中的系数N/γL消除了压强的影响， 但是由于γL会随压强增大而增大， 从而导致Kn的值发生变化， 因此谐波信号会随之改变。

3.2 温度对谱线的影响

气体吸收谱线中的参数如线强、 线宽、 分子密度数等都与温度有关， 在温度变化时会产生改变。 设定在压强为1 atm时， 改变温度值， 观察其对波形的影响。 设定温度为300， 350， 400， 450和500 K， 绘制的谐波图如图7。

图7 不同温度下的二次谐波

从图7中可以看出， 二次谐波信号幅值随温度升高而减小。 温度变化会对S(T)，γL(T，P)，N(T，P)都产生影响。 从HITRAN数据库中的数据可以看到， 随着温度的增加S(T)是非线性减小的。 二次谐波幅值在中心频率处与傅里叶级数A2成正比， 在中心频率处An随温度上升而减小， 因此二次谐波幅值也按照这一趋势变化， 这将导致测量的浓度值减小， 使结果出现偏差。 因此需要采取措施来减小或消除温度变化对测量结果的影响。

因此在本仿真系统中， 再设计增加一个参考气室， 设定其中充入的是浓度确定的标准气体， 之后设置参考与待测的气室所处的环境条件一致， 以此来实现消除温度、 压强变化带来的影响。 将从两个气室当中得到的谐波信号相除， 得到式(12)和式(13)

(12)

(13)

式中， 角标t表示吸收气室， 角标r表示参考气室。 由于K2, t≈K2, r， 则

(14)

由此， 消除了S(T)，N以及线宽的影响， 可以一定程度上提高测试的精度。 采用这种温度补偿方案可以在温度压力波动时测定浓度， 并且在参考气室中的气体浓度已知的情况下， 可以直接得到待测的气体浓度， 而不再需要进行峰值-浓度曲线拟合标定。 按照式(14)计算待测浓度值以直接得到结果如表4所示。

表4 反演气体浓度(体积分数)及误差

柴油机在实际工作中排放， 温度、 浓度会产生一定波动， 这一方法对如何解决这一问题提供了思路。

3.3 调制深度对谱线的影响

在波长调制法中， 低频锯齿波和高频正弦波的波形选择会对得出的一次谐波、 二次谐波波形产生影响， 因此需要进行调试选择一个合适的波形来进行研究。

定义调制系数m

(15)

式(15)中，a为调制深度，γL是洛伦兹线型的半宽。 测量浓度需要一个尽量明显的谐波信号， 因此需要探究不同的调制系数和2f信号的关系。 在调制系数m=0.5， 1， 1.5， 2， 2.5， 3， 3.5和4时， 绘制二次谐波图， 结果如图8。

图8 不同调制系数下的二次谐波

从图8可以看出， 调制系数m直接影响二次谐波信号， 随着调制系数m的增大， 二次谐波信号的线型变得越来越宽， 而峰值则是先增大后减小。 提取与调制系数对应的二次谐波峰值， 绘制调制系数与2f峰值拟合曲线， 如图9。

从图9可以看到， 在m=2.2附近时， 吸收谱线的2f信号峰值最大， 与Reid等和Liu等[10-11]的结论相符合。 因此通常情况下， 为了得到更明显的吸收信号， 选择m=2.2时的调制深度。 但当有邻近谱线干扰时， 可以适当选取较小一些的调制深度， 减小谐波的宽度以减少干扰。

图9 调制系数m与2f峰值的拟合曲线

3.4 调制频率对波形的影响

调制光谱技术可以分为波长调制和频率调制技术， 相较于频率调制， 波长调制技术的调制幅度大， 频率范围一般在kHz数量级， 比较容易实现但是同时也会造成噪声比较大的问题， 可能影响测量精度， 而频率调制技术一般调制幅度小， 调制频率很高， 为MHz到GHz数量级， 信号噪声小， 但同时也会产生实现技术复杂， 成本高的问题。 以下对调制信号的调制频率对波形的影响进行探究。

设定高频正弦调制频率分别为1 000， 2 000， 4 000和6 000 Hz。 二次谐波图形如图10所示。

从图10可以看出， 调整频率后各次谐波的峰值没有明显变化， 在二次谐波当中， 频率较低时系统噪声较大， 图像毛刺较多， 而高频率下噪声较小， 毛刺较少。 考虑到实际实验当中可能使用几万Hz的高频信号， 但是在仿真中这可能会造成仿真时间延长或者波形产生一定失真， 因此在仿真中选用几千Hz的正弦频率即可。

图10 不同调制频率下的二次谐波

对于低频扫描信号， 根据王琳琳等[12]的研究， 正弦波频率和锯齿波频率的调制比在6 000附近时信号幅值最大。 对于扫描信号的幅值， 一般需要能够覆盖吸收峰附近的波数， 但是也不宜太大。

4 结 论

针对于船舶低速机排放检测问题， 根据波长调制技术原理, 利用软件构建了一个NO气体浓度测量模型， 利用模型进行了气体浓度反演， 反演的气体浓度误差在2.5%以内。 分析了环境因素包括温度和压力波动对谱线幅值造成的影响， 采用了参考气室的补偿办法， 不需要重新进行峰值-浓度曲线拟合， 且可以直接得到结果。 通过设置不同的调制参数， 分析了调制参数对信号幅值的影响， 选取了合适的参数范围。 本研究结果为柴油机在线排放测试系统的构建提供了一定的参考价值。