平均分布差异最小化的NIR标定迁移方法研究

赵煜辉， 芦鹏程， 罗昱博， 单 鹏

东北大学秦皇岛分校， 河北 秦皇岛 066000

引 言

近红外光谱(NIR)分析技术具备操作简单、 分析数据速度快、 成本较低、 不污染样品等优势， 已在各领域得到广泛应用， 如农产品生产、 化工产品生产、 食品生产以及环境监测领域[1-4]。 近红外光谱技术在定性分析和快速物质成分定量分析以及实现在线检测方面具有独特优势[5]。 建立多元校正模型是近红外光谱分析技术的重要内容。 即通过一定的数学分析方法， 对近红外光谱数据进行分析建模， 从而达到对一些指标进行预测的目的， 这是一种根据已有样本总结出规律生成模型的方法。 但实际的工业生产中， 测量仪器、 环境和场景通常并不一致， 依据已有近红外光谱数据建立的模型往往并不适用新的仪器采集的数据， 原有模型失效， 并且在测量环境或其他条件变化后， 也需更新模型。

标定迁移是指在不同测量仪器或测量状态下的多元标定模型迁移方法， 通过将从光谱数据迁移到主光谱数据空间， 进而实现主光谱数据模型对从光谱数据模型的预测， 避免重复建模[6-7]。

已有标定迁移方法[8-9]， 主要是通过一组标准样品构建迁移模型， 它需要在主仪器和从仪器上分别测量一组标准样本， 通过一组标准样本来纠正主仪器和从仪器之间光谱的差异。 分段直接标准化(piecewise direct standardization， PDS)， 主仪器的每个波长与从仪器的波长窗口相关， 基于每个窗口间回归系数形成带状迁移矩阵。 实验结果与假设是一致的， 即在各种迁移方法中， 主仪器和从仪器之间的频谱相关性被限制在较小的区域。 PDS的关键是窗口大小的选择和标准样本数目的确定。 在偏差斜率校正(slope and bias correction， SBC)[10]中， 假设不同仪器的预测值之间存在线性关系， 先计算光谱和响应值之间的回归系数； 并用该系数分别计算主仪器和从仪器的预测值； 最后， 在预测值之间进行线性拟合。 SBC算法为一种单变量方法， 因此在测量仪器和测量条件变化引起系统化的光谱差异的情况下， 才能取得较好的效果。 现实生活中， 光谱差异往往比较复杂， 此时它的预测能力是不确定的。 Liang等提出了基于典型相关分析(canonical correlation analysis， CCA)的标定迁移方法成功地校正了不同光谱之间的差异。 首先， 使用主仪器的标定集构建PLS模型； 选取主仪器和从仪器的标定集的一部分作为标准样本； 通过典型相关分析分别提取特征[11]。

标准样本要求主从仪器在相同的环境及条件下测量同一组样本。 工业应用中， 由于标样组分的挥发性及可变性， 使保持标准样品的完整性很难实现[12]， 为此， 需建立标准样本自由的标定迁移模型[13]。

Bouveresse等提出的多元散射校正(multiplicative scatter/signal correction， MSC)[14]是一种信号预处理方法。 MSC计算校准集的平均光谱作为参考光谱， 并在每个光谱和参考光谱之间找到线性关系， 得到斜率和偏差， 利用斜率和偏差来校正从光谱， 虽然不需要标准样本， 但难以处理复杂情况， 且模型性能多数情况较差。

迁移成分回归(transfer component regression， TCR)也是一种无标准的迁移方法[13]， 它结合了迁移成分分析(transfer component analysis， TCA)[15]和普通最小二乘法(ordinary least square， OLS)。 TCA的基本思想是在再生希尔伯特空间中投影两个仪器的数据， 在这个空间中， 主仪器和从仪器的数据分布尽可能的接近， 同时保留原始数据的关键属性。 TCR是一个具有良好泛化能力的稳健模型， 但无法实现更准确的预测。

针对标准样本难以获得和保存， 现有的标准样本自由的标定迁移方法预测能力相对一般的情况， 提出了一种标准样本自由的基于最小化平均分布差异的NIR偏最小二乘标定迁移方法(minimizing mean distribution discrepancy Calibration Transfer for NIR， MCT)。 此方法在不考虑从仪器标准样本的情况下， 为去光谱数据的多重共线性， 首先假设存在一个适用于主从仪器的偏最小二乘子空间， 该子空间通过后续优化主从仪器在此空间中的分布差异获得， 接着将主从仪器光谱数据分别投影到该假设的公共子空间； 然后引入平均分布差异最小化算法， 即分别给出主从光谱数据在子空间的平均分布(中心点)表示函数， 最小化两个光谱平均分布(中心点)的差异， 并最大化投影后主仪器光谱的协方差， 目的是使主仪器投影后的数据具有最大相关性， 推导求解出最佳子空间； 最后， 将主光谱样本和从光谱预测样本分别投影到该子空间中， 利用主光谱数据得到回归模型， 通过此回归系数计算出从光谱预测浓度。 该方法无需标准样本的获取， 便能缩小主从仪器数据间的分布差异， 同时对比现有标准自由迁移方法， 更加简单高效， 并具有更好的预测性能。 本文使用玉米数据集和小麦数据集， 将MCT的性能与SBC， PDS， CCACT， TCR和MSC进行比较。

1 理论知识

1.1 定义符号

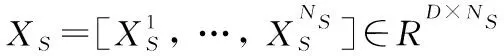
1.2 偏最小二乘法

在化学计量学中， 偏最小二乘算法(partial least square, PLS)是一种很有效的多元标定方法。 PLS算法结合了多元线性回归、 主成分分析、 典型相关分析的优点， 被广泛用于建立输入空间和响应空间之间的关系。 PLS通过分数向量建立输入空间和响应空间之间的关系。 PLS模型的目的是确保最佳的潜变量数量。 潜变量是原始变量的线性组合。 它包含了关于X和y之间关系的最大相关信息。 在数学上， 由式(1)表示目标函数

subject to ‖w‖2=1

(1)

其中w代表权重向量。 该目标函数是在一个约束下的最大化问题， 可以通过拉格朗日乘数法进行求解。

在这个算法中， 第一个权重向量必须是矩阵XTyyTX的主要的特征向量。 从第二个潜变量开始， 它要求接下来的潜变量与前面的潜变量正交(不相关)。 因此， 接下来的权重向量也是矩阵的主要特征向量， 重复这一系列步骤直到收敛。 模型被构建通过如下等式

其中T是得分矩阵，P和Q分别代表X的载荷矩阵和y的载荷矩阵向量;E和F分别表示残差矩阵;A是PLS模型潜变量的最佳数量。

最后， 模型的回归系数β可写如式(2)

β=W(PTW)-1QT

(2)

式(2)中，W=[w1,w2, ……,wA]为权重矩阵。

1.3 模型建立

(3)

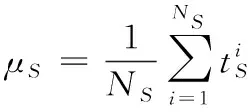
令T=PTX， 最小化问题式(3)可以重新表示为

(4)

为了学习得到这样一个能使式(4)中的平均分布差异最小化的基变换矩阵P， 还应确保投影后的源数据XS与源数据浓度yS之间的关系具有最大相关信息。 因此， 对于源域的数据， 合理的做法是将以下项最大化

(5)

在求解式(5)时可以看出， 源域数据的协方差在新学习的子空间中已经被最大化， 那么在这一过程中就保留了尽可能多的可用信息。

结合式(4)和式(5)， 可以得到以下优化目标

(6)

(7)

在式(7)的最大化问题中，P有许多的可能解(即并非唯一解)， 为了保证解的唯一性， 式(7)施加了一个等式约束， 这样就可以写成

s.t.Tr(PT(μS-μT)(μS-μT)TP)=η

(8)

其中η是一个常数。

为了解出式(8)， 将其改为拉格朗日函数， 见式(9)

γ(Tr(PT(μS-μT)(μS-μT)TP)-η)

(9)

其中γ表示拉格朗日乘子系数。

接下来， 将L(P,γ)对P求偏导， 令其偏导数为0， 就得到

AP=γP

(10)

由此得出， 最优子空间P*表示矩阵A特征值分解后的前k个最大特征值所对应的特征向量， 而γ表示是一个对角矩阵， 对角线上的值分别为前k个最大特征值。

为了便于实现， 将所提出的MCT算法归纳到下列算法描述中。

1.4 MCT的算法描述

输出： 回归系数β。

(2) 计算矩阵A

(3) 根据公式AP=γP对A进行特征值分解。

(4) 得最优子空间P*=[p1,p2, …,pk]

(5) 计算投影到子空间后的矩阵

(6) 计算回归系数

MCT算法到此结束。

(7) 预测

2 实验部分

为了验证算法的准确性和实用性， 使用玉米数据集和小麦数据集作为实验对象， 对数据集进行了数据分析， 来检验MCT方法的性能。

2.1 数据集介绍

第一个数据集是在三个近红外光谱仪(M5， MP5和MP6)上测量含有80个样本的玉米数据集。 每个样品含有四种成分： 水分， 油， 蛋白质和淀粉。 波长范围为1 100～2 498 nm， 间隔为2 nm(700个通道)。 该数据集可以从http://www.eigenvector.com/Data/Corn/下载。 使用这三个近红外光谱仪和玉米数据集成分中的水分进行研究讨论。 仪器M5和仪器MP5之间的光谱差异如图1(a)所示； 仪器M5和仪器MP6之间的光谱差异如图1(c)所示； 仪器MP5和仪器MP6之间的光谱差异如图1(e)所示。 其中横轴表示波长， 纵轴表示吸光度差异， 曲线表示光谱样本。

图1 不同仪器之间的光谱差异

小麦数据集由制造商A的三个仪器(A1， A2和A3)测量的248个样本组成。 数据集只提供蛋白质参考值。 波长范围为730～1 100 nm， 间隔为0.5 nm。 可在http://www.idrc-chambersburg.org/获取。 使用了三个近红外光谱仪和蛋白质含量进行研究讨论。 仪器A1和仪器A2之间的光谱差异如图1(b)所示； 仪器A1和仪器A3之间的光谱差异如图1(d)所示； 仪器A2和仪器A3之间的光谱差异如图1(f)所示。 其中横轴表示波长， 纵轴表示吸光度差异， 曲线表示光谱样本。

2.2 数据处理

通过Kennard-Stone算法将玉米数据集的80个样本分成两组： 80%用做标定集样本， 20%用做测试集样本； 将小麦数据集的248个样本分成两组： 80%用作标定集样本， 20%用作测试集样本。 对于有迁移标准的迁移方法， 使用Kennard-Stone算法在标定样本上选择若干个标准样品。

2.3 性能评估

在该实验中， 均方根误差(root mean square error, RMSE)被用作参数选择和模型评估的指标。 此外， RMSEC表示标定集的训练误差， RMSEP表示测试集的预测误差。 RMSE计算方法写为

(11)

文中RMSEP代表从仪器测试集。

3 结果与讨论

选用玉米和小麦光谱数据集检验模型的性能。 使用SBC， PDS， CCACT， MSC和TCR五种方法进行对比实验。 对于SBC， PDS， CCACT和MSC算法均采用PLS算法作为主体算法， 使用主仪器的光谱数据建立多元标定模型作为参考模型， 用于对从仪器的待测样本进行预测。 实验结果主要包含两个部分： (1) MCT和对比方法的RMSEC和RMSEP比较； (2) MCT和对比方法预测结果的拟合能力示意图。

MCT和其他五种标定迁移方法的标定误差和预测误差被展示在表1和表2中。

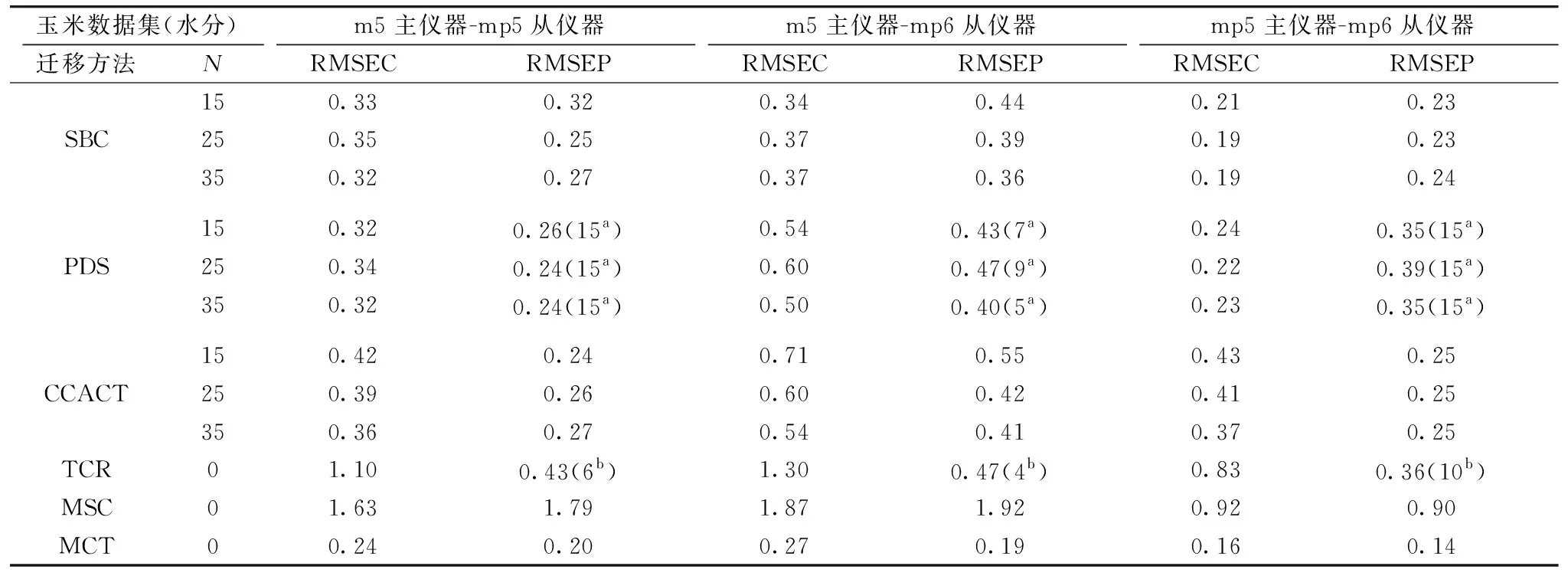
表1 SBC, PDS, TCR, CCACT, MSC和MCT六种迁移方法在玉米数据集下的RMSEC， RMSEP

表2 SBC, PDS, TCR, CCACT, MSC和MCT六种迁移方法在小麦数据集下的RMSEC， RMSEP

玉米数据集实验结果分析如下：

对于仪器MP5到仪器M5的标定迁移， MCT的RMSEP小于TCR和MSC这两种标准样本自由的方法， 同时也小于SBC， PDS和CCACT这三种有标样的RMSEP， 并且MCT的RMSEC也低于其他五种迁移方法。 对于仪器MP6到仪器M5的标定迁移， 由SBC， PDS， CCACT， TCR和MSC获得的最低RMSEP分别为0.36， 0.40, 0.41， 0.47和1.92。 表1中列出的结果清楚地表明MCT具有比其他五种方法更低的RMSEP和RMSEC。 对于从MP6到MP5的标定迁移， MCT再一次达到了最小的RMSEP和RMSEC。

小麦数据集实验结果分析如下：

对于仪器A1到A2的迁移， 当标准样品数为35， 25和35时， SBC， PDS和CCACT分别取到最小值。 从表2中能够看出方法MCT的RMSEC和RMSEP都小于其他五种方法的最佳结果。 对于仪器A2到A3的迁移， 当标准样品数为35时， SBC， PDS和CCACT均取到最小值， 由表看出MCT的RMSEP均小于其余五种方法。 对于仪器A3到A2的迁移， MCT再一次达到了最小RMSEP和RMSEC。

这六组对比实验可以看出， MCT模型在通常情况下能够取得最优的预测效果， 并具有更好的鲁棒性。

图2—图4和图5， 图6分别显示了在玉米集和小麦集中， 六种不同的标定迁移方法的预测值与测量值的关系图。 预测浓度和测量浓度之间的零差异， 将会使得样本点在直线上。 对于有标准样本的标定迁移方法， 选取预测性能最优时的数据用于比较， 以便更加充分的体现出MCT能够取得良好的预测性能。 表3是六种迁移方法的预测值与测量值曲线拟合斜率表。

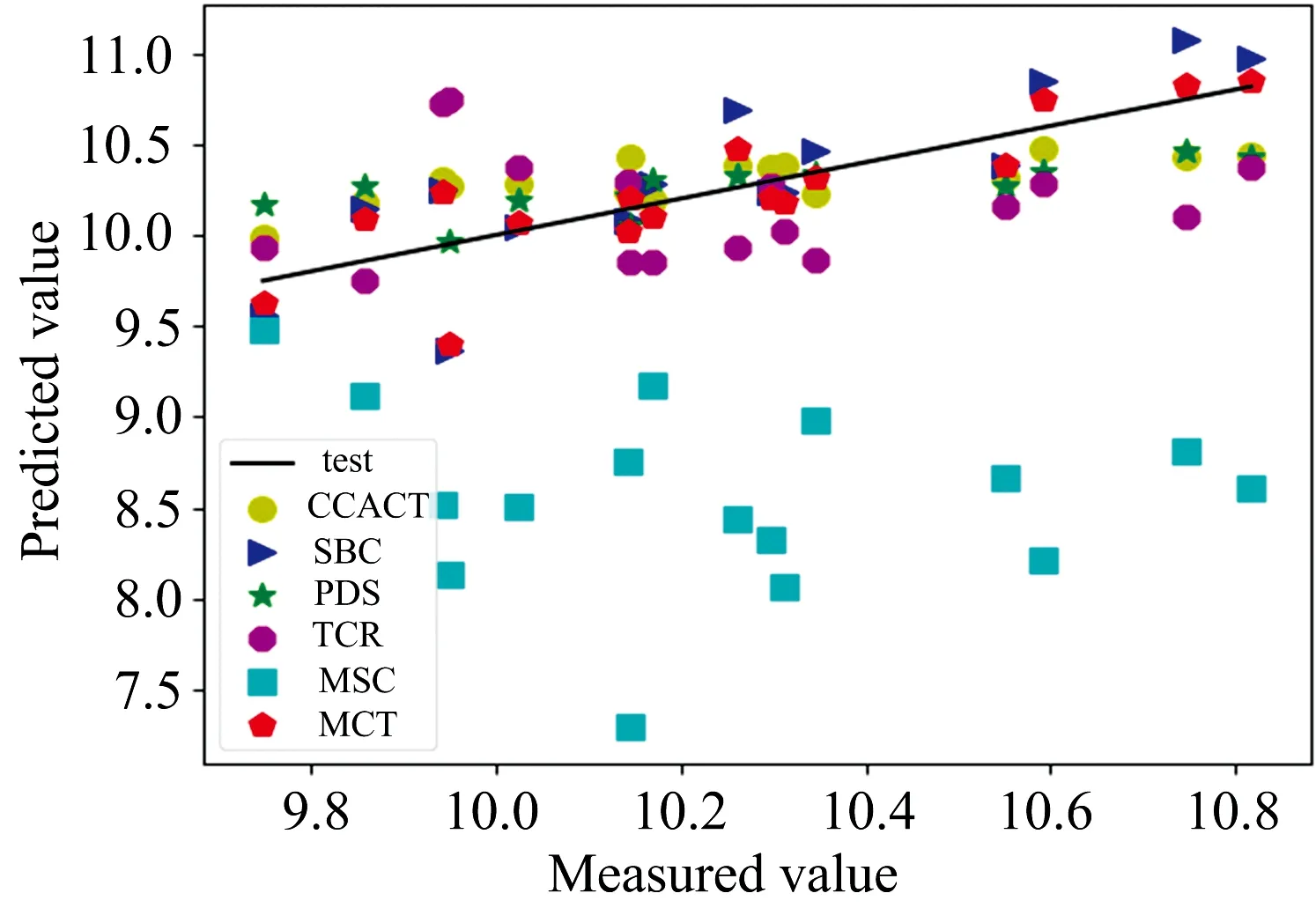
图2 SBC， PDS， CCACT， TCR， MSC和MCT六种方法在仪器M5和仪器MP5之间预测结果的散点图

图3 SBC， PDS， CCACT， TCR， MSC和MCT六种方法在仪器M5和仪器MP6之间预测结果的散点图

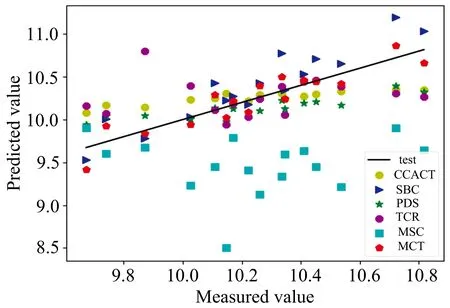
图4 SBC， PDS， CCACT， TCR， MSC和MCT六种方法在仪器MP5和仪器MP6之间预测结果的散点图

图5 SBC， PDS， CCACT， TCR， MSC和MCT六种方法在仪器A2和仪器A1之间预测结果的散点图

对于玉米数据集表， 图2—图4显示MCT方法的预测结果相比其他五种迁移方法具有更好的预测性。 根据表3中的数据也可证明MCT相比其他方法更加接近直线。 通过上面的陈述， 可以得到结论： MCT能够在玉米集所有模型中实现最佳的预测性能， 同时具有更好的泛化能力。

对于小麦数据集， 图5—图7及表3中均可以看出， MCT的样本点更加接近直线， 相比其他五种方法， 其能够达到更好的预测效果。 通过上述对比， 可以很容易地得到结论： MCT在小麦集的所有模型中能够实现最佳的预测性能， 同时具有更好的泛化能力。

图7 SBC， PDS， CCACT， TCR， MSC和MCT六种方法在仪器A2和仪器A3之间预测结果的散点图

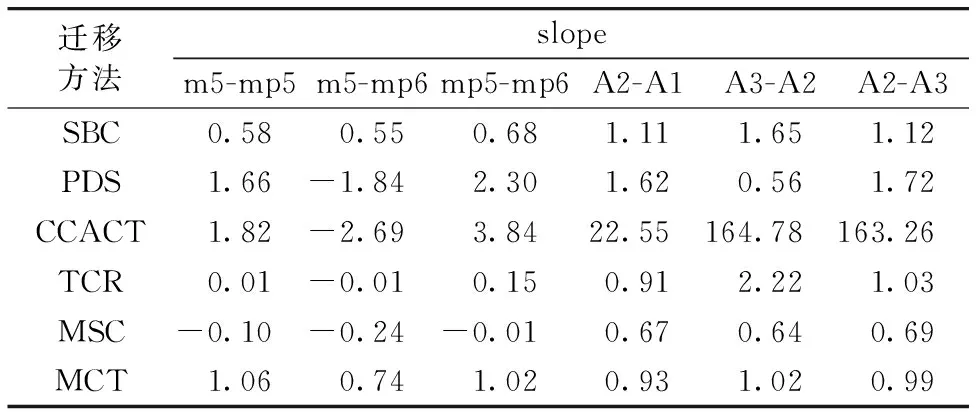
表3 SBC, PDS, TCR, CCACT, MSC和MCT六种迁移方法预测结果斜率对比表

3 结 论

提出了一种基于最小化平均分布差异的标准样本自由NIR偏最小二乘标定迁移方法。 该方法学习了如何找到能够使主从仪器数据投影后， 两域平均分布差异最小的同时， 还能使主光谱投影后的数据相关性最大的一个公共子空间。 在该子空间中， 主从仪器的数据分布得到了极大的校正， 能够使从仪器共用主仪器模型， 实现标定迁移。

在玉米和小麦数据集中， 使用SBC， PDS， CCACT， TCR和MSC作为对比实验来检验MCT方法的性能， 并且所提出的方法(MCT)通常实现了最佳的RMSEC和RMSEP。 结果清楚地表明， MCT能够成功地用于校正在不同仪器上测量的光谱之间的差异。 对于SBC， PDS和CCACT这三种迁移方法， 它们需要标准样品建立迁移模型。 在TCR中， 从仪器样品还需要少量的参考值。 这两个条件在实际应用中， 都会产生很昂贵的代价， 甚至无法满足这一条件。 因此， 当标准样品在实际应用中不可获得时， 同时对比现有标准样本自由方法， MCT是一种有效的标定迁移方法。