腰部外骨骼线性自抗扰控制研究*

季心宇 吴洪明 王大帅 徐克锋 孙健铨

1武汉理工大学 武汉 110016 2 广东省机器人与智能系统重点实验室 深圳 518055

3中国科学院人机智能协同系统重点实验室 深圳 518055 4 粤港澳联合实验室 深圳 518055

0 引言

骨骼肌肉疾病是许多工业国家（例如中国、印度和美国）中最常见的疾病。对工人的生活质量和公司的生产力有重大影响。在物流、建筑和医疗康复行业中，患有腰部疾病的工人占比分别为84%、75%和67%[1]。随着腰部肌肉疾病发病率不断增加，该问题值得关注。针对该问题，研究人员已经提出了许多解决方案。其中，腰部动力外骨骼机器人方面的研究工作值得重点关注[2]。

腰部动力外骨骼机器人主要由动力源、机械结构和传感器组成。现有腰部动力外骨骼系统包括日本筑波大学的HAL外骨骼机器人[4]、意大利技术研究院的ROBO-MATE外骨骼机器人[5]及中国科学院深圳先进技术研究院的SIAT-WEXv2外骨骼机器人[6]。HAL外骨骼是以肌电信息作为控制的信号流，由无刷伺服电机提供动力，使用高性能处理器来控制外骨骼。ROBOMATE外骨骼机器人以穿戴者运动信息为信号流，串联弹性驱动器为动力源，使用MYO肌电手环传感器检测手部肌电信息，并与交互力信息结合来控制外骨骼。SIATv2外骨骼机器人也是以穿戴者运动信息作为信号流，使用伺服电机作为动力源，采用基于李雅普诺夫稳定性的扩展卡尔曼滤波作为观测器来预测外界扰动，使用控制器来补偿物体对系统的影响。

无论是添加传感器，还是以扩展卡尔曼滤波器的方式观测物体的质量变化对系统的影响，都是一种局部观测器。对于腰部外骨骼机器人而言，扰动量不仅仅包含了物体质量变化对系统的扰动和人机交互之间的扰动，还有其他未知因素对系统的干扰。对于外骨骼系统的补偿问题，这2种方式来无法完全消除扰动量。因此，对腰部外骨骼机器人而言，一种全局观测器的使用尤为重要。韩京清[7]提出了非线性自抗扰控制器，该控制器包含一种全局扰动观测器，该观测器可以观测全局的扰动变化。但是对系统调试来说，非线性自抗扰控制的参数较多。为此，高志强[8]提出了线性自抗扰控制的方法。该方法只需调整2个参数，就可以设计出自抗扰控制器。

为了解决搬运物体质量变化对腰部外骨骼系统影响的问题，本文使用线性扩张扰动观测器（LESO）估计外骨骼系统的总扰动，即观测物体质量对系统的扰动和外骨骼系统自身的扰动。其次，利用线性自抗扰控制器（Ladrc）来消除总扰动，将控制器模型转换成串联积分器的形式，通过比例-微分控制外骨骼系统。

1 腰部外骨骼机器人建模

由于在整个穿戴者搬运物体的整个周期中，穿戴者双腿的动作保持一致。因此，从冠状面看，腰部外骨骼系统的简化模型如图1所示。m1、l1为腰部外骨骼上肢的质量、杆长，lc1为关节电机与上肢重心的距离，F1为人机交互力及搬运物体质量对外骨骼的总作用力，τ为电机驱动系统的驱动力矩，q1为关节电机的角度值。

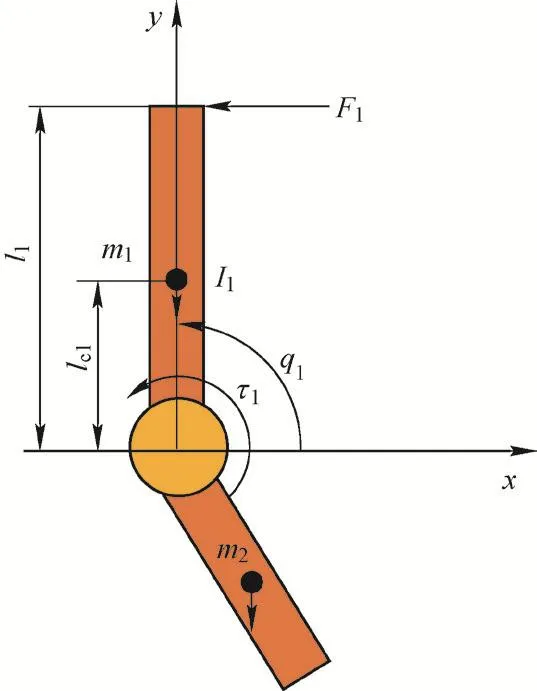
图1 腰部外骨骼简化模型

通过拉格朗日动力学方程[9]，可得

式中：T为外骨骼动能，V为外骨骼的势能，L为外骨骼的能量差。

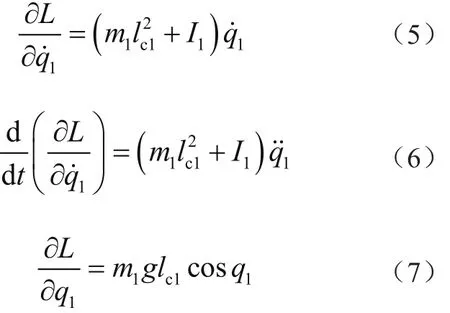
整理式（4）～式（7），可得

式中：I1为转动惯量。

2 线性自抗扰控制器

本文采用扩张扰动观测器来观测全局的不确定性。但是韩京清[7]提出的非线性扩张扰动观测的可调参数过多。为此，本文将采用线性扩张扰动观测器估计扰动量。

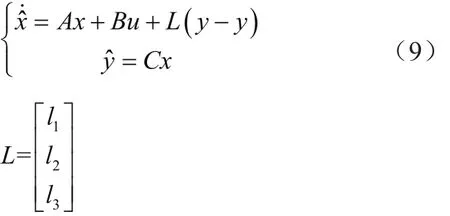
式中：L为观测器增益。

整理式（9）可得

整理式（10）得其状态空间方程为

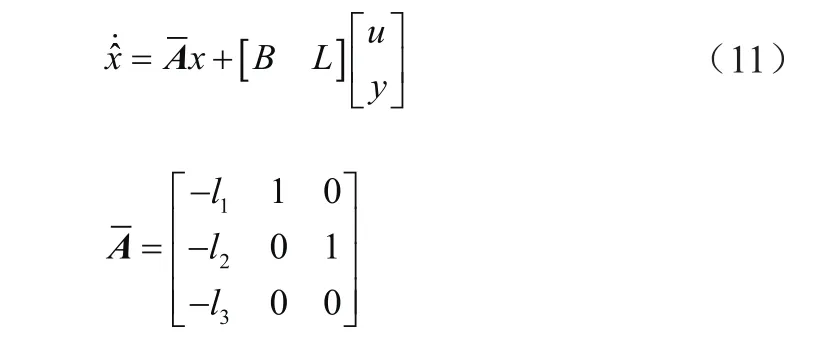
将极点配置到-ω0，使得所有参数为该处得传递函数，即

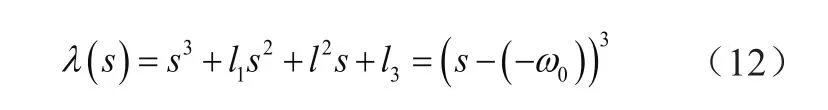
由此可得，l1=3ω0，l2=3ω02，l3=ω03，配置在系统s平面的左半平面，实现观测器鲁棒地估计扰动。

因此，取观测器状态变量为［x1x2x3］，观测器的输入为［u y］，其输出为。扩张观测器以系统的输入和输出为输入，以系统输出、其输出的变化率和系统扰动总和的估计值为输出。

本文介绍的腰部外骨骼扩张观测器的状态变量的矩阵表达式为

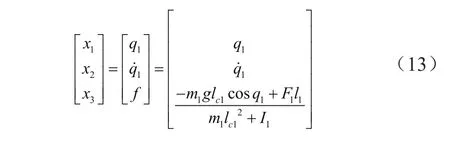
腰部外骨骼扩张观测器中的状态变量的变化率为

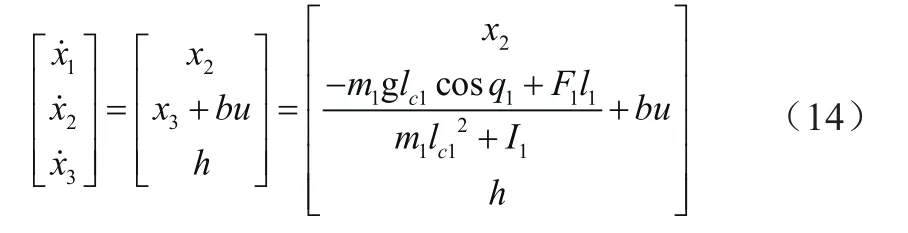
线性扩张观测器的状态空间方程为

由于LESO可以估计搬运物体质量、穿戴者的交互作用及系统模型的不确定性，所以本文可通过动态补偿来消除扰动对系统的影响，结合自抗扰控制技术来设计线性自抗扰控制器。

根据观测器所获得的信息，有

通过扩张观测器对扰动总和的观测，系统被简化成串联双积分器的形式。

控制律取

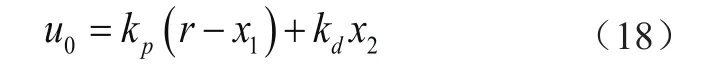
式中：r为目标轨迹。

因为经过了扩张观测器，系统简化为无零点的二阶双积分器系统。为了选择合适的kp和kd，将系统转化成为二阶传递函数的形式为

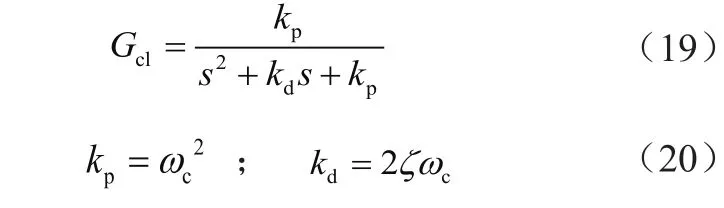
式中：ωc为闭环系统的自然震荡频率；ζ为阻尼比，选择合适的阻尼比使系统不出现震荡的情况，本文选用ζ=1 的阻尼比[8]。

3 仿真

以腰部外骨骼简化模型为研究对象，采用线性自抗扰方法设计控制器，以验证该方法在系统模型存在扰动及不确定性下的有效性。

如图2所示的线性自抗扰控制器方框图搭建仿真模型，其中腰部外骨骼系统相关参数为：质量m1=3.4 kg，连杆长度l1=0.46 m，连杆重心长度lc1=0.20 m，转动惯量 I1=0.046 kg·m2。

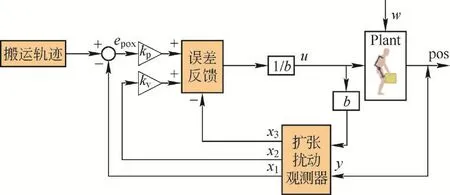
图2 线性自抗扰控制器方框图

在仿真过程中，外骨骼的跟踪轨迹近似于五项式方程[10]

式中：t为搬运周期时刻；系数a、b、c和d可以通过边界条件来计算。

对式（21）分别进行一次、二次求导得

当穿戴者与外骨骼直立时，将q设置为90°。弯腰举起重物的起始角度设置为0°，角度q作为初始条件，将其代入式（21）（22）以确定系数并获得期望的外骨骼轨迹和角速度。通过Matlab/Simulink软件，获得数据结果如图3～图6所示。

线性自抗扰控制器能否实现较好的控制效果，关键在于动态线性化补偿能否很好抵消含内外扰动的加速度项。其中f（q1，ω（t））为含有内外总扰动的加速度项，对含有总扰动的加速度项的估计即状态观测器的输出x1、x2、x3，用此估计值来补偿总扰动。图3所示为关节中含有的总扰动的加速度项及其估计的曲线图，其中表示为f （q1，ω（t）），实线表示为扩张状态观测器的输出 x1、x2、x3。

如图3所示，随着搬运物体质量的不断增加，图3的蓝线代表的实际扰动量也随之增加。为了估计总扰动量，本文使用的线性扩张扰动观测器对实际扰动量进行估计。进一步研究图3的曲线，虽然搬运物体的质量不断增加，但红线代表的估计扰动量一直逼近于实际扰动量。由此可知，本文中使用的线性扩张扰动观测器可估计实际的扰动量，对进一步设计控制器提供了较大程度的帮助。在线性扩张扰动观测器的基础上，本文采用Ladrc对腰部外骨骼机器人系统进行控制。

图3 实际扰动与LESO观测扰动对比

为了更好地说明Ladrc控制方法的优越性，在仿真中，加入相同搬运物体质量，将Ladrc与PID控制方法进行比较。根据外骨骼的工程需要（搬运0 kg物体时，关节电机角度误差控制在1°以内）和PID调参经验，选择kp=100、ki=10、kd=5。由此可知，在该参数下PID的控制下的轨迹误差小于1°。该仿真误差满足了实际需求。因此，仿真将在该PID配置参数下，对外骨骼模型进行分析研究。而对于线性自抗扰控制器的参数选取，由给定的参考信号特性以及应用的对象决定。ADRC控制器的参数选为ωc=300、ω=350、b=5.4。

由图4～图6可知，基于Ladrc控制方法的外骨骼跟踪轨迹与理想轨迹基本重合，且误差均保持在0.6°内。故Ladrc控制方法具有很好的轨迹跟踪能力。由图3可知，总扰动的估计与实际的总扰动项变化趋势近似一致，增强系统的干扰估计能力。通过比较图4～图6，PID控制器最大的角度误差随着质量增加而不断增大，而Ladrc控制器的最大角度误差，始终保持0.6°的范围内。与此同时，随着搬运物体质量的增加，PID控制器的输入量呈现先增加后减少的趋势，而Ladrc控制器的输入量随着扰动量的变化而变化，其补偿外界对系统的扰动量。最后，通过比较图4～图6控制方法跟踪速度的结果，可看出线性自抗扰控制器呈现平滑跟踪的轨迹，而PID控制器随着搬运物体质量的增加呈现出了跟踪不稳定的趋势。对于外骨骼系统而言，平滑的轨迹跟踪与速度跟踪可避免对穿戴者的二次伤害。由此说明，在搬运物体质量变化的情况下，Ladrc控制方法要优于PID控制器。综上所述，本文设计Ladrc的控制器具有较好的抗扰动能力，使得腰部外骨骼具有精确的轨迹跟踪效果。

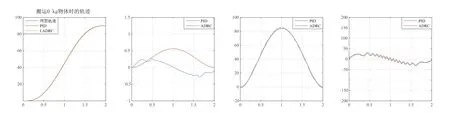
图4 腰部外骨骼PID与Ladrc控制器对比（搬运物体的质量为0 kg）

图5 腰部外骨骼PID与Ladrc控制器对比（搬运物体的质量为10 kg）

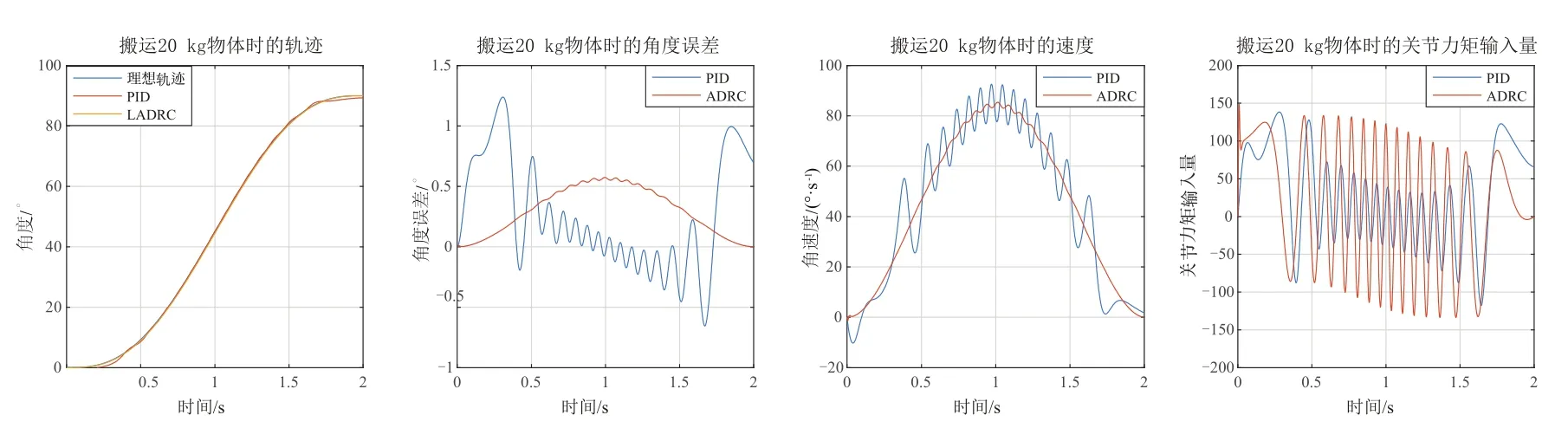
图6 腰部外骨骼PID与Ladrc控制器对比（搬运物体的质量为20 kg）

4 结论

在本文中，腰部外骨骼是一个非线性且强耦合的动态系统，具有很大的不确定性。与此同时，该系统具有相对重复的运动轨迹。文中提出了一种基于线性自抗扰控制的控制算法。该算法由线性扩张扰动观测器作为全局观测器。该观测器可以估计穿戴者与外骨骼之间的相互作用力以及外骨骼的关节位置和速度。腰部外骨骼使用该控制算法，以平滑的关节速度，精确地跟踪搬运轨迹。并且在穿戴者搬运物体时，外骨骼可为其提供外部辅助力矩。从而，该外骨骼提高穿戴者的工作效率，降低穿戴者患腰椎疾病的风险。