基于张拉整体结构的可移动折纸机器人结构设计

孙建伟， 王 贺， 李晓东

(1.长春工业大学 机电工程学院， 吉林 长春 130012;2.长春工业大学 工程训练中心， 吉林 长春 130012)

0 引 言

折纸机构[1]最早起源于折纸艺术，机构学家从中受到启发，将纸板折叠可形成一定数目的折痕和纸板单元，将纸板单元等效为构件，折痕等效为转动副，纸板则等效为一个具体机构，即折纸机构。在折纸机构应用中，目标是利用折纸机构具有质量轻、存放体积小和便于运输的结构特点[2-4]。

近年来，很多国内外学者与研究机构依据折纸机构提出多种行走机器人，并且在其设计、材料和制造方面做了大量工作[5-11]。其中将折纸机构运用到仿生爬行类机器人的方法得到了深入研究[12-15]。但是对于折纸机构的折叠驱动问题，由于机构折叠顺序、角度和方向等参数多，驱动相对困难，为折纸机器人折叠提供有效方法还比较少，因此，完善折纸机构驱动的理论方法需要在完成有效折叠的同时，尽可能减少对折纸机构折叠不影响的机构参数。在折纸机构中，刚性折纸机构是应用最为广泛的。

文中通过一种可爬行与转向的折纸机器人为设计目标，在设计一种具有双稳态折纸机构的基础上，提出了将张拉整体结构应用到折纸机构的驱动上，通过对张拉整体结构驱动的折纸机器人建立结构模型、运动仿真和搭建物理样机，实现折纸机器人的爬行与转向。折纸机器人的长度可以完成从192 mm到144 mm的变化，理论展收比为0.75，爬行速度可达40 mm/s。

1 折纸机构折叠单元设计与分析

标准单顶点五折痕构型及折叠构态如图1所示。

(a) 折叠单元平面展开 (b) 折叠单元折展图1 单顶点五折痕

将图1中的五条折痕控制3条折痕转角,可以确定两种折纸机构构型形状。折叠单元的折痕交点即顶点为n，Pi为第i个刚性平面，排序方向为逆时针。折痕分别为f1、f2、f3、f4、f5，其中f1、f2、f4为山折痕(折痕为山峰)，f3和f5为谷折痕(折痕为山谷)。αij为折痕夹角，即折痕i与折痕j的夹角。该设计结构简单，能够实现两种折叠状态，完成可移动折纸机构两自由度移动构想。

坐标变换过程如图2所示。

(a) 以z1为旋转轴坐标变换 (b) 以x2为旋转轴坐标变换图2 坐标变换过程

将图2中折痕内交点作为原点，以f1为x1轴，方向由原点向外，y1轴垂直于x1轴，z1轴方向与各面垂直组成坐标系。其中ρ1为折痕转角，αij为折痕夹角。将坐标系O-x1y1z1绕z1轴按逆时针方向转动α12,得到O-x11y11z11，见图2(a)，变换后的x1与x2重合。再将坐标系O-x11y11z11绕x2轴沿逆时针方向转动ρ1，见图2(b)，得到O-x12y12z12。此时两坐标系O-x12y12z12与O-x2y2z2重合。同理，按照此类坐标变换方式，将坐标系O-x1y1z1分别绕z1、x2、z2、x3、z3、x4、z4、x5、z5、x1进行10次旋转坐标变换后，O-x1y1z1旋转变换到与自身重合。

将折痕夹角与折痕转角的标注简化，折叠单元的折痕夹角与折痕转角示意图如图3所示。

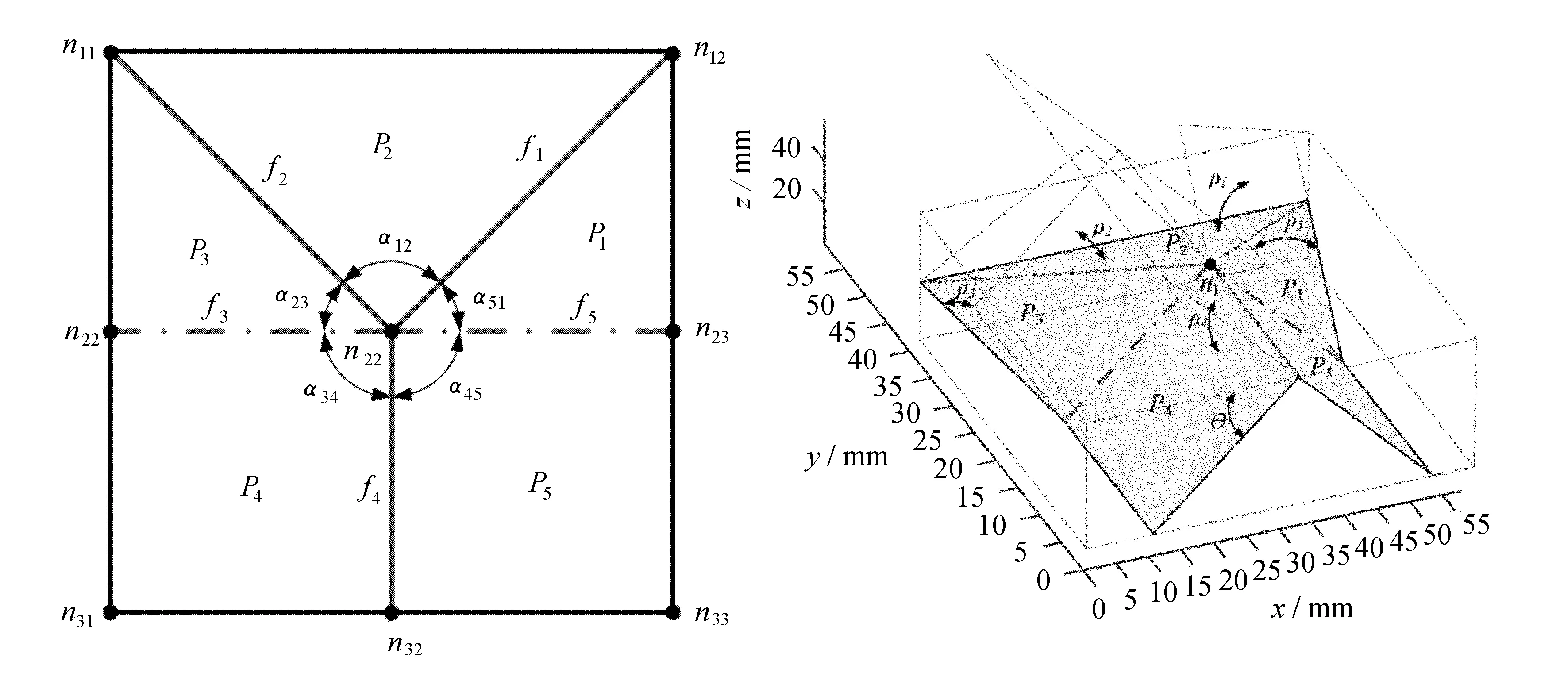
(a) 折痕夹角 (b) 折痕转角图3 折叠单元的折痕夹角与折痕转角示意图

由于谷折痕对称且大小相等，文中定义谷折痕与水平面的夹角，即谷折痕转动角为输入角θ，为可控输入值。由于折叠单元水平放置于地面，折叠单元折叠后的ln22n31、ln23n33分别与水平面接触，即

θ=π-ρ4。

(1)

为了避免折叠过程中相邻两刚性面间的结构干涉，需要将折痕转角ρ的范围限制为

-π<ρ<π。

(2)

通过坐标系的多次旋转变换联系起来，可以得到折痕转角关系方程

Z(α12)X(ρ2)Z(α23)X(ρ3)Z(α34)X(ρ4)×Z(α45)X(ρ5)Z(α51)X(ρ1)=I,

(3)

式中：X(ρ)----绕x轴转动ρ角的旋转变换矩阵,

(4)

Z(α)----绕z轴转动α角的旋转变换矩阵,

(5)

I----单位矩阵,

(6)

分析建立了单顶点五折痕折纸机构折痕转角之间的关系方程，对于折痕数为n的单顶点刚性折纸机构构型，均可使用该方法建立折痕转角关系方程。

2 可移动折纸机器人构型设计

折叠单元的两种折叠构态如图4所示。

图4 两种折叠构态

单顶点折纸机构的自由度等于折痕总数减3，则对于折痕数为5的单顶点折纸机构，在确定任意2个折痕转角之后，剩余3个折痕转角可通过式(1)求得。为了保证可移动折纸机器人行走的稳定性和可双向移动的对称性，折叠单元在折叠运动时折痕夹角α51=α23,α34=α45和折痕转角ρ1=ρ2,ρ3=ρ5。

其中，如图4中折叠构态2，由于折痕夹角α51=α23,α34=α45和折痕转角ρ1=ρ2,ρ3=ρ5，建立各折痕转角的关系方程见式(3)。

式中

(7)

其中，ρ4可由输入角θ得到，ρ1可由厚板化折纸机构确定。即ρ1(ρ2)、ρ4为已知折痕转角，建立如下各折痕转角关系方程

Z(α12)X(ρ1)Z(α23)X(ρ3)Z(α34)X(ρ4)×

Z(α45)X(ρ3)Z(α51)X(ρ1)=I。

其中各折痕夹角为已知，即当α12=90°、α23=α51=45°、α45=α51=90°时,求取折痕夹角ρ3(ρ5)

(8)

在折痕转角ρ1(ρ2)、ρ4确定时，ρ3(ρ5)可以由式(6)得出，既而得到单顶点五折痕折叠单元的折叠构态。

经计算得出α12为90°时,折叠单元有效折叠最高，采用α12为90°的折叠单元，在确定输入角θ和折痕转角ρ1可求出其余折痕转角，见表1。

表1 α12=90°时折痕夹角下折痕转角计算结果 (°)

建立可移动折纸机器人数学模型，在单顶点五折痕折纸机构构型的基础上，对折叠单元进行改进，使得折叠单元更加适合组装的同时，保持了刚性折叠的特性，为折叠单元拼接和机器人刚性折叠运动做基础。单顶点五折痕折叠单元结构性对称，重复性强，参考系坐标易于选取，空间各点在折痕转角关系方程下得到，可以完成折叠单元建模，如图5所示。

(a) 折叠单元构态1

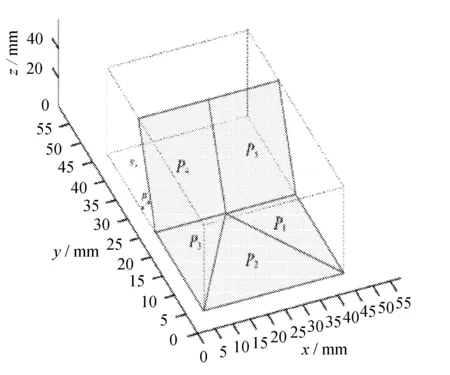
(b) 折叠单元构态2图5 折叠单元建模

将两组折叠单元组合可实现两种对称折叠稳态,如图6所示。

(a) 前后足 (b) 左右足图6 两折叠单元组成的两种折叠构态

折纸机器人折叠模型如图7所示。

图7 折纸机器人折叠构型

在前后行走时,前后足与地面接触，左右足抬起;在左右行走时,左右足与地面接触，前后足抬起。行走时减少了机器人其余部分与地面的摩擦，减少能量损耗，提升行走速度。

3 基于张拉整体结构的可移动折纸机器人行走实验

3.1 折痕夹角与折痕转角选择

不同折痕夹角的折叠单元如图8所示。

图8 不同折痕夹角的折叠单元

根据折叠单元构型展收比最佳原则,以及考虑折纸机构稳定性对不同折痕夹角的折叠构型进行选择。图8是折痕夹角α12分别为120°、90°、60°的折纸机构单元，对应的折痕夹角α23(α51)分别为30°、45°、60°。

基于张拉整体驱动的折纸机器人，由于张拉整体结构尺寸的限制与实际装配要求，折纸机器人行径(展收比)不仅与折痕转角和张拉单元的位置关系有关，还受到折纸机构构型与张拉整体结构驱动单元位置关系的影响。张拉整体结构驱动如图9所示。

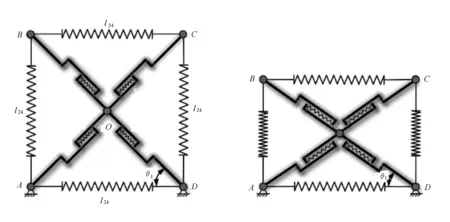
图9 张拉整体结构

根据不同姿态下的张拉整体结构驱动单元与折纸机构的位置约束条件，匹配合适的轨道拉簧组合。其中短拉簧长度为l1i(i=1，2，3，4)、长拉簧长度为l1j(j=1，2，3，4)、短导轨长度为ld。传动限位结构的不等式约束条件如下：

(9)

(10)

ld>l11。

(11)

其中张拉整体结构驱动中最大拉伸夹角θ3为短导轨与长拉簧的极限接触位置，即

(12)

式中：r1----短导轨半径;

d1----短导轨与拉簧极限接触时短导轨到端点的距离。

3.2 弹簧刚度匹配

折纸机器人质量很轻，垂直方向上所受重力可以忽略不计，只需计算水平方向上的受力分析即可，从而进行相应弹簧刚度匹配。根据平行四边形定则，折纸机器人完全展开姿态时每组张拉驱动单元中各弹簧水平方向的合力最小，随着折纸机器人折叠姿态逐步收拢，各弹簧受到合力逐渐减小。因此,匹配的弹簧刚度只要能够保证折纸机器人在完全展开姿态时稳定运行，就可以满足其他姿态下折纸机器人的稳定行走。

令实验折纸机器人驱动电机输入力为F输入， 短弹簧受到拉力为Fi(i=1,2,3,4)，弹簧刚度系数为Ki，短弹簧变化量为Δl1i=l1i-l1i*，弹簧EF受到拉力为FEF。长弹簧受到拉力为Fj(j=1,2,3,4)，弹簧刚度系数为K2，长弹簧变化量为Δl1j=l1j-l1j*，弹簧AB受到拉力为FAB。由胡克定律得到：

Fi=K1Δl1i,

(13)

Fj=K2Δl2j。

(14)

由于垂直方向上的作用力为折叠折纸机器人所需力，这里将折痕视为零厚度，垂直方向上的折叠所需力为零，即只分析水平方向力即可。

当完全展开时，A点水平方向静力平衡方程为

FAB=FACcosθ1=2K1Δl1icosθ1。

(15)

当输入力F输入作用在A点时，A点水平方向静力平衡方程为：

(16)

(17)

式(15)～式(17)中Δl1i不等，得到：

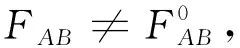
(18)

(19)

根据式(15)～式(17)得到：

(20)

(21)

分别将α12、α23、α34、ρ1、ρ4、θ、θ1、θ2、li1(i=1,2,3)、F输入等代入式(1)～式(21),并利用Matlab计算得出可移动折纸机器人的具体参数，见表2。

表2 折纸机器人参数

3.3 折纸机器人驱动部分设计及整体实验

机构的收缩状态如图10所示。

根据可移动折纸机构的运动几何特性，由式(1)和式(3)可知，通过改变θ即可控制折纸机构的折叠状态，而在其对称面Pi上，点n22、n24、n42、n4始终共线且相邻两点间的直线变换距离相同，这些点的运动规律恰好可由张拉整体结构中两杆张拉机构实现。因此，可通过控制两杆张拉整体结构的张拉特性来驱动折纸机构的折展运动，并用于可移动折纸机器人的设计，在CATIA软件中建立虚拟样机模型，得到机构的收缩状态见图10(a)。两杆张拉机构与折纸机构之间是通过将折纸机构从零厚度到厚板化后，将张拉整体结构驱动嵌入厚板折纸机构中，见图10(b)。

(a) 折纸机器人的折展

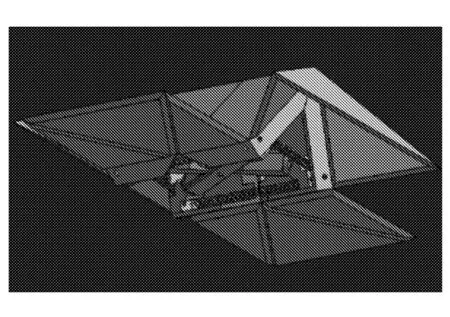
(b) 张拉整体结构嵌入式安装图10 机构的收缩状态

利用3D打印机打印出厚板构件，使用小铰链和两组拉簧完成折纸机器人的装配。完成样机实物模型的搭建,如图11所示。

(a) 机器人样机的平面展开

(b) 机器人样机的折叠图11 3D打印厚板折纸机器人

在折纸机器人机械结构的基础上，还需要加上驱动模块为机器人提供动力，驱动张拉整体结构形变，进而实现折纸机器人的折叠。

折纸机器人爬行如图12所示。

图12 折纸机器人爬行

折纸机器人包括一组张拉驱动单元、厚板化的折纸机构、类棘轮机构足和舵机。张拉整体结构驱动的可移动折纸机器人运动原理是在确定运动方向后，折纸机构完全展开时电机转动开始驱动，电机转动可以拉动绳索，绳索的另一端通过与特定折纸机构构件固定，带动张拉整体结构驱动拉簧收缩，进而减小张拉驱动机构运动方向上的长度，即实现折纸机构的折叠运动。又由于折纸机器人足部具有类棘轮机构，可实现折纸机器人运动。同理，在折纸机器人转向时，改变驱动电机即可。

4 结 语

基于折纸机构提出一种创新型双稳态单顶点五折痕折纸机构单元，通过机械结构设计制造可移动折纸机器人。张拉整体结构驱动的可移动折纸机器人具有两个主要特征：一是折纸机构方便运输和所占空间小等优点；二是具有张拉整体机构环境适应性强、稳定性好和机构刚度大的特点，通过主动改变折纸机构的输入角，可以实现稳定行走与转向。通过搭建物理样机，证明张拉驱动的折纸机器人能够稳定折叠与展开，并且可以在展开后实现转向功能，张拉整体机构拓宽了足式行走机构自适应性的研究。