基于灰色理论的私人汽车拥有量分析及预测
2021-10-16刘永超
邢 蕾, 刘永超
(长春工业大学 数学与统计学院, 吉林 长春 130012)
0 引 言
随着我国综合国力的日益强劲,人们的生活品质和物质水平得到显著改善。20世纪90年代之前,国内汽车市场大部分被地方政府以及企事业单位使用的公务车所占据,此外,企业的公共商务车也占有较大比例,只有相当少的私人用车;1990年以后的十年间,公务车的使用比例逐渐减少,商务用车比例日益上升,私人购车逐渐被更多人接受;2002年以来,私人购车已然成为我国汽车行业十分重要的一部分[1]。随着我国社会经济的日益增长,国民收入和生活水平得到改善和提升,购买汽车的能力大幅增强,与此同时,国家制定的一些相关政策也很好地推动了中国新能源汽车行业的繁荣和发展。
一方面,私人拥有汽车数量的多少与国民经济和社会发展是否健康高效、国内生产总值是否稳步提高、道路建设过程中是否安全有序具有密切联系;另一方面,私人汽车在国内的汽车生产和消费市场中已经处于举足轻重的位置,能够直接体现出整个国内汽车市场的发展状况,因此,私人汽车拥有量逐渐发展成为国内外专家学者们所需要和关注的研究对象。1967年,Mogridge M[2]首次利用英国家庭消费调查相关数据,基于家庭可支配收入和用于购买家庭使用汽车的消费支出,建立了汽车拥有量的预测模型;2002年,Soligo K[3]建立了经济发展与私人汽车拥有量之间关系的模型,并且证明了该模型足够通用到其他消耗燃料,如家用电器等方面;Joyce M Dargay[4]使用伪面板方法研究英国农村和城市家庭汽车拥有量的因素, 结果显示,汽车运输成本的增加会对农村家庭造成更大的经济负担,针对不同地区给出具体的运输措施;2004年,Hong S K等[5]针对1995年NPTS的数据建立有序Logit模型进行分析和评估,结果表明,改善公共交通可以增加汽车的使用;Anowar S等[6]应用潜在有序Logit模型和无序多项式Logit模型,并用加拿大魁北克市的数据进行估算,验证了这些模型在汽车拥有量决策方面的优势,无序选择机制的表现略好于有序响应机制;2010年,Nolan A[7]利用爱尔兰一项生活调查的纵向数据来分析估计家庭汽车拥有量的动态随机效应概率单位模型,结果显示,收入是家庭汽车拥有量差异的最强决定性因素;2016年,Wu N等[8]采用固定效应模型和随机效应模型对32个省会城市的私家车拥有量相关数据估计结果进行了研究比较,结果显示,固定效应模型的性能要明显优于文中提到的另外两种模型。
随着中国的稳步发展,汽车私有数量的持续增加,国内研究学者也进行了很多相关研究。韩雪等[9]引入与私人汽车拥有量相关的解释变量,建立线性回归模型,较为精准地得到了私人拥有汽车数量的短期预测结果。随后很多学者选择使用线性回归这一简单实现且容易理解的模型进行分析与预测,主要区别在于解释变量的选择上有所不同[10-12]。由于灰色系统模型不必明确数据分布,而且对研究数据没有十分苛刻的制约,应用较方便,很多学者以此展开了大量工作。朱开永等[13]根据灰色理论,以私家车保有量数据建立预测模型,并利用灰色关联分析法得到了影响私家车保有量的主要因素;刘利斌等[14]运用灰色理论和线性回归思想针对特定地域的数据,建立了私人汽车保有量的预测模型,得到比前者更好的预测结果;洪求枝等[15]以灰色系统比作私人汽车拥有数量的变化过程,建立了GM(1,1)模型,将其应用于实际数据上,并进一步验证了该预测模型的可行性[16];李乃伟等[17]利用灰色理论建立GM(1,1)动态预测模型,根据精度大于90%的要求提出10种预测模型,得到了较准确的预测结果,为城市交通规划等各方面的研究提供了依据;斯琴[18]利用GM(1,1)及其修正模型对私人拥有汽车的数量数据进行预测,证明了后者的预测精度比前者更好,在短期的预测精度方面也比前者更加理想。
这些研究工作在对汽车拥有量数据分析和预测等应用方面已经取得了一定的进展,多元线性回归模型的建模及预测过程容易实现、结果具有很好的可解释性,但在一定程度上可能忽略了交互效应和非线性的因果关系,导致预测结果不够准确。灰色预测模型对研究数据没有严格要求,并且模型的预测精度相对令人满意,可适用于短期、中长期预测。文中利用自适应Lasso估计方法进行变量选择得到影响我国私人汽车拥有量的主要因素,建立灰色GM(1,1)模型对其进行分析预测,最后,根据相对误差等统计指标比较不同模型的预测结果,为国家和汽车行业制定相关政策提供理论支持。
1 灰色GM(1,1)模型
灰色预测模型是对单个时间序列进行建模和预测的一种方法,它对所研究的数据没有严苛的制约,以不完全知道样本信息的小样本为主要研究对象,不需要明确原始数据属于何种分布,建模精度具有一定的优势,被普遍应用在经济等领域。灰色GM(1,1)模型是所有灰色预测理论中的一个基础理论模型,也是所有灰色理论中应用最为普遍的一种灰色预测模型,适合对数据量少以及信息不足的序列进行中短期的灰色预测,在这种灰色预测系统中,由于所能获取的序列信息往往是有限的,因此常常需要对序列做一些处理,减弱序列的随机性,经常被用到实际中的处理办法主要有:累加生成、累减生成和加权邻值生成,文中选择的是累加生成方法[19]。
灰色预测模型的建模步骤为:
已知原始序列
X(0)={x(0)(1),x(0)(2),…,x(0)(n)}
有n个非负观测值,对该序列进行累加生成变换,得到
X(1)={x(1)(1),x(1)(2),…,x(1)(n)},
其中
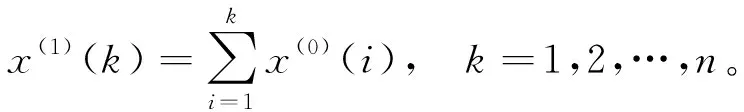
(1)
计算紧邻均值序列
Z(1)={z(1)(2),z(1)(3),…,z(1)(n)},
其中
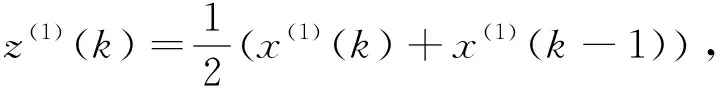
(2)
则得到一阶单变量的灰色GM(1,1)预测模型形式为
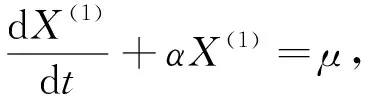
(3)
式中:α----发展灰数;
μ----内生控制灰数。
令θ=(α,μ)T为待估参数,利用最小二乘法进行求解,解得
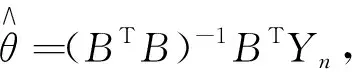
(4)
其中
Yn=(x(0)(2),x(0)(3),…,x(0)(n))T,


(5)
将预测累加值还原为预测值
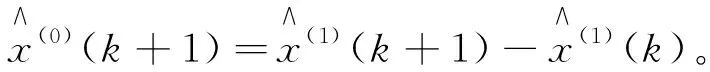
(6)
为了保证所建立的模型能够拥有较高的精度应用于实例的预测中,通常需要经过残差检验、关联度检验以及后验差检验。若序列残差满足Δk<10%,则表示灰色GM(1,1)模型的预测精度较高;若关联度r>0.6时,可以认为GM(1,1)模型的预测结果较好;若后验差满足C<0.35,则说明灰色GM(1,1)模型的预测效果是令人满意的。
2 实证分析
2.1 数据来源
根据《中国统计年鉴》2000—2019年共20年我国私人汽车拥有量的相关数据,选取了7个相关解释变量见表1。

表1 2000—2019年私人汽车拥有量及相关数据

续表1
应用自适应Lasso估计方法对这7个解释变量进行变量选择,进而得出对私人汽车拥有数量产生影响效应的主要变量,利用灰色理论进行预测,比较不同方法的预测效果。
2.2 基于灰色GM(1,1)模型的实证分析
中国私人汽车拥有量与时间的关系如图1所示。
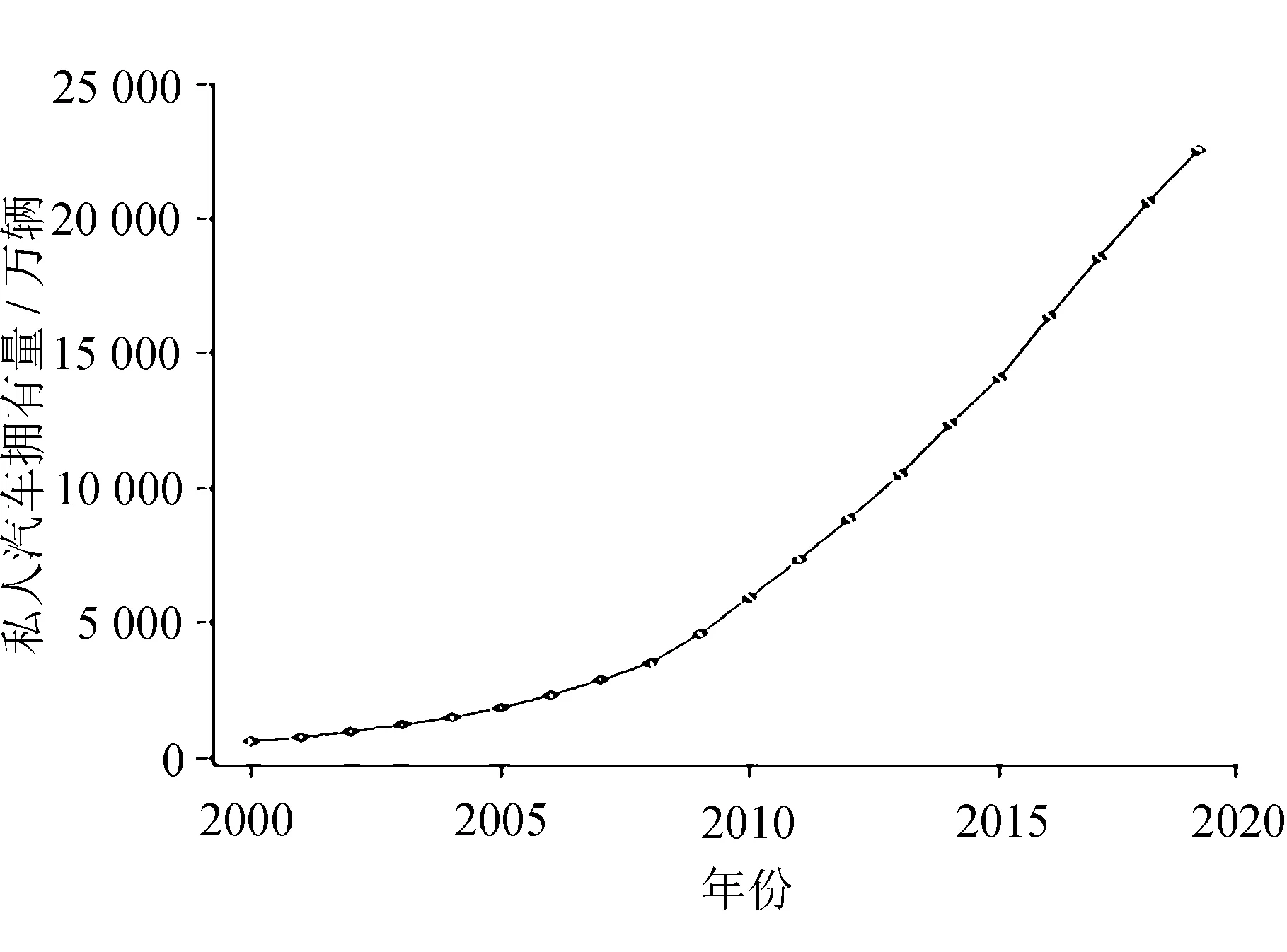
图1 中国私人汽车拥有量与时间的关系
由图1可以看出,2000年以来,中国私人汽车拥有量一直呈现递增的趋势,利用灰色理论和模型构建过程以及表1中的私人汽车拥有量的数据,在R语言的基础上进行建模,由于在实际灰色理论建模中,原始时间序列不一定都被用来进行建模,通过建立不同维数的序列可以得到不同的参数和预测值,因此,通过筛选适当的维数可以得到预测精度最高的GM(1,1)动态预测模型,模型通过一系列检验后,相对误差不超过1%,预测结果见表2。

表2 GM(1,1)模型检验及预测
计算关联度
r=1.137 334>0.6,
该值说明所建立的模型关联性较好,后验差比值
说明所建立模型预测的很好。
2.3 基于自适应Lasso估计方法进行变量选择
Lasso估计方法是通过在回归模型中加入惩罚项,实现了在多个解释变量中快捷地选择其中较为重要变量的一种有偏估计方法,而且自适应Lasso估计方法在对变量的选择方面要比Lasso估计方法更加适合,在实际应用中有更好的表现[20]。
变量间的相关系数见表3。
表3中,解释变量x1、x2、x3,x4与y的相关系数分别为0.944 8、0.989 9、0.997 2、0.936 7,说明这4个解释变量与y有非常强的正相关关系;解释变量x6和x7与y的相关系数分别为0.894 3和0.830 2,说明这两个解释变量与y有比较强的正相关关系,而解释变量x5与y的相关系数为-0.333 2,该解释变量对y的影响较小。

表3 变量间的相关系数
根据Pearson相关系数检验结果,可以初步认为选择的7个解释变量对我国私人汽车拥有量都存在一定的相关关系,利用自适应Lasso估计方法对解释变量进行选择,得到回归方程
yt=-0.619 3x2t+1.615 9x3t+0.026 2x4t+et,
et=0.233 6et-1-0.058 4et-2+0.071 1et-3+σεt。
(7)
由式(7)可以清楚的看出,我国私人汽车拥有量与国内生产总值(亿元)、居民消费水平(元)、全国汽车产量(万辆)之间具有较强的相关性,与年末总人口数(万人)、燃料动力类购进价格指数、钢材产量(万t)和公路里程(万km)之间的相关性比较弱,其中居民消费水平(元)的影响最大。
利用自适应Lasso估计方法选择的变量建立多元线性回归模型并预测,这里只列举了2015—2019年我国私人汽车拥有量的预测结果,相对误差都在2%之内,模型拟合较好。
基于Lasso的线性回归模型检验及预测见表4。
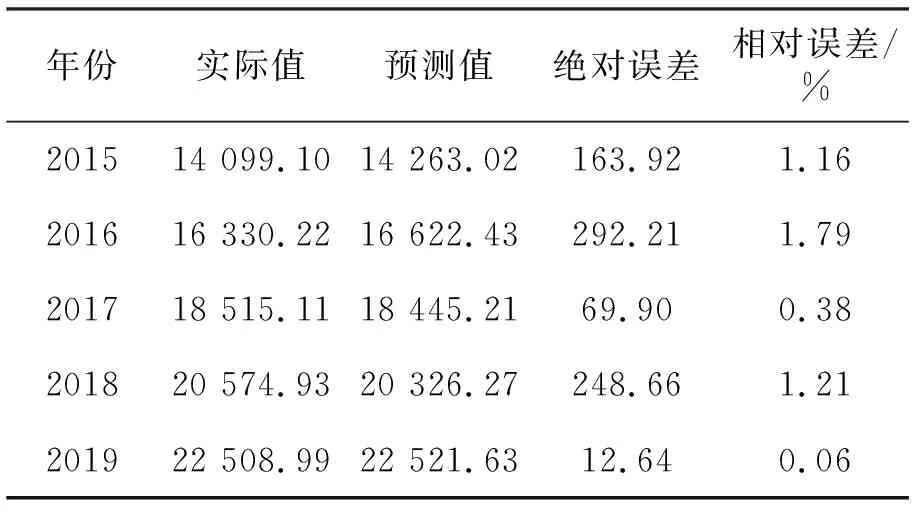
表4 基于Lasso的线性回归模型检验及预测
利用逐步回归得到回归模型,即
y=-0.031 4x1-0.029 2x2+1.975 0x3+
0.486 5x4。
(8)
模型的R2=0.999 8,模型对应的P值小于2.2×10-16,模型拟合的很好。
将表1中的数据代入式(8),得到逐步回归模型检验及预测结果见表5。
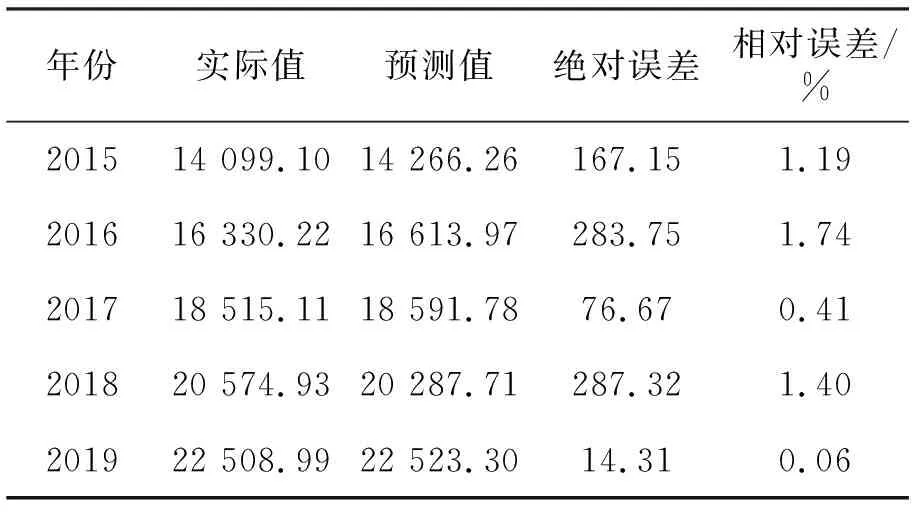
表5 逐步回归模型检验及预测
由表5可以看出,显然逐步回归模型预测结果的绝对误差要大一些,自适应Lasso估计方法进行变量选择为多元线性回归模型的预测提供了一种更好的方法。
利用灰色理论预测出2017—2019年各因素的数据见表6。

表6 2017—2019年各因素的预测值
将表6中的数据代入式(8),得到私人汽车拥有量分别是18 468.49万辆、20 710.59万辆和22 501.15万辆,对应的相对误差分别是0.25%、0.66%和0.03%,该方法得到了更好的预测结果。
通过以上分析结果易知,普通线性回归和基于自适应Lasso变量选择后的回归对20年数据进行预测,相对误差基本相同且大多数在2%之内,但自适应Lasso估计方法缩减了逐步回归的时间和过程,为建立回归模型进行预测提供了一种易于实现和理解的途径和办法,而对三维私人拥有的汽车数量短序列建立的GM(1,1)模型,得到的预测精度最高,相对误差在1%之内,也间接说明了灰色模型更多地适用于对包括不确定信息进行短期预测。
通过上述检验证实了所建立的GM(1,1)预测模型是可行且有效的。利用建立的这个模型对我国未来两年的私人汽车拥有量数据进行预测,结果如下:
2020年,我国私人汽车拥有数量

2021年,我国私人汽车拥有数量

3 结论与建议
1)运用自适应Lasso估计方法实现变量选择,在已有的7个解释变量中,年末总人口数(万人)、燃料动力类购进价格指数、钢材产量(万t)和公路里程(万km)不是直接影响我国私人汽车拥有量的主要因素;
2)通过使用不同维数的私人汽车拥有量短序列建立GM(1,1)动态预测模型,以预测精度最高的模型来预测出2020年和2021年我国私人汽车拥有量数据分别是24 604.58万辆和26 915.8万辆,根据预测结果,该方法在短期预测方面更有效且精度更高,可以应用到小数据、贫信息方面;
3)虽然考虑了经济等因素与私人汽车拥有量的关系,但因为数据会受到多方面影响因素的制约,存在着一定趋势的同时具有随机性,相关的预测模型很难得到非常准确的长期预测结果。
私人汽车数量日益增多不是单一因素导致的结果,而是经济因素、人口密度、道路面积等多方面因素共同形成的现象[21]。在回归方程中,居民消费水平(元)对应的系数为1.615 9,对我国私人汽车拥有量产生了最大的影响效应,因此对于国家来说,增加居民收入、提高居民的消费水平是增加私人拥有汽车数量的重要举措之一,只有当个人存有充足的资金后,才能将其用于汽车这类消费品上,才会有愈来愈多的人注意到汽车市场,购买私人使用的汽车;其次,全国汽车产量(万辆)对应的系数为0.026 2,对私人汽车拥有量有微弱的影响效应,汽车制造及相关行业应在增加汽车数量的同时,对现有汽车进行技术创新,制造更适合家庭使用的汽车,增加私人汽车拥有量的数量同时使得汽车行业合理、高速的发展。
