桩间土拱空间演变机理与构造柱支护应用研究
2021-10-15黄俊文刘笑含夏力农
黄俊文 刘笑含 廖 飞 夏力农
1.中建五局第三建设有限公司 湖南 长沙 410004;2.长沙学院 土木系 湖南 长沙 410003
一般认为,当排桩间距布置满足一定要求时,基坑开挖过程中引起的推力荷载将通过土体应力重分布最终由桩来承担,其主要原因是土体在邻近排桩的区域形成了土拱效应。
该现象最初由Terzaghi提出,并采用活动门试验对其进行验证。Liang等[1]对土拱效应产生的机理进行了系统分析。卢廷浩[2]通过力学概念对土拱效应进行了理论分析,得出了合理桩间距的确定方法等。冯君等[3]从方桩桩间土拱形成的机理、力学特性入手,建立了最大桩间距计算模型并进行验证。贾海莉等[4]基于土体的极限平衡条件对滑坡推力作用下的土体中的成拱作用进行研究,得出了抗滑桩的最大桩间距公式,并给出了在考虑土拱效应的情况下合理桩间距的确定方法。赵明华等[5]建立出相应的双土拱简化计算模型,并基于摩尔-库仑破坏准则及极限平衡理论,推导出抗滑桩合理桩间距计算公式。杨明辉等[6]分析了双排抗滑桩结构承载的最不利状态,利用土拱抛物线拱轴线的几何特征及拱脚处的力平衡及应力状态,导出作用于双排桩桩侧的坡体土压力分布。周应华等[7]从推力桩桩间土拱形成的机理和力学特性入手,根据桩间土拱的静力平衡以及拱脚处土体本身的强度条件,建立了相应的计算模型。王军等[8]、王洪木等[9]、商秋婷等[10]采用有限元方法对土拱效应进行了二维、三维分析,探讨了土拱效应与桩径、桩间距等参数之间的关系。胡敏云[11]、耿建勋等[12]归纳了合理桩间距计算式,结合工程实例进行了分析,从综合效益等方面得出了一些有益结论。
综上所述,对土拱效应的研究已取得较全面的成果,但仍存在以下不足:未考虑土拱的演变情况;桩间小土拱和大土拱拱形均为合理拱轴线,与实际工程中有一定的差异;假定土拱拱厚等于方桩抗弯一侧的宽度或圆桩内接正方形的边长缺乏理论依据。
针对上述不足,在已有理论研究基础上,本文采用有限元方法分析了不同土体性质及自重荷载对土拱演变的影响,并结合桩间土垮塌实例,首次提出、开展了桩间土构造柱加固措施并应用于工程实际,取得了良好的效果。
1 计算原理及参数
1.1 计算原理
模型中土层选择可以模拟土体弹塑性特点的摩尔-库仑模型,支护结构采用线弹性模型。单元类型均为八结点线性六面体单元C3D8R。为简化计算,有限元计算模型中的土层假定为水平分布、均匀、连续及各向同性。
考虑模型的对称性,取1/2部分进行分析。模型土体表面水平,计算区域竖直方向取14 m(2倍基坑深度),纵向取8 m(同钢支撑间距),横向取16 m,支护桩直径0.8 m、桩间距1.5 m、桩长10 m,基坑深度7 m,钢支撑直径0.6 m。模型顶部为自由边界,四周采用水平方向约束,模型底部为固支约束。支护结构-土界面建立库仑摩擦模型的接触关系,采用主-从(master-slave)接触算法。有限元计算简图如图1所示。
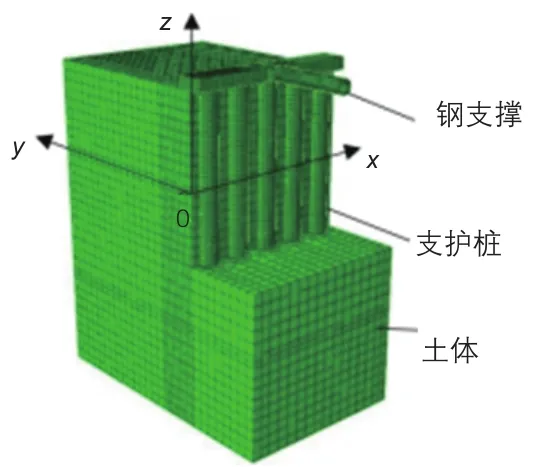
图1 有限元计算示意
1.2 计算参数
混凝土参数按GB 50010—2010《混凝土结构设计规范》选取,弹性模量取3.00×104MPa;钢支撑弹性模量取210 GPa。岩土的力学参数见表1。
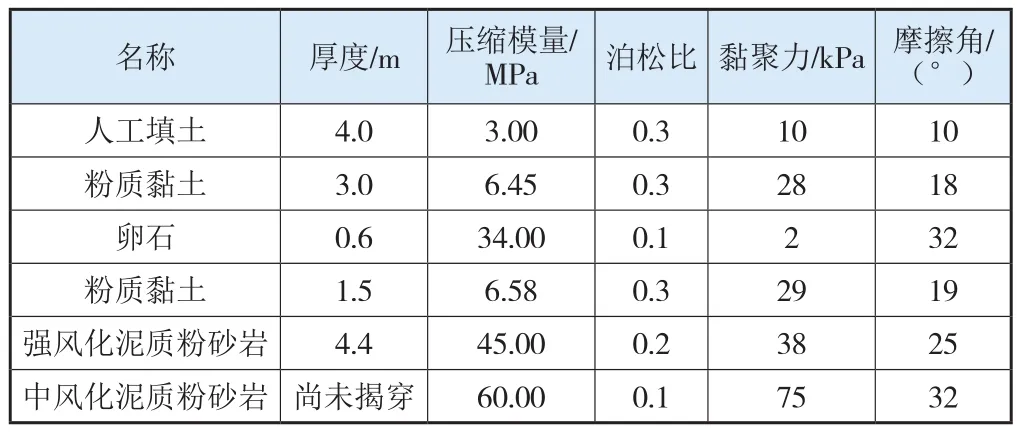
表1 岩土主要物理力学参数
2 模拟结果
支护桩之间的土体在土压力作用下必有向前挤出的趋势。由于土体固有物理特性,导致土体能在一定桩间距条件下形成以相邻两侧桩为拱脚的土拱。而应力重分布与土拱的形成情况密切相关,当桩间土颗粒受挤压作用时,应力必然改向,倾向于横向分布,这种倾向是形成土拱效应的重要原因。因此,可以研究最不利部位跨中x向水平应力、应变等的变化趋势,分析土拱演变情况。
2.1 最不利部位
图2为桩周土位移分布云图。可以看出,在自重荷载作用下,桩周土体的位移最大值正好位于人工填土层与粉质黏土层的交界面,并向上、下部土体以逐渐削弱的趋势扩散。为进一步探索桩周土变形情况,将基坑周边土体不同深度h处的水平位移sH进行统计(图3),可知基坑侧壁土体的水平位移明显较大,峰值区域在4 m附近,桩间土有向前挤出的趋势,且变形的峰值区域随着距离的增加而呈上移趋势,不过随着距离的增大,水平位移逐渐减小。因此,基坑深度4 m部位为该工况下最不利部位,可作为进一步研究方向。
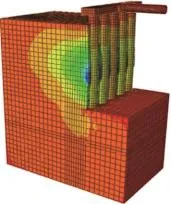
图2 位移云图
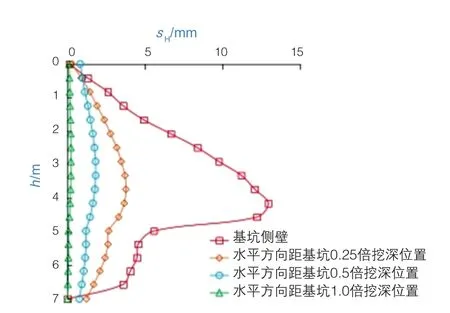
图3 桩周土水平位移示意
2.2 土拱的空间效应
图4为4 m部位桩间土等效塑性变形云图,可知塑性发展区域主要集中在人工填土底部,整体呈扇形扩散趋势,表明该工况下,在一定高度范围内自上而下均有土拱形成,且证明土拱是一种空间效应。图5给出了最不利部位主应力分布图,由图5可知:土体应力会出现沿x向迁移现象。桩周局部范围内,靠近临空面的主应力方向迹线呈坦拱形态,其他部位呈陡拱形态。表明荷载是以拱的形式转移到固定的支护结构上,土体中沿最大主应力方向的迹线就是土拱轴线。
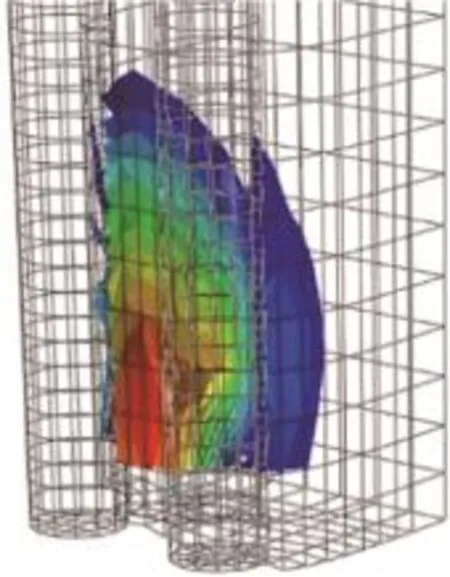
图4 等效塑性变形云图
文献[4]认为,水平土拱可分为3个区域,即:拱后稳定区、土拱区及拱前自由区,且土拱区的大小土拱是重合的。该结论的得出是基于假定大小土拱拱跨相同、土的性质一定、拱形总是合理拱轴线。在桩径0.8 m、桩间距1.5 m的情况下,忽略桩径对大小土拱的拱跨影响显然是不合理的,因此土拱区的大小土拱不能认为是完全重合的。从图5还可以看出,主应力方向在桩间小范围内存在坦拱与陡拱的清晰界限。若仅存在唯一土拱,则在稳定土拱作用下的桩间土临空侧应无拱后推力作用,拱前自由区作为独立土柱而自立。因此,假定土拱拱形总是合理拱轴线也缺乏依据,桩间存在大小土拱的协同作用。图6为有限元分析得出的土拱分区示意,土拱可分为4个区域,即拱后稳定区、大土拱、小土拱及拱前自由区。

图5 主应力分布云图
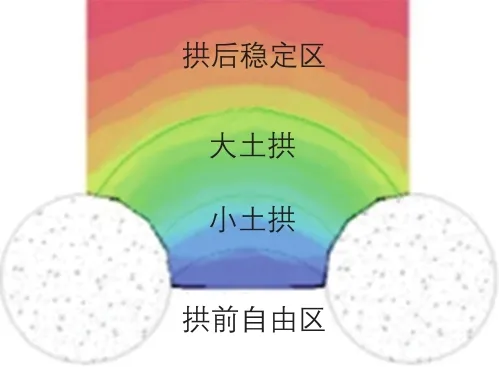
图6 土拱分区示意
2.3 土体性质对土拱演变的影响
黏聚力和内摩擦角变化在一定程度上反映了地下水使土体的软化程度。分析结果表明,在相同荷载作用下,不同的黏聚力、内摩擦角对土拱演变有明显影响。
图7为黏聚力c分别为5~10 kPa时的水平方向应力σx对比图。由图7可知,黏聚力变化对应力重分布有较大影响,且均会出现应力集中和应力释放现象。黏聚力越大,应力集中越明显,集中区间越靠前,说明土拱矢跨比随黏聚力的增大而变小。为进一步了解应力集中区域迁移情况,图8给出了水平方向应力σx峰值部位随黏聚力变化曲线,发现当黏聚力增大时,σx峰值部位整体呈前移的趋势;但当黏聚力为7~8 kPa时,峰值部位无明显变化。主要原因在于,通常以抗剪强度作为土的强度,随着黏聚力不断增加,桩间土的抗剪强度增大,桩-土相对水平位移减小,因而土拱效应逐渐削弱。而峰值曲线存在稳定区(7~8 kPa),但应力集中区域随黏聚力增大而变小的现象表明当土拱稳定时,土拱拱厚随黏聚力的增大而变小。

图7 σx-dy计算曲线
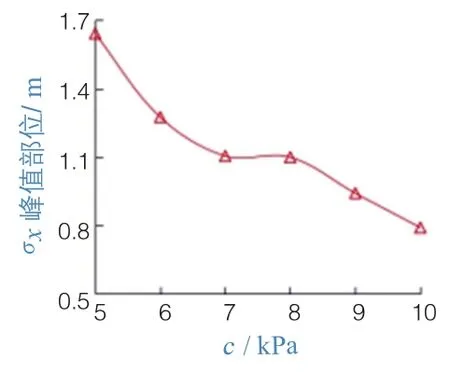
图8 σx峰值部位-c变化曲线
图9为摩擦角-水平方向应力计算曲线。可以看出应力集中和应力释放现象是比较明显的。摩擦角在20°~30°区间段内,σx调整范围不大,且应力集中区域相对靠前;摩擦角在15°~20°区间段内,σx变化幅度相对较大,应力集中区域明显扩张;摩擦角在10°~15°区间段内,σx变化幅度显著增加,应力集中区域明显后移。偏于安全原因,取土体的等值内摩擦角φE等于土体的内摩擦角φ,则可知桩侧静摩擦因数f=tanφ,即随摩擦角变小,桩-土界面的摩擦力逐步削弱,此时拱脚支撑将更依赖于桩的强度,且抗剪强度与土的内摩擦角也是呈正比关系的。图10给出了σx峰值部位随摩擦角变化曲线,结果发现峰值部位随摩擦角增大而前移,但摩擦角为15°~20°及25°~30°时,峰值部位趋于平缓。表明土拱拱圈在这两个阶段是稳定的,而应力集中区间扩张表明土拱拱厚会随摩擦角的变化而调整,即拱后稳定区土体会由于摩擦角变小而参与土拱受力。

图9 φ-σx计算曲线
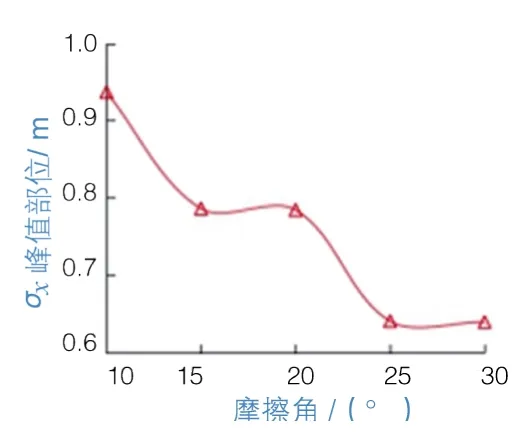
图10 σx峰值部位-φ变化曲线
2.4 不同荷载作用下土拱的演变
由结构力学,土拱拱圈应逐步使得各个截面均不出现拉应力,其压力线不应超出截面核心,并逐步靠近合理拱轴线。但是剪切破坏是土体破坏的重要特点,当拱体剪切应力小于土体抗剪强度时才可能调整自身强度抵抗外力,因此,荷载在一定程度上也将直接影响桩间土的成拱现象。通过对人工填土层施加10、12、14、16、18、20 kPa的自重荷载,分别计算最不利部位的σx及等效塑性应变分布情况。
分析发现,当自重荷载L增加时,土拱效应作用区域内应力集中现象逐步增强,且集中区域整体后移(图11)。从应力峰值部位曲线(图12)可以看出,自重荷载增加会引起应力峰值部位增大。主要原因在于,随着σx不断增加,桩间土水平位移增大,桩-土相互作用已不能满足拱脚的稳定,桩间小土拱逐步失效,大土拱则由于拱后递增推力及连拱效应的影响,主拱圈均会往拱后稳定区移动。此时,拱脚的稳定主要取决于支护结构迎土侧土体强度。但由于合理拱轴线的存在,应力峰值部位会存在平缓区,而应力峰值部位在自重荷载为12~14 kPa及18~20 kPa共2个阶段相对稳定。表明自重荷载为14 kPa时已达到第一个阶段的土拱稳定临界状态。同时,土体也会由于应力重分布而再次接近新的合理拱轴线。

图11 L-σx计算曲线
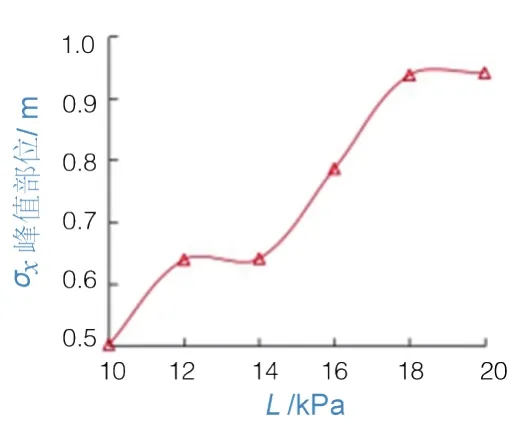
图12 L-σx峰值部位变化曲线
如前所述,随着自重荷载的递增,土体有效应力增加,土拱存在“成拱—稳定—失效—再成拱”的演变过程。目前尚无可靠手段直接探测到土拱失效后再稳定现象的客观存在。但可以肯定的是,土拱失效是桩间土体内应力屈服的一种表现形式。由图13可以看出,等效塑性应变εep区间随自重荷载增加而增大,说明在桩间土成拱过程中,主拱圈土体颗粒会通过塑性应变的方式重新排列。由图14可知,εep峰值部位随荷载增加而从拱前自由区前端往小土拱区域移动,但自重荷载为12~18 kPa阶段相对稳定。表明过大的自重荷载会造成土拱破坏,且第一阶段土拱失效至第二阶段成拱过程中,桩间土破坏面主要集中在小土拱区域。而应力峰值会在14~18 kPa阶段明显后移(图14),表明在此阶段主拱圈后移而破坏面不变,桩间会再次形成新的小土拱区域。
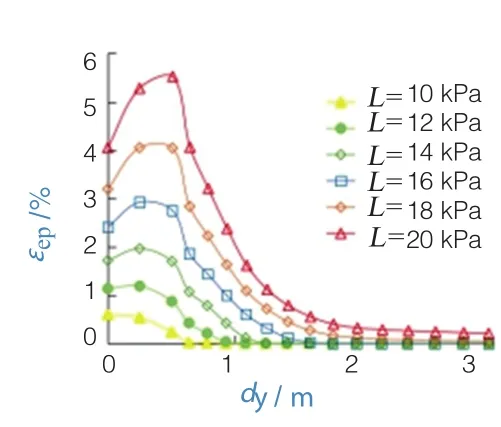
图13 L-εep计算曲线
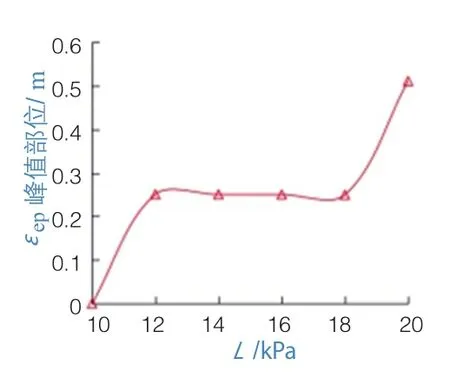
图14 L-εep峰值部位变化曲线
3 桩间土垮塌实例
因受用地限制,长沙市老城区湘府西路综合管廊工程采用排桩支护,无回槽形式开挖,即单边支模。考虑避让既有错综复杂的地埋管网,相邻两桩设计间距偏大,此时,桩间土的稳定性成为了基坑支护设计的关键因素。施工过程中部分区域土体垮塌,对已垮塌区域进行分析可以得出如下结论:
1)地质条件与桩间土成拱与失效密切相关。相对软弱稳定性差的地层,拱前自由区垮塌现象较为严重。粉质黏土层、强/中风化岩层自稳性较好,即使采用敞开模式开挖,也未出现桩间土垮塌现象。表明在土质较好的情况下,稳定土拱的矢跨比较小。这与前文研究的土体性质对土拱演变的影响得出的结论是一致的。
2)桩间土会由于基坑开挖而逐步垮塌释放应力,并呈现新的土拱形态。在局部软弱土区域,若未及时针对该土拱采取加固措施,建立有效的土压平衡,则会出现类似连拱效应的坍塌情况,表明实际工程中土拱存在演变过程,但在土体性质较差的情况下,未采取任何加固措施则不存在稳定的土拱。
3)在地下水富集、水压力比较大的地段,由于基坑开挖及降排水,孔隙水压力消散,在渗流力作用下形成管涌现象,桩间土整体失稳,未见稳定的土拱。
4 桩间土构造柱研究
根据现场实际情况及土拱空间演变机理,本工程首次提出桩间土设构造柱稳定措施(图15)。其作用机理如下:沿冠梁在拱前自由区顶部预埋套管,由支护桩净距0.7 m可推断拱前自由区与支护结构存在咬合力,在桩间增设φ800 mm高压旋喷桩可达到加强咬合结构的作用。同时,旋喷桩能够提高土体的黏聚力及内摩擦角,使得应力峰值部位前移,达到缩小拱前自由区域的目的。因此,在土层软硬交界面位置设置φ1 m的实桩可起到支座作用,冠梁作为另一端支座,注浆完成后立即安放构造钢筋,本工程实践中采用单支φ16 mm纵筋。
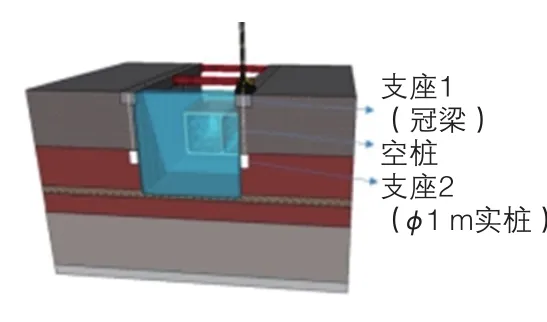
图15 桩间土构造柱
该技术无需采用新型的施工设备,对既有管线的扰动极小,保障了桩间土及地埋管网的安全,改善了作业环境,提高了工效,降低了成本。与国内外现行桩间土稳定技术相比,具有主动控制的优势,解决了地下管网错综复杂情况下的排桩支护结构适应性问题。
4.1 数值模拟
土拱效应存在明显的三维特征,为研究简便,将其简化为单位厚度水平土层上的平面应变问题(图16)。其中土体采用人工填土参数、桩间土构造柱采用混凝土参数。假定桩体和构造柱的侧向位移为0,采用固支约束,而土体两侧采用水平约束,顶部为自由端。不失一般性,假定桩后土压力均为水平方向,计算时在模型顶部分别施加10 kPa均布荷载。同时,为了避免边界效应影响,土体横向宽度大于基坑深度取8 m。
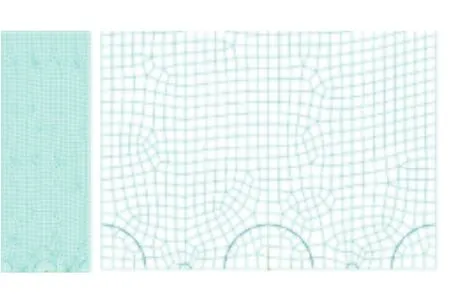
图16 有限元计算示意
4.2 模拟结果
从图17可以看出,大主应力的方向在排桩附近产生水平迁移现象,表明桩间构造柱不会消除土拱效应,对桩间土的安全性起主控作用的依旧是土拱的稳定性。从水平应力云图明显可以看出,在桩间构造柱的影响下,拱脚支撑点会往前移,这就导致拱跨变小,连拱效应削弱,且拱脚处的受力方向与支护结构夹角越接近90°,如此,拱脚的水平推力主要依靠排桩的刚度来平衡,对桩-土摩擦力依赖性较小。上述研究表明,桩间土构造柱措施不仅对拱前自由区的稳定性有利,且能够分担土拱的荷载,改善土拱受荷工况。

图17 大主应力分布与水平应力云图
图18为土体Mises应力分布及云图,可以看出排桩及桩间构造柱正上方均出现了应力集中现象。表明桩间构造柱能够限制应力绕流现象,这有利于加强桩后土体的楔紧效应和减小拱前自由区的拱后推力,须知楔紧的过程类似于土质改良的过程。而前文的研究表明,土质越好,土拱演变越处于初始阶段,拱越靠前,这进一步解释了拱脚前移的原因。值得注意的是,此时的土拱矢跨比并不一定呈减小的状态,说明桩间构造柱并不会消除土拱效应,但会影响土拱的成拱形态。若要得到其普遍规律需做进一步研究。
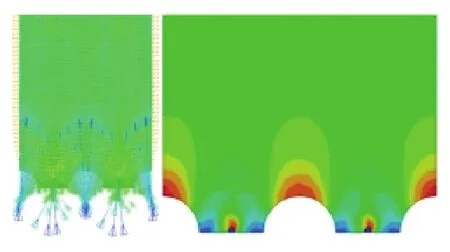
图18 Mises应力分布及云图
5 结语
以长沙地下综合管廊湘府西路支护工程实例为基础,运用有限元方法对分阶段成拱效应进行模拟,得到以下几个结论:
1)土拱效应是一种空间效应。在相对软弱的土层中,土拱效应沿高度方向呈下强上弱的趋势增长。水平土拱分区可以分为拱后稳定区、大土拱区、小土拱区以及拱前自由区。
2)黏聚力、内摩擦角、荷载均对土拱演变有较大影响。土拱矢跨比和拱厚均随黏聚力或内摩擦角的增大而变小,随荷载的递增而增大。
3)随着参数的变化,土拱存在“成拱—稳定—失效—再成拱”的演变过程。第一阶段土拱支撑依赖于桩-土作用,第二阶段的土拱主要靠连拱效应稳定。
4)桩间土构造柱加固措施不仅对拱前自由区的稳定性有利,且能够分担土拱的荷载、限制应力绕流现象、加强桩后土体的楔紧效应和减小拱前自由区的拱后推力,改善土拱受荷工况。
