超高可靠性低时延通信的资源优化分配研究

马晓莹，王志欣通信作者，卢忠青

（1.国家无线电监测中心，北京 100037；2.深圳大学，广东 深圳 518000）

0 引言

超高可靠性低时延通信（URLLC）是3GPP组织提出的下一代移动通信场景中的三大场景之一，该场景旨在为各种时间敏感应用（如工厂自动化、自动驾驶）提供超低的时延保证以及超高可靠性保证。URLLC对时延以及可靠性的超高要求对下一代移动通信的设计带来了严格的要求，在如此高的可靠性要求以及无线链路的高衰落的情况下，仅使用单次传输是非常不经济的，3GPP组织建议使用多次传输来实现通信的超高可靠性。文献[1]研究了相似场景中的上行传输部分，通过采用重复传输来缩短传输时延和提高传输的可靠性。受其启发，本文研究了重复传输方式下物联网场景中下行链路的超高可靠性实现。

1 传输模型

1.1 可靠性

传输模型如图1所示，图中A表示基站，B表示无线信道，C表示数据包接收端。由于本文采用重复传输实现通信的超高可靠性要求，即B、C处的传输可看作多条路径。数据包成功传输的前提是A、B、C三处的传输均不出现错误。依据URLLC中对通信服务质量（QoS）的定义，下行用户面时延包含两个部分：基站处的排队时延Dq；据包处理时延Dproc=0.1ms。本文将数据包下行链路的用户面时延Dmax设为0.5ms，则Dq≤0.3ms。数据传输可靠性εmin为1-10-5。本文假设基站处数据包的排队时延不超过Dqmax=0.3ms的概率为PA，假设数据包的第k条路径中B处传输成功的概率为PBk，C处解码成功的概率为PCk，则数据包成功传输的概率为PS为：

图1 传输模型图

1.2 有效带宽

有效带宽是评估排队系统以满足实时服务的统计设计需求的有力工具[2]，[3]，[4]。文献[5]验证了URLLC场景中利用有效带宽评估基站处的排队时延违反概率的有效性，因此，本文中采用有效带宽来对基站处的排队进行建模。

本文假设模型中基站处传感器的数据包到达过程是均值为λ=λab（单位：packet/s）的泊松达到过程。依据有效带宽的定义，基站处的有效带宽为：

式中，λ=λab，b是数据包大小。

假设n时刻达到基站的数据包经历的排队时延为Q（n），最大容忍时延为Dq，基站处的服务速率为r，依据上文中的推导，则

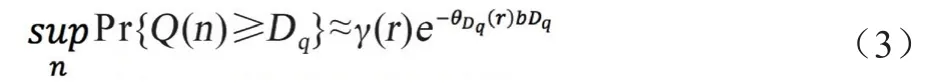
式中，γ（r）是队列长度非空的概率；θ是QoS的表征参量。可以看出，当越大，排队时延违反概率越小，且满足时，本文对基站处的排队稳定性的评估仍然是有效的。

1.3 主动丢包和解码错误概率

依据文献[6]，短帧传输下的信道容量R可记为：

式中，u表示大尺度信道衰落；g表示小尺度信道衰落；σ2表示信道噪声功率谱密度；Tf表示一个帧的时间长度；PCk表示接收端的解码错误概率；fQ-1（x）是高斯Q函数的反函数；V表示信道色散。

因此，对于恒定的信道容量，解码错误概率越低，单次传输对信道质量的要求越高，对传输功率的要求也越高。当瞬时信道增益g的值过分小（信道处于深度衰落）时，为维持信道容量需要消耗大量的传输功率，因此，本文将直接舍去该次传输。由于舍弃传输导致的传输失败即对应传输失败概率1-PBk，则

1.4 最小化重复传输功率模型

在重复传输策略下，以最小化重复传输功率为目标，本文提出以下最优化问题模型：

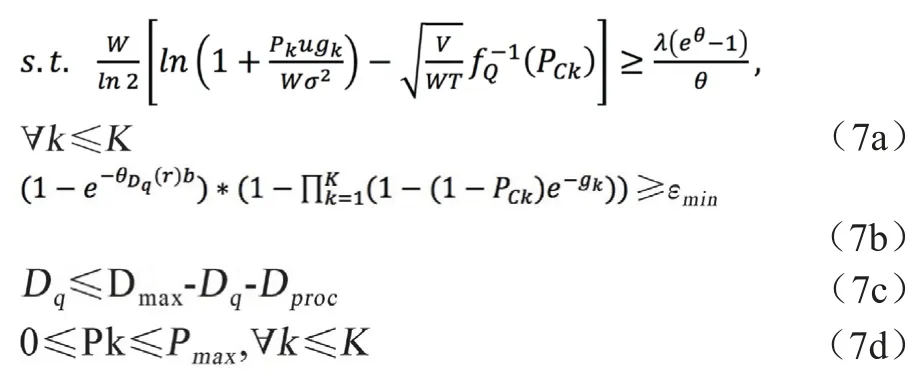
其中，约束条件（7a）表示单次传输的信道容量应不小于基站处泊松达到过程的有效带宽，保证了本文对基站处排队时延的评估的有效性；约束条件（7b）表示系统的可靠性应不小于99.999%。

2 模型求解

该模型是一个混合整数非线性规划问题，不易直接求解，式中K的取值通常在10以下，因此可以通过单独求解K取1到10时目标函数的最优值，而后再进一步优化K的取值。

2.1 K=1

当K取1时，意味着系统只进行单次传输。假设系统的吞吐量足够高，PA≈1。约束条件（7b）同样是两个小于1的数的乘积，因此，（1-PC）和e-g都应大于99.999%。令e-g=99.999%，则g≈10-5，此时信道处于深度衰落中，需要消耗巨大的传输功率方能满传输可靠性要求。因此，当K=1时，该问题在可行域内不存在最优值，也即无法通过单次传输达到URLLC的可靠性要求。

2.2 K>1

为了方便分析，令K取5时，且约束条件（7b）取等号时：

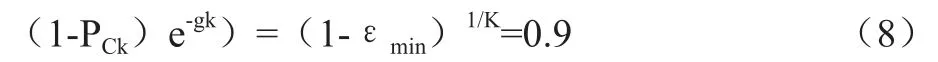
对于f（x）=e-x，当f（x）的值接近于1时，x≈1-f（x）。因此PCk和gk有如下关系：

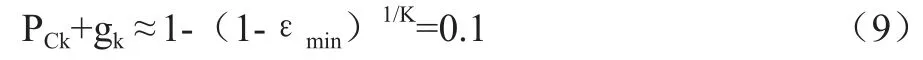
本文提出迭代优化算法。当K值确定时，只要PCk、gk中有一个变量的值确定后，另一变量的值也随之确定。因此在Pk/gk取不同值时，可以计算对应功率的最优值，而后依据Pi的规律采用二分法搜索得到最优的Pk/gk。

3 真实验结果分析

图2为在不同QoS参量θ取值（λa=2000packets/s，distance=100m）、不同数据包速率λa取值（theta=1，distance=300m）、不同通信距离（theta=1，λa=2000packets/s）的情况下，重复传输次数与传输功率消耗的关系。

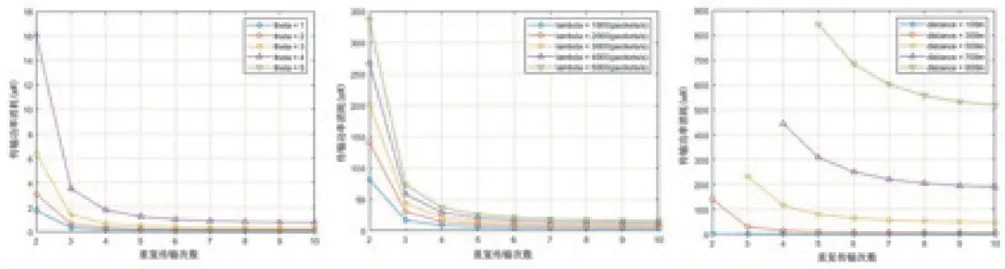
图2 不同情况下重复传输次数与传输功率消耗的关系

如图2所示，仿真实验结果表明，随着重复传输次数的增加，无论θ取值为何值，系统的传输功率都呈下降趋势。但当θ取值增加到5时，此时系统无解，这是由于系统带宽有限造成的。在不同的数据包达到过程下，系统的传输功率消耗差别较大，但当传输次数增加到一定值之后，不同数据包达到过程之间的传输功率消耗的差别变小了许多，表明重复传输对系统可靠性的提高效果是显著的。当用户的通信距离达到一个值时，仅通过有限次的重复传输并不能实现URLLC的可靠性要求，这时只有继续增加重复传输次数，才有可能实现URLLC的可靠性要求。

4 结束语

本文研究了URLLC通信中超高可靠性的实现，提出最小化重复传输功率模型。尽管文中提出的最优化问题无法直接求解，但由于K值的取值范围较窄，因此可以针对K的每一取值分别求解。在给定K值的情况下，提出并利用迭代优化算法对问题进行求解。仿真结果显示，虽然单次传输不能满足系统的可靠性要求，但在信道质量较好以及数据包速率较低时，仅增加一次重复传输，URLLC中的可靠性要求即可实现，且总的传输功耗也有所降低，而且当重复传输次数达到一定值之后，重复传输所带来的功率消耗基本保持不变。