非结构环境下一种改进的区域生长点云分割方法
2021-10-15刘克平
刘 玮, 李 岩, 贾 科, 刘克平*
(1.长春工业大学电气与电子工程学院, 长春 130012; 2.长春一汽国际物流有限公司, 长春 130000)
近年来,点云处理技术逐渐应用在非结构环境下的目标零件识别领域[1]。非结构环境,即环境信息未知、不固定,且存在零件杂乱摆放相互堆叠、连接的情况。如何将单个零件从复杂背景中准确地分割出来,依旧是点云处理过程中待解决的难题。点云分割结果的好坏,将直接影响后续目标识别的精确度[2]。
目前,常用的点云分割方法有:基于聚类的分割、基于区域的分割、基于边缘的分割以及基于模型的分割。第一类是基于聚类的分割方法。Wang等[3]提出了一种基于距离的聚类方法来解决物体重叠放置的问题,根据高斯映射的特性和点的几何信息,可以识别出平面、圆柱体、球体等原始形状,从而避免了点云的过分割。Sansoni等[4]提出了一种对欧式聚类进行优化的算法,用于识别有噪声和遮挡情况下自由形状的物体,使用定制开发的分割算法集成商业软件库并通过相同扫描系统创建的模型云数据库来执行对象识别。上述方法在处理点云分割问题时,仅限于识别固定形状的物体,在解决其他场景问题时具有一定的局限性。第二类是基于区域的分割方法。杨琳等[5]提出了一种结合超体素和区域生长的点云分割算法,首先获得点云的空间位置信息,其次利用超体素的中心合并成均匀分布的点云,再依据其点云特征得到点云子集,最终进行区域生长聚类。Bab等[6]在传统区域生长算法的基础上进行相关改进。首先,为了解决模型选择问题,引入了一种基于最小化拟合曲面应变能力的新准则。根据该准则,提出了一种稳健的数据分割算法用于分割复杂的平面与曲面对象。上述方法在进行区域生长过程中,对于初始种子点位置的选取要求较高,并且容易受到噪声点的影响。第三类方法是基于边缘的分割,Bao等[7]提出了一种基于三维点云的边缘检测方法,所采用的是Canny算子提取二维图像中的边缘,再根据映射算法得到三维数据的边缘点。王宗跃等[8]使用少量时间对点云数据进行网格划分,对非边缘网格进行快速去除,节省了Alpha Shapes做条件判断的时间。但上述方法仅适用于密度较小的点云数据,不具有普遍性。第四类方法是基于模型的分割。朱军桃等[9]提出一种将三角面作为基元,并搭建Delaunay三角网格的连接关系,对区域生长算法进行简化,解决了屋顶交界处存在采样点异常的问题。Chen等[10]为了提取每个基元边界,引入了一种新的基于Voronoi图的建筑物内外边界约束下的基元边界提取算法。上述算法对于处理建筑物以外的物体,效果不佳,极易出现过分割或欠分割的情况。
根据环境中存在零件无序摆放的情况,选择基于区域的分割算法进行点云分割。在传统区域生长中通常采用随机抽样一致性算法获取初始种子点,但该方法只有一定概率能够获得可信的模型,容易出现分割不稳定的现象[11]。因此,针对传统算法的不足进行改进,通过计算点云曲率,将曲率最小点设置为初始种子点,再根据位置信息设定空间阈值范围进行区域生长,提高了点云分割的稳定性和准确性,同时兼顾了分割效率,为后续的目标识别过程奠定基础。
1 算法原理
非结构环境下,改进的区域生长点云分割方法主要流程包括:点云预处理、建立点云拓扑关系以及改进区域生长算法,如图1所示。
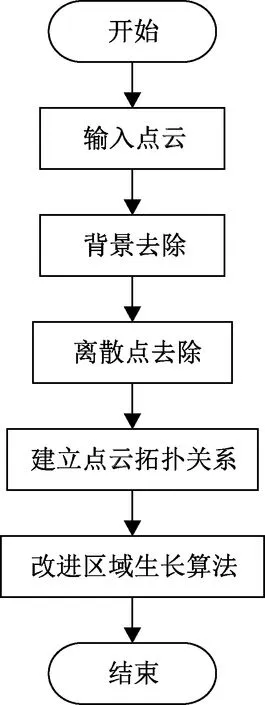
图1 改进的区域生长点云分割算法流程图Fig.1 A flow chart of the improved segmentation algorithm for regional growing point cloud
1.1 数据获取
使用视觉测量装置CCD(charge-coupled device)工业相机、一台DLP(digital light procession)投影仪来获得点云数据,但采集点云数据时会受到周围复杂环境的影响,容易出现大量的冗余点、离散点且会出现点云密度过大的现象。其中,冗余点来自周围的多余背景,属于非感兴趣区域;离散点是指远离感兴趣区域的点,来源于未完全去除的冗余点和实际拍摄中存在的误差点,其点云密度远小于感兴趣区域。这二者均会对点云数据的后期处理速度和效率造成一定影响。因此,需要对采集的冗余数据进行合理的精简,加快后期数据的计算速度。
点云预处理步骤如下。
(1)采用直通滤波器对多余的背景信息进行去除。
(2)采用基于平面模型的分割方法对采集的平面进行去除。
(3)使用Statistical Outlier Removal滤波器来剔除离群点或拍摄导致的误差点。
通过以上点云预处理过程进行噪声去除,以图2(b)初始点云(共661 522个点)为例进行实验,图2(f)为预处理完成后的点云(共113 708个点)。点云精简率高达82.8%,实验结果如图2所示。由此可见,该预处理过程能够有效去除冗余点及离散点。

图2 预处理示意图Fig.2 Preprocessing schematic
1.2 建立点云拓扑关系
在进行点云预处理过程之后,数据通常还会存在无规则分布的情况[12]。因此,在对点云进行分割之前,需要建立点云之间的拓扑关系,加快邻近点的搜索,提高点云分割的效率。采用八叉树建立点云之间的拓扑关系,八叉树(Octree)即一种自上而下、逐级划分的三维空间树状结构[13-14],该层级结构如图3所示。首先选取任意一个空间作为根节点,如果需要把空间进行细分时,将该节点划分为八个子节点。当其中某个子节点需要继续划分时,则持续划分为八个子节点,再将图中所示的根节点与子节点相互连接,该树状结构称为八叉树。空间结构如图4所示,空间递归划分,建立点云之间的拓扑关系如以下步骤。
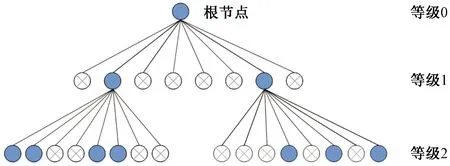
图3 八叉树层级结构图Fig.3 Octree hierarchy diagram
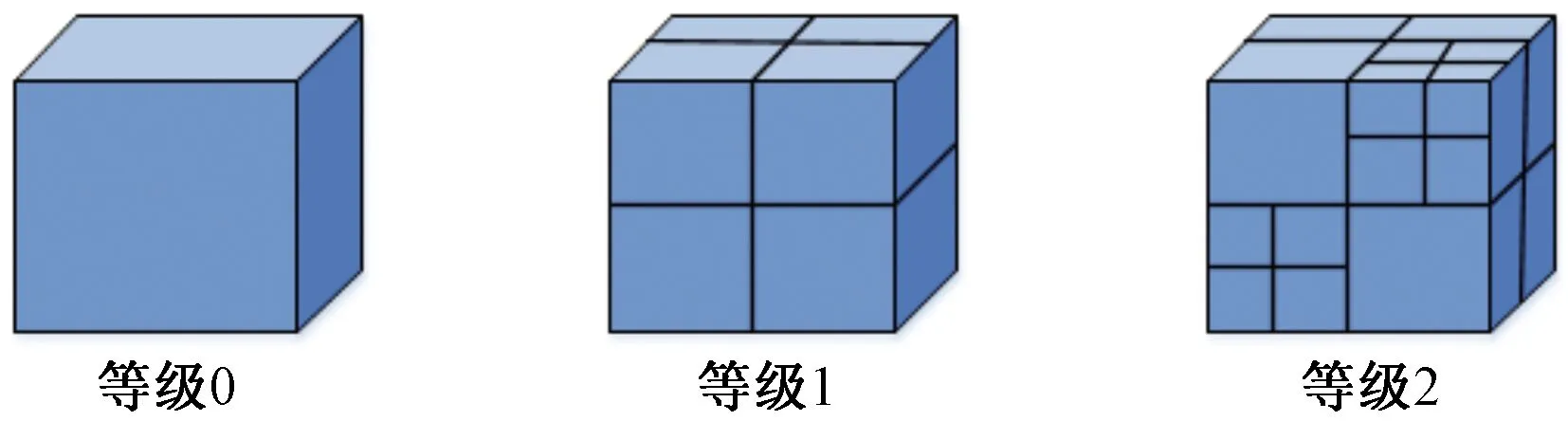
图4 八叉树空间结构图Fig.4 Octree space structure diagram
(1)首先,依据点云数据模型的最小空间包围盒确立八叉树根节点。
(2)其次,将八叉树的根节点分别沿X、Y、Z轴方向采取均等划分,将立方体逐步等分为8个小立方体,每个小立方体即为根节点的子节点。
(3)最后,对所有根节点以及子节点进行递归划分,直到小立方体边长满足所设置的阈值时停止划分。
通过以上步骤能够对点云进行区域划分,为后续的点云分割提供了便利。
1.3 改进区域生长算法
在完成点云拓扑关系建立后,使用区域生长算法进行点云分割。首先,设定有效的生长准则。其次,选定某一个数据点作为生长的初始种子点,将点集中具有相似几何特征的数据点划分到一个区域,再判断该区域中邻近点的选取是否符合设定的生长准则。最终,在所有满足阈值条件的邻近点都加入到种子区域后,停止生长。
该算法的分割结果在很大程度上取决于初始种子点的选取。当前,传统区域生长算法在进行点云分割时通常采用RANSAC(random sample consensus)算法[15]获取初始种子点,但容易出现分割不稳定的现象。为了克服该缺陷,提出一种改进的区域生长算法来进行点云分割。该算法用于解决重叠分割问题,通过减少区段总数,从而提高点云分割效率。将曲率最小点设置为初始种子点,即选择所在平面最平滑的部分开始生长。
在进行点云曲率计算时,常见的方法有主成分分析(principal component analysis,PCA)法以及最小二乘法等。由于PCA方法对点云曲率的计算较为粗略,而最小二乘法计算曲率较为烦琐。综上考虑,选取一种基于局部径向基函数(radical basis function,RBF)的点云曲率计算方法,构建完整的隐式曲面,再根据曲率的微分几何性质来进行计算。基于RBF构建的隐式曲面光滑性、延续性较好,且该方法稳定性高,鲁棒性强。
首先,将所获得点云的采样点定义为pi,将其k邻域定义为Nk(pi),使用1.2节的方法对k邻域进行加速搜寻。根据反复试验,k会有相应的取值范围。选择差异较大的k进行对比:当k较小时,所构造的局部曲面拟合程度较小;当k较大时,局部曲面拟合程度较大。其次,定义某一平面区域的n个目标点为{p1,p2,…,pi,…,pn},且分别对应的约束值为{h1,h2,…,hi,…,hn}。需要构造一个隐式曲面来计算点云的曲率,即构造函数f(r)中各目标点均符合方程f(pi)=hi,则方程f(pi)=0就满足构造的隐式曲面,该方程为
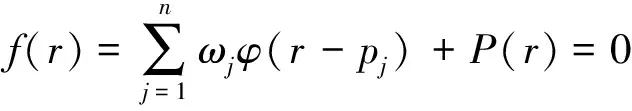
(1)
式(1)中:r为插值约束点,即构造隐式曲面的随意杂乱点;pj为构造隐式曲面时的目标点;ωj为对应目标点的径向基权值;P(r)即一次多项式,对随机一点(x,y,z),P(r)=a0+a1x+a2y+a3z;φ(r-pj)为径向基函数,通常的表示方式为φ(x)=|x|3。
由给定的n个散乱点确定约束条件为
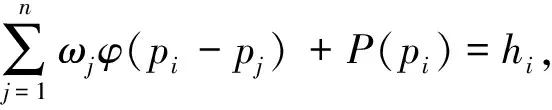
i=1,2,…,n
(2)
其次,使式(2)取得最小值需要符合的正交关系为
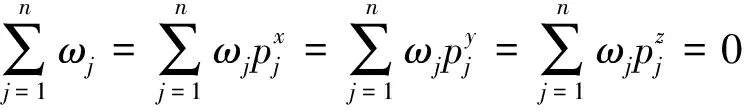
(3)
由式(2)、式(3)可以构建线性方程组为

(4)
对式(4)进行求解,获得仅有的一组解(ω1,ω2,…,ωn,a0,a1,a2,a3)。将求得的解代入式(1)中,得到该隐式曲面方程为
f(x,y,z)=
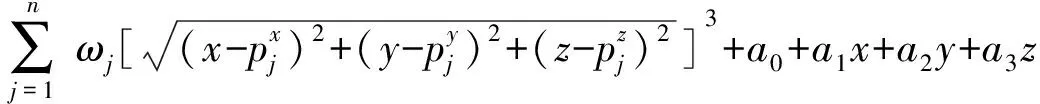
(5)
由隐式曲面的曲率性质计算其曲率,并将其近似为目标点的曲率值。并从中选择曲率最小的点进行生长。对需要进行分割每个点的曲率进行计算并排序,隐式曲面任一点Q的曲率K为
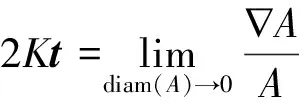
(6)
式(6)中:t为法向量;A为Q点周边无穷小的区域,即隐式曲面f(x,y,z)所代表的区域;diam(A)表示为该区域直径;∇为点Q的梯度算子。将式(6)离散化,得到Qi的曲率为
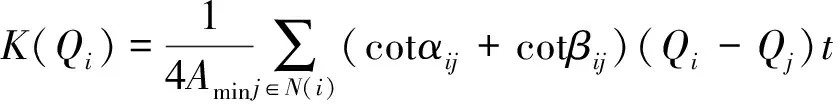
(7)
式(7)中:αij、βij分别为连接Qi和Qj边的对角。经过迭代计算,求取出点云曲率的最小值。
改进区域生长算法的具体步骤如下。
(1)首先对每个点的曲率进行计算,再依据大小值排列顺序,选择曲率最小点为初始种子点进行生长。
(2)其次,通过设定候选的种子点集合P、聚类区域Q以及空间阈值,进行邻近点搜索判断。如果生长半径以及垂直距离满足阈值条件,则将该点转移至聚类区域Q。
(3)再将拟合曲面与种子面法矢量进行对比,如果两夹角满足阈值范围,则将该点添加至种子点集合P中。
(4)删除当前种子点,利用新加入的种子点继续生长,循环执行步骤(2)和(3),直到种子集合为空。
2 实验与分析
2.1 实验平台设计
为了验证该分割方法的有效性,选择视觉测量装置(一个CCD工业相机、一台DLP投影仪)作为点云数据采集设备,相机到工件的距离为 1.1 m。视觉测量装置垂直位于工作台上方,零件随机摆放在工作台上,如图5所示。在本实验平台下,进行了两个场景的实验,场景一所选取的零件为金属盘型元件以及塑料三通管,场景二所选取的零件为金属盘型元件、塑料三通管以及汽车金属件。分别使用DBSCAN(density-based spatial clustering of applications with noise)聚类算法、传统区域生长分割算法以及本文算法对场景中的无序点云进行分割。本实验采用PC(personal computer)机安装64位的Windows 10操作系统,配置为Intel Core i5-9500CPU、3.0 GHz、16 GB内存,使用的汇编语言为C++,应用平台为64位的VS2017,开发环境为点云库PCL1.8.1。

图5 实验平台装置图Fig.5 Device diagram of experimental platform

数字表示点云子集图6 三种算法不同场景下分割结果图Fig.6 Segmentation results of the three algorithms in different scenes
2.2 对比实验
区域生长算法的原理是将符合约束条件并具有类似特征的点聚在一起。因此,分割的结果为一系列点云子集,具有相同颜色的点云子集表示为一类。图6中对场景一和场景二,分别使用DBSCAN聚类算法、传统区域生长算法以及改进的区域生长算法,对完成预处理以及拓扑结构建立的点云数据进行分割。
在给定目标子集个数相同的情况下,分别记录三种算法分割出的子集个数、正确分割的子集个数。如表1所示。
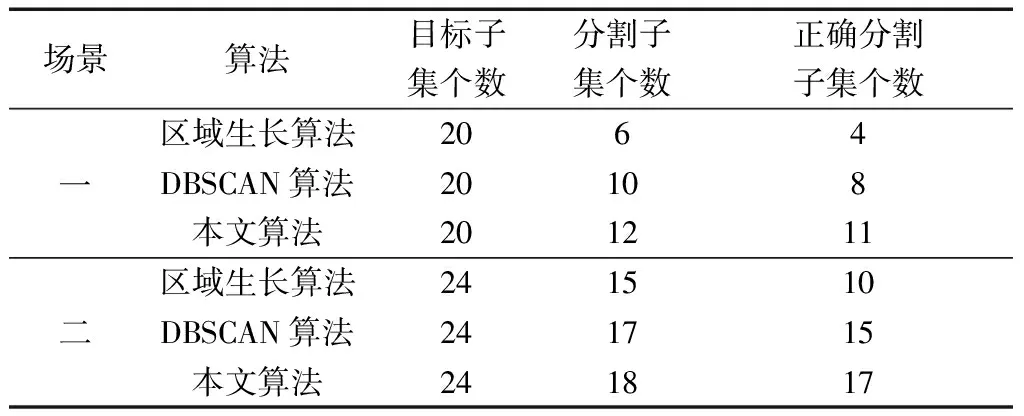
表1 三种算法分割效果对比表
其次,为了评估算法的效果,采用以下定量指标进行分析:分割正确率Rs以及算法耗时,用于本文算法的性能分析。在理想分割中,属于一个类别的点将在同一点云子集中,但由于噪声和其他环境因素影响,一些点集没有被正确分割。
第一个评价指标Rs,即分割正确率计算公式为
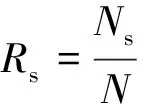
(8)
式(8)中:Ns为正确分割的点云子集个数;N为分割子集个数。
第二个评价指标为算法耗时,通过记录各算法运行时间表示该指标。如表2所示。
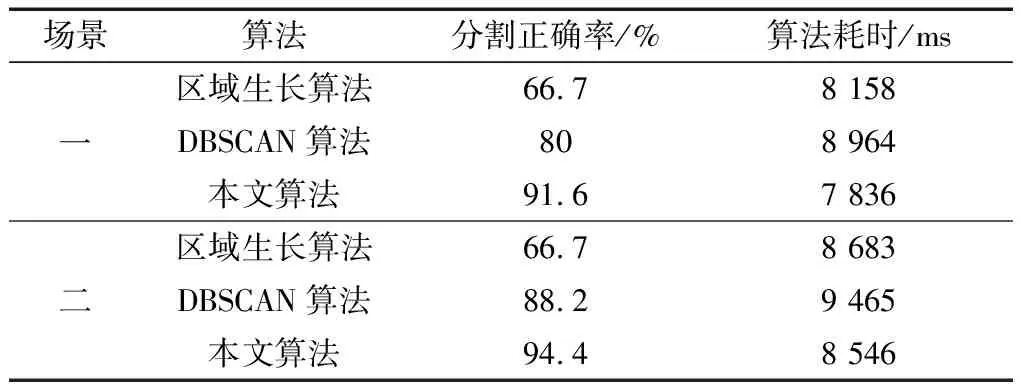
表2 三种算法分割效果对比表
2.3 实验结果分析
(1)在目标零件个数相同的情况下,相比于传统的区域生长算法,本文算法能更加准确地分割出目标零件子集。表1中对场景一的结果进行显示,传统区域生长算法共分割出6个点云子集,其中4个点云子集为正确的子集,出现了欠分割现象。而本文算法共分割出12个子集,其中11个为正确分割子集,未出现明显的欠分割现象。本文相较于传统区域生长算法,分割正确率提高了24.9%。
(2)相比于DBSCAN聚类算法,本文算法具有更快的分割效率,算法耗时更短。从表2中场景一可以看出,本文算法耗时相较于DBSCAN聚类算法,速度提高了12.5%。
3 结论
提出了一种非结构环境下改进区域生长的点云分割方法,用来解决点云分割中零件相互堆叠的情况。首先,采用直通滤波和统计滤波的方法进行离散点以及冗余点的去除,方便后续数据的处理;其次,使用八叉树建立点云之间的拓扑结构,提高点云分割的效率;最后,通过改进的区域生长算法,选择基于局部径向基函数的曲率计算方法,选取曲率最小点为初始种子点,并设定空间阈值范围进行区域生长。由此提高了无序环境下点云分割的正确性和效率。实验结果表明,本文提出的算法对于相互堆叠的零件点云,分割正确率提高了24.9%,速度提高了12.5%。
